铂晶体位错的结构能量和电子性质的研究

于 帆， 王 磊， 孙建平

（1.北京科技大学能源与环境工程学院，北京100083； 2.中国航天空气动力技术研究院，北京100074；3.中国计量科学研究院，北京100029）

高纯度铂丝材料作为标准铂电阻温度计的感温元件，其物理化学性质对于标准铂电阻温度计的精准性有着极其重要的影响［1-3］.位错作为材料中常见的缺陷之一［4-5］，其数量和分布状况对材料的力学性能、化学性能及光电特性有重要影响.传统的实验方法只能观察位错线的分布和运动，而不能观察位错核心区的原子分布，借助于分子动力学（MD）模拟［6-7］以及第一性原理计算［8-12］可以实现这一目标.Clouet［13］通过MD方法模拟面心立方金属中的位错，并与弹性理论进行了比较.Gehlen等［14］探讨了边界条件和势的不同对位错芯计算的影响，并给出了铁位错芯的半径.Soleymani等［15］采用4种嵌入原子法（EAM）势函数来再现铝中边缘位错周围的应力场，发现在位错周围再现应力场的能力并不是最好的.牛原等［16］用Dmol团簇法计算了Fe中刃型位错的电子结构，发现位错芯区具有捕获杂质的作用.文献［17-18］分别用分子动力学方法模拟了位错对铜体积的影响和位错环的反应.

综上来看，借助于分子动力学和第一性原理研究材料位错的方法已经相当成熟，但是对研究铂晶体位错的文献却很少有报道.因此，本文利用MD方法和第一性原理，对铂晶体中的刃性位错的结构能量和电子结构进行系统的研究.

1 计算模型和方法

1.1 分子动力学模拟使用大规模原子分子并行模拟器（LAMMPS）建立位错模型［19］.采用在模拟金属材料中常用的嵌入原子法（EAM）做为势函数［20-21］.由于铂晶体属于面心立方晶体，其滑移面为（111）面，滑移方向为＜110＞方向，柏氏矢量为取晶体3个晶轴方向分别为x、y、z轴建立刃型位错模型.模型的尺寸为40a×20a×50a（a＝0.392 4 nm），共79 640个原子，如图1所示.

在模型的基础上，对此结构进行弛豫，经过多次迭代，得到了稳定的位错结构.如图2（a）所示，取位错中心区的原子在y轴的投影，实际边长为1.0，建立坐标点.如图2（b）所示.

图1 弛豫前位错的原子结构Fig.1 The atoms configuration of a dislocation before relaxation

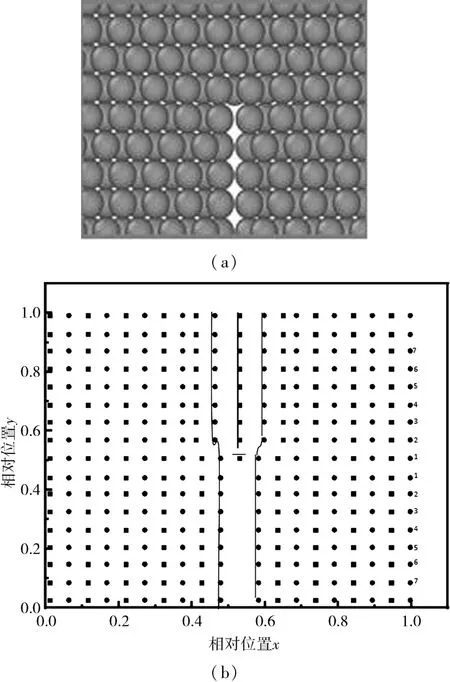
图2 （a）弛豫后位错的原子结构（b）弛豫后位错的原子结构位置的投影Fig.2 （a）The atoms configuration of a dislocation after relaxation；（b）Projection of the atoms configuration of a dislocation after relaxation

详细的坐标分析表明，弛豫后刃型位错具有C2V点群对称性.

1.2 位错应变能的计算由于模型缺失了半个原子面，导致在滑移面附近的原子离开原来的平衡位置发生点阵的畸变，滑移面附近的原子能量升高.由此升高的能量就是位错应变能，它由两部分组成，一部分是位错核心区由于原子位置严重的错排所增加的能量，即位错畸变能Ecore，另一部分是核心区以外，由于位错而导致原子的微小位移所引起的弹性应变能Ee.弹性应变能Ee可以通过连续介质弹性理论计算得到，但是却无法准确地计算出畸变能Ecore［24］.为此，通过分子动力学模拟可以计算出弛豫后位错核心区原子的格位能.图3（a）和图3（b）分别表示位错中心区域滑移面上4排原子和下7排原子的能量分布.

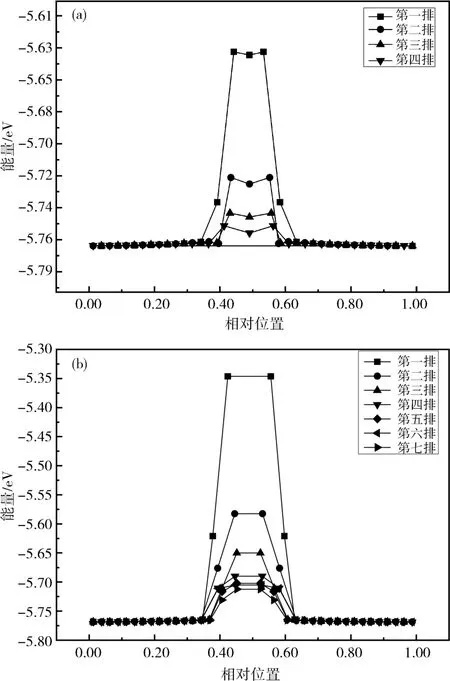
图3 （a）滑移面上方4排原子的能量（b）滑移面下方7排原子的能量Fig.3 （a）The energy of the 4 rows of atoms above the glide plane（b）The energy of 7 rows of atoms below the glide plane

从图3可以看出，滑移面以上和滑移面以下的原子能量关于位错线对称.滑移面以上的第一排原子能量变化比其他几排原子的能量变化大，滑移面以上第一排原子的最高能量为-5.635 eV，比完整晶体中原子的能量E0＝-5.769 eV高0.134 eV.如图3（b）所示，滑移面以下的靠近位错线的原子能量变化要比位错线上方的大，说明在滑移区原子能量变化比未发生滑移的原子能量变化大.滑移面下第一排的最高原子能量为-5.345 eV，比完整晶体中原子的能量高0.424 eV.滑移面下第二排原子的最高能量为-5.182 eV，比完整晶体中原子的能量高0.587 eV.我们认为由于滑移面下第二排原子的滑移程度比滑移面下第一排滑移程度大，所以能量更高，更不稳定.在图3中能够很好看出滑移面下第三排之后的原子的最高能量趋于稳定，比完整晶体中的原子能量高0.587 eV左右.

计算刃型位错的位错应变能和畸变能以及位错芯区半径.刃型位错的能量可以表示为：

其中，K是仅依赖于位错构型和材料弹性性质的一个常量（μ为剪切模量，ν为泊松比），b为位错柏氏矢量的模，R为位错应力场的作用半径，rc为位错芯半径.位错区内每个原子对位错应变能的贡献为Wi-W0，则总的位错应变能为：

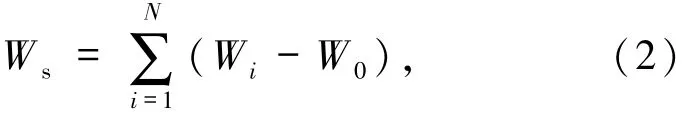
其中，Wi为弛豫后第i个原子的能量，W0为完整晶体中每个原子的能量，N表示以位错线为轴线半径R的圆柱体内的原子个数.由（2）式计算可得表1.

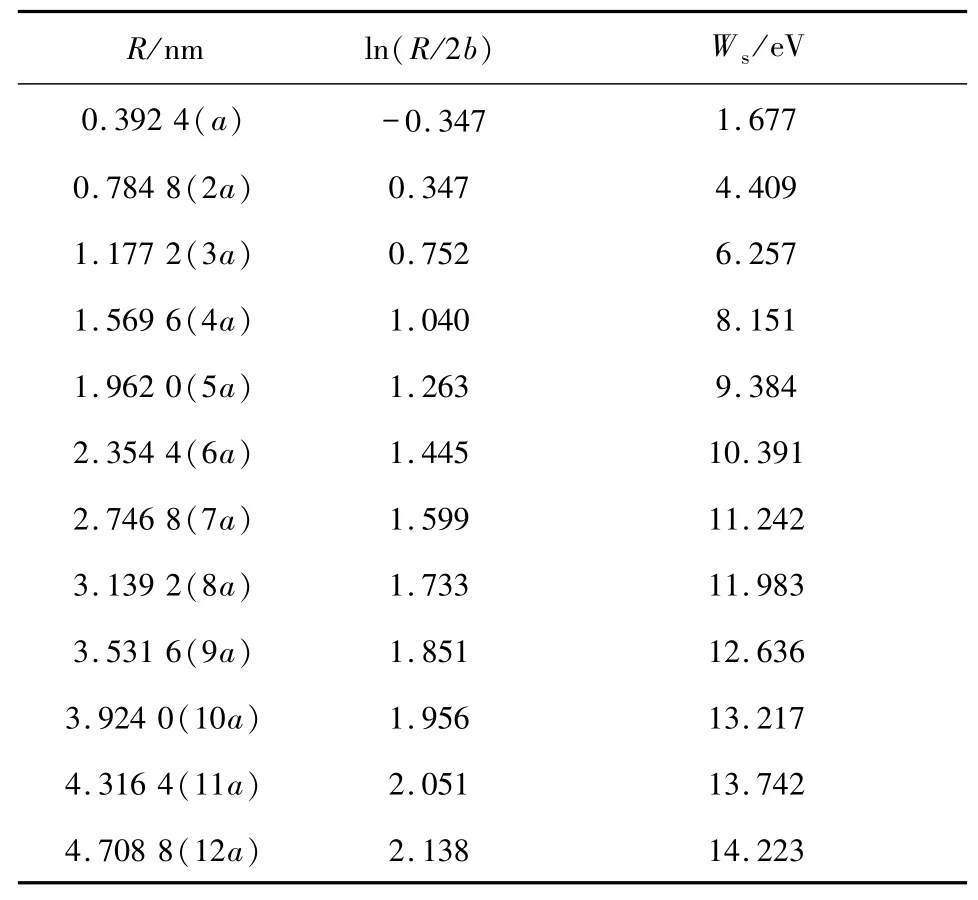
表1 刃型位错中对应不同R的应变能WsTab.1 Strain energy Ws corresponding to different R in edge dislocations

通过做W-ln（R／2b）图（见图4），可以计算出位错芯半径rc和畸变能Wcore.

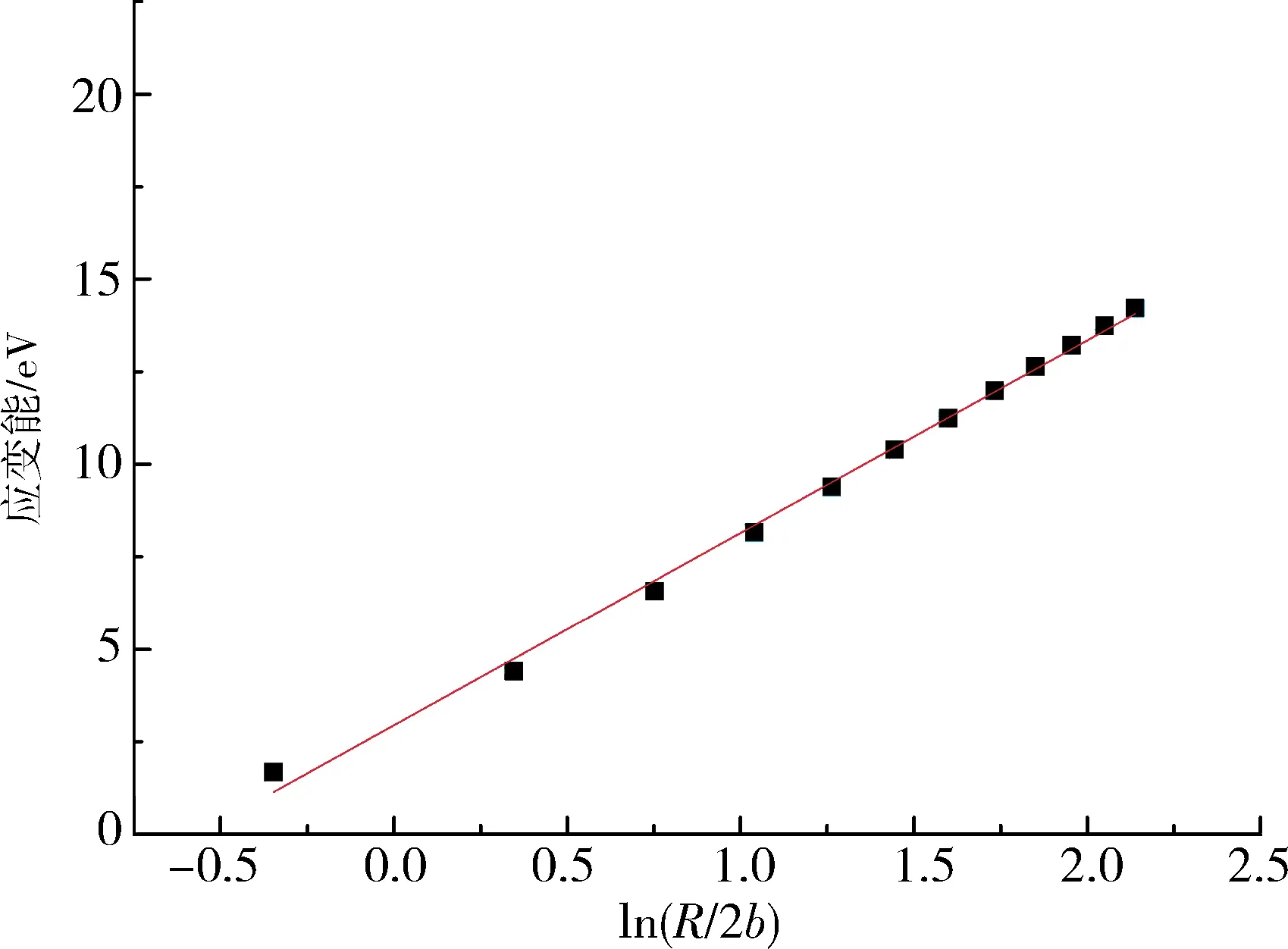
图4 位错应变能Ws与力场作用半径R的关系Fig.4 Relationship between dislocation strain energy Ws and force radius R

从图4中可以看出，当ln（R／2b）＞0.347时，W-ln（R／2b）成线性关系.通过拟合得到Wcore＝2.400 eV，K＝7.182 eV（接近弹性理论计算结果K＝7.192 eV），位错芯半径rc＝2b，位错芯半径为0.554 9 nm.

1.3 态密度计算和分析采用CASTEP软件包计算由刃型位错导致滑移部分原子的电子结构.模型选取了滑移面附近的344个原子.采用超软赝势和PBE泛函对结构进行几何优化并计算电子结构.

采用的收敛标准为截断能，设定为250 eV，k点取为2×3×1，能量为1.0×10-5eV／原子，受力判据为0.03 eV／0.1 nm.采用BFGS算法对结构进行优化.计算刃型位错滑移面上下5排原子的电子结构和态密度，结果如图5所示.

图5（a）是滑移面上方5排多余半个原子面的原子的总态密度，图5（b）为滑移面下5排紧邻位错区原子的总态密度，图5（c）为滑移面上5排多余半个原子面原子的d带态密度，图5（d）为滑移面下5排紧邻位错区原子的d态密度，图5（e）为滑移面上5排多余半个原子面的原子的s态密度，图5（f）为滑移面下5排近邻位错区原子的s态密度.

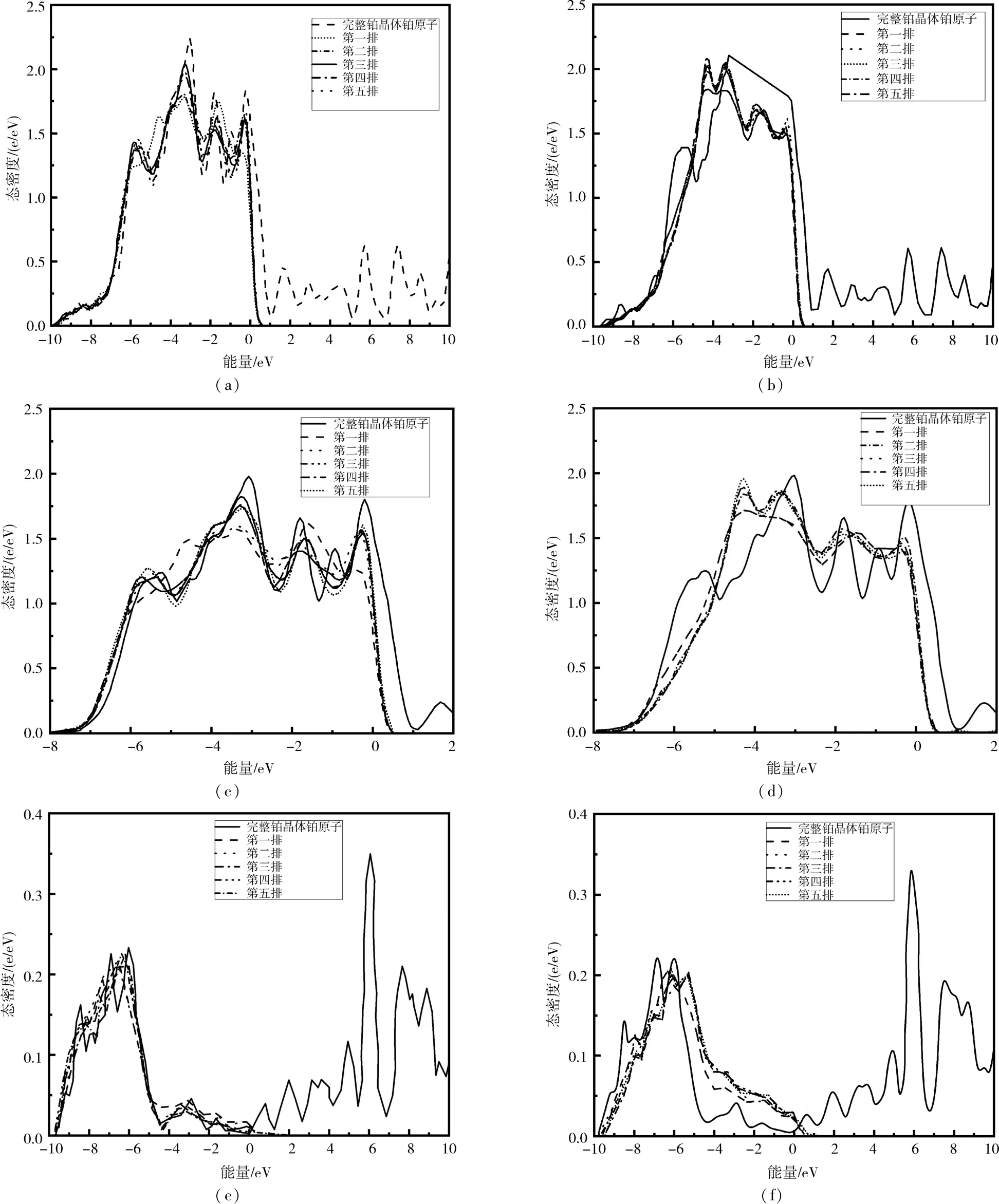
图5 计算的位错周围铂原子的态密度Fig.5 The calculated DOS about Pt atoms around the dislocation

比较完整晶体中的铂原子和位错核心区周围的原子，可以获得不同原子和部分轨道之间的电荷转移，便于分析原子间相互作用和原子间键合特性.发生位错之后，位错核心区周围的原子电子结构变化很大.滑移面上方的原子比滑移面下方原子态密度的变化小.滑移面上方原子的总态密度相较于完整晶体中铂原子的总态密度而言，带峰减少，远离位错核心原子的电子占据数与完整晶体中原子电子占据数相近.但是，在费米面处随着原子位置远离位错核心，其态密度增加；滑移面下方的原子相较于完整晶体中铂原子的总态密度而言，带峰左移，随着原子远离位错核心，其带峰的高度增加，在费米面处，滑移面下方总态密度低于完整晶体中铂原子的总态密度，但是原子与位错核心间距离的改变却没有很明显地改变费米面处的电子态密度.无论原子位于滑移面上方还是下方，其d带态密度变化和总态密度变化趋势一致，但是，其s带态密度与完整晶体中原子的s带态密度变化差距较大.原子位于滑移面上方，其s带态密度带峰的高度接近于完整晶体中铂原子的s带态密度，带峰左移，在费米面处略高于完整晶体中铂原子的态密度.而原子位于滑移面下方，其s带态密度带峰右移，较明显地低于完整晶体中铂原子s带态密度，在费米面处的s带态密度明显高于完整晶体中原子的s带态密度.而位错核心附近的原子s带态密度在费米面右侧，均明显小于完整晶体中铂原子s带态密度.

通过对比分析，发现计算出的电子结构最显著的特征是能量范围的缩小，可以用经典的最近邻断裂概念来解释.完全晶体中的每个铂原子都有12个最近邻，而在位错模型中只有8个最近邻，导致了局部态密度（PDOS）的进一步变化.态密度的改变反映了电子结构的变化，这是造成位错不稳定的原因.

2 结论

利用分子动力学和第一性原理的计算方法得到铂（Pt）中＜110＞（111）刃型位错的结构、应变能、位错芯能量和位错芯半径及其位错中心区原子的电子结构.

1）通过应变能的计算，发现铂（Pt）中＜110＞（111）刃型位错中心区原子能量具有对称性，原子坐标具有C2V点群对称性，这和文献［22］相一致.

2）计算原子的格位能，通过格位能的分析得到了位错芯能量为2.400 eV，位错芯半径为0.554 9 nm，K＝7.082 eV，接近弹性理论计算结果（K＝7.192 eV）；格位能的计算表明发生滑移原子的能量比未发生滑移原子的能量高.

3）态密度的计算表明，位错会导致位错中心区原子的电子结构发生较大变化，电子结构的能量范围减小，这是造成位错不稳定的原因.