拨动扩散思维之弦 探究数学奇幻之美——对初中数学中“多做少想”现象的思考

■郝云凤

当前的初中数学教学存在着学生做题目的时间多，想题目的时间少这样的问题。换言之，就是学生只是在埋头做题，没有真正地去思考与题目相关的一系列问题。这样的模式会导致学生做了许多题目，却不知道题目的内核是什么，在遇到新的题目的时候，不能从做过的题目中汲取方法与思路。因此，教师要加强解题教学中的过程性引导，帮助学生的思维品质在一题多想的过程中得到改善，在学习上达到事半功倍的效果。提升思维的逻辑性，思考题目之间的联系；提升思维的广阔性，思考更多的思路；提升思维的深刻性，思考问题的内核是什么；提升思维的独立性，思考这道题目的不同之处在哪儿；提升思维的灵活性，思考有没有更多的解法；提升思维的敏捷性，思考有没有更简单、更快捷的方法；提升思维的批判性，思考别人做题的优点与不足。

一、培养学生的生活意识

数学与生活总是有一定联系的，在生活中随处可见数学的影子，在数学原理与公式中也能发现生活中的例子。在数学教学中，要让学生将题目与生活联系起来，从而让他们的思维得到转化，将抽象思维转化为形象思维。因此，在学生遇到某一题目时，要让他们多想一想生活中有没有相似的情境。当学生能将题目融入生活，他们就会对题目多一份亲切感，少一份生疏感，进而更容易想出解决的路径。学生将题目和生活联系起来，在某种意义上也说明他们看懂了题目。

以实际问题与一元一次方程等相关问题为例，笔者设置了这样一道题：某地的A、B两家工厂急需煤90吨和60吨，该地的C、D两家煤场分别有100吨、50吨，全部调配到A、B两家工厂，已知C、D两个煤场运到A、B两家工厂的运费（元/吨）如下表所示：

目的地出发地A B C D 35 40 30 45

运送完毕后，A、B两家工厂共付运费5200元，问煤场C、D各有多少吨煤运往A工厂。对于这样的题目，学生很快就能想出解题的思路。他们先设C运给A厂x吨，那么C运给B厂就是（100-x）吨，D运给A厂就是（90-x）吨，D运给B厂就是（x-40）吨。同时他们由题意得出35x+40（90-x）+30（100-x）+45（x-40）=5200，进而求得x=40，所以煤场C、D有40吨和50吨煤运往A工厂。

解答完这样的题目，学生就在想：这不就是用数学来解决生活中的问题吗？生活中像这样的例子不是还有很多吗？教师再引导学生想一想生活中有没有数学的影子，其实就是通过生活实际将数学中的认知以更直观的方式展示出来，这也是解决数学问题的一种有效方式。

二、培养学生的问题意识

在预习的过程中，教师问什么问题学生就思考什么问题，将相关的问题弄懂，预习也就结束；在互学的过程中，教师会抛给学生一些问题，他们会围绕问题展开讨论，以得出一些结论；在展学的过程中，教师会设置一些问题，让学生将认知转化为解题的能力，提升素养。明显地，在这种模式下，教师成为课堂的主体，掌控着整个课堂的节奏，学生只是在被动地接受。在数学教学的过程中，让学生去发现问题，比解决问题更重要。学生去发现问题，首先，要有一定的识记能力，要能记得相关的原理与定律；其次，需要一定的推理能力，即由这些定律会发现题目中存在的问题；最后，还要有一定的分析能力，即要分析这些问题是否真的成立，并找到解决方案。因此，在解答一道题之后，教师可以让学生的思维保持继续发展的态势，让他们想一想有没有新的问题。

在学习等边三角形的相关知识时，笔者设置了这样一道题：点A是线段BC上一点，△ABD、△AEC都是等边三角形，BE交AD于点M，CD交AE于点N，如图1所示。求证：BE＝DC。

图1

对于这样的问题，学生很快就能想到，因为△ABD、△AEC都是等边三角形，所以AD=AB，AC=AE，∠DAB=∠CAE=60°。有了这些结论，他们就能通过列举条件，进而证得△DAC≌△BAE（SAS），所以就有了BE＝DC。之后，笔者引导学生继续观察图形，发现题目中给出的条件能得出更多的结论。他们试着证明△AMN是等边三角形，先是利用△DAC≌△BAE这一结论，得出∠ABM=∠ADN；再从已知条件推出的∠BAD=∠EAC=60°中得出∠DAN=60°；然后又由AB=AD，得出了△ABM≌△ADN（ASA），进而有AM=AN，同时又因为∠MAN=60°，证得△AMN是等边三角形。

学生充分利用条件和新结论的过程，就是他们思维向纵深发展的过程。让学生多想问题，一方面教师能更直观地看出学生思维的特点，再为他们制定更好的教学方案；另一方面学生能更主动地投入到课堂中来，成为课堂的设计者，而不仅仅是一个听众。

三、培养学生的关联意识

在教学的过程中，我们经常会遇到这样一种情况，一道题讲了很多遍，学生在做题的时候还是会出错。可是在这些做错的学生当中，有许多在听讲的时候，是明白做题思路的。可为什么换道相似的题，他们就出问题了呢？这其中一个主要的原因就是学生在做题的过程中缺少思考的过程，即没有去思考有没有做过相似的题。他们没有从做过的题目中找寻经验和灵感，将相关认知联系起来。

每道题的出现都不是孤立存在的，从做过的题目入手，能更快地唤醒曾经的思路，找到解题方法。例如下面这道题。如图2，已知AB是⊙O的直径，AC是⊙O的切线，连接OC交⊙O于点D，连接BD。若∠C＝40°，则∠B=_____。

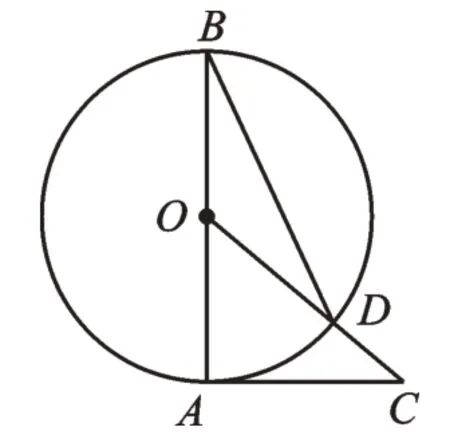
图2

按照通常的思路，教师会问：因为AC是⊙O的切线，所以我们能得出什么结论呢？学生会答：OA⊥AC，∠OAC＝90°，∠AOC＝90°-∠C＝90°-40°＝50°。教师再问：因为OB＝OD，又能得出什么结论呢？学生答：∠OBD＝∠ODB。同时他们还会补充说，因为∠AOC＝∠OBD+∠ODB，所以∠OBD=∠AOC＝25°，即∠ABD的度数为25°。这样的教学模式，只是就题论题，学生的思维没有往更广阔的领域发展。教师可以引导学生将以往做过的题目联系起来，既触类旁通，又彼此补充，不断深化。

学生翻看各种讲义，他们发现这样一题：如图3，AD是⊙O的弦，AB经过圆心O，交⊙O于点C，∠DAB=∠B=30°，问直线BD与OD形成的角是否为90°。学生发现此题同样是运用有关切线的认知求某一角的数值，在解决过程中同样需要将角度之间的数值进行转换。连接OD，由∠ODA=∠DAB=∠B=30°，得∠ODB=180°-∠ODA-∠DAB-∠B=180°-30°-30°-30°=90°。可见让学生回想做过的题目，能在巩固认知的同时，进一步深化思维。

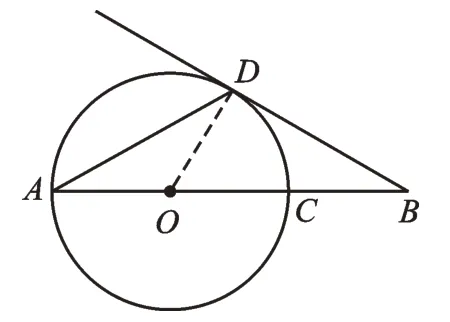
图3

经过笔者的教学实践，学生学会了自我“搭桥造船”去解决问题，一题多想，举一反三，提高了学习效率。当然，笔者在教学反思中也发现了一些需要改进的地方。例如，要结合学生实际能力，循序渐进地训练学生这方面的能力，不能急于求成；不能两极化，学生的练习量要适度保证。

学生才是数学学习过程中最需要关心的主体。因此教师在教学中要时刻关注学生的学习过程，让他们得到最大限度的发展。让学生一题多想，既是在减轻学生的学习负担，又是在提升他们的思维品质和扩散思维能力。在尊重学生身心健康的同时，给予他们最适切的教育，从而让学生喜欢上数学，发挥其主动性，探究数学的奇幻之美。