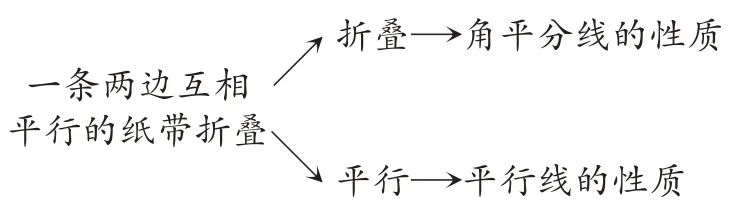
透视折叠的纸带

文周淑芳

（作者单位：江苏省无锡市西漳中学）

在“平面图形的认识（二）”这一章中，有些同学怕做折叠类题，生怕出错。周老师现挑出折叠问题中的一个典型案例与同学们分享，以期帮助大家理清思路，正视错误，引以为戒。

例题如图1，一条两边平行的纸带折叠后仍在同一平面内，已知α=76°，则∠1=（ ）。

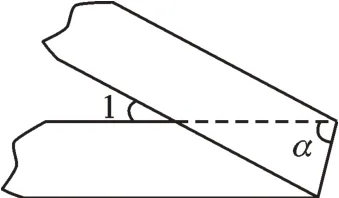
图1

A.28° B.30° C.38° D.45°

【错误】错误1：猜测∠1 与α 互余，没有选项可选，随便选择一个选项。错误2：度量∠1 的度数，凭经验取整得选项B。

【错因】找不到角与角之间的关系；想把折叠前的纸带重新画出来，但画图不准确，难以入手。

【解析】题目的情境是一张折叠的纸带，“互相平行”这个条件不容忽视。本题的关键词有两个：折叠与平行。折叠，前后图形一样；平行，三类角关系确定。

如何把折叠的纸带还原图画出来呢？动手折叠，打开直观感知，然后抓住原来两边互相平行，不难画出图2。

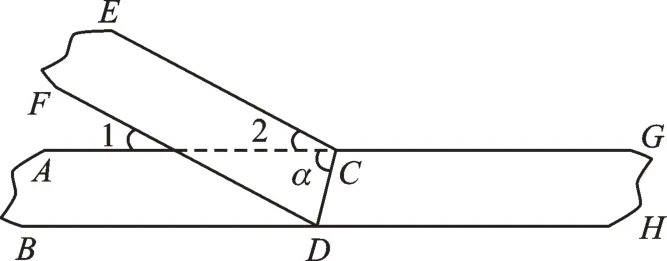
图2

折叠，得到∠GCD=∠ECD=∠2+∠α，由平角的定义得到∠ACD+∠GCD=180°，即∠2+2∠α=180，解得∠2=28°，根据纸带平行得CE∥DF，由其性质得∠1=∠2，最后求得∠1 的度数为28°。当然，也可以由平行得到∠CDH=∠α，折叠得到∠CDH=∠CDF，进而求得∠FDB，由平行得∠1=∠FDB。

【总结】折叠的问题，可以转化为角平分线的问题，折痕所在直线即为角平分线，再综合运用平角的定义与平行线的性质即可解决问题。

【练习】图3 是长方形纸带，∠DEF=15°，将纸带沿EF折叠成图4，则∠AEG=______度，再沿BF折叠成图5，则图中的∠CFE=______度。

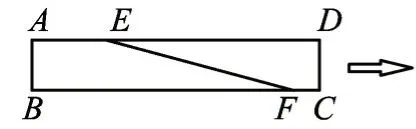
图3

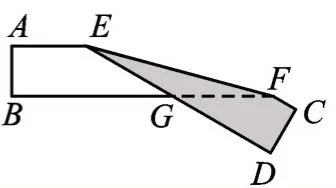
图4

图5

【解析】先将图4还原成折叠前的纸带，折痕EF就是角平分线。

图3

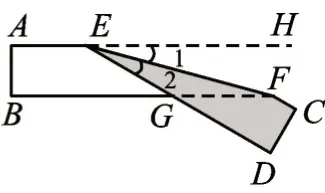
图4（还原）

则∠1=∠2=15°，因此∠AEG=180°-2×15°=150°。

再将图5还原。

图3

图4（还原）

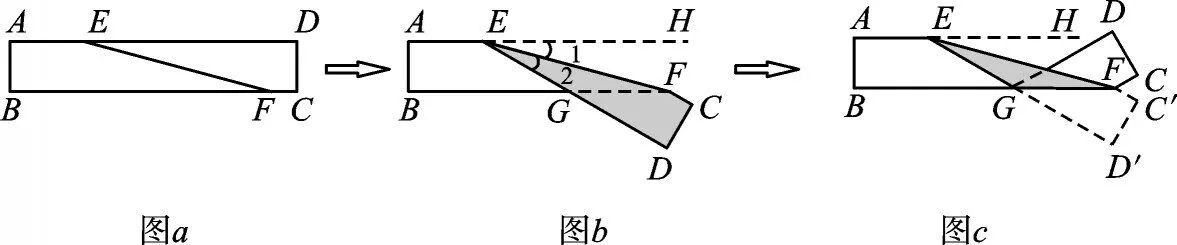
图5（还原）

第二次折叠后不难发现折痕GF也是角平分线，

∴∠FGD′=∠FGD，

∴∠GFC′=∠GFC。

由于纸条是长方形，

∴AH∥BF，FC′∥ED′，

∴∠EFG=∠FEH=15°，

且∠EFC′=180°-∠FEG=165°，

∴∠GFC=∠GFC′=165°-15°=150°，

∴∠CFE=∠GFC-∠GFE=150°-15°=135°。

【总结】折叠纸带问题考查的知识点是平行线的性质，难点是转化为角平分线问题，关键是画出还原图。具体思路是：画出还原图，折痕即角平分线；结合平行性质，找到角之间的数量关系。思路如下：