助推儿童数学表达力进阶的实践探寻

顾万全 陈静

【摘 要】当下，在数学学习中，不少儿童存在着不敢说、不会说、会说但不会写、会说会写但流于浅表层等问题。在数学教学中，教师可以从激发儿童的问题意识，引导儿童建立表达框架、明晰表述方式，促进儿童深层表达等方面着手，助推儿童的数学表达力进阶，促进他们敢说、会说、说好。

【关键词】数学表达力;表达力进阶;表达框架;表述方式

【中图分类号】G623.5  【文献标志码】A  【文章编号】1005-6009（2021）86-0038-04

【作者简介】1.顾万全，江苏省淮安市淮海小学（江苏淮安，223001）党委书记、校长，高级教师，淮安市数学学科带头人，淮安市优秀教师;2.陈静，江苏省淮安市淮海小学（江苏淮安，223001）德育处主任，一级教师，淮安市德育工作先进个人。

《义务教育数学课程标准（2011年版）》阐述数学课程总目标时从四个方面展开，分别是知识技能、数学思考、问题解决和情感态度。这四个类别中都对学生的“表达力”提出了要求：知识与技能方面要求引导学生经历探究讨论的过程;数学思考方面要求学生能清晰地表达自己的想法;问题解决方面要求学生学会与他人合作交流;情感态度方面要求学生养成合作、交流等学习习惯。表达力不仅是指能语言流畅地说出自己知道的知识，更是指能正确地陈述自己的想法和观点，它是学生发现和提出问题、分析和解决问题能力及数学思维能力成长的外化，是其碰撞思维、建构认知、提升数学思考能力的深度学习的促进。然而，笔者在教学实践中发现，儿童普遍存在着不敢说、不会说、会说但不会写、会说会写但流于浅表层等问题。因此，笔者认为，教师在教学中有意识地助推儿童的数学表达力进阶势在必行。

一、儿童数学表达力进阶的内涵与价值

数学表达力，是指学生在数学学习活动中，基于数学知识，用口头语言或书面的文字呈现、字母表示、符号表征等方式陈述数学观点及结论，并在发现、提出、分析和解决问题的过程中呈现出的表现力。儿童用数学语言表达世界是在其用数学的眼光观察世界（外界输入）、用数学的思维分析世界（自身处理）的基础上的对外输出。

在小学阶段，儿童的数学表达力发展大致经历如下页图1所示的四个阶段。儿童数学表达力的层级化进阶，是其数学思维由混沌走向清晰、由经验走向理性、由浅表走向深入、由从众走向内省思考的过程，是其在数学化思考中，数学思维发生质的飞跃，成长为有“数学味”的人的过程。笔者所研究的表达力进阶，主要表现在表达情感进阶、表达方式进阶与表达思维进阶等方面。表达情感进阶指的是由不敢说到敢说、喜欢说;表达方式进阶指的是由口语化地说、简单地说进阶到多元表征（文字、符号、动作、操作）地说;表达思维进阶指的是由浅层的儿童化思考到有数学逻辑推理、模型化思维表达的思考。推动儿童的数学表达力进阶，有助于激发儿童的问题意识，使他们放心说、开心说;有助于儿童建立表达框架、明晰表述方式，使他们数学说、完整说;有助于儿童建立深层表达，使他们深度说、思维说。

二、儿童数学表达力进阶的实践探寻

（一）从氛围到方式，让学生敢说

1.营造民主氛围，促进师生情感交融。

心理学提倡以积极的态度激发人的内在潜力，以积极的情绪体验引导学生在学习中经历“习得性成长”。在包容的安全环境中，在轻松、愉悦的睦恰氛围里，在教师的正向鼓励下，儿童将会从不敢表达、不会表达向敢表达、能表达进阶。如教学“乘法分配律”时，教师呈现有问题的学生资源：125×3+125×5=125×3+5。

师：从左到右的转换，参与计算的哪道式子没变，哪道式子变了？

生1：参与计算的125×3没变，但原式加的是125×5，被变换成了只加5。

师：你对算式的敏锐观察和比较很让人欣赏哎！其他同学有自己的“转化”窍门吗？

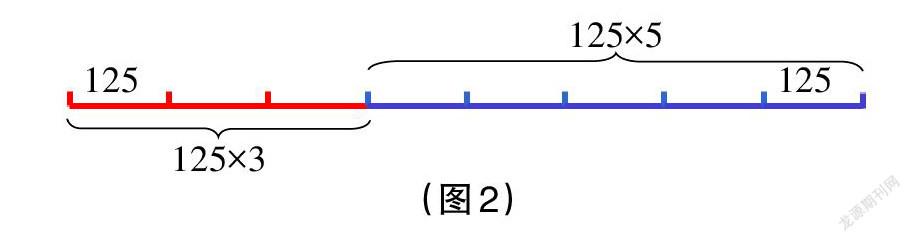
生2：我们二年级时就研究过“乘法是加法的简便运算”，这位同学直接丢掉一个乘数，只留下了一个乘数。我想画个线段图（冲到黑板前画出图2），一目了然。所以呢，125×3+125×5=125×（3+5）。

师：除了线段图，平面图或立体图能呈现出正确的思考吗？

生3：我可以用“求长方形面积”的方法试着画个平面图（走到黑板前画出图3）。通过观察图形，很容易发现，两道乘法算式相加，其实就是两个小面积相加。大面积=小面积+小面积，而不是只加一条宽。

师：你从面积的角度去思考，另辟蹊径，很好呀！如果不画图，你的思考又是什么样的呢？

生4：我会想，我们采购表演服每件125元，男生需要3件，女生需要5件，总价肯定不可以是3件的价格加数量5呀！

师：是的，要加数量5件的价格。

…………

学生对错题剖析的思考表达既有生活经验也有数学认知，教师对学生表达意图的准确解读和认同，使得学生愿意坦率地表达出自己的数学思考。学生将观察到的算式形式及数字特征在脑海中进行图式表征后，在教师“问题链”的引领下调取长时记忆中的相关图式，更易于递等出“125×3+125×5=125×（3+5）”這个算式，进而巩固对“a×c+b×c=（a+b）×c”这一字母形式的理解，从源头上强化对乘法运算律的数学化思考。

2.建构表达框架，促使学生述有结构。

史宁中教授指出：数学教育的终极目标，是引导学生会用数学的眼光观察世界，会用数学的思维思考世界，会用数学的语言表达世界。在数学课堂中，师说我说（用嘴巴表达）—现象陈述（用眼睛表达）—发现规律（用头脑表达）—反思归纳（用思维表达），学生的层级式表达是其伴随着数学思考进入深度学习的标识，数学表达力进阶有助于学生数学核心素养的发展。为了让学生动口说、动手写的过程更具逻辑性和思维性，笔者与学生商定，将“我有表达”“我有思考”“我有疑问”“我有不同意见”等话术作为数学课堂的引语，且书写于黑板固定处，便于他们参照。

四年级学生接触“25×（40+8）”这道题时，笔者鼓励他们“根据这道算式思考并列举一个生活中的例子”，学生举例道：一盒饼干25元，小明想跟同学们分享，第一次买了40盒，第二次买了8盒。请问一共需要付多少元钱？接着，笔者提议出题小老师邀请一位同学来解答。学生借助“我有表达”“我有补充”“我有不同意见”等话术互相启发思考，当先算（40+8）与先分别算25×40、25×8这两种方法都出现时，笔者追问：想一想，这两种计算方法为什么都可以算出一共付了多少钱？请你联系生活经验，说一说。

生1：我先算出两次一共买了多少盒，再用单价×数量=总价，算出一共付了多少钱。

生2：我有表达，用单价×数量=总价，分别算出第一次和第二次买要花多少钱，再相加算出总价。

生3：我有补充，在生活中，两种计算方法都可以。但是，到底哪种方法更便捷呢？我们要有自己的思考。

师：谁来猜猜“我们的思考”是什么？

生4：我觉得“我们的思考”是，当总盒数相加的和是整十、整百或整千时，先算总盒数比较便捷;当单价和每次购买的盒数相乘能得整数时，分开计算价格的方法比较便捷。

上述交流环节，学生单个体多频次、单个体与同伴之间、单个体与教师之间经历了“现象陈述—对比分析—反思归纳”的过程，将生活经验与深度学习有效地链接了起来，激发了学生自发调取生活经验参与思考运算律内在机理的意识，使学生的表达更会架构、更有逻辑。

（二）从单一到多元，让学生会说

1.口头表达与书面表达相结合。

师生对话、生生对话、生本对话均指向学生的口头语言表达。在实际教学中，我们会发现，学生会说但不会书面输出的现象比比皆是，其实，写、画也是提升儿童表达力的重要途径。四年级学生“初见”加法、乘法运算律后，因生活情境的唤醒、数形结合等方法的使用，有教师就以为学生已经通透地了解了算理。同时，因为数学课堂的时间有限，教师多以“齐说”“优生说”替代“个体说”。

笔者以前教学“运算律”时，注重学生体验基础上的个体反馈式口语表达。学生在课堂上一直是活跃和互动的，但在落笔书面表达时，亦会出现不少错误，如：①257×31-57×31=（257+57）×31;②25×（40+8）=25×40×8;③25×32=25×（4×8）=25×4+25×8;④125×3+125×5=125×3+5;⑤303×21=（300+3）×21=303×21。究其原因：①缺乏严谨的作答态度;②③算理不清;④逆向思维受阻，等量意识欠缺;⑤规律感知不明。

这次教学时，笔者在保持课堂上学生口头表达频次的前提下，引导学生将口头表达与书面表达相结合，并呈现上述错误题目，要求学生“挑选其中的一道题，将它的错处说给同桌听。然后重新列递等式解答，并用自己喜欢的方法（写一写、画一画）表示出来”，以保证课堂上所有学生既能说又真正参与写、画、算的书面表达活动，算理的理解、算法的掌握、算技的思考在口语表达与书面表达相融合的过程中得到了有效落实。

2.文字表达与符号表达相融合。

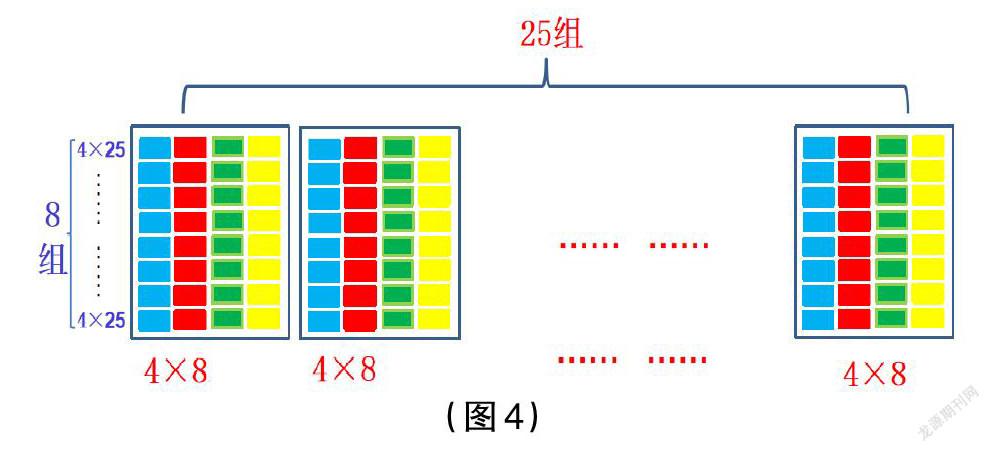
学生的数学学习过程，其实也是其多元表征能力成长的过程。由情境到圖形，由图形到算式，由算式到符号，由符号到自己列举可简算的题目，是学生数学建模思维的外显。学生“25×（4×8）=25×4+25×8”这道题中呈现出的偏差思考，起码说明他们有“见到乘数25想到乘数4”的简算意识，在乘法中杂糅加法则暴露出学生在算理方面的不清晰。乘法结合律和乘法分配律的混用，与学生缺乏对“为什么能简算？用什么去简算？”这类问题的思考有关。教师在追问学生“怎样去简算”之前，以如图4所示的引导性文字与多角度符号启发学生展开思考，可以更好地促进他们自主挖掘知识内涵，建构知识模型。

（三）从表层到深层，让学生说好

学生动口说和动手写的情感、方式的进阶，均指向学生的数学思维由混沌走向清晰、由经验走向理性、由从众走向内观，并最终由表层走向深层的“智说”的过程。笔者主张教师在教学中与学生一起经历角色体验、全程互动，强调民主平等、潜能激发，并注重给学生提供提一些问题、做一项任务、作一次交流、当一回老师的机会。学生对某一知识点的学习，不能仅就知识学知识，还要知道该知识点的前沿后续。如运算律的知识不是仅出现在四年级，不能割裂地对其进行教学。从思维训练来看，它建构于学生对三年级“减法的性质”“除法的性质”的体悟，广泛应用于六年级整数、分数、小数的学习中;从思维建构来看，它还可以融通初中负数介入后的算理。数学学科本质要求我们，要超越简单的具体知识，理解其背后的结构、方法和思想。四年级学习运算律时适当渗透其相关知识，有助于学生对知识的思考走向深入。教师要注意引导学生在交流分享中实现深度学习、智慧表达。

数学家陈省身先生说：“数学是自己思考的产物。首先要能够思考起来，用自己的见解和别人的见解交换，会有很好的效果。”学生通过表达学习数学，通过数学学习学会思考，通过思考表达世界。情感交融、建构框架、口手融合、文符融合、文图结合等有助于学生敢说、会说、智说，实现数学表达力的进阶式提升，从而使其数学思考逐渐走向深入。

【参考文献】

[1]姚晶晶.提升儿童数学学习“表达力”的实践与探索[J].小学数学教师，2020（1）：21-25.

[2]郑毓信.数学深度教学的理论与实践[M].南京：江苏教育出版社，2020.

[3]余文森.核心素养导向的课堂教学[M].上海：上海教育出版社，2017.

3786500589279