基于改进果蝇优化算法的ECT 图像重建方法∗
田 鹏崔丽琴王耀萱秦 龙秦建敏
(太原理工大学物理与光电工程学院,山西 太原 030024)
电容层析成像技术(Electrical Capacitance Tomography,ECT)作为一种新兴的无损检测方法,具有结构简单、无辐射、响应速度快、成本低等优点,已被广泛应用于油气管道、循环流化床、制药工艺等多相流检测领域,具有很高的实际应用价值[1-4]。
ECT 系统一般由电极阵列传感器、数据采集单元以及图像重建单元三部分组成[7]。 其中图像重建单元是ECT 系统中非常关键的环节,重建结果的质量很大程度上取决于图像重建算法的性能。 目前常见的算法可分为直接算法、迭代算法和智能算法。直接算法包括线性反投影算法(LBP)[9]、Tikhonov正则化算法(TR)[11]、截断奇异值算法(TSVD)[12]等;迭代算法包括Landweber 算法(LI)[14]、共轭梯度算法(CG)[15]等。 其中LBP 算法简单,运行速度快但成像精度差,结果存在大量伪影,常被用作其他算法的初始解;TR 算法基于正则化技术,将原始问题转化为一个带稳定泛函的优化问题,可以有效减弱ECT 图像重建的“病态性”,但是同时会存在解过于光滑、不能很好地保留图像边缘信息的问题。 LI算法基于最速梯度下降原理,速度较快,但是往往需要多次迭代才可以获得较好的重建结果,并且受到半收敛特性的限制。 针对传统算法存在的不足,近年来国内外学者将遗传算法、蚁群算法、粒子群算法等智能算法应用到ECT 图像重建领域,提出了许多改进算法。 张立峰等将遗传算法与极限学习机结合起来确定最佳权值和阈值,增强了算法的准确性和实时性,进一步提高了对两相流不同流型的辨识精度[17]。 陈宇等提出一种遗传蚁群算法对ECT 边界进行灰度补偿,增强了成像稳定性,提高了重建图像质量[18]。 赵玉磊等考虑到ECT 的“软场”特性,通过支持向量机得到关于不同流型的先验信息,提出一种基于双粒子群竞争的图像重建算法,能够提高重建算法收敛性和鲁棒性以及重建图像的精度[19]。Deabes W 等利用粒子群优化算法获得模糊隶属度函数的最优参数,克服了ECT 系统的非线性特性,并能提高重建速度。 与传统图像重建算法相比,该算法能更好地保留图像的边缘和细节,在视觉效果和成像质量方面都有较好的表现[20]。 上述几种方法是基于不同优化算法进行的改进ECT 重建方法研究,每种方法具有各自的优点,能够对图像重建实现不同的提升效果,但是也存在某些局限性,比如参数设置较多,对训练样本要求较高等。
本文考虑到果蝇优化算法(FOA)具有原理简单易懂、参数设置少、局部搜索能力较强的独特优势,同时为了获得伪影更少,精度更高的重建图像,提出一种基于改进型果蝇优化算法(Improved Fruit Fly Optimization Algorithm,IFOA)的ECT 图像重建方法。 首先对果蝇的位置函数进行了更新,避免了味道浓度不能为负值的缺点;其次将个体果蝇的历史轨迹引入到寻优过程中,随着迭代次数不断增加,个体向自身寻优轨迹的学习程度也逐步增强;接着采用自适应搜索步长来代替标准FOA 中的固定步长,来平衡算法的全局搜索能力和局部搜索能力;最后引入了带正则化项的适应度函数,更好地处理ECT 图像重建这一病态问题。 为了提高算法的收敛性,将TR 算法的重建结果作为IFOA 的初始解,提高重建图像质量。
为了验证本文提出算法的有效性,设置六种不同流型作为重建目标,并与LBP 算法、TR 算法以及LI 算法的重建结果进行比较。 仿真实验结果表明,本文方法不仅可以有效减少重建图像中的伪影,而且图像的相对误差以及相关系数均得到提升。
1 ECT 原理与仿真模型
电容层析成像的目的是通过灵敏度矩阵和测量电容值恢复出场域内的介电常数分布,其求解过程包括正问题求解和反问题求解。 正问题求解是利用已知的传感器参数,介电常数分布以及边界条件来获得不同极板对之间的电容值,即:

Landweber 算法基于最速梯度下降原理,可以有效提高图像重建精度,但是受到半收敛特性影响,其具体过程如下:

2 改进果蝇优化算法
果蝇是一种嗅觉非常发达的生物,能够闻到40 km 外的食物气味,当它接近食物位置附近后亦可使用敏锐的视觉发现食物和同伴聚集的位置,并且向该方向飞去。 果蝇优化算法正是基于果蝇觅食行为而提出的新兴群体智能优化算法,寻优过程可分为嗅觉搜索阶段和视觉搜索阶段,图1 为果蝇搜索食物的过程,相对于粒子群优化算法、遗传算法、蚁群算法等其他群智能算法,FOA 的原理简单易懂,需要调节的参数更少,具有较强的局部寻优能力,因此被广泛应用于许多工程优化问题[21-24]。
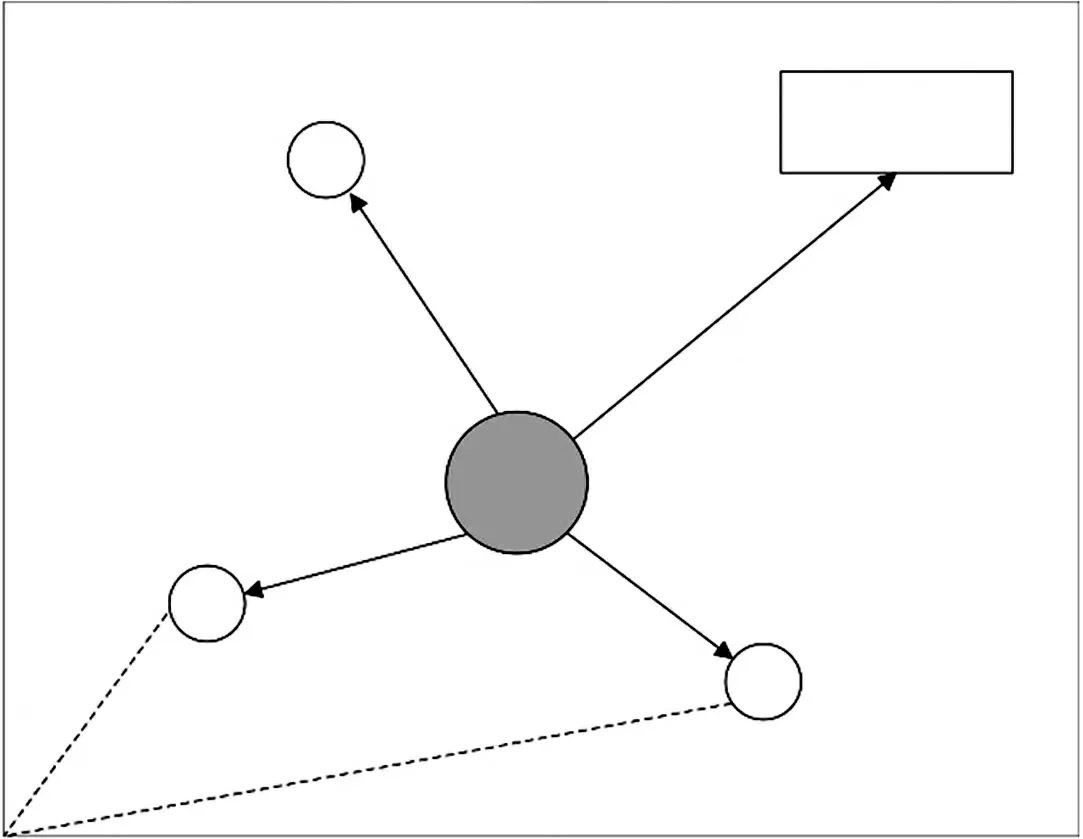
图1 FOA 示意图
标准FOA 迭代具体步骤如下:
Step 1 首先设置果蝇种群规模sizepop,最大迭代次数maxgen,并赋予果蝇随机初始位置Xaxis,Yaxis。
Step 2 果蝇利用嗅觉进行搜索,赋予每个果蝇随机的搜索方向和距离。

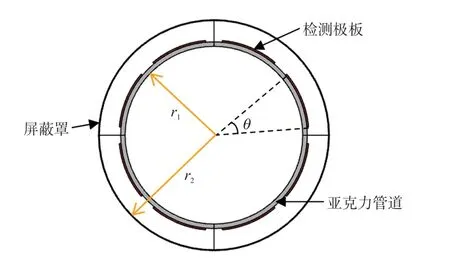
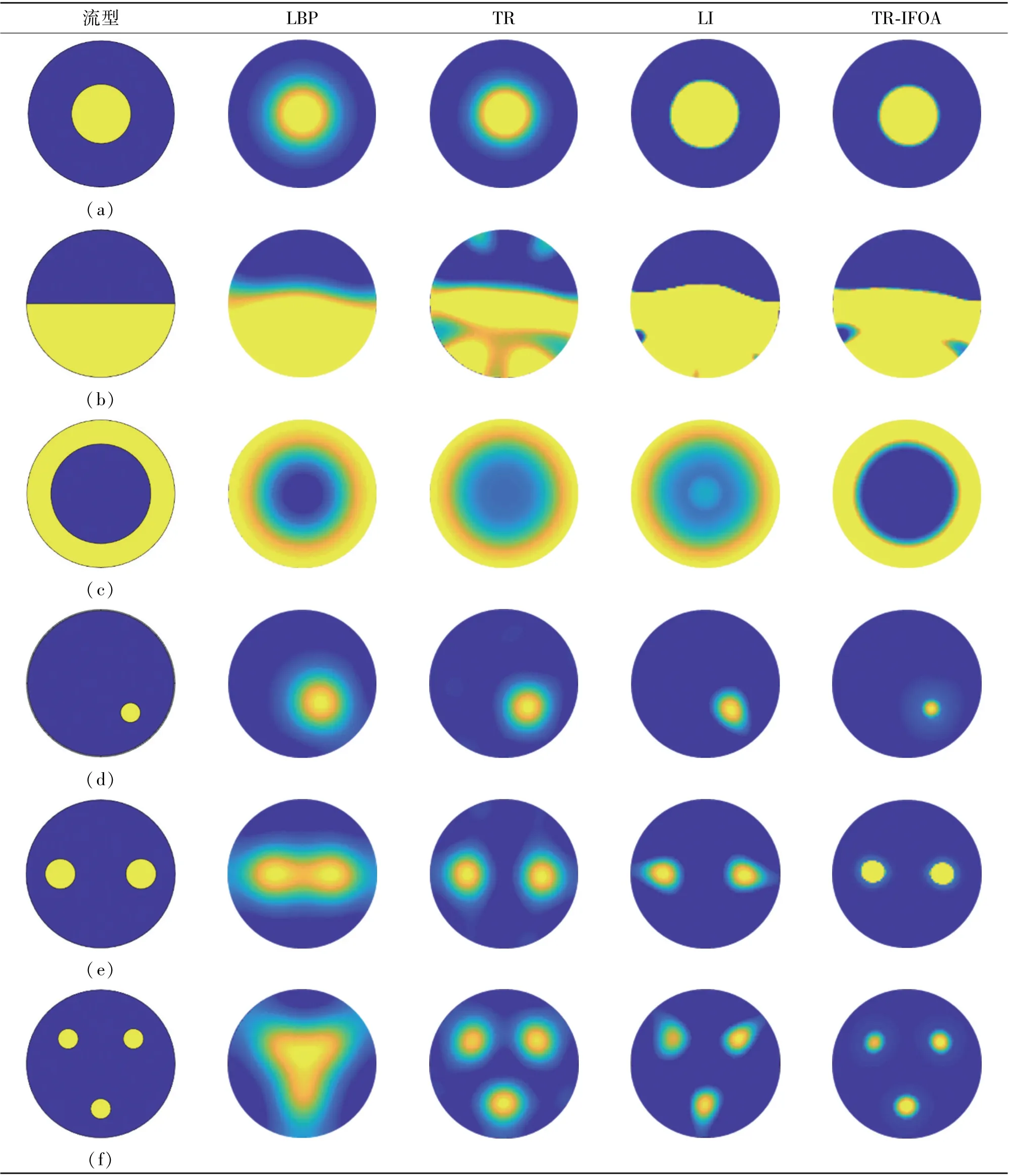
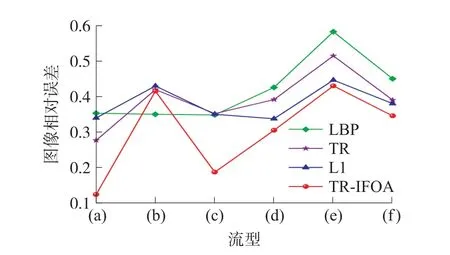
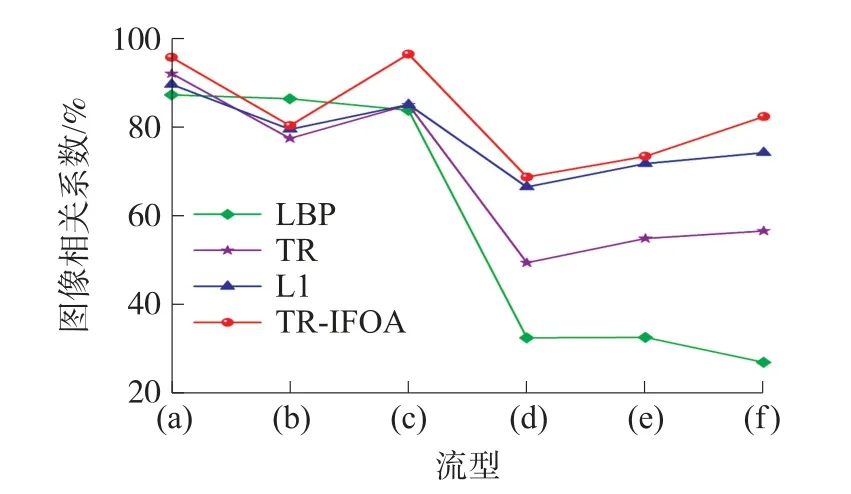
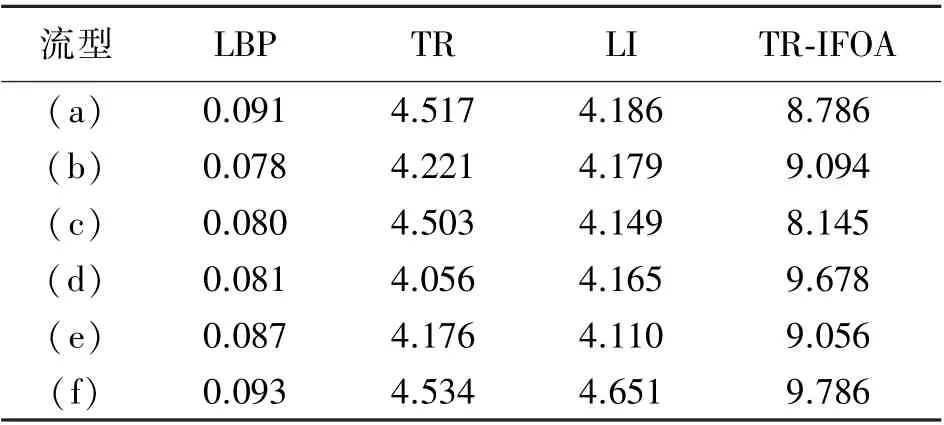
Step 6 判断果蝇气味浓度值是否比上一代更优,即Smellbest Step 7 重复Step 2~Step 6,直到满足最大迭代次数。 标准FOA 虽然具有较强的局部寻优能力,但其全局搜索能力较弱,在迭代过程中容易陷入局部最优,尤其在处理复杂高维优化问题时,更易产生收敛过早的问题。 针对以上不足,本文对标准FOA 进行了相应改进,并与TR 算法相结合,提出一种可用于ECT 图像重建的改进果蝇优化算法,即TR-IFOA。 本文提出的新算法将从以下四个方面对标准FOA 进行改进: ①对于标准FOA,由于气味浓度判定值Si的定义是果蝇位置到原点距离的倒数,因此嗅觉浓度不能为负值,导致算法只能在解空间的正部分进行搜索,无法解决最优值为负数的优化问题,且只能围绕原点附近运动。 为了克服上述不足,本文中果蝇的空间位置采用Xi(xi1,xi2,…,xid)来代替标准FOA 中的Di,d为解空间的维度,本文中为像素点总个数,因此果蝇的气味浓度判定值Si=Xi。 ②标准FOA 在迭代过程中只向种群中的最优个体学习,即每一次迭代,所有果蝇都向同一位置聚集,忽略了个体果蝇自身的历史寻优轨迹,导致算法容易陷入局部最优,精度不高。 因此本文将个体果蝇的历史最优位置Xpbest引入到迭代搜索过程中,随着迭代次数增加,利用动态权重因子w1不断增强向自身历史轨迹的学习,从而提高算法的收敛精度。 ③标准FOA 在整个迭代过程中,总是以固定步长进行随机搜索,在迭代后期很容易错过全局最优解。 在果蝇觅食的初始阶段,果蝇群体的位置往往远离全局最优解,因此需要保持较大的搜索步长,来增强算法全局探索能力;随着迭代次数增加,种群的中心位置接近最优解,因此需要较小的步长来提高局部搜索能力。 因此本文中使用了自适应步长代替标准FOA 固定步长的搜索策略,利用步长调整系数w2动态调整果蝇的搜索范围,使得算法在迭代初期具有较大的搜索半径,后期具有较小的搜索半径,可以更好地平衡果蝇的全局搜索能力和局部搜索能力,提高算法的收敛性。 ④由于ECT 反问题的病态性,本文采用TR 算法作为图像重建初始解,并在适应度函数中引入正则化项。 利用IFOA 对初始解进行优化,可以减轻TR 算法所导致的解过于光滑以及图像边缘模糊的问题,进一步提高重建图像精度。 本文提出的TR-IFOA 具体步骤如下: Step 1 设置果蝇种群大小sizepop,最大迭代次数maxgen 以及初始搜索步长L。 Step 2 利用TR 算法得到的重建结果作为果蝇种群的初始位置。 Step 3 利用式(8)更新果蝇的位置,其中Xipbest为第i个果蝇的历史最优位置,L=1 为固定搜索步长;wmin和wmax为系数w1的最小值和最大值,本文将其分别设置为0 和1.5,g为当前迭代次数;t=1 为搜索步长衰减因子,用来控制步长衰减速率;rand( )为[0,1]内随机数。 Step 6 开始果蝇迭代搜索,重复Step 3~Step 5,直到满足最大迭代次数。 本文利用COMSOL Multiphysics 5.4a 有限元分析软件建立八电极ECT 传感器仿真模型,如图2 所示。 设置传感器的参数:管道内半径r1为100 mm,管道厚度为5 mm,屏蔽罩半径r2为130 mm,电极张角θ为35°。 成像区域内重建图像的像素点个数设置为81×81。 所有算法均在MATLAB2019a 中执行。 图2 ECT 传感器结构图 为了验证提出算法的有效性,本文将设置六种不同的流型作为重建目标,如表1 中的(a)~(f)所示,并选择LBP 算法、TR 算法、LI 算法的重建结果作为对照组。 通过比较不同算法的成像效果,总结出本文算法的优势与不足,其中TR 算法中的正则化参数设为0.05;LI 算法的迭代步长以及迭代次数分别设置为100 和1。 此外,为了客观评价重建质量,采用图像相对误差(RE)以及相关系数(CC)作为重建图像定量评价标准,二者定义分别如下: 从表1 可以看出,LBP 算法重建的图像存在较多伪影,且无法确定物体的准确大小和位置,对于流型(e)和(f),无法区分多个成像目标。 TR 算法相对于LBP 算法,重建图像中的伪影有所减少且可以区分开不同成像目标,但是依旧无法反映出物体的真实大小,且对于流型(b)的成像产生了内部形变。LI 算法重建图像的伪影相对较少,对于流型(a)的成像效果较好,但是对于流型(d),(e)以及(f),重建结果出现了明显拉伸变形。 使用本文提出的TRIFOA 重建流型(a)和流型(d),相对于LBP 算法和TR 算法,可以减少重建图像的伪影,相比于LI 算法,重建图像形状更接近原始流型分布;对于流型(b),与LBP 算法相比,重建图像伪影减少,与TR算法相比,重建图像的伪影和内部形变均有所减小,而相对于LI 算法,边缘凸起更加平缓,但内部形变较大;流型(c)的轮廓比其他对比算法的结果更加清晰;对于流型(e)和(f)多个成像目标的重建,图像中的伪影得到有效减少,重建目标的大小以及形状更接近真实情况。 表1 不同算法的重建图像 图3 为重建图像相对误差的对比图,通过分析可以看出,相对其他几种算法,本文提出的算法可以降低图像相对误差,但是对于不同流型的误差降低程度不同,比如对于流型(c)的降低比较明显,对于流型(b),相对TR 和LI 算法,相对误差有所降低。图4 为重建图像相关系数的对比图,同样地,对不同流型的相关系数提升程度不同,流型(c)的提升比较明显,而流型(b)的相关系数变化较小。 出现这种情况的原因,可能是由于果蝇在搜索过程中,集中在了流型的某些特定位置,对相对误差和相关系数产生不利影响。 图3 不同算法重建图像相对误差对比 图4 不同算法重建图像相关系数对比 以上数据分析表明,本文提出的TR-IFOA 可以提高图像重建精度,减少伪影,更好地保留图像边缘细节,对于图像相对误差以及相关系数都有一定程度的改善效果。 表2 为不同算法的重建速度,由于是先利用TR 算法计算初始解,再执行改进FOA 迭代过程,因此本文方法在成像速度上不占优势,这也是未来需要继续优化的方向。 表2 不同算法图像重建速度s 考虑到TR 算法在ECT 图像重建过程中,存在解过于光滑及图像边缘模糊的问题,本文提出一种改进果蝇优化算法,通过与TR 算法相结合对ECT图像重建问题进行求解。 针对标准FOA 局部搜索能力较弱,收敛精度不足的问题,作者采用新的果蝇位置函数,用自适应的搜索步长替代固定步长,并将个体果蝇的历史优化轨迹考虑在内,最后在适应度函数中引入正则化项,对标准FOA 进行优化改进。为了验证新算法性能,对六种不同的流型进行了仿真实验,并与经典算法中的LBP 算法、TR 算法和LI算法的重建结果进行了对比。 结果表明,TR-IFOA可以有效减少重建图像中的伪影,更好地保留边缘信息和图像细节,进一步提高图像重建质量。 同时,本文算法也存在一些不足之处,比如对不同流型的改进程度不同,对于流型(b)的提升效果并不明显,未来还需要对新算法的适应性做进一步提升;除此之外,该算法依旧存在一定的随机性,这也是下一步要解决的问题之一。

3 结果与分析

4 结论

