基于全卷积网络的阀门粘滞检测方法

解剑波，范海东，李清毅，刘梦杰，赵春晖

（1.浙江省能源集团有限公司，杭州 310007；2.浙江大学 控制科学与工程学院，杭州 310027）

0 引言

现代社会的正常运转离不开电能，在我国的电力产业中，每年火电发电量约占总发电量的70%，火力发电仍然是电力产业的支柱，是我国经济发展的重要支撑。随着计算机技术与自动控制技术的发展，火电厂中的自动化程度也在逐渐提高，每个工厂中都有数以百计的自动控制回路。每条自动控制回路在投入正式运行前都经过精心设计，以保证回路的控制性能良好。然而在日常运行过程中，回路中的设备难以避免地会出现老化等问题，这些问题可能会导致回路的控制性能下降，降低回路的生产效率，进而影响到整个工厂的经济效益。

阀门是回路中最常见的执行元件，自动控制回路中的控制器通过调节阀门开度的大小，对回路的过程变量进行控制。正常的阀门在运行时是线性的，阀门的实际开度能够很好地跟随控制信号变化，但是由于内部元件磨损等问题，阀门在运行一段时间后可能会出现非线性特性，如磁滞、死区、粘滞等，其中，粘滞是最常出现的问题[1]。阀门粘滞往往会导致回路出现振荡，降低回路的控制性能，而依靠人工对工厂中的每个阀门进行粘滞检测会浪费大量的人力物力。因此，如何利用控制回路中的数据进行自动化阀门粘滞检测成为控制回路性能监控与诊断领域的一个重要问题。

在过去几十年中，许多学者研究了阀门粘滞的检测方法，主要可以分为以下4 类[2]：基于互相关函数的方法[3]、基于极限环模式识别的方法[4]、基于非线性检测的方法[5]以及基于波形的方法[6]。Horch[3]提出了基于CCF（互相关函数）的方法，如果OP（控制器输出）与PV（过程变量）间的互相关函数为奇函数，那么回路中的振荡是由阀门粘滞引起的，否则，振荡是由其他原因引起的。郑丽丽等人[4]提出了一种改进的基于模糊聚类的粘滞检测方法，首先对OP-MV（操纵变量）图使用模糊聚类算法获得4 个聚类中心，然后对聚类中心所构成四边形进行凹凸性识别，最后根据聚类中心的分布特征定义了一种新粘滞指标。Choudhury 等人[5]先使用基于双相干谱函数的方法[6]诊断回路中的振荡是否由非线性原因所引起，当是由非线性原因引起时，使用椭圆对滤波后数据对应的OP-PV 图进行拟合，若成功地拟合出椭圆，则说明回路振荡的根本原因为阀门粘滞。He 等人[7]使用曲线拟合的方法进行粘滞检测，分别使用三角波和正弦波对OP 经过第一个积分作用后的信号进行拟合，并根据两种拟合的误差对比得到粘滞检测结果。上述经典的粘滞检测算法虽然能够取得不错的粘滞检测结果，但通常适用范围有限，如Horch 的方法只适用于使用PI 控制器的非积分过程。

在最近几年中，神经网络被广泛应用于故障检测与诊断领域[8-10，13-15]，也有学者提出使用神经网络来解决阀门粘滞检测问题。Dambros 等人[11]将回路的OP-PV 图转化为8×8 像素的图片，并训练一个人工神经网络对该图片进行分类，最终可以得到回路的诊断结果为无振荡、粘滞引起的振荡或其他原因引起的振荡。而Henry 等人[12]提出了一种基于CNN-PCA 的粘滞检测方法，首先使用CNN（卷积网络）提取数据对应的无阈值递归图中的特征，然后使用PCA（主成分分析）模型对应的特征统计量进行阀门粘滞的检测。以上方法在神经网络输入数据构造的过程中都难以避免地会损失部分过程数据本身包含的信息。

为了解决上述方法的不足，提出了一种基于FCN（全卷积网络）的阀门粘滞检测方法。首先，回路中的原始运行数据包含着丰富的过程动态信息。其次，相较于传统的人工神经网络，使用卷积神经网络能够更好地处理多变量时间序列数据中的时序关系以及变量间的关系。因此，本文所提的方法直接使用回路运行时的OP 与PV 数据来进行阀门粘滞检测，并使用全卷积网络来解决这个分类问题。

1 阀门粘滞仿真数据生成

1.1 阀门粘滞模型

阀门粘滞现象指的是阀杆受到的静摩擦力增加，导致阀杆在运动时暂时卡住，随着控制信号变化幅度增大，推动阀杆的作用力持续变大，当作用力大于静摩擦力时，阀杆会突然跳跃。阀门粘滞的典型输入、输出特性曲线如图1 所示。

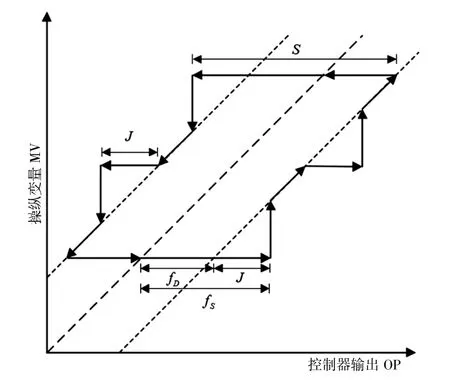
图1 典型的粘滞阀输入、输出特性[18]

常用的阀门粘滞模型主要可以分为两类：基于物理特性的和基于数据驱动的。Brasio 等人[16]总结了基于物理特性的阀门粘滞模型，但是这类方法需要了解阀门的真实物理特性来设置合适的模型参数，并且进行仿真时所需的计算量大，不方便进行仿真。而基于数据驱动的模型则克服了上述缺点，常用于进行阀门粘滞的仿真。文献[2]中对多种基于数据驱动的粘滞模型进行比较，其中，Chen 等人[17]提出的双参数阀门粘滞模型能够更好地吻合阀门在粘滞时的运动特性，本文在后续仿真时也采用这个模型。

1.2 仿真数据生成

训练一个深度神经网络需要大量的有标签数据，然而在实际工业过程中，获得高质量的有标签数据成本极高，所以本文采用仿真模型来生成训练网络时需要使用的数据。

控制回路性能下降的主要原因可以分为控制器参数不佳、外部扰动和阀门粘滞这三类[18]。因此，在进行仿真数据生成时，主要考虑生成控制性能良好以及处在上述三种性能退化情况下的仿真数据。在阀门粘滞的相关研究领域中，有着多种仿真数据生成方法[7，19-20]，其中Choudhury 等人[6]中对上述4 种情况进行过仿真数据生成，此外，Amiruddin 等人[21]使用类似的控制回路模型生成了大量的仿真数据用于后续训练人工神经网络，并取得了良好的效果，本文使用类似的控制回路模型构建方法来进行仿真实验。不过需要注意的是，上述文献中仿真时使用的是Choudhury的阀门粘滞模型[22]，而本文采用的是Chen 的阀门粘滞模型，并对仿真时使用的模型参数进行了修改。

所用仿真模型为一条单输入单输出闭环控制回路，回路模型由PI 控制器、阀门模型、被控对象、噪声以及外部扰动组成，回路中被控对象的传递函数为

当PI 控制器中K=I=0.15 时，该仿真回路的控制性能良好[6]，通过改变K 和I 的值来仿真回路控制性能不佳的情形。此时，模型中控制器的参数设置如表1 所示。

表1 控制参数变化时参数设置

振荡是过程工业中最常见的厂级范围扰动[23]，而由于回路间的低通滤波作用，振荡在经过多个回路传递后会趋向于正弦信号，因此，在回路中添加幅值和周期不同的正弦信号来代表回路受到外部扰动影响的情况，此时回路中的控制器参数为K=I=0.15，回路所受正弦扰动的具体参数设置如表2 所示。

表2 外部扰动情况下参数设置

对于回路中阀门出现粘滞问题的情况，回路控制器参数保持为良好状态，通过改变阀门粘滞模型中粘滞参数的大小来仿真回路受到不同程度粘滞影响时的数据，仿真时具体的粘滞参数设置如表3 所示。

表3 阀门粘滞情况下参数设置

回路在实际运行的过程中，难以避免地会受到噪声的干扰，因此在上述参数已经确定的情况下，回路会在不同的噪声水平下多次进行仿真以生成尽可能真实的数据，噪声方差的取值范围如表4 所示。

表4 噪声方差参数设置

图2 展示了在阀门粘滞参数S=1.75，J=1，白噪声方差V=0.03 情况下仿真生成的OP 及PV数据，图3 展示了对应情况下的OP-PV 图。

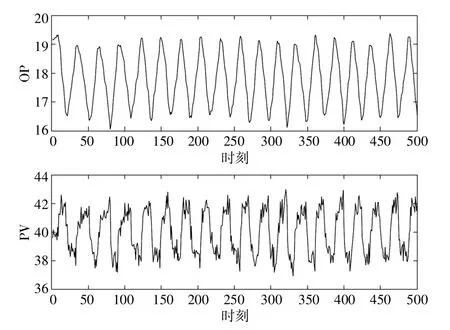
图2 仿真生成的阀门粘滞情况下OP 及PV 数据

2 基于全卷积网络的阀门粘滞检测

2.1 网络输入

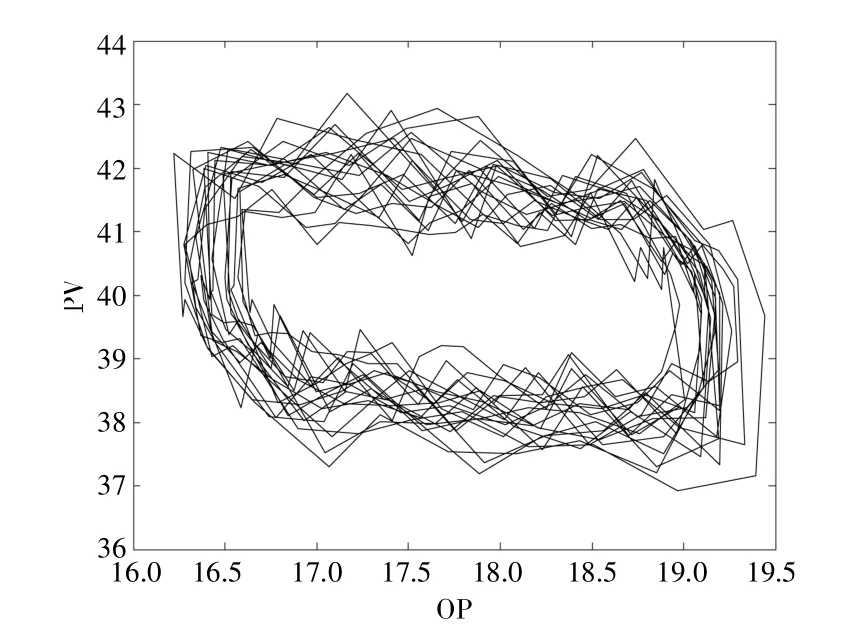
图3 仿真生成的阀门粘滞情况下OP-PV 图

对于使用非智能阀门的控制回路，回路运行时的MV 数据无法直接获得，为了增大阀门粘滞检测算法的应用范围，使用OP 和PV 数据来检测回路中的阀门粘滞现象。而且全卷积网络作为一种可以进行端到端训练的模型，不需要类似传统方法人工提取特征，可以直接使用OP 和PV变量作为网络的输入并获得分类结果。但是由于不同回路中OP 与PV 变量的取值范围有很大差异，有的回路中PV 可以达到上千，而有的回路中PV 可能还不到十，因此本文采用最大最小归一化对2 个变量进行预处理后作为全卷积网络的输入。

此外，在对时序数据进行分类时，每个样本中包含的时间序列长度也会对最终的分类结果产生影响。假如样本中的时间序列长度过短，可能在一个样本对应的时间段内，回路中的阀门一直处于卡涩或者线性运动阶段，哪怕阀门是存在粘滞问题的，但是该样本中的数据并没有包含完整的粘滞阀门运动周期，导致错误的阀门粘滞检测结果。而时间序列长度过长，则会增大运算成本以及提高应用时对于测试样本的要求。因此本文设置每个样本中包含的时间序列长度为500，即全卷积网络的每个输入样本都为回路中OP 变量与PV 变量合并构成的2×500 的矩阵。

2.2 全卷积网络

阀门粘滞检测的目的是通过分析回路运行时的数据，检测出回路中的阀门是否出现粘滞现象。本文将阀门粘滞检测问题看作是一个多变量时间序列分类任务，通过对回路中的多变量数据进行分析，将回路中阀门状态分类为粘滞或者非粘滞。而使用深度学习的方法进行多变量时间序列的分类已经得到了广泛的研究，Fawaz 等人[24]将多种基于深度卷积网络的时间序列分类算法的效果进行了对比，其中，Wang 等人[25]提出的全卷积网络在多变量时间序列分类任务中取得了最好的分类结果。由于全卷积网络的优秀性能，提出了适用于解决阀门粘滞检测问题的全卷积网络。

2.2.1 卷积层设置

多变量时间序列数据中的每个变量都是一个通道，可以直接采用一维卷积对多通道的数据进行卷积操作。由于控制回路中广泛存在时延，即OP 的变化会经过一段时间才影响到PV，因此，具有大的感受野的卷积网络能够更好地捕捉OP与PV 变量间的相对关系，而增大卷积核的尺寸能够直接增大卷积网络的感受野。基于上述介绍，本文使用的全卷积网络中共包含5 个一维卷积层，每个卷积层后都使用ReLU（线性整流函数）作为激活函数，卷积核的尺寸依次为7，5，3，3，3，卷积的步长都为1，且卷积网络中不包含池化层与批标准化层。

2.2.2 分类网络结构设置

在全卷积网络中，卷积层的主要作用为提取数据中的特征，由于在上述网络中经过卷积层后的特征图尺寸与卷积前相同，因此在最后一个卷积层后连接一个GAP（全局平均池化层）来减小特征图的尺寸。相较于使用全连接层，使用全局平均池化层还能够降低网络中的参数量，起到正则化的作用，避免过拟合[26]。

对于全局平均池化层得到的特征，再依次连接一个包含2 个神经元的全连接层以及softmax层以进行分类任务。对于一个输入的样本。全卷积网络的输出可以表示为[y0，y1]，且二者之和为一。

综上所述，全卷积网络结构如图4 所示。

2.3 模型训练

将阀门粘滞检测任务视作一个分类任务，因此可以使用样本真实标签与网络预测结果间的交叉熵作为网络的损失函数。在网络模型构建完成后，将1.2 节中生成的仿真数据作为网络的训练数据，设置仿真生成的非粘滞数据的标签为[1，0]，粘滞数据的标签为[0，1]，使用学习率为0.000 5的Adam 优化算法[27]对网络进行训练，并且在训练时引入权重衰减项以进行正则化。

处于在线阀门粘滞检测阶段时，只需要将待测试回路的数据按照2.1 节所述预处理后，输入到训练完成的网络中，就可以得到该回路的阀门粘滞检测结果，若输出y0大于y1，说明该回路中并没有粘滞问题，否则，说明回路中的阀门出现了粘滞问题。

图4 全卷积网络结构

3 实验分析

3.1 数据案例1

本案例数据来源于浙江省某发电厂的1B 汽泵1 号密封水CP 侧控制回路。汽泵密封水的作用为防止高压高温水从泵内泄漏以及防止低压侧漏入空气。该控制回路采用PID 控制器，过程变量为密封水出口温度，采集了该回路在阀门粘滞情况下运行50 h 的OP 与PV 数据，数据采样的时间间隔为1 s，共计可得到180 000 个时刻的数据。由于构建的阀门粘滞检测网络每次输入的样本包含500 个时刻的数据，因此采用无重叠分段的方法对采集到的数据进行划分，最终可以得到360 个样本。其中第一个样本的OP 及PV 数据如图5 所示，对应的OP-PV 图如图6 所示。

将分段得到的每个样本分别进行预处理后输入之前使用仿真数据训练完成得到的网络中，可以得到这些样本的阀门粘滞检测结果，部分结果如表5 所示。

对于该案例中采集到的360 个样本，本文提出的阀门粘滞检测算法成功地分类了其中的305个样本，准确率为84.7%。

3.2 数据案例2

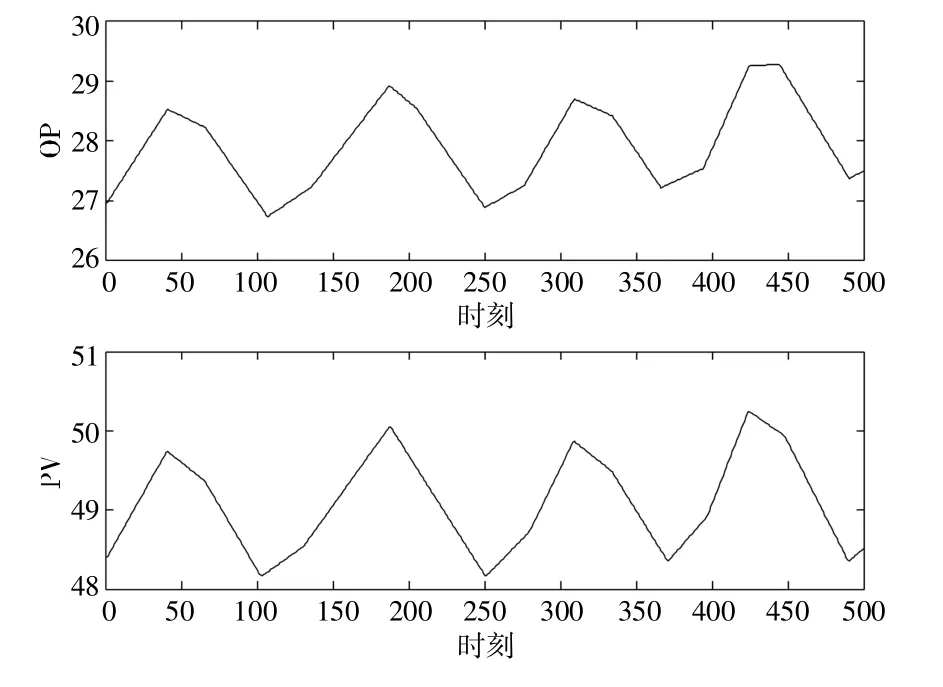
图5 密封水控制回路的OP 及PV 数据

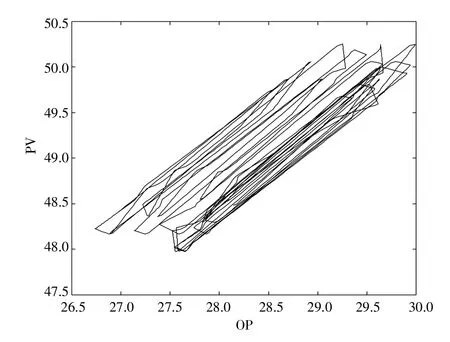
图6 密封水控制回路的OP-PV 图

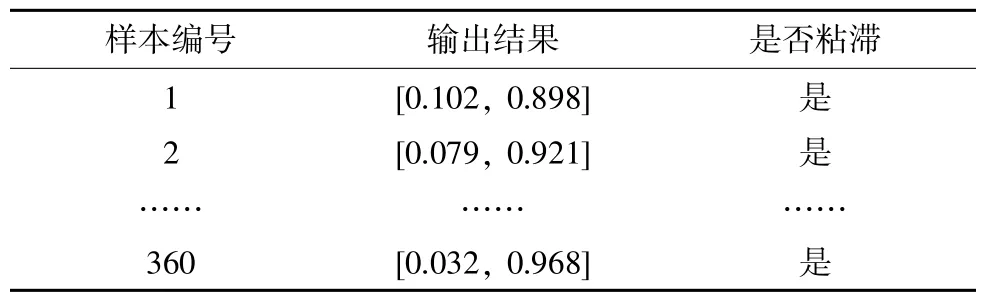
表5 阀门粘滞检测结果展示

本案例数据来源于文献[28]中提供的阀门粘滞公开数据集，为了方便与之前的方法进行对比，从其中选取了78 条标签准确的回路用作算法的测试集，这些回路数据来源于不同种类的工厂，如发电厂、化工厂等。这78 条回路中，有36条的标签为粘滞，剩余的42 条标签为非粘滞。在进行测试时，仅选择每条回路中前500 个数据点作为该回路的代表样本，用在该样本上的结果代表整个回路的检测结果。数据集中的CHEM29 回路的代表样本的OP 和PV 变量如图7 所示，图8为对应OP-PV 图。

本文所提方法在36 条粘滞回路上检测的准确率为24/36（66.7%），在42 条非粘滞回路上检测的准确率为33/42（78.6%），总体检测的准确率为57/78（73.1%）。该方法与部分已发表方法在该公开数据集上的对比结果如表6 所示。

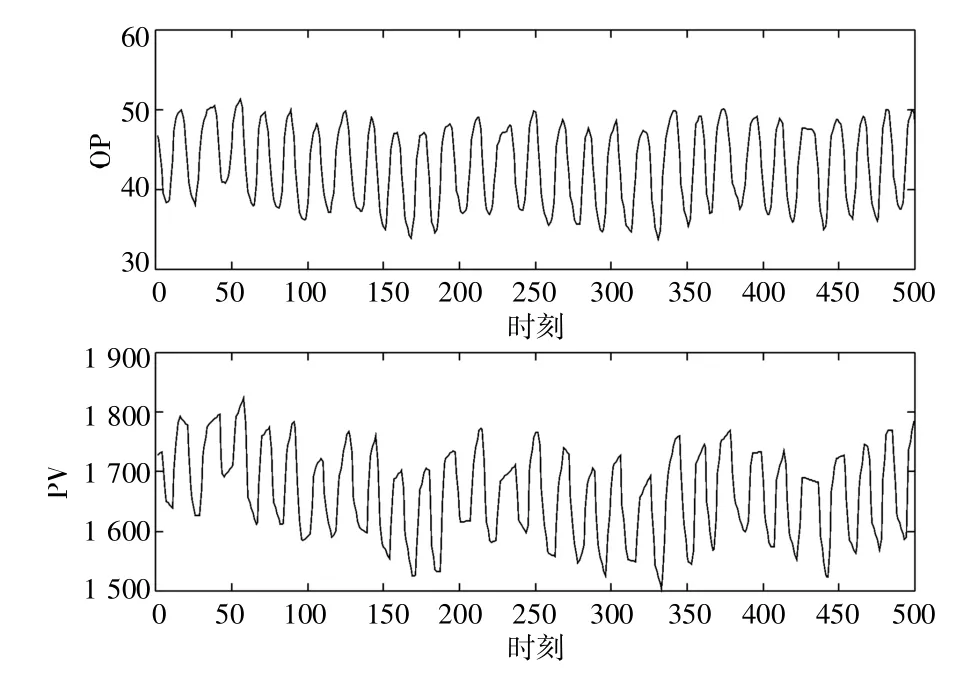
图7 回路CHEM29 的OP 及PV 数据

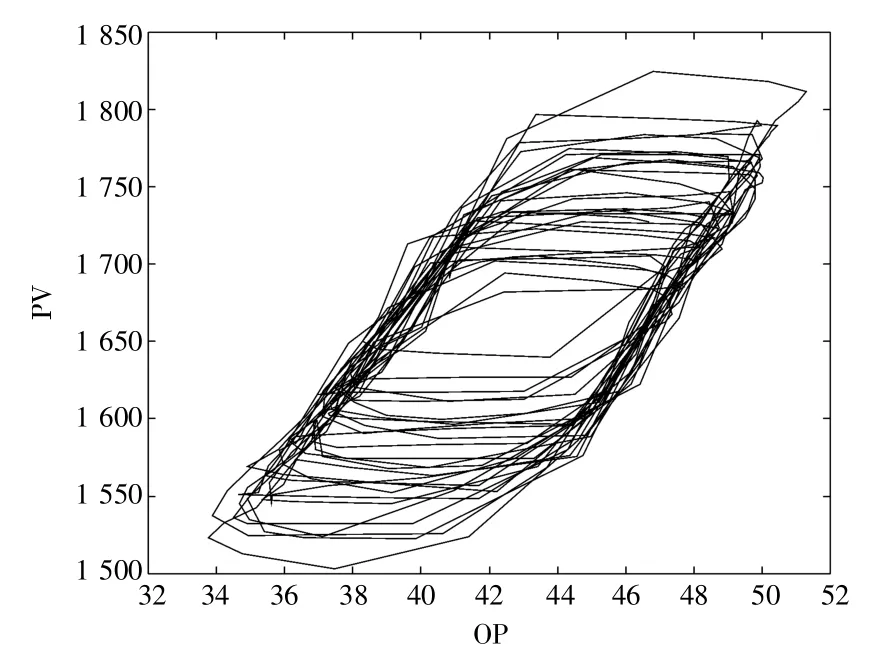
图8 回路CHEM29 的OP-PV 图

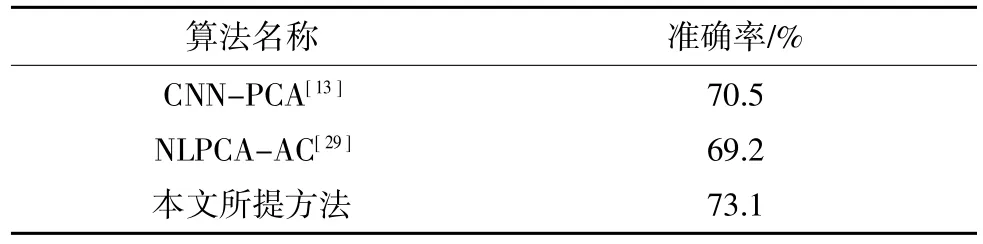
表6 阀门粘滞检测结果

通过不同方法间的对比可以看到，本文所提的方法相较于文献[16]和[29]中的算法在公开数据集上取得了更好的阀门粘滞检测结果。

4 结语

本文针对控制回路中的阀门粘滞检测问题提出了一种基于全卷积网络的检测方法。相比于其他的阀门粘滞检测方法，该方法减少了对于人工提取特征的需求，只需使用回路原始的控制变量以及过程变量数据就可以实现阀门粘滞检测，并且具有更加准确的检测结果。

训练集的质量对于深度学习中网络模型的精度有明显影响，在后续工作中，可以考虑生成更加丰富的仿真数据作为训练集。除此之外，还可以考虑结合迁移学习方法，将使用仿真数据训练得到的网络迁移到实际应用的回路中。