步进电机的模糊控制研究

（广东电网公司东莞供电局，广东 东莞 523000）

0 引言

伺服电动机或者步进电动机的共同点是提供了相似的精确定位，但是它们在许多方面又有所不同。伺服电动机需要模拟反馈控制系统，只能应用于闭环回路。而步进电机可用于简单的开环控制系统中。这些通常适用于在静态负载下以低加速度运行的系统，但是对于高加速度而言，尤其是在涉及可变负载的情况下，闭环控制是必不可少的[1]。

在本文中，提出了利用模糊控制逻辑的方法来控制步进电机速度。Zadeh[2]提出闭环控制方案采用的是将设计人员的经验与工程知识整合到自动控制系统中以描述复杂的系统。但是这些系统很难使用传统的数学方法进行分析。实际上，Mamdani[3]是第一个设计出模糊逻辑在实验室小型蒸汽机中的应用。这项研究的成功使许多科学家尝试使用模糊算法来控制过程，例如化学反应堆，自动电机或核反应堆的控制过程[4-5]。这些实验的结果表明，模糊控制器比传统控制器的性能更好。而且，该技术的优点是仅需一个简单的数学模型即可实现算法，该数学模型可通过数字计算机轻松实现。传统的控制方法在工业环境中应用广泛，但对于大滞后、非线性复杂的系统，传统常规控制方法的不稳定性导致控制效果并不理想。模糊控制不需要控制对象的精确数学模型，它是一种基于规则的控制，更多的是依据操作人员的控制经验，通过查表等方法，可以得到控制量，控制效果明显。另外，模糊逻辑被研究者更频繁地应用于控制电机，例如直流电动机或感应电动机[6]。然而，模糊逻辑的问题是它没有专门用于模糊控制器设计的系统程序。正是由于这个原因，在本文中提出使用ANFIS（自适应神经模糊推理系统）的方法[7-8]来调整模糊系统的参数，从而达到对系统进行控制的目的[9]。当然，还有其他混合方法可用于获得模糊系统[10]，但是，ANFIS是实现步进电机控制过程中所需要的精度和效率的理想选择。

1 步进电机的分类

步进电动机分为永磁体和可变磁阻2 种类型，可变磁阻电动机通常有3 个（有时是4 个）绕组，并具有相同的回路，而永磁电动机通常具有2 个独立的绕组，有的永磁电动机还具有中心抽头。中心抽头绕组用于单极永磁电动机[11]。步进电机具有多种角度分辨率。

1.1 可变磁阻电动机

如果电动机具有3 个绕组，如图1 所示。图中所有绕组共有一个端子，则该电机为可变磁阻步进电动机。在使用的过程中，公共线通常与电源正极连接，并且绕组依次通电。图1 所示的截面为可变磁阻电动机的横截面。该电动机有4 个转子，6 个定子，每个绕组都缠绕在2 个相对的磁极上。在给1 号绕组通电后，标记为X 的转子齿被吸引到该绕组的磁极上。如果关闭通过绕组1 的电流而打开绕组2 的电流，则转子将顺时针旋转30°，以使标记为Y 的磁极与标记为2 的极对齐。

图1 可变磁阻电动机

1.2 单极电机

如图2 所示，单极步进电机（包括永磁体电机和5 或6 线混合步进电机）通常为2 个绕组都有一个中心抽头。在使用过程中，绕组的中心抽头通常与电源正极相连，每个绕组的两端交替接地，其目的是为了将绕组提供的磁场方向进行翻转。图2 中所示的电动机横截面为30°每步的永磁电动机。对于具有更高角度分辨率的电机，其转子必须按比例具有更多的磁极与之相对应。图2 中的30°步进电动机是最常见的永磁电动机设计之一，尽管15°和7.5°每步的步进电动机也被广泛地使用。

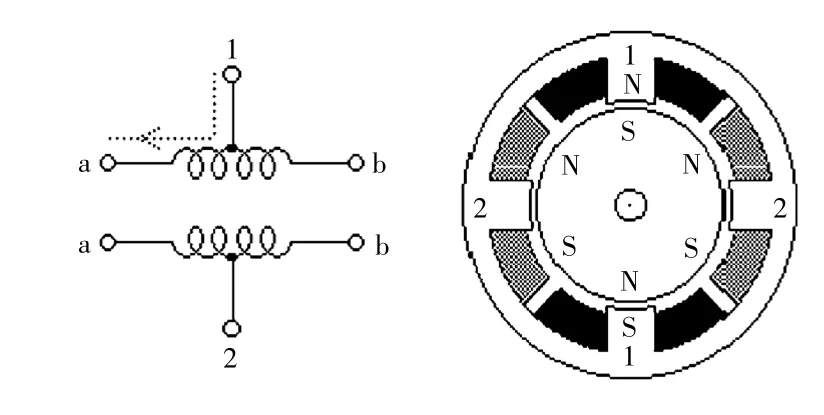
图2 单相电机

1.3 双极电机

双极永磁体和混合动力电动机的结构与单极电动机完全相同，但是2 个绕组的接线方式更加简单并且没有中心抽头。图3 显示了这种电动机的接线方式，电动机横截面与图2 的横截面完全相同。

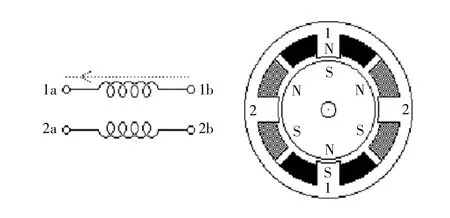
图3 双极电机

2 步进电机的动力学

每次步进电动机转动时，都要以电子的方式平移S 弧度。如图4 所示，这会将整个曲线移动了S 弧度的距离。

当转子从图4 中的一个步骤到另一个步骤的一半时，最大可用转矩达到最小值。该最小值是用来确定运行转矩，即确定电动机缓慢前进时可以驱动的最大转矩。如果通过一次给2 个绕组供电来驱动步进电动机，则理想的两绕组永磁电动机的运行转矩将与单绕组转矩保持一致。

电机转子的共振频率取决于振荡的幅度。但是，随着振幅的降低，谐振频率上升到小振幅频率。形式上，小幅度共振可以计算得到。首先，根据牛顿定律的角加速度可以得到：

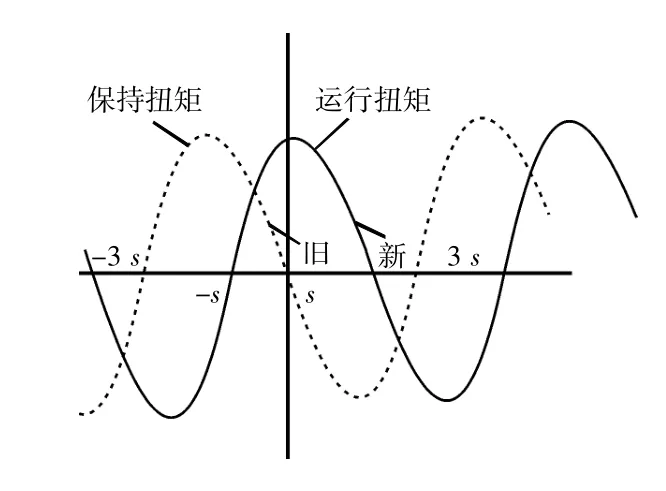
图4 步进电机的动力学

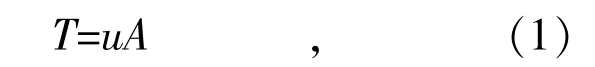
式中：T 为施加在转子的转矩；u 为转子和负载的惯性矩；A 表示为角速度，A 以弧度每秒为单位。假设对于小振幅，转子上的转矩可以近似地表示为从平衡位置开始位移的线性函数，即：

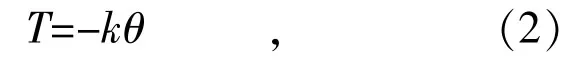
式中：k 为系统的弹簧常数，单位为每弧度的扭矩；θ 为转子的角位置，以弧度为单位。

将获得扭矩的2 个公式等价：uA=-kθ。加速度是位置相对于时间的二阶导数：。因此，可以用微分方程形式将其转换下形式为：。由f（t）=asinbt 得：

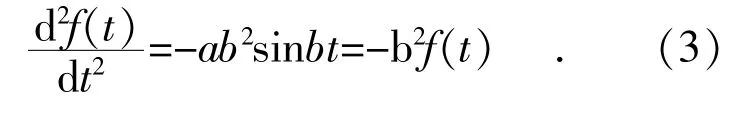
假设转子共振，因此是在谐振的过程中，具有如下运动方程：

式中：a 为表示共振角幅度；f 为共振频率。

实际上，当步进速率接近系统的谐振频率时，这种振荡会引起严重的问题。产生的后果为不可控制且随机出现。

3 步进电机的模糊逻辑控制

模糊逻辑控制器提供了一种算法，可以将基于专业知识的语言控制转换为自动控制策略从而达到控制电机运转的目的[12]。

根据实际数据，应用ANFIS 方法来调整模糊控制器的参数[13-14]。PC 中会把生成步骤输入到系统中并存储。模糊控制器也包含在PC 中，并进行相应的响应。实验系统如图5 所示。

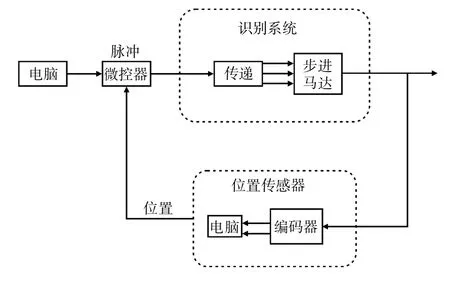
图5 实验系统

（1）电动机/驱动器

微步电动机型号为Vexta PV266-01E，具有5 个相数和500 步旋转。电机如图6 所示。具有多种分辨率的电源驱动器Vexta DFR1514A（最低：500 步；最高：125 000 步）。

图6 Vexta PV266-01E 步进电机

（2）数据采集卡

采用研华PCL-818，具有8 个模拟输入和2个模拟输出（12 位），16 个数字输入，16 个数字输出，采样时间为0.25 ms。

（3）计算机/软件

控制规则如下：

用于控制步进电机的Sugeno 模糊模型[15]。本文使用了ANFIS 方法来估计隶属函数及其后继函数的参数。对于每个语言变量，使用具有9 个规则和3 个隶属函数的模糊模型。如图7 所示，ANFIS 模糊系统的结构，同时利用ANFIS 方法构造显示自动设配网络中的模糊控制，由ANFIS 方法生成的模糊规则如图8 所示。这些规则是使用ANFIS 方法自动生成的。该模糊模型的非线性面如图9 所示。

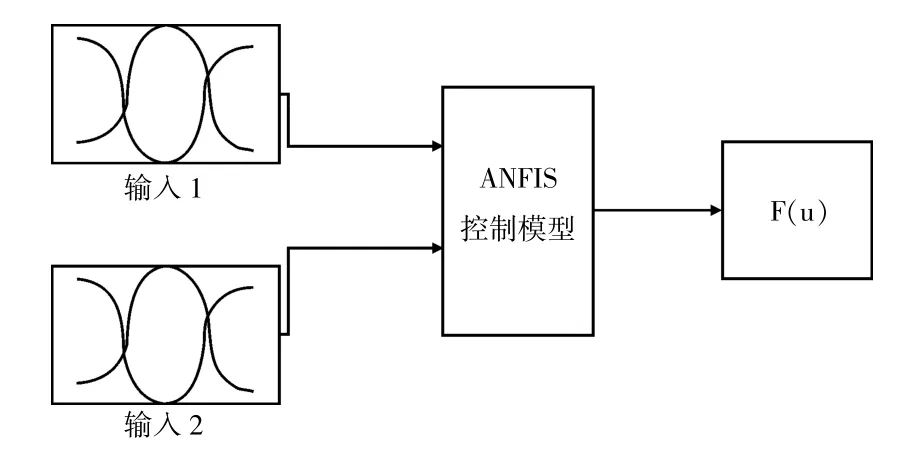
图7 ANFIS 模糊系统的结构

图8 由ANFIS 方法生成的模糊规则

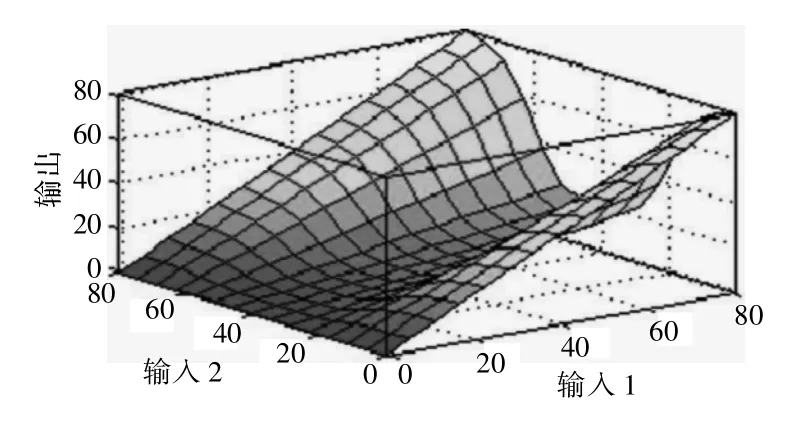
图9 Sugeno 模糊模型的非线性表面

4 硬件的实现

模糊控制需要ANFIS 控制器才能真正实现智能步进电机的目标。神经模糊方法使电动机具备了适应环境变化的能力。配备有智能控制器的步进电机将能够使用新数据对其进行训练，并进行数据参数的更新，从而能够相应地更改其行为。

ANFIS 方法的基础训练是在自适应网络上进行的，使用问题相关变量的时间序列作为数据。因此，选择了Jstamp 微处理器作为控制器的核心。该微处理器使用JAVA 作为本机编程语言，具有512 KB 的RAM 内存和512 KB 的FLASH内存。如图10 所示，为研究过程中的Jstamp 微处理器。由ANFIS 的数字混合性质可知，在正向使用最小二乘法，而反向传播算法是反向算法[16]。这些方法是用JAVA 语言实现的，然后将它们下载到Jstamp 微处理器中以获得模糊控制器。

图10 用于实现的Jstamp 微处理器

5 实验结果

如图11 所示，表示为步进电机对一系列步进输入信号的响应（本方案使用了400 个样本）。由图12 可得到ANFIS 方法应用于训练数据和测试数据的结果。使用了20 个纪元进行训练，最终误差为0.000 001，这对于此应用程序非常有用。

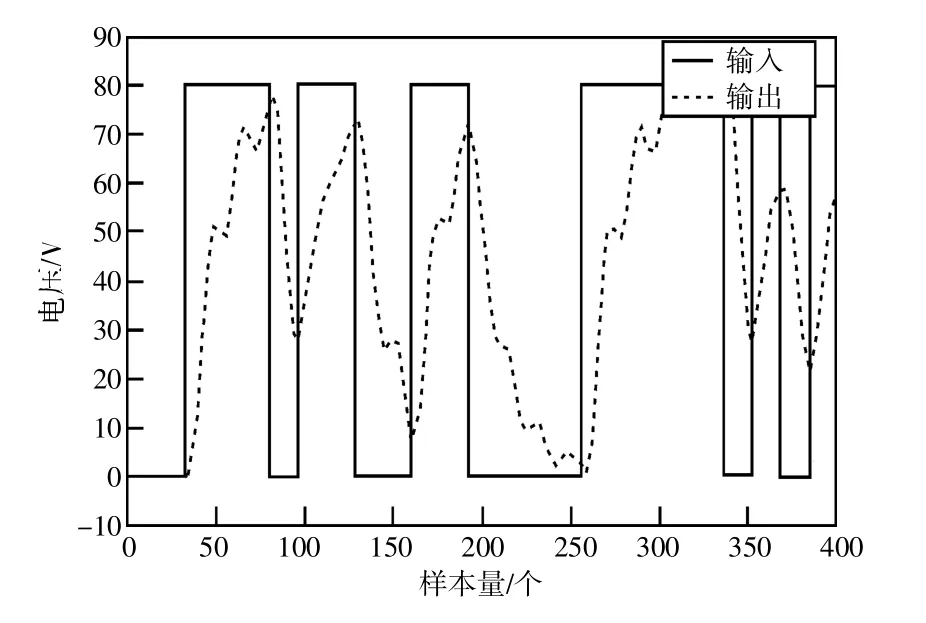
图11 步进电机对一系列步进输入信号的响应

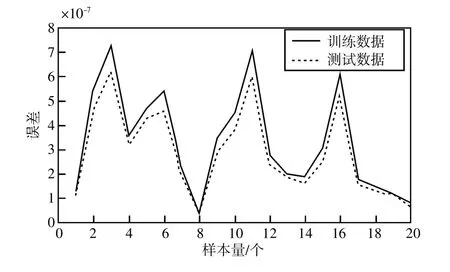
图12 将ANFIS 方法应用于训练和测试数据的结果

因此，所提出的设计证实了模糊控制与非线性过程的快速控制有关，例如步进电机驱动器中的定量方法并不总是合适的。与传统的定量控制器相比，该方法的另一个优点是不需要固定的采样时间。

6 结语

本文通过仿真和实验证明了模糊控制在步进电机驱动中的可行性。通过使用ANFIS 确定了模糊控制器的最佳参数。模糊控制器具有非常强大的跟踪功能，并且能够响应不同的动态条件，模糊模型产生的数据非常接近实际值。