基于非同步dq 坐标变换的电压暂降快速检测方法

郭建龙，刘善伟，刘文泽，吕梁景

（1.广东电网有限责任公司中山供电局，广东 中山 528437；2.启迪中电智慧能源科技（深圳）有限公司，广东 深圳 518000）

0 引言

随着分布式电源、非线性负荷在配电网的渗透率越来越高，电能质量问题日渐受关注，而电压暂降则是目前影响最大的电能质量问题[1-2]。电压暂降的检测算法是最基础的研究内容[3]，快速、准确地对受现场干扰严重的电压暂降信号进行检测，具有重要的研究意义和工程实用价值。

近年来，电压暂降检测方法研究取得了一系列成果，先后提出了基于小波变换的方法[4-5]、基于数学形态学的方法[6-7]、基于Hilbert 变换的方法[8-9]、基于S 变换的方法[10-11]。小波变换方法的基本原理是基于时频域信号特征提取来实现扰动信号量的检测，但在将检测信号进行多次时频域划分后，各频域的采样率逐次下降，信号开始失真，且扰动特征量受干扰信号的影响逐步加大，所以普遍存在特征量易受噪声影响、计算量大的缺点。数学形态学的原理是通过形态算子来检测信号边沿变化特征，实现扰动信号量的检测。但针对不同的扰动信号，不同的形态算子性能各异，无法用一种形态算子进行多种电压暂降的检测，因此本质上存在形态算子选择困难，以及算子组合适应性不高、易受干扰信号影响等缺陷。而Hilbert 变换本质上是一个移相器，其存在适用于窄带信号、处理单一频率等约束，对于任意给定t 时刻，通过希尔伯特变换运算后的结果只能存在一个频率值，即只能处理任何时刻为单一频率的信号。所以在具体算法设计中，Hilbert 变换需要和其他方法组合起来使用，存在计算量非常大的问题。基于S 变换的方法重点是信号消噪问题，但对于计算量大、多种电能质量信号叠加的问题并没有针对性。总体而言，这些方法存在计算量大、特征提取受干扰影响大等问题。

此外，还有不少学者提出了基于αβ 变换或dq 变换计算电压暂降特征量的方法[12-14]，以降低计算量。但这类方法对同步采样的要求比较高，一旦信号采样过程受干扰而导致锁相不成功、延时等，或者检测点过零易受干扰影响，都会存在检测精度不高等问题。故此这类方法在受噪声、频率偏移等常见干扰信号情况下，同步采样性能和电压暂降检测精度均大受影响。此外，这类算法仍存在计算量大的问题。

鉴于上述方法存在依赖同步采样、检测计算量大、受干扰影响等问题，本文基于坐标变换原理设计了一种不受同步采样失效影响的坐标变换方法，从本质上解决锁相的技术问题；并设计了参数自适应变化，可对噪声、频率偏移、幅值波动的影响进行处理的滤波器，从而达到提高检测精度的设计目的。

1 幅值和相位检测基本原理

以单相电压为例，其表达式为：

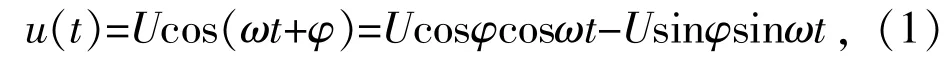
式中：U 为电压有效值；ω 为基波角频率；φ 为相角。

显然sinωt 和cosωt 是与u（t）同相位的正、余弦信号。而u（t）经过dq 变换，可获得d，q 两个分量：

对式（2）、式（3）求取半波平均值，可求得基波信号的幅值和相位（相当于d，q 分量的平均值）。具体公式为：

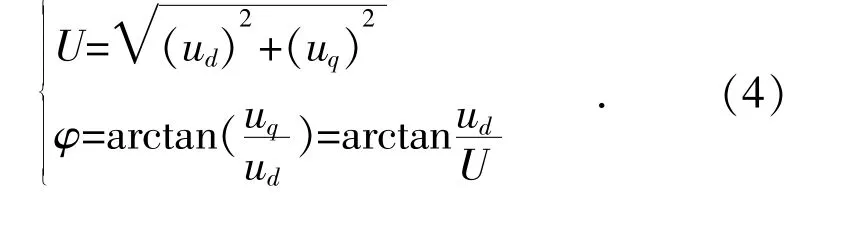
2 基于电压变换的电压暂降检测原理

将式（1）进行离散化，可得：

式中：T 为采样周期；n 为离散化后的采样点。

利用基波（ω50=50 Hz）正、余弦信号对式（5）分别进行正交变换，可得：

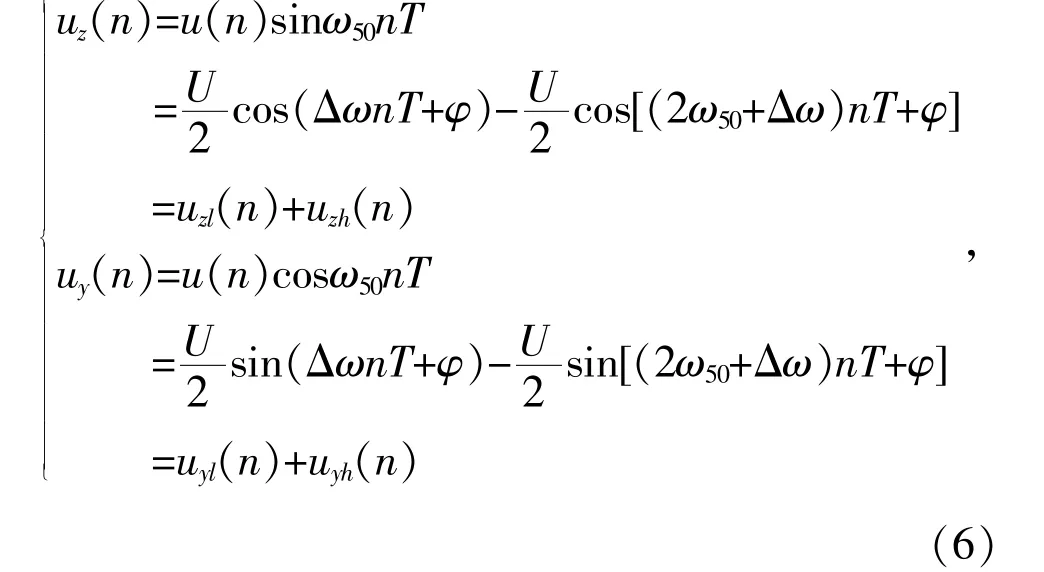
式中：Δω=（ω-ω50）为信号的瞬时频率差；uzl（n）和uzh（n）分别为uz（n）的低频信号（频率为Δf=Δω/2π）和解调分量（2ω50+Δω）；uyl（n）和uyh（n）分别为uy（n）的低频信号（频率为Δf=Δω/2π）和解调分量（2ω50+Δω）。

选择合适的低通滤波器，可以将公式（6）的高频信号过滤掉，从而获得低频分量uzl（n）和uyl（n），进而求出基波电压的幅值和相位：

可见，用基波正、余弦信号对电压采样信号进行分解可准确得到其幅值和相位。

在实际应用中，电网的频率并不是恒定值，频率偏移、相位跳变等影响会导致相位偏差的出现。如下式所示：

式中：Δφ 为相位跳变；Δωi为瞬时角速度与ω50的差值。

由于实际电力系统运行时的频率一般维持在（50±0.5）Hz 范围内，因此Δωi一般在[-π，π]范围内波动。通过式（7）可判断电压暂降发生时刻和结束时刻。因此，在暂降发生前或暂降持续过程中取k 个采样间隔，则由频率偏差引起的相位平均偏差为：

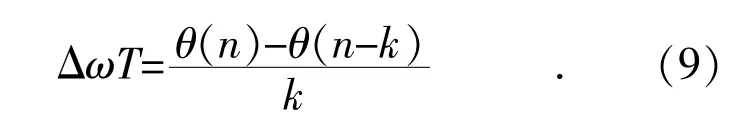
假设当被测电压信号突然发生相位跳变为Δφ 的电压暂降，同时伴随Δω 的频率偏移。观察式（6）可知，uz（n）和uy（n）本身就是正交坐标系，令uα=uz和uβ=uy，将αβ 静止坐标系中的uα和uβ进行坐标变换，可得：

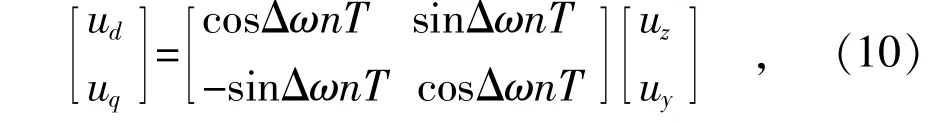
式中：n 为当前检测点和初始相位的偏移量；ΔωT为暂降持续过程中由于频率偏差引起的一个采样周期的相位偏差量。

将式（6）代入式（10），可得到dq 旋转坐标系上的两个分量ud和uq，继而得到电压的相位跳变计算公式：

上述分析中，电压变换检测算法采用基波频率进行采样信号的幅值和相位计算。其优势在于：可以不依赖于锁相环技术；可以应对频率偏移和相位跳变的影响。

3 参数自适应滑动平均滤波器

由前文分析可知，低通滤波器的性能非常重要，其影响在于滤波器延时时间和滤波器滤波性能。为实现将（2ω0+Δω）分量进行较好的滤波，本文选用MAF（滑动平均滤波器）[15]。

MAF 的表达式为：

由式（12）可知，MAF 的滤波性能受到其窗口宽度Tω大小的影响，即MAF 的准确输出需要周期为Tω的时间积累数据。

经过离散化后MAF 频率响应特性为：

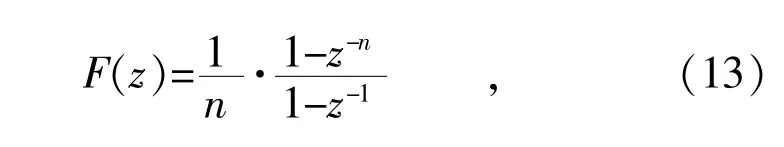
式中：n 为采样点数，且n=fsTω（fs为采样频率）。

MAF 的传递函数可推导为：

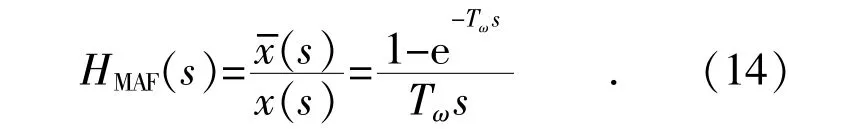
令s=jω，可以得到MAF 的幅频与相频特性：

由式（15）可知，当ωTω=2nπ（n=1，2，3，…）时，MAF 的幅值增益为0，此时可以完全将频率为（n/Tω）的信号滤去。

由于MAF 的输入信号是离散的，因此在使用过程中，将式（12）进行离散化可得：

式中：N 为MAF 的窗宽。

根据上述滤波原理可知，在信号频率发生变化时，滤波效果会受到固定的Tω的影响，因此，若要改善滤波效果，可以采用参数自适应MAF，即设计可随信号频率的波动而变化的Tω（而非固定不变的Tω）。一般有Tω=NTs，其中Ts为采样时间。由于Tω/Ts在大多数情况下并不是整数，需要对该比值采用四舍五入法取整，因此会不可避免地引入一定的误差。为表示误差大小，本文根据线性插值法，引入了加权因子α：

而

式中：floor（.）为向下取整函数。

将能够表示取整时小数部分的变量α 代入式（16）可得MAF 的离散化公式：

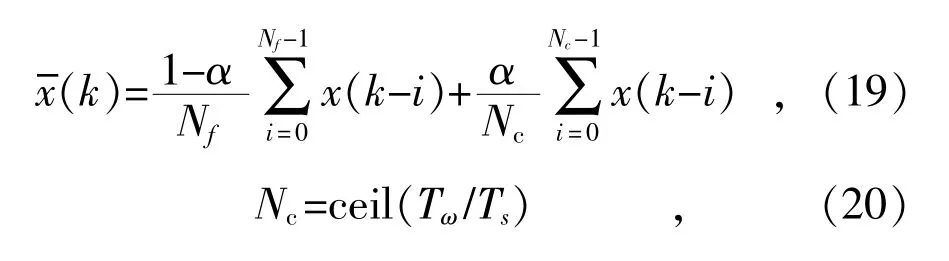
式中：ceil（.）为向上取整函数。

依据非同步采样检测算法原理，对低通滤波器参数自适应算法进行分析，当Tω=1/π（2ω0+Δω）时，不仅能够令滤波器有效地滤除（2ω0+Δω）分量，还可以保证算法具备较好的动态响应特性。

4 仿真分析

将本文方法与当前广泛应用的延时90°的αβ变换法、dq 变换法进行比较，利用MATLAB 进行仿真。

仿真中设定单相电压幅值为220 V，基波频率为50 Hz，信号的采样频率为12.8 kHz（每周期采样256 点）。考虑到实际电力系统往往伴有一定的谐波分量，且以奇次谐波为主，为验证谐波分量对检测结果的影响，在理想220 V 电压波形上叠加一定的谐波。本文采用MAF 作为低通滤波器，而αβ 变换法选用的是截止频率为100 Hz 的二阶巴特沃斯低通滤波器。

4.1 全程频率不变的仿真

此仿真过程：全程叠加10%的3 次谐波、5%的5 次谐波与3%的7 次谐波；在0.12 s 时发生暂降深度为50%、相位跳变角为30°的电压暂降，暂降持续时间为0.04 s；电压暂降期间频率不变。

由图1 可知：

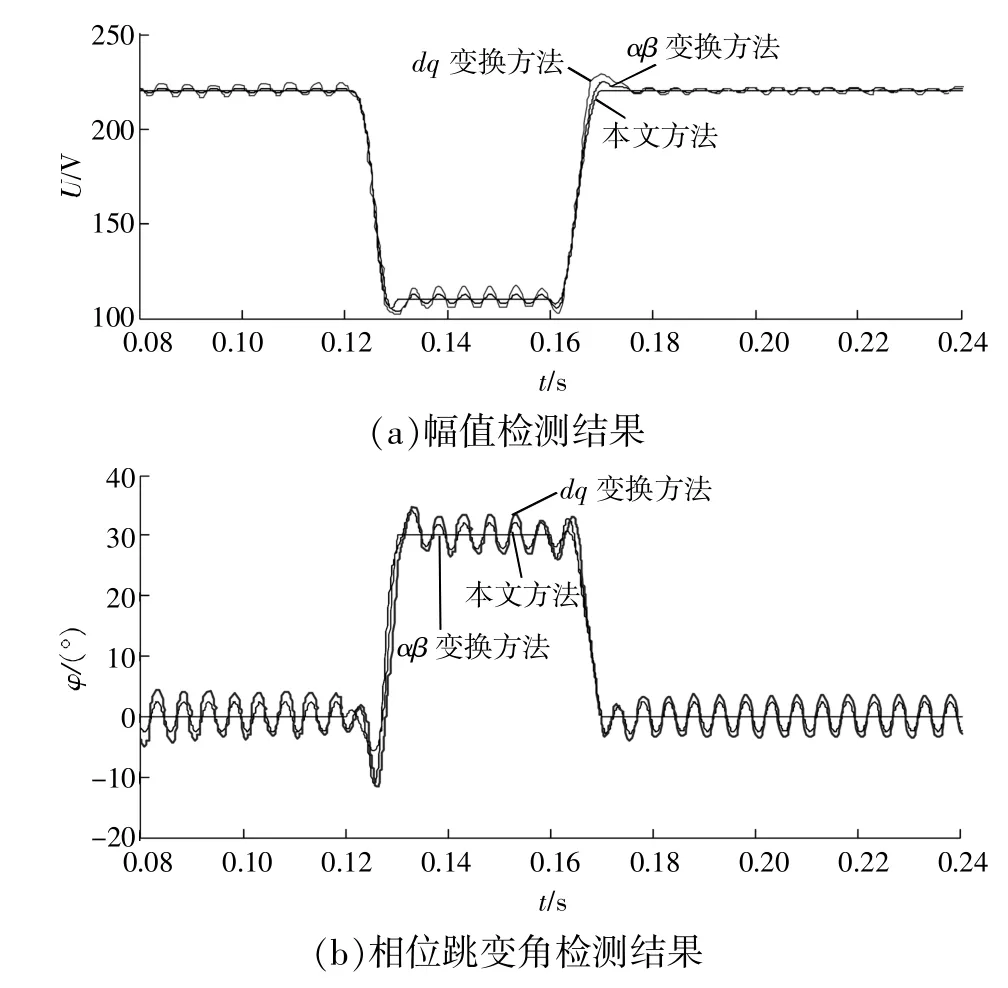
图1 系统频率不变时电压暂降检测结果

（1）由于无频率偏移的干扰，两种方法基本可以检测到电压暂降的起、止时间。

（2）由于h 次谐波经过αβ 变换法后会转换成h-1 次振荡信号的叠加，影响检测精度；dq 变换法也有类似问题；但利用MAF 可有效滤除由谐波引起的振荡信号，大大增加了检测精度。

（3）滤波器的延时作用使得两种方法的检测时间相近。

4.2 频率发生变换的仿真

此仿真过程：暂降前信号无谐波叠加，频率为50 Hz；发生暂降时，系统频率变为50.5 Hz，同时伴有10%的3 次谐波、5%的5 次谐波与3%的7 次谐波；而且电压暂降深度为50%，相位跳变角为30°，暂降持续时间为0.05 s；暂降结束后系统频率维持50.5 Hz，无谐波叠加。

由图2 可知：

图2 系统频率变化时电压暂降检测结果

（1）由于频率偏移的干扰，αβ 变换法的相位跳变角检测会产生明显误差，dq 变换法也有类似问题，而本文方法不受影响。

（2）对于谐波的干扰，本文方法仍能有效处理，而αβ 变换法、dq 变换法的结果失去了参考价值。

5 结语

针对现有算法高度依赖于同步采样、计算量大、受干扰影响大等问题，本文从算法设计与滤波器改进两方面开展研究，取得如下成果：

（1）设计了一种基于坐标变换的电压暂降快速检测方法，该算法利用αβ 变换或dq 变换进行信号处理后，可避免频率偏移和相位跳变的影响，从而达到不依赖于锁相环技术而能准确计算信号幅值和相位的目的。

（2）结合MAF 和电压暂降信号特征进行分析，针对离散化信号计算误差问题，利用加权因子进行处理，并设计可随信号频率的波动而变化的参数来实现自适应滤波。

（3）通过仿真分析，将本文方法与当前广泛应用的延时90°的αβ 变换法和dq 变换法进行比较，验证了本文所提方法的有效性。