我国上市商业银行系统性风险溢出效应研究——基于GARCH-Copula-CoVaR模型

1 研究背景和意义

Bernanke（1983）认为，金融机构倒闭会造成实体经济下滑，受其影响其他金融机构也会偏向于保留流动性强的资产，这可能会造成其收益性降低，从而体现了金融机构的风险溢出效应。Allen and Gale(2000)指出风险产生和传导的根本原因是金融业之间相似的网络结构，机构之间的网络结构越相似，其系统越脆弱，其风险溢出效应越大。在国内，包全永（2005）分别研究了开放和封闭系统下银行系统性风险的传导机理，说明了银行系统性风险具有溢出性。肖璞（2012）认为单个银行的风险扩散便是风险溢出效应，对于具有较强风险溢出效应的银行，其倒闭会导致银行体系爆发系统性风险。Adrian和Brunnermeier(2011)在Var模型的基础上构建了CoVar模型，这种方法可以用来衡量整个金融体系的风险溢出程度，用CoVaR可以衡量出当金融机构i发生波动时，金融机构j相应的风险增加值。

2 商业银行系统性风险溢出效应的理论分析

2.1 商业银行系统性风险溢出效应的定义

银行系统性风险的界定标准主要分为两部分：一部分是风险传播途径，另一部分是其负外部性。从风险传播途径来讲，当某一银行受到实际业务的影响出现流动性危机，继而通过信息传播，造成挤提的发生，一旦该银行失败，就会大大增加银行的系统性风险；当整个银行体系受到总冲击影响时，由于信息的传播，存款者认为一些资产状况好的银行会与资产状况差的银行一样，从而导致资产状况好的银行也出现挤提，造成恐慌，从而增加银行的系统性风险。从负外部性来讲，外部性是指一个人或者一群人的行动和决策使另一个人或另一群人受损或者受益的情况；负外部性是指受损的情况，当商业银行在实施某些业务或者采取某些措施时，通常只会考虑自身的利益，而忽略对整个银行体系造成的影响，从而产生负外部性的影响。

本文将商业银行的系统性风险溢出效应定义为：由于银行体系中商业银行的密切相关性，当某一银行处于一般或极端风险状况时，由于风险的负外部性给整个体系以及体系中其他银行所带来的负面效应，即银行体系中某一部分的失败造成体系中其他部分失败的可能性。也即在银行体系中，当某一银行遭受损失时，对与之相联系的其他银行造成的损失。

2.2 银行系统性风险的特征

2.2.1 传染性

传染性特征是系统性风险的一个基本特征。从金融渠道来看，其一是金融机构间的传导，由于金融机构间错综复杂的业务交往导致资产负债的风险传导；其二是由于利率的变动、汇率的变化等外部因素的影响所诱发的风险传导。从投资者预期渠道来看，若某一单一市场出现危机，投资者会出现恐慌心理，从而做出冲动决策，如将其全部资金从该市场及与之联系微弱的其他市场抽逃，加之羊群效应，加剧了此风险传导的影响。

2.2.2 违约性

违约的系统性风险主要是因为银行持有资产下降而引起的，导致银行资不抵债。银行资产主要分为外部资产和银行间资产两种类型。外部资产主要是指银行持有的非金融部门的业务；银行间资产主要指该银行对其他银行的资产所有权，如同业存贷款。当债券面临违约风险、贷款成为不良贷款或者由于外界因素导致资产贬值等情况出现时，银行的持有资产都会遭受一定程度的缩水。而银行的净资产指的是银行间资产除去银行间负债的部分。当银行资产出现缩水时，首先会被银行的净资产所吸收，但是当净资产也为0之后，银行就会因为其负债出现违约。当某一银行对另一银行的违约达到某一程度后，由于其传导性，另一银行也会出现资不抵债的情况，对其负债进行违约，如果按照这种方式一直传递下去就会造成违约的系统性风险。

3 风险溢出与GARCH-Copula-CoVaR技术

3.1 ARMA-GARCH模型

3.1.1 ARMA模型

自回归滑动平均（ARMA）模型表达式为：Yt=μ+β1Yt-1+β2Yt-2+…+βpYt-p-θ1εt-1-θ2εt-2…-θqεt-q+εt。{εt}是白噪声序列，序列中的每个观测值是用过去的p个观测值和q个残差的线性组合来表示。常数项为μ，一般要求移动平均多项式与自回归部分多项式无公因子，否则在上式两边消去一个公因子，方程所决定的过程就变成了一个白噪声序列。ARMA模型在金融中的应用与波动率建模密切相关。

3.1.2 GARCH模型

首先提出的是自回归条件异方差（ARCH）模型。ARCH（q）模型的一般形式为：

其中vt为均值0，方差为1的独立同分布的白噪声过程，并且α0＞0,αj≥0,j=1,…,q,α1+α2+…+αq＜1,系数αi必须保证εt的无条件方差是有限的。在实际应用中我们通常假设{vt}服从标准正态分布，标准化t分布或广义误差分布。在ARCH模型的基础上，又进一步提出了广义的ARCH模型，也就是GARCH模型。

3.2 常见的Copula函数的参数估计法

对Copula函数进行参数估计，比较常见的方法有以下三种：EML估计法、IFM估计法和CML估计法。

(1)EML估计法

EML估计法又被称作极大似然估计法，设随机变量X1、X2的Copula函数为C(u1,u2),密度函数为c(u1,u2)，边缘密度函数为，已知；。

联合分布的密度函数为：

由此可以得到函数的对数似然函数为：

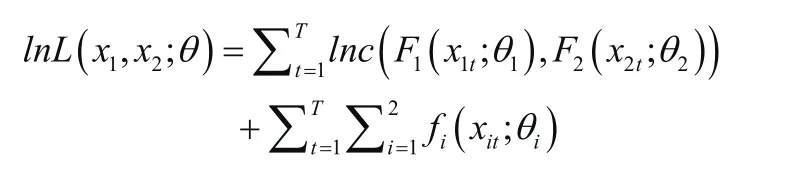
(2)IFM估计法

第二步，利用极大似然估计法估计出Copula中的参数，即

(3)CML估计法

第一步，首先将经验分布函数的样本数据{x1t,x2t…,xnt},t=1,2,…T转换为服从与均匀分布的均匀变量{z1t,z2t…,znt},t=1,2,…T,zit=Fi(xit)。

第二步，利用极大似然估计法估计出Copula函数的未知参数。

3.3 GARCH-Copula-CoVaR模型

本文利用二元Copula函数进行建模分析。根据Sklar定理，存在一个二元Copula函数C，使得随机变量（X，Y）的联合分布函数为下式所示：Fxy(x,y)=Pr(X≤x,Y≤y)=C(FX(X),FY(Y)),其中FXY表示边缘分布函数为FX和FY的联合分布函数。对于连续的FX和FY，C是由唯一确定的，其中随机变量u=FX(X)和v=FY(Y)为均匀分布。

由于在利用EML估计参数时，因为同时估计边际分布和Copula参数，计算量比较大，运行起来较为复杂，本文主要采用IFM方法对参数进行估计。

我们将金融机构的收益率定义为Rt=(Ri,t,Rs,t)，t=1,2,…，T，当边缘分布函数与Copula函数均为连续型函数时，Copula联合密度函数为：

其中θ是Copula参数，φi和φs分别为Ri,t和Rs,t边缘分布函数的参数，ut=FRi,t(Ri,t;φi),vt=FRs,t(Rs,t;φs),极大似然函数可表示为：

观察等式的右边我们发现其主要由两部分构成，一部分只包含Copula函数的参数θ，另一部分只包含边缘分布的参数φ，所以，我们首先为收益率序列构建合适的边缘分布，然后在拟合得到合适的Copula函数，最后估计得到Copula参数。