基于NSGA2遗传算法的地铁隧道上方基坑工程优化设计

卜康正，赵勇，郑先昌

基于NSGA2遗传算法的地铁隧道上方基坑工程优化设计

卜康正1，赵勇2，郑先昌3

(1. 深圳市水务规划设计院股份有限公司，广东 深圳 518000；2. 中铁南方投资集团有限公司，广东 深圳 518052；3. 广州大学 土木工程学院，广东 广州 510006)

为在有效控制基坑下覆地铁隧道竖向位移的情况下，尽可能地减小基坑工程造价，基于NSGA2遗传算法，以5个基坑工程控制下覆地铁隧道竖向位移的关键设计参数为优化设计变量、隧道最大竖向位移和工程造价中的可变值为优化目标，优化得到Pareto最优解集。结合专家打分-COWA算子-博弈论组合赋权法和TOPSIS法从Pareto最优解集中选出最佳方案，并分析专家打分的主观权重改变对最佳方案的设计变量、目标函数值等参数的影响。研究结果表明：最佳方案比初始方案的隧道最大竖向位移减少23.3%，工程造价中的可变值减少36.9%，证明本文对地铁隧道上方基坑工程优化设计方法的有效性。

基坑工程；地铁隧道；竖向位移；工程造价；优化设计；NSGA2遗传算法

骑驾于城市地铁隧道之上的大面积基坑开挖引起地铁隧道周围土体应力释放，地铁隧道随之发生向上的竖向位移。若竖向位移过大，将会影响地铁隧道衬砌正常工作的应力状态和耐久性，危及地铁运行安全。但为适应我国城市大规模建设的需要，地铁隧道上方基坑工程大幅增加的趋势不可避免。因此，如何分析和优化设计地铁隧道上方的基坑工程以减少基坑开挖引起地铁隧道竖向位移成为了研究热点。曹顺等[1]通过数值模拟的方法，研究发现土方明挖卸载完成后，隧道竖向位移会随坑底暴露时间的增长而增加；魏纲[2]依托杭州市某地下道路基坑开挖实例，通过监测下覆隧道竖向位移，发现抗浮板的浇筑可到达保护隧道的目的；姚爱军等[3]利用实验与有限元模拟的手段，分析了土方明挖卸载引起下覆地铁隧道竖向位移的规律，分析结果表明土方明挖卸载完成后及时施作抗浮板有利于减少地铁隧道竖向位移；左自波等[4]依托上海市某地下道路基坑工程，对比了不同跳挖方法对保护下覆地铁隧道效果的优劣；林杭等[5]利用有限元模拟的手段，分析得到基坑沿隧道纵向长度、横向宽度、深度与下覆近接隧道竖向位移的关系曲线；曹前[6]依托长沙市某基坑工程，采用数值模拟的手段，得到基坑分小块开挖纵向长度、横向宽度的合理设计值。可见，这些研究都只针对基坑工程的单个参数进行单一变量分析和单独的优化设计，并不能同时对多个参数进行协同的优化设计。当多个参数都单独选取最优设计值时，极可能导致最终隧道竖向位移远小于规范的控制值和工程造价过高的问题。因此，对地铁隧道上方基坑工程进行协同的双(或多)目标优化设计具有重要意义。鉴于此，本文依托深圳市某待开挖的公路隧道基坑工程，以基坑开挖纵向分块个数、抗浮板厚度、抗拔桩实桩长度、抗拔桩直径、单侧抗拔桩个数等5个基坑工程控制下覆地铁隧道竖向位移的关键设计参数为优化设计变量，以隧道最大竖向位移、工程造价中的可变值为优化目标，利用NSGA2遗传算法优化得到Pareto最优解集；结合专家打分-COWA算子−博弈论组合赋权法和TOPSIS法对Pareto最优解集中的各个解进行评估并排序，并分析专家打分法的主观权重改变对最佳方案的设计变量、目标函数值等参数的影响。

1 基坑工程关键设计参数与下覆隧道最大竖向位移、工程造价的关系式求解

已知依托待放坡开挖的基坑坑顶纵向长为95.5 m，横向宽为52 m，深度为5 m，坡度为1.5，采用小竖井工法施工[7]；小竖井横向宽17 m，深5 m。小竖井的锁口圈梁截面高1 m，宽1.5 m。小竖井的锚杆支护长3 m，竖向间距0.5 m，水平间距1 m。采用Midas gts/NX对依托算例进行数值模拟，建立纵向长为300 m，横向宽为150 m的三维数值模型如图1所示，各土层参数见表1。

(a) 基坑开挖的整体模型；(b) 竖井、隧道与抗拔桩的位置概况

表1 各土层参数

由于隧道竖向位移大小变化是协同的，因此本文只选取左隧道竖向位移进行分析。而本文未优化的初始方案是由生产实践经验得到的。以基坑开挖纵向分块个数为13个、抗浮板厚度为1 m，抗拔桩实桩长度为15 m，抗拔桩直径为1 m，单侧抗拔桩个数为27个(即抗拔桩纵向间距为3 m)的初始方案下隧道最大竖向位移为基准，通过数值模拟对依托算例基坑参数进行影响性分析，分别得到不同的基坑开挖纵向分块个数、抗浮板厚度、抗拔桩实桩长度、抗拔桩直径、抗拔桩个数的条件下隧道最大竖向位移。利用matlab编程分别得到它们与初始方案下隧道最大竖向位移倍数关系的拟合多项式。再综合各个拟合多项式，得到与基坑开挖纵向分块个数1，抗浮板厚度2，抗拔桩实桩长度3，抗拔桩直径4，单侧抗拔桩个数5相关的隧道最大竖向位移拟合表达式为：

(1)

且按照暂行规范[8]规定：(1,2,3,4,5)＜20 mm。

针对地铁隧道上方基坑工程，特别是采用小竖井工法[7]的基坑工程，其工程造价表达式为：

工程造价=小竖井个数×(单个小竖井体积×相应的单价+单个小竖井的锁口圈梁体积×相应的单价+单个小竖井所需锚杆长度×相应的单价)+抗浮板厚度×抗浮板底面积×相应的单价+单侧抗拔桩个数×抗拔桩实桩长度×抗拔桩横截面积×相应的单价×2+单侧抗拔桩个数×抗拔桩空桩长度×抗拔桩横截面积×相应的单价×2+挖土方总价+整体大基坑支护总价

收集的经验数据：小竖井工程相应的单价约为400元/m3，小竖井的锁口圈梁工程相应的单价约为450元/m3，小竖井所需锚杆工程相应的单价约为75元/m，抗浮板相应的单价约为550元/m3，抗拔桩实桩工程相应的单价为900元/m3，抗拔桩空桩(成孔)工程相应的单价为200元/m3，设挖土方总价和整体大基坑支护总价为定值。

则代入变量——基坑开挖纵向分块个数1，抗浮板厚度2，抗拔桩实桩长度3，抗拔桩直径4，单侧抗拔桩个数5，可得地铁隧道上方基坑工程中工程造价可变值为：

本文地铁隧道上方基坑工程优化设计的目标是通过对基坑开挖纵向分块个数1，抗浮板厚度2，抗拔桩实桩长度3，抗拔桩直径4，单侧抗拔桩个数5共5个设计变量的合理取值，隧道最大竖向位移和工程造价可变部分达到最小，即：

2 地铁隧道上方基坑工程的双目标优化及决策过程

本文优化目标函数(1,2,3,4,5)和(1,2,3,4,5)不能同时达到最小，即没有使2个目标同时最优的解，只有均衡2个优化目标的Pareto最优解集。因此，地铁隧道上方基坑工程的优化设计可分为2个步骤：1) 求出Pareto最优解集；2)对比Pareto最优解集全部元素的评估结果，选出一个与最优水平(2个目标同时最优)最接近的最佳方案。

2.1 双目标优化

本文采用NSGA2遗传算法[9]进行优化，NSGA2遗传算法可有效解决非线性优化问题，突破了加权求和法、线性规划法、-约束法等传统多目标优化方法在缺乏经验的情况下效果不佳、甚至失效的瓶颈，其具体优化过程如图2所示。

图2 NSGA2遗传算法的优化过程

2.2 双目标决策

由于本文2个优化目标涉及到人为判断工程实操性和经济性的问题，需要考虑人的主观因素影响，因此需对2个优化目标重要性的大小进行主观评估，得到2个优化目标的主观权重。以2个优化目标为评估指标，基于Pareto最优解集，引入COWA算子[10−11]计算2个指标的客观权重，有效减弱Pareto最优解集中两端较不可靠的解对客观赋权的影响。再基于博弈论的思想[12−13]，协调、组合客观权重和主观权重，得到综合权重。最后，结合综合权重，采用TOPSIS法[14−15]对Pareto最优解集的各个解进行评估并排序。具体的决策计算过程：

1) 利用专家打分法计算2个指标的主观权重β(共有位专家)：

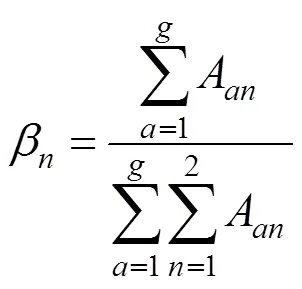
式中：A为第位专家对第个指标的打分值。

2) Pareto最优解集共有个解，将2个目标函数作为评估指标，可得到指标矩阵：

3) 标准化处理指标矩阵的各个元素：

式中：max为每列的最大元素。

4) 利用COWA算子计算2个指标的客观权 重ω：

5) 基于博弈论，利用2个线性组合系数组合客观权重和主观权重，并使得到的综合权重与客观权重、主观权重离差极小化。得到的综合权重ψ：

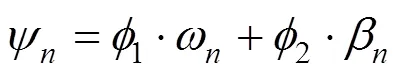
6) 对指标矩阵的各个元素进行赋权，得到赋权矩阵：

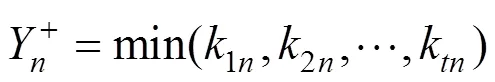
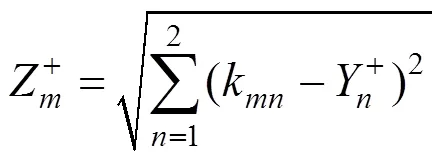
9) 计算得到Pareto最优解集中第个解与最优水平的接近指数R，并按降序排序(R越大，与最优水平越接近)：

3 优化及决策结果分析

3.1 优化结果

设定NSGA2遗传算法交叉概率为0.9，交叉分布指数为20，变异概率为0.1，变异分布指数为20，种群数量为200，迭代代数为500，利用matlab编程求出Pareto集结果如图3所示。

图3 Pareto最优解集结果

3.2 决策结果

10位专家对隧道最大竖向位移和工程造价中的可变值2个指标的重要性进行打分(不重要——1分，一般——2分，较重要——3分，重要——4分，很重要——5分)，打分情况见表2。

表2 专家对2个指标的打分

利用式(4)计算得到隧道最大竖向位移和工程造价中的可变值2个指标的主观权重分别为0.445 8，0.554 2。

利用式(7)计算得到隧道最大竖向位移和工程造价中的可变值2个指标的客观权重分别为0.609 8，0.390 2。

2个线性组合系数分别为0.661 3和0.338 7，则利用公式(8)计算得到2个指标的综合权重分别为0.554 3，0.445 7。

则利用TOPSIS法决策得到Pareto最优解集中次序前10的解见表3。

表3 决策得到Pareto最优解集中次序前10的解

图4 次序1的解在Pareto最优解集中的位置

将次序1的解作为本文地铁隧道上方基坑工程优化设计的最佳方案，该解在Pareto最优解集中的位置如图4所示。

将最佳方案与初始方案的决策结果进行对比，对比结果见表4。

由表4可知，最佳方案比初始方案的隧道最大竖向位移减少了23.3%，工程造价中的可变值减少了36.9%，与最优水平的接近指数增加了60.9%，证明本文对地铁隧道上方基坑工程的优化设计方法有效可行。

表4 最佳方案与初始方案的对比结果

4 主观权重对各因变量的影响分析

改变隧道最大竖向位移指标的主观权重依次为0，0.2，0.4，0.445 8(算例)，0.6，0.8和1，可分别得到不同的最佳方案。在隧道最大竖向位移指标的主观权重变化过程中，不同最佳方案中变量、目标函数值和前文算例最佳方案的次序号等因变量变化如图5(a)～5(h)所示。

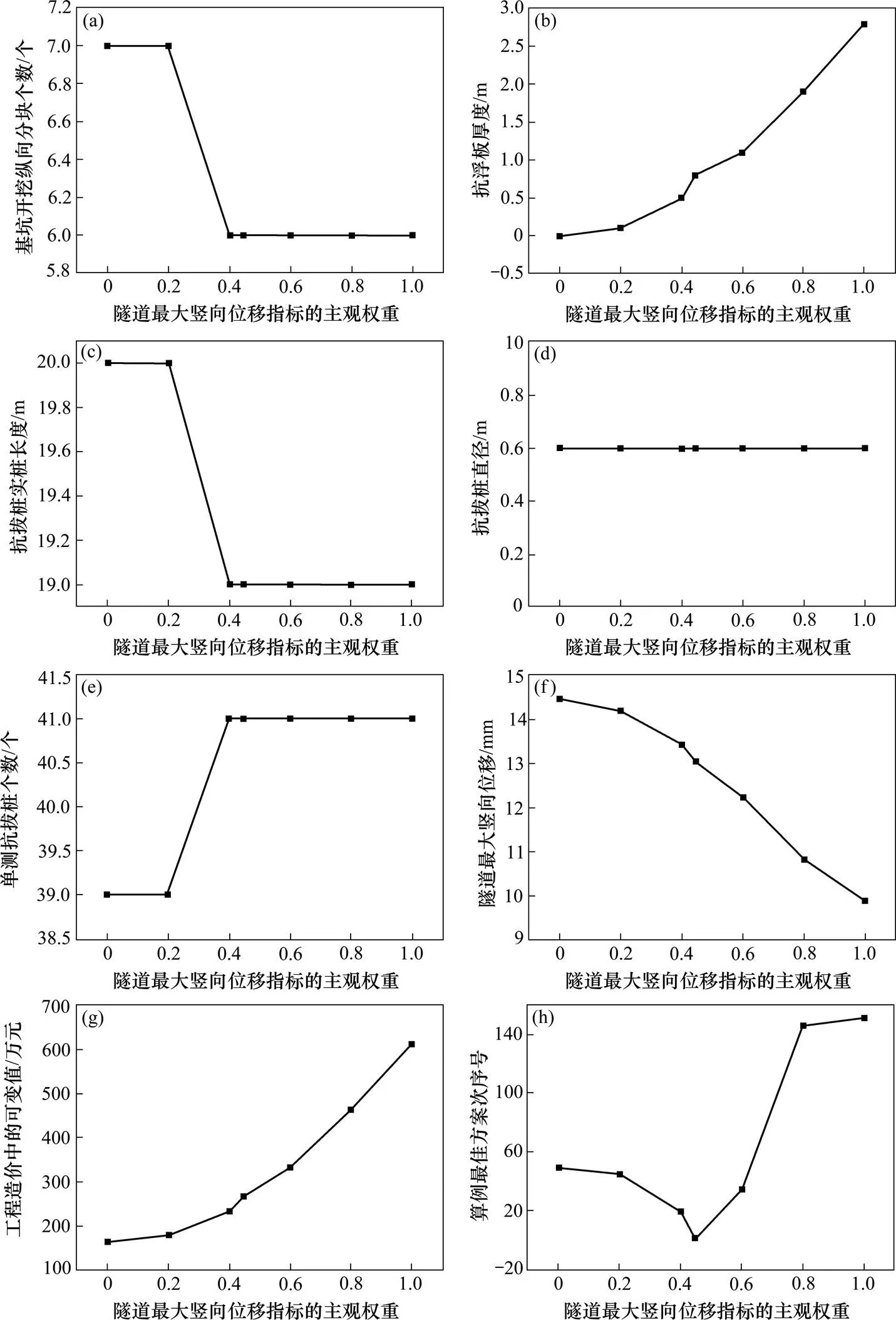
(a) 主观权重对最佳方案中基坑开挖纵向分块个数的影响；(b) 主观权重对最佳方案中抗浮板厚度的影响；(c) 主观权重对最佳方案中抗拔桩实桩长度的影响；(d) 主观权重对最佳方案中抗拔桩直径的影响；(e) 主观权重对最佳方案中单侧抗拔桩个数的影响；(f) 主观权重对最佳方案中隧道最大竖向位移的影响；(g) 主观权重对最佳方案中工程造价中可变值的影响；(h) 主观权重对前文算例最佳方案次序的影响

由图5(a)可知，当隧道最大竖向位移指标的主观权重小于0.4时，最佳方案中基坑开挖纵向分块个数均为7个。当隧道最大竖向位移指标的主观权大于0.4时，最佳方案中基坑开挖纵向分块个数均为6个；由图5(b)可知，随着隧道最大竖向位移指标主观权重增大，最佳方案中抗浮板厚度不断增大，且增大幅度越来越大，表明抗浮板厚度对决策的重要性越来越大；由图5(c)可知，当隧道最大竖向位移指标的主观权重小于0.4时，最佳方案中抗拔桩实桩长度均为20 m。当隧道最大竖向位移指标的主观权大于0.4时，最佳方案中抗拔桩实桩长度均为19 m；由图5(d)可知，无论隧道最大竖向位移指标的主观权重如何变化，最佳方案中抗拔桩直径均为0.6 m，即取值范围内的最小值。因此，只考虑抗拔桩对下覆地铁隧道控制作用和工程造价的情况下，抗拔桩直径应适当减小；由图5(e)可知，当隧道最大竖向位移指标的主观权重小于0.4时，最佳方案中单侧抗拔桩个数均为39个。当隧道最大竖向位移指标的主观权大于0.4时，最佳方案中单侧抗拔桩个数均为41个，即取值范围内的最大值。因此，在考虑群桩效应容许最小桩纵向间距的情况下，单侧抗拔桩个数应适当增加；由图5(h)可知，随着隧道最大竖向位移指标主观权重增大，前文算例最佳方案次序先往前移再往后退。

将图5(a)～5(h)归一化处理，得到不同最佳方案中变量、目标函数值和前文算例最佳方案的次序号对比结果如图6所示。

图6 主观权重对归一化后各因变量的影响

由第3节可知，2个指标主观权重的大小由主观评估决定。因此结合图6可知，主观评估不影响最佳方案中抗拔桩直径，对最佳方案中抗浮板厚度的影响最大。主观评估对各因变量影响大小的排序为：最佳方案中抗浮板厚度>前文算例最佳方案次序号>最佳方案中工程造价可变值>最佳方案中隧道最大竖向位移>最佳方案中基坑开挖纵向分块个数=最佳方案中抗拔桩实桩长度=最佳方案中单侧抗拔桩个数>最佳方案中抗拔桩直径。

5 结论

1) 通过本文科学的双目标优化和决策，得到的最佳方案比初始方案隧道最大竖向位移减少23.3%，工程造价中的可变值减少36.9%，与最优水平的接近指数增加60.9%，证明本文对地铁隧道上方基坑工程的双(或多)目标优化设计方法有效可行；最佳方案的5个设计变量取值依次为：基坑开挖纵向分块个数为6个，抗浮板厚度为0.7 m，抗拔桩实桩长度为19 m，抗拔桩直径为0.6 m，单侧抗拔桩个数41个。最佳方案的2个优化目标取值依次为：隧道最大竖向位移为13.044 mm，工程造价中的可变值为266.347万元。

2) 由主观权重对各因变量的影响分析可知，当隧道最大竖向位移指标的主观权重小于0.4时，最佳方案中基坑开挖纵向分块个数均为7个，抗拔桩实桩长度均为20 m，单侧抗拔桩个数均为39个。当隧道最大竖向位移指标的主观权大于0.4时，最佳方案中基坑开挖纵向分块个数均为6个，抗拔桩实桩长度均为19 m，单侧抗拔桩个数均为41个；随着隧道最大竖向位移指标主观权重增大，抗浮板厚度对决策的重要性越来越大；只考虑抗拔桩对下覆地铁隧道控制作用和工程造价的情况下，抗拔桩直径应适当减小；在考虑群桩效应容许最小桩纵向间距的情况下，单侧抗拔桩个数应适当增加。

3) 由归一化处理主观权重对各因变量的影响分析可知，主观评估对各因变量影响大小的排序为：最佳方案中抗浮板厚度>前文算例最佳方案次序号>最佳方案中工程造价可变值>最佳方案中隧道最大竖向位移>最佳方案中基坑开挖纵向分块个数=最佳方案中抗拔桩实桩长度=最佳方案中单侧抗拔桩个数>最佳方案中抗拔桩直径。

[1] 曹顺, 钱德玲, 魏雪云, 等. 隧道基坑开挖卸载对既有地铁的影响与变形控制[J]. 合肥工业大学学报(自然科学版), 2014, 37(12): 1479−1482, 1536. CAO Shun, QIAN Deling, WEI Xueyun, et al. Influence of deep foundation pit excavation on underlying metro tunnel and control measure[J]. Journal of Hefei University of Technology, 2014, 37(12): 1479−1482, 1536.

[2] 魏纲. 基坑开挖对下方既有盾构隧道影响的实测与分析[J]. 岩土力学, 2013, 34(5): 1421−1428. WEI Gang. Measurement and analysis of impact of foundation pit excavation on below existed shield tunnels[J]. Rock and Soil Mechanics, 2013, 34(5): 1421− 1428.

[3] 姚爱军, 张剑涛, 郭海峰, 等. 地铁盾构隧道上方基坑开挖卸荷——加载影响研究[J]. 岩土力学, 2018, 39(7): 2318−2326, 2335. YAO Aijun, ZHANG Jiantao, GUO Haifeng, et al. Influence of unloading-loading of foundation on shield tunnel underneath[J]. Rock and Soil Mechanics, 2018, 39(7): 2318−2326, 2335.

[4] 左自波, 黄玉林, 吴小建, 等. 基坑施工对下方双线地铁隧道影响的数值模拟[J]. 北京交通大学学报, 2019, 43(3): 50−56. ZUO Zibo, HUANG Yulin, WU Xiaojian, et al. Numerical simulation of influence of excavation on underneath double metro tunnel[J]. Journal of Beijing Jiaotong University, 2019, 43(3): 50−56.

[5] 林杭, 陈靖宇, 郭春, 等. 基坑开挖对邻近既有隧道变形影响范围的数值分析[J]. 中南大学学报(自然科学版), 2015, 46(11): 4240−4247. LIN Hang, CHEN Jingyu, GUO Chun, et al. Numerical analysis on influence of foundation pit excavation on deformation of adjacent existing tunnel[J]. Journal of Central South University (Science and Technology), 2015, 46(11): 4240−4247.

[6] 曹前. 既有地铁隧道上方基坑开挖特性研究[J]. 铁道标准设计, 2018, 62(5): 109−115. CAO Qian. Research on characteristics of foundation pit excavation above existing subway tunnel[J]. Railway Standard Design, 2018, 62(5): 109−115.

[7] 胡志敏. 小竖井工法在地铁隧道上方基坑开挖中的应用研究[D]. 广州: 广州大学, 2018. HU Zhimin. Application of small shaft construction method in foundation pit excavation above metro tunnel[D]. Guangzhou: Guangzhou University, 2018.

[8] 深圳市城市轨道交通安全保护区施工管理办法(暂行)[S]. Measures for construction management of safety protection zone of urban rail transit (interim) in Shenzhen[S].

[9] Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: Solving problems with box constraints[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577−601.

[10] TANG Huichin, YANG Shentai. Optimizing three- dimensional constrained ordered weighted averaging aggregation problem with bounded variables[J]. Mathematics, 2018, 6(9): 172−176.

[11] JIN Feifei, NI Zhiwei, CHEN Huayou, et al. Multiple attribute group decision making based on interval-valued hesitant fuzzy information measures[J]. Computers and Industrial Engineering, 2016, 101: 103−115.

[12] LAI Chengguang, CHEN Xiaohong, CHEN Xiaoyu, et al. A fuzzy comprehensive evaluation model for flood risk based on the combination weight of game theory[J]. Natural Hazards, 2015, 77(2): 1243−1259.

[13] 王会东, 何世繁, 潘晓宏, 等. 基于博弈论权重集化模型的多属性群决策VIKOR方法[J]. 统计与决策, 2019, 35(15): 39−43. WANG Huidong, HE Shifan, PAN Xiaohong, et al. A new VIKOR method for multi-attribute group decision- making based on game theory weight integration model [J]. Statistics and Decision, 2019, 35(15): 39−43.

[14] HU Yanjuan, WU Lizhe, SHI Chao, et al. Research on optimal decision-making of cloud manufacturing service provider based on grey correlation analysis and TOPSIS[J]. International Journal of Production Research, 2020, 58(3): 748−757.

[15] Kannan V S, Lenin K, Navneethakrishnan P. Machining parameters optimization in laser beam machining for micro elliptical profiles using TOPSIS method[J]. Materials Today: Proceedings, 2020, 21(Pt 1): 727−730.

Optimization design for foundation pit above metro tunnel based on NSGA2 genetic algorithm

BU Kangzheng1, ZHAO Yong2, ZHENG Xianchang3

(1. Shenzhen Water Planning and Design Institute Co., Ltd., Shenzhen 518000, China;2. Sino-Railway South Constructing Group Co., Ltd., Shenzhen 518052, China;3. School of Civil Engineering, Guangzhou University, Guangzhou 510006, China)

To effectively control the vertical displacement of the metro tunnel under the foundation pit and reduce the construction cost of the foundation pit as much as possible, based on NSGA2 genetic algorithm, the Pareto optimal solution set was obtained by taking 5 key design parameters of the foundation pit controlling the vertical displacement of the underlying metro tunnel as the optimal design variables, the maximum vertical displacement of the tunnel and the variable value of construction cost as the optimization objectives. Combining the expert scoring-COWA operator-game theory combination weighting method and TOPSIS method, the optimal scheme was selected from Pareto optimal solution set, and the effect on the change of the subjective weight of expert scoring on the design variables, objective function values and some other parameters of the best scheme were analyzed. The results show that the maximum vertical displacement of the tunnel in the best scheme is 23.3% less than that in the initial scheme, and the variable value of construction cost is 36.9% less than that in the initial scheme.It proves the effectiveness of the optimization design method for the foundation pit above the metro tunnel.

foundation pit; metro tunnel; vertical displacement; construction cost; optimization design;NSGA2 genetic algorithm

U451

A

1672 − 7029(2021)02 − 0459 − 09

10.19713/j.cnki.43−1423/u.T20200287

2020−04−09

中国中铁股份有限公司科技开发计划重点课题(2016-重点-17)

郑先昌(1969−)，男，湖北黄陂人，教授，博士，从事地下工程理论与应用等方面的研究；E−mail：zhengxianchang@gzhu.edu.cn

(编辑 阳丽霞)