基于混合PSO-RBF神经网络的铁路隧道岩爆分级预测

高磊，刘振奎，张昊宇

基于混合PSO-RBF神经网络的铁路隧道岩爆分级预测

高磊，刘振奎，张昊宇

(兰州交通大学 土木工程学院，甘肃 兰州 730070)

岩爆是铁路隧道建设中主要灾害之一。为了准确预测铁路隧道岩爆烈度等级，以岩石应力系数σ/、岩石脆性系数/以及弹性能量指数W作为岩爆烈度评价指标，提出一种基于混合粒子群优化算法优化的径向基(RBF)神经网络岩爆预测模型。首先在国内外研究成果基础上，选取80组已有岩爆实例作为模型基础数据；然后运用结合了模拟退火算法的粒子群算法(混合PSO)改进径向基神经网络，通过训练数据选取最优的权值和基函数标准差，得到混合PSO-RBF神经网络岩爆烈度预测模型；最后将模型应用于实际铁路隧道工程进行验证。研究结果表明：该模型兼顾个体最优和全局最优，能够正确、有效的对铁路隧道岩爆等级做出预测，为铁路隧道岩爆预测提供了一种新方法。

铁路隧道；模拟退火算法；粒子群算法；RBF神经网络；交叉验证；岩爆烈度分级预测

岩爆是指处于高应力或极限平衡状态的硬、脆性围岩的弹性应变能超过岩体的储能极限时，多余的能量快速释放，在临空岩体中发生突发式破坏的现象。岩爆是隧道施工中常见地质灾害，表现为岩石下落或弹出，并伴有声响，严重时爆落规模大，直接威胁到施工设备和人员的安全。例如，2011年8月7日，雅西路泥巴山隧道出口段发生大型重度岩爆，将拱架、锚杆支护系统破坏；2014年3月9日，云南贡山独龙江隧道内发生岩爆，造成岩石塌落事故，3名施工人员遇难。随着我国铁路建设的飞速发展，隧道工程的占比也逐渐提高，为保证隧道工程施工质量、工期、投资和人员设备安全，提前预测岩爆等未知灾害的发生，采取相应的举措，对于高地应力铁路隧道设计和施工都具有重要意义[1]。国内外学者通过研究岩爆发生机理及影响因素，从多个角度提出了岩爆风险等级的判别依据，为岩爆预测理论打下了坚实的基础，如Russense判据、Turchaninov判据及陆家佑判据等。近年来，关于岩爆预测的研究工作迅速发展，各种各样的基于多因素分析理论和实际案例分析的岩爆预测方法被相继提出。DONG等[2]将不同指标进行组合划分，运用随机森林进行有监督学习，建立随机森林预测模型，在地下工程岩爆等级分类中取得了良好的效果；李任豪等[3]用粒子群优化算法寻优取得RBF神经网络的内部参数，建立PSO-RBF神经网络预测模型，显著提高RBF神经网络的预测精度，为岩爆预测提供新的方法；刘海涛等[4]通过将蒙特卡洛方法与数值实验相结合，提出了深埋隧洞岩爆的抽样概率预测的方法，为深埋隧洞岩爆预测提供有益的参考；周鑫隆等[5]提出基于多因素灰靶决策理论的岩爆烈度评价方法，解决小样本情形下岩爆烈度等级评价的模糊性和不确定性问题，从而给出更为确切的岩爆烈度判定结果；黄建等[6]用熵权法和CRITIC确定指标的组合权重，依据国内外48组岩爆实例数据，建立基于不确定性人工智能理论的多维正态云模型；孙臣生[7]通过分析国内外具有代表性的工程实例，运用改进的BP神经网络，实现了岩爆预测中非线性理论和网络分析法之间的有机结合。但是岩爆因素分析是一个复杂的非线性问题，大多数研究方法在指标权重的确定过程中的不可避免的具有主观性和随意性，且有些因素用方法理论无法准确描述。在机器学习领域，目前部分基于机器学习的岩爆预测研究中实际案例过少，建立的模型有过拟合现象，泛化性较差。再者，普通PSO-RBF神经网络虽然优于传统RBF神网络，但在训练过程中会出现偶发性陷入局部最优状况，而且寻优过程耗时过长[3]。基于此，本文遴选了最具代表性的3个指标作为评价因子，结合模拟退火算法、粒子群算法和RBF神经网络提出一种混合PSO-RBF神经网络岩爆预测模型，通过训练80组实际样本数据，挖掘出各因素与岩爆烈度等级之间的关系，并运用20折交叉验证对模型准确率进行评估。该模型相比于传统的神经网络，能够显著提高准确率和收敛效率，评价结果更加可靠。

1 指标和数据

1.1 评价指标选取

本文根据徐林生等[8]对岩爆的研究成果，将岩爆烈度分为无岩爆(I级)、轻微岩爆(II级)、中等岩爆(III级)和强烈岩爆(IV级)，每一烈度等级对应的特征判据如表1所示。

表1 岩爆烈度等级划分依据

岩爆发生机制十分复杂，受多种因素共同影响，指标选取需要从多方面考虑。

1) 大多数神经网络模型需要大量数据来驱动，因此选取的岩爆指标应该是常见的，容易测得的且在现有文献中有记载的。

2) 过多的指标不仅会增加预测过程的复杂性，而且会增加模型的训练时长，甚至会影响预测模型的精度。指标过少则导致信息缺少，不能全面反映岩爆发生的条件。因此选取指标要有代表性，能够以最少的指标反映影响岩爆烈度的内因和外因。内因是指岩体自身的脆性、岩石的抗压强度和储存弹性能等因素；外因是指岩体工程的整体地质环境以及环境的变化。

3) 根据影响岩爆发生与否及其烈度大小的主要因素，有3类不同的判别准则：岩爆与洞室围岩应力的关系、岩爆与岩石岩性的关系和岩爆与能量的关系[9]。其中岩石应力系数σ/σ是指围岩最大切向应力和岩石单轴抗压强度的比值，综合反映了围岩应力这一因素对岩爆影响，比值越大，岩爆越剧烈；岩石脆性系数σ/σ通常用岩石单轴抗压强度和岩石单轴抗拉强度比值表示，反映了岩爆发生与否以及剧烈程度跟岩性之间的密切关系，数值越小越容易发生岩爆。弹性能量指数(弹性变形能指数)W反映岩石的能量特征，是岩块在单轴压缩加卸载条件下所释放的弹性应变能和损耗的弹性应变能的比值，其值越大，破坏时释放的能量越多。在实际案例中，岩爆断面形式主要是张拉破坏，并伴有剪切破坏，但在现有文献中的岩爆实例里，抗剪强度记载极少，很难对抗剪强度进行分析，所以认为抗拉强度代表了岩石的抗拉和抗剪2种力学性质[10]。

综上所述，本文综合考虑岩爆与围岩应力、岩性以及岩石能量之间的关系，选取岩石应力系数σ/σ，岩石脆性系数σ/σ以及弹性能量指数W3个参数作为岩爆预测指标。

1.2 数据来源

岩石应力系数σ/σ，岩石脆性系数σ/σ和弹性能量指数W是隧道和矿山中共同存在的共性因素。因此，本文从国内外隧道及矿山井下岩爆倾向研究成果中[4, 8−13]搜集所需的样本数据。获得的数据经过筛选，剔除重复样本和一部分矿井数据，最终保留秦岭隧道，苍岭隧道、锦屏隧洞等80个岩爆实例数据作为岩爆烈度等级预测的研究样本(其中隧道样本占65%，矿井数据占35%)，样本中各等级样本数占比如图1所示，部分数据如表3所示。

图1 各等级样本数据分布

表2 部分岩爆实例样本数据

2 研究方法

2.1 RBF神经网络

径向基函数(Radial Basis Function，RBF)是一种结构简单，收敛速度快，能够逼近任意非线性函数的网络。1988年Broomhead和Lowe根据生物神经元具有局部响应原理，将径向基引入神经网络中，很快RBF神经网络被证明对非线性网络具有一致逼近的性能。RBF神经网络是一种由输入层、隐含层和输出层构成的前馈神经网络，其基本思想为：用RBF作为隐单元的“基”构成隐含层空间，就可以直接将输入矢量映射到隐空间。本文RBF神经网络结构如图2所示。

图2 径向基函数网络结构

RBF函数有多种选取中心的学习规则。本文中使用自组织选取中心法[14]，学习算法具体步骤(基于K-Maens聚类方法求解基函数中心)如下：

1) 网络初始化

2) 将训练样本按最邻近规则分类

按照x与中心c之间的欧氏距离，将x分配到各个聚类集合C(=1,2,…,)中。

3) 重新调整聚类中心

计算个聚类集合中样本的平均值,代替c作为新的聚类中心，重复步骤2)，直到聚类中心不发生变化，所得的即为RBF神经网络的基函数中心。

4) 计算隐含层第个节点的输出值。

RBF神经网络中常用的RBF函数为高斯函数，输出值可由激活函数(1)得到：

5) 计算输出值。

RBF神经网络的输出为

式中：w为隐含层到输出层的连接权值；y为第个样本对应模型的输出。

2.2 基于模拟退火的PSO算法原理

粒子群优化算法(Particle Swarm Optimization)是受鸟群觅食行为的启发而衍生的算法，简称粒子群算法。粒子群算法适用于动态多目标环境中寻优，能够更快的、以较大的概率收敛于最优解，能够兼顾个体性和全局性。其缺点是：由于函数寻优过程中主要依赖粒子之间的个体信息和全局信息来不断更新粒子的位置和速度，使粒子逐步靠近最优解，所以PSO算法易早熟，且后期收敛速度较慢。

模拟退火(simulated annealing)算法是通过模拟高温物体退火过程找到优化问题的全局最优解的一种智能算法。其基本思想是：首先产生一个初始解作为当前解，然后在当前解的领域中，以概率选择一个非局部最优解，并令这个解再重复下去，从而保证不会陷入局部最优。模拟退火是一种搜索过程引入了随机因素的Greedy算法，它以一定的概率来接受一个比当前解要差的解，因此有可能会跳出局部的最优解陷阱，收敛于全局最优解区域，拥有较高的搜索精度。

本文将模拟退火算法与粒子群算法相结合，形成一种混合粒子群优化(SA-PSO)算法[15]．该混合算法以基本粒子群算法运算流程作为主导，在粒子更新速度和位置过程中，加入模拟退火机制，实现取长补短。相比单一算法，混合粒子群算法不容易出现早熟收敛的情况，而且收敛速度也有了明显的提升，从而提升了算法的整体性能。具体步骤为：

1) 随机设置各粒子速度和位置。

假设D维空间有个个体，第个个体的位置和速度定义如下：

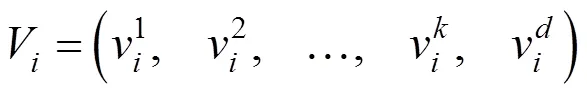
2) 保存个体极值和全局极值。

评价每个粒子的适应值，将粒子的位置和适应值保存为粒子的个体极值Best，将所有个体极值中的最优极值保存为全局极值Best。

3) 确定初始温度。

初始温度和退温方法采用如下的算法

其中：T为第1次迭代的初始温度；为退火常数惯性权重；为总迭代次数。

4) 确定当前温度下各粒子的适应值。

5) 更新位置和速度

6) 比较当前Best和Best，更新Best，然后用式(4)进行退温操作。

7) 当达到停止条件时，输出结果；否则返回第(4)步继续搜索。

2.3 基于混合PSO-RBF的岩爆预测模型

本文所提出的岩爆等级预测模型是基于MATLAB2018b环境下建立的，首先用K-Means聚类方法求得RBF神经网络的中心，然后将模拟退火算法应用于粒子群算法中，对RBF神经网络内部参数进行优化，最终训练出混合PSO-RBF神经网络岩爆等级预测模型。研究流程如图3所示，具体建模步骤如下。

1) 样本分割

按照机器学习常用划分方法，将样本按4:1的比例分为测试集和训练集。训练集用于模型训练和更新参数；测试集用于检验模型的准确率，调整参数(聚类中心个数，迭代次数、学习率等)，监控模型是否发生过拟合，并在模型最终训练完成后，评估其泛化能力，测试其真正的预测准确率。

2) 模型输入输出

输入样本数据用mapminmax命令进行归一化处理，归一化后样本区间为[0,1]，使得数据无量纲化，加快收敛速度。模型训练样本输出用“1”，“2”，“3”，“4”表示岩爆的4个等级(无岩爆I级、轻微岩爆II级、中级岩爆III级和强烈岩爆IV级)。测试样本输出结果用round函数取整。

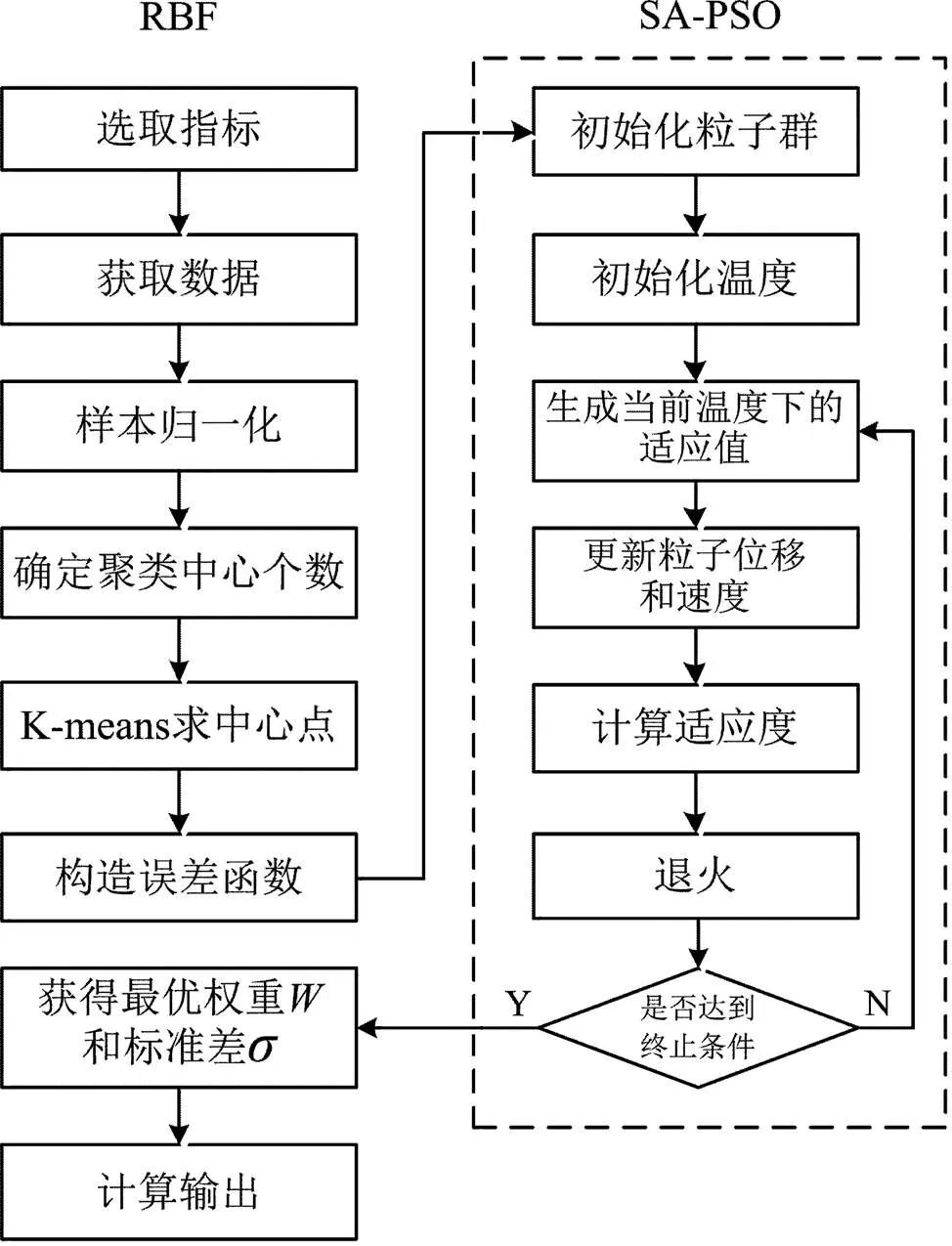
图3 混合PSO-RBF神经网络预测模型流程图

3) 隐含层节点确定

从理论上来说，隐含层节点数增多，可以使径向基神经网络达到任意精度。但在实际应用中，隐含层节点数太多，会导致算法训练时间增长，学习成本增加，而且会降低模型的泛化能力和容错能力，出现过度拟合现象。本文中RBF神经网络的隐含层为一层，神经元节点数用基于K-Means聚类的RBF神经网络进行试算，聚类中心为20时，可达到很好的逼近效果。因此，选取隐含层节点个数为20，RBF的中心(c)为K-Means聚类取得的20个聚类中心。

4) 构造适应度函数

神经网络的性能通常以均方误差MSE(mean- square error)来衡量。本文则选用神经网络均方误差MSE的计算公式作为粒子群算法寻优的适应度计算函数。用混合粒子群算法求最小均方误差下的权重和基函数标准差，既为此模型的最优参数。

5) 计算最优权值

设置SA-PSO算法的基础参数:学习因子1,2均为0.5，初始种群数目=200，最大迭代次数=60，降温速率=0.85。

6) 模型输出

混合PSO-RBF神经网络的输出可以用式(1)和(2)得到。

7) 交叉验证

本文按照交叉验证方法进行模型训练和准确率评估。

将训练集和测试集带入模型进行20次训练和测试，每次都按照4:1比例随机划分训练集和测试集；将每次模型训练后得到的适应度函数最小值、全局最优权重和方差、测试集样本准确分类率、以及测试集样本均方误差都做记录；训练完成后，将20次测试集样本准确分类率和均方误差的平均值作为本文模型的实际准确率和均方误差；最后选取准确率和均方误差最接近平均值的模型作为隧道岩爆倾向度预测模型。此方法可以有效避免过拟合现象，得到最佳预测模型。由交叉验证得到样本训练集平均均方误差(适应度函数平均最小值)为0.057，测试集平均均方误差为0.135，准确率为96.25%，根据平均值选取最佳模型的和。

8) 模型对比

普通RBF神经网络的径向基函数扩展速度、神经元最大数目等参数需要依靠经验设置，受人为因素影响大，容易出现过度拟合现象，导致测试集分类错误率较高，不能对岩爆烈度等级做出准确 预测。

普通PSO-RBF模型测试结果不稳定，训练集的均方误差在0.08～0.11之间，测试集均方误差在0.2～0.4之间，准确率在87.5%～93.75%之间，且迭代次数均在60次以上。

本文提出的混合PSO-RBF模型参数设置少，每次训练过程中，迭代次数达35次之后收敛到最小值，训练集均方误差在0.05～0.07之间，16个测试集样本的均方误差均小于0.3。20次训练后适应度函数的平均最小值为0.057，测试集平均准确率为96.25%以上。通过对比可以看出，混合PSO-RBF模型训练过程会很大程度上避免陷入局部最优情况，收敛更快，耗时更短，准确率也明显提高。3种模型详细对比如表3所示，优化过程均方误差曲线如图4所示。

图4 均方误差变化曲线

表3 模型对比

3 工程应用

3.1 工程概况及应用

改建铁路成昆线重点工程——老鼻山隧道位于四川省南部，属于我国一、二阶地间过渡地带，处峨边县毛坪镇范店子到峨边南站区间，为双线隧道，全长13 579 m。隧道进口紧邻鱼洞河大桥，出口与峨边车站相接，隧道属大渡河峡谷构造剥蚀地貌，地面高程625～1 350 m，最大埋深约710 m。隧址区为单斜构造，岩层层理为N20°E/20°NW，陡倾节理发育，主要为N40°W/65°NE，N50°E/90°，区内发育苦竹坝逆断层。苦竹坝逆断层与线路相交于D1K202+266，断层走向N75°～85°E，北东倾向，倾角50°，断距不详。断层上盘为玄武岩地层，下盘为砂岩、泥岩、页岩地层。该隧道施工以新奥法施工为主，全隧共设3座横洞，1号横洞全长815 m，最大埋深523 m，2号横洞全长1 867 m，最大埋深703 m，3号横洞全长1 785 m，最大埋深611 m。

由于老鼻山隧沿线玄武岩、灰岩等硬岩，岩体完整性好，抗压强度较高，且具有较好的弹性和脆性，因此该隧道在施工时极易发生岩爆。本文以老鼻山隧道横洞施工中发生的3处岩爆段实验数据作为实例分析样本，其中2处发生在灰岩中，另外一处发生在玄武岩中。D1K205+720处，隧道埋深520 m，最大主应力23.8 MPa，最大切向应力34.36 MPa，该处灰岩自由浸水饱和抗压强度平均值为58～70 MPa。该处岩石构造节理较为发育，岩体新鲜且坚硬，隧道施工中，受构造节理控制和地应力的影响，板状灰岩时有出现剥离掉块及弹射、飞出现象。D1K205+330处，隧道埋深437 m，最大主应力15.27 MPa，最大切向应力24.50 MPa，该处灰岩单轴抗压强度70.30 MPa，实际施工中，岩块发生小规模剥裂剥落现象。D1K208+450附近，深度650～700 m，最大主应力50.1～51.09 MPa，最大切向应力63.83～85.36 MPa。该处岩石玄武岩、灰岩节理较发育，岩体干燥，实际施工中发生岩石爆裂声响，石块弹射、岩体坍塌现象。详细数据如表4所示。

3.2 结果与讨论

取改建铁路成昆线老鼻山隧道发生岩爆的5个样本点，分别用混合PSO-RBF模型、PSO-RBF模型和普通RBF模型进行预测，得到预测结果如表5所示。

表4 待预测隧道段实际等级和指标数据

表5 老鼻山隧道岩爆数据和预测结果

1) 混合POS-RBF神经网络模型正确预测了五个样本，PSO-RBF模型和普通RBF预测的样本均出现错误。

2) 对比3种模型的输出结果(图5)，混合PSO- RBF神经网络预测模型的实际输出结果与期望输出结果(实际等级)之间的误差最小。

图5 模型输出对照

可以看出，通过模拟退火算法和粒子群优化算法相结合的混合算法优化的RBF神经网络，具有强大的抗噪和修复能力，能够较大程度的消除训练集中异常数据和错误数据的干扰，准确的进行岩爆烈度等级预测。

4 结论

1) 通过参考相关文献，选取岩石应力系数σ/，岩石脆性系数/以及弹性指数W作为岩爆烈度评价指标，使建立的模型能充分体现岩爆发生与围岩应力的关系、岩爆发生于岩性的关系以及岩爆发生于能量的关系。

2) 通过机器学习分析80组实际案例数据，避开权重调节问题，减少人为因素的主观影响。通过混合粒子群算优化径向基神经网络，不仅比普通PSO-RBF模型运算速度加快，而且能避开噪声数据的影响，精确度达到96.25%。最后通过老鼻山隧道实际应用，证明了本文模型对铁路隧道岩爆烈度等级预测的适用性和准确性。

3) 随着铁路建设的快速发展，铁路隧道岩爆数据将越来越多，人工智能在数据处理方面的优势已逐步显露，通过机器学习方法处理数据，更能客观、准确的反映各项因素对岩爆烈度的影响。

[1] 朱自强, 郭有军, 刘涛影. 地质雷达超前地质预报正演模拟及应用研究[J]. 铁道科学与工程学报, 2018, 15(1): 148−155. ZHU Ziqiang, GUO Youjun, LIU Taoying. Advance geological forecast forward modeling of geological radar and its application[J]. Journal of Railway Science and Engineering, 2018, 15(1): 148−155.

[2] DONG Longjun, LI Xibing, PENG Kang. Prediction of rockburst classification using Random Forest[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(2): 472−477.

[3] 李任豪, 顾合龙, 李夕兵, 等. 基于PSO-RBF神经网络模型的岩爆倾向性预测[J]. 黄金科学技术, 2020, 28(1): 134−141. LI Renhao, GU Helong, LI Xibing, et al. A PSO-RBF neural network model for rockburst tendency prediction [J]. Gold Science and Technology, 2020, 28(1): 134−141.

[4] 刘海涛, 周辉, 卢景景, 等. 深埋隧洞岩爆的抽样概率预测方法[J]. 现代隧道技术, 2018, 55(6): 59−66. LIU Haitao, ZHOU Hui, LU Jingjing, et al. A sampling- based probabilistic prediction method of rockbursts in deep-buried tunnels[J]. Modern Tunnelling Technology, 2018, 55(6): 59−66.

[5] 周鑫隆, 章光, 李俊哲, 等. 灰靶决策理论在岩爆烈度等级评价中的应用[J]. 中国安全科学学报, 2019, 29(5): 19−24. ZHOU Xinlong, ZHANG Guang, LI Junzhe, et al. Application of grey target decision-making theory in evaluation of rock burst intensity[J]. China Safety Science Journal, 2019, 29(5): 19−24.

[6] 黄建, 夏元友, 吝曼卿. 基于改进组合赋权的岩爆多维云模型预测研究[J]. 中国安全科学学报, 2019, 29(7): 26−32. HUANG Jian, XIA Yuanyou, LIN Manqing. Study on prediction of rock burst by multi-dimensional cloud model based on improved combined weight[J]. China Safety Science Journal, 2019, 29(7): 26−32.

[7] 孙臣生. 基于改进MATLAB-BP神经网络算法的隧道岩爆预测模型[J]. 重庆交通大学学报(自然科学版), 2019, 38(10): 41−49. SUN Chensheng. A prediction model of rock burst in tunnel based on the improved MATLAB-BP neural network[J]. Journal of Chongqing Jiaotong University (Natural Science), 2019, 38(10): 41−49.

[8] 徐林生, 王兰生, 李永林. 岩爆形成机制与判据研究[J]. 岩土力学, 2002, 23(3): 300−303. XU Linsheng, WANG Lansheng, LI Yonglin. Study on mechanism and judgement of rockbursts[J]. Rock and Soil Mechanics, 2002, 23(3): 300−303.

[9] 王元汉, 李卧东, 李启光, 等. 岩爆预测的模糊数学综合评判方法[J]. 岩石力学与工程学报, 1998, 17(5): 493−501. WANG Yuanhan, LI Wodong, LI Qiguang, et al. Method of fuzzy comprehensive evaluations for rockburst prediction[J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(5): 493−501.

[10] 贾义鹏. 岩爆预测方法与理论模型研究[D]. 杭州: 浙江大学, 2014: 47−47. JIA Yipeng. Study on prediction method and theorial model of rockburst[D]. Hangzhou: Zhejiang University, 2014: 47−47.

[11] LI Tianzheng, LI Yongxin, YANG Xiaoli. Rock burst prediction based on genetic algorithms and extreme learning machine[J]. Journal of Central South University, 2017, 24(9): 2105−2113.

[12] 汪华斌, 卢自立, 邱杰汉, 等. 基于粒子群算法优化支持向量机的岩爆预测研究[J]. 地下空间与工程学报, 2017, 13(2): 364−369. WANG Huabin, LU Zili, QIU Jiehan, et al. Prediction of rock burst by improved particle swam optimization based support vector machine[J]. Chinese Journal of Underground Space and Engineering, 2017, 13(2): 364− 369.

[13] ZHOU Jian, LI Xibing, SHI Xiuzhi. Long-term prediction model of rockburst in underground openings using heuristic algorithms and support vector machines[J]. Safety Science, 2012, 50(4): 629−644.

[14] 吴华稳, 甄津, 王宇, 等. 基于径向基神经网络的铁路客货运量预测研究[J]. 铁道科学与工程学报, 2014, 11(4): 109−114. WU Huawen, ZHEN Jin, WANG Yu, et al. Railway passenger and freight prediction based on RBF neural network theory[J]. Journal of Railway Science and Engineering, 2014, 11(4): 109−114.

[15] Nayeri S, Asadi-Gangraj E, Emami S. Metaheuristic algorithms to allocate and schedule of the rescue units in the natural disaster with fatigue effect[J]. Neural Computing and Applications, 2019, 31(11): 7517−7537.

Prediction of rockburst classification of railway tunnel based on hybrid PSO-RBF neural network

GAO Lei, LIU Zhenkui, ZHANG Haoyu

(School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

Rock burst is one of the main disasters in railway tunnel construction. In order to accurately predict the rockburst intensity grade of railway tunnel, a rockburst prediction model based on radial basis (RBF) neural network optimized by hybrid particle swarm optimization algorithm was proposed in this paper, which stress coefficient (σ/σ), brittleness coefficient (σ/σ) and elastic energy index of rock (W) were chosen as the rockburst prediction indexes. Firstly, based on the research results at home and abroad, 80 groups of existing rock burst cases were selected as the basic data of the model. Then, the particle swarm optimization algorithm combined with simulated annealing algorithm (Hybrid PSO) was used to improve the radial basis function neural network, and the optimal weight () and the basis function standard deviation () were selected by training the data, and the prediction model of rock burst intensity based on hybrid PSO-RBF neural network was obtained. Finally, the model was applied to the actual railway tunnel engineering for verification. The case study shows that the model takes into account both individual optimization and global optimization, can correctly and effectively predict the rockburst level of railway tunnels, and provides a method and approach for rockburst prediction of railway tunnels.

railway tunnel; simulated annealing; particle swarm optimization; RBF neural network; cross- validation; prediction of intensity classification of rockburst

TU45

A

1672 − 7029(2021)02 − 0450 − 09

10.19713/j.cnki.43−1423/u.T20200352

2020−04−26

国家自然科学基金资助项目(11662007，51268031)

刘振奎(1969−)，男，河北平泉人，教授，从事工程管理、工程财务方面的研究；E−mail：liuzk@mail.lzjtu.cn

(编辑 涂鹏)