应用六西格玛统计技术对A型肉毒毒素中间品量器的分析

魏子昊，陆俭，苗承辉，张雪平，张锡云

（兰州生物技术开发有限公司，甘肃 兰州 730046）

量器（measuring container）是指具有一定容积并可作为计量器具的容器。根据量器工作用途的不同，可分为量入式量器和量出式量器。量入式量器是测量注入量器（内壁干燥）内液体体积的量器。量出式量器则是用于测量从量器内部排出液体体积的量器［1］。在生物、化学、医学领域中常被用到的分度吸量管（以下简称吸管）、滴定管、移液器等就属于量出式量器［2］。

注射用A 型肉毒毒素（衡力®）是我国自主开发的第一个用于临床的微生物毒素。至今已上市20 余年，用于治疗眼睑痉挛，面肌痉挛，斜视等肌张力障碍性疾病和暂时性改善中重度眉间纹等医学美容领域［3］。注射用A 型肉毒毒素（衡力®）每瓶（100 u） 活性药用成分（API） 含量仅为5 ng,1 ng=10-9g，含量极其微量，100 u 制品中每ng 毒素的活性单位含量（u/ng）高达21～24［4］。基于每毫升API 用量的准确性、价值高的特性，其管理者必须在每个环节中对肉毒毒素中间品的取用进行严格、精细的控制。

本文针对A 型肉毒毒素中间品取用时所用的量器（移液器、分度吸量管）应用六西格玛（6σ）管理方法结合统计学工具，通过对测量得出的结果进行分析，确定了最佳量器组合及其影响因素［5-7］，对指导实际操作和制定相关的控制措施提供理论依据，对制品的质量提升提供支持数据。

1 材料与方法

1.1 材料与仪器

注射用水为兰州生物技术开发有限公司制备；无菌中管；分度吸量管；移液器枪头。XP603S 电子天平梅特勒托利多公司（经甘肃省计量院计量）；移液器（经第三方计量）。

1.2 实验方法

1.2.1 量器实际量取体积检测方法 用量器吸取额定体积的容纳介质（注射用水）至一次性中管，随后在分析天平中称重，所得重量（注射用水+空管）减去空管重量（预先称重）即为量器的量取重量。将注射用水密度近似认为1 g/mL，则量器量取注射用水的重量即为体积。

1.2.2 数据统计 利用Minitab 软件将测量值（量取体积）进行统计计算，根据结果得出分析结论。

1.2.3 量器线性与偏倚分析 实验使用2 种品牌最大量程为10 mL 的移液器交换搭配2 种品牌的枪头、使用最大量程为10 mL 的吸管搭配三通吸球（以下简称吸球），依次量取2、6、10 mL 注射用水并测量实际量取体积，研究2 种10 mL 量器的线性与偏倚情况，实验分为a、b、c、d、e 共5组。见表1。

表1 量器线性与偏倚分析实验设计

1.2.4 吸管变异源分析 根据2 种量器的线性与偏倚分析结果，选择无偏倚的吸管作为优化对象。对其进行单因素分析，双因素交叉、嵌套设计进行实验，分析得到影响吸管量取效果的变异源。

①吸管单因素分析。选择两名不同人员使用吸管+吸球量取10 mL 注射用水，以研究不同人员使用吸管时的差异。

②吸管双因素交叉设计分析。选取吸球、吸管为两个主要因素。选取同品牌1#吸球、2#吸球两个水平，以量取10 mL 注射用水为指标，进行交叉设计（见表2），测试同品牌同型号吸管间的差异。

③吸管双因素嵌套设计分析。选取实验人员、实验次数为两个主要因素。选取实验人员1、2、3三个水平，选取实验次数1、2、3 三个水平，以量取10 mL 注射用水为指标，进行双因素嵌套设计（见表3），对其进行变异源分析。

表2 双因素交叉设计因素与水平

表3 双因素嵌套设计因素与水平

2 结果

2.1 量器线性与偏倚分析

a 组实验的整体偏倚为-0.0577333，故可判断其在2 mL、6 mL、10 mL 处均有偏倚，且参考值为6 mL 时偏倚严重存在；因线性回归的斜率差异无统计学意义（P=0.268），故线性方程不成立，偏倚不可修正。

b 组实验的整体偏倚为-0.0647333，整体偏移百分率为0.5，差异有统计学意义（P=0.000），所以判定整体存在偏倚，且在6 mL 处偏倚严重；线性回归的斜率差异无统计学意义（P=0.245），线性方程不成立，故偏倚不可修正。

c 组实验整体存在偏倚，偏倚值为-0.102067，偏倚百分率为90%；线性方程成立，差异有统计学意义（P=0.001），因此该实验组为线性偏倚，实际使用该量器时，可根据偏倚的线性回归拟合方程y（偏倚）=-0.008250x（参考值）-0.05257 计算出偏倚值，然后对测量结果进行修正。

由于d 组实验的整体偏倚值为-0.0721333，整体偏倚百分率为60%，其在2 mL、6 mL、10 mL均存在偏倚；同时线性回归斜率差异有统计学意义（P=0.007），线性方程成立。故d 组实验为线性偏倚，可根据方程y=-0.006075x-0.03568 对实际的测量结果进行修正。

在e 组实验中2 mL、6 mL、10 mL 处对应P值分别为0.698、0.068、0.933，整体偏倚对应P值0.182，差异均无统计学意义，说明10 mL 吸管量取时未发生偏倚。见图1、表4。

图1 量器线性与偏倚分析

表4 量器线性与偏倚分析

移液器与枪头的组合实验全部存在偏倚，其中1 号移液器搭配不同的枪头均不能建立线性关系，故1 号移液器不能通过线性方程对其发生的偏倚进行修正。2 号移液器搭配不同的枪头的组合同样全部存在偏倚，但同时可通过各自建立的线性关系方程对其偏倚进行修正。以上说明不同枪头（吸液嘴）对移液器的量取结果存在影响，而同一厂家移液器与枪头组合的量取结果优于不同厂家的组合。这与罗志东［8］的研究结果一致。

吸管与吸球的组合则均无偏倚，且在量取2 mL、6 mL、10 mL 液体时的平均值在所有组合中也最接近真值，故作为进一步优化的量器。

2.2 吸管变异源分析

2.2.1 吸管单因素分析 不同人员操作相同吸管的实验结果见表5。由统计数据可以得出，实验人员1与实验人员2的平均值与真值（10.000 mL）相差不明显；同时根据平均值标准误、标准差、变异系数及中位数分析，实验人员1的结果优于实验人员2，这与实际情况相符（实验人员1多年操作吸管，而实验人员2的经验相对较少）。而由配对t检验可知，差异无统计学意义（t=-1.36,P=0.244），表明不同实验人员使用相同吸管量取液体的结果虽有差异但不显著。

表5 描述性统计表

2.2.2 吸管双因素交叉设计分析 由表6 结果可知。吸球间的差异无统计学意义（F吸球=0.008,P吸球=0.928＞0.05）；吸管间的差异有统计学意义（F吸管=11.312,P吸管=0.004＜0.05）；同时由图2 可见，影响吸管双因素交叉实验的差异主要来自吸管（分差分量51.5%）和随机误差（分差分量48.5%）。以上数据说明在使用吸管量取液体时，不同的吸球不会对吸管的量取结果产生显著影响，而使用不同的吸管则对量取结果影响显著。同时随机误差也是显著影响吸管量取效果的重要因素，应在实际的操作中分析并优化。

2.2.3 吸管双因素嵌套设计分析 图3 中实验人员多变异图的平均值连线呈平滑趋势，说明实验人员及实验次数这两个变异源对测量值影响不显著。同时由表7 可知，不同实验人员间差异不显著（F实验人员=3.258,P实验人员=0.049≈0.05）；实验次数间差异无统计学意义（F实验次数=0.029,P实验次数=0.971＞0.05）。因此可以判断，不同的操作人员、操作批次对同一量器（吸球与10 mL 吸管的组合）量取10 mL 液体的结果无明显的影响，有良好的重复性和再现性。

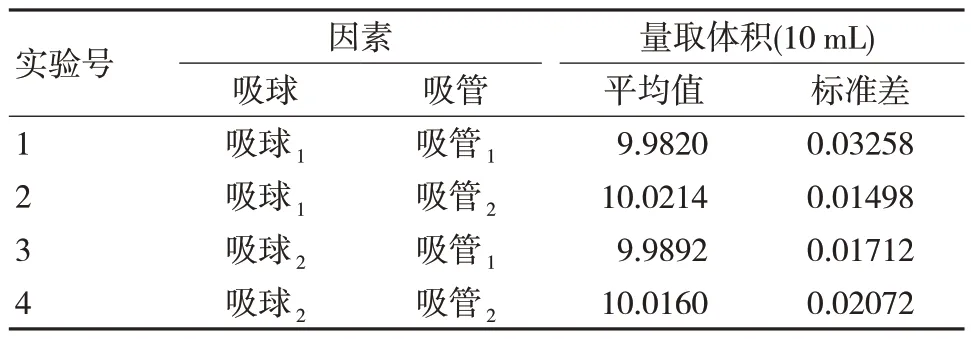
表6 吸管双因素交叉设计分析

图2 吸管量取值变异源的pareto 图

图3 测量值对于实验人员的多变异图

表7 吸管双因素嵌套设计分析

3 讨论

有研究者在采用称重法换算体积的说明中指出，在称重时要注意水的蒸发对称量结果的影响［9］。本文则是将注射用水由被测量器转移至干燥的一次性中管（每次实验前以相同条件烘干）后马上旋盖封口，同时放液操作也避免量器外壁的残留水影响称量结果。而称量用分析天平则通过计量确保结果的真实性。称量操作在压力、温度稳定且独立的称量间内进行，加之注射用水几乎无杂质的特性使其密度最大程度的接近1 g/mL。因此基于以上实验条件，保证用称量法能够有效的检测得到量器的实际量取体积。

根据量器线性与偏倚的分析结果，吸管较移液器的量取结果更接近真实值，移液器均发生偏倚有可能是使用频率高、日常维护不到位所造成。有学者指出日常操作方式和维护程度均会对移液器的量取结果造成影响［10-11］。不同吸管间的量取结果会存在差异，这主要是因为每根吸管在制造时很难做到完全一致，包括吸管直径、吸管嘴、刻度标识位置的一致性等。因此在量取一个目标体积时应始终使用同一吸管以减少差异。而使用吸管时产生的随机误差则需要进一步在实际操作中逐步分析、优化，并制定有效的控制措施。