气液针栓喷注器在节流水平下的雾化角模型分析

张波涛，李 平，杨宝娥

(1.西安航天动力研究所液体火箭发动机技术重点实验室，西安 710100；2.航天推进技术研究院，西安 710100)

0 引 言

在载人登月和深空探测等太空探索计划的驱动下，推力深度可调的变推力液体火箭发动机成为研究热点[1]。航天运输系统采用变推力发动机可以实现回收，星球探测器采用变推力发动机可实现软着陆，空间飞行器的对接采用变推力发动机可以改善机动灵活性，导弹采用变推力发动机可以提高机动性。

针栓喷注器是最具有代表性的可以改变喷注面积的喷注器，通过移动套筒改变喷注面积调节流量，从而使发动机实现大范围变推力的能力。针栓喷注器结构如图1所示，一种推进剂从中心通道进入喷注器，在针栓头部内壁面的作用下经过环缝或一系列孔径向喷出，另一种推进剂沿着中心筒外壁轴向流动，轴向推进剂与径向推进剂撞击后发生雾化，随后燃烧。与传统火箭发动机采用的几十个同轴式喷嘴和撞击式喷嘴相比，针栓喷注器具有独特的流场特性，在变推力下可以具有很高的燃烧效率(96%～99%)和固有的燃烧稳定性，已工程应用的针栓发动机还未发生过燃烧不稳定。同时绝大多数针栓发动机均采用一个喷注器，成本和重量大幅度降低[1]。

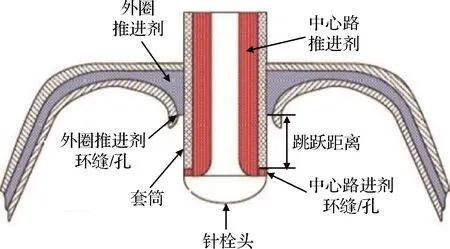
图1 针栓喷注器原理图

TRW公司从1960年开始对针栓喷注器进行研究[2]，最著名的阿波罗登月舱下降发动机(LMDE)将12名宇航员软着陆于月球，推力变比为10∶1。随后又研制了采用液氧煤油[3]、液氧液氢[4-5]、液氧甲烷[6]等无毒推进剂的针栓发动机。目前性能最高的变推力发动机为Space X的Merlin 1D发动机且成功实现重复使用。在进一步提高液液针栓发动机性能的同时，诺斯罗普·格鲁曼公司研制了液氢液氧膨胀循环的TR202气液针栓发动机[7]，推力变比为10∶1，喷注器结构如图2所示。国内在变推力火箭发动机领域的研究起步较晚，20 世纪70 年代开始进行针栓发动机的研究[8-9]，成功应用的针栓发动机为嫦娥三号和嫦娥四号使用的7500 N发动机[10-12]，此外中国还在开展电动泵压式变推力发动机[13]、80 kN液氧甲烷变推力发动机[14]的研制工作。目前国内外已成功飞行的针栓发动机均采用液液针栓喷注器，还没有掌握气液针栓喷注器的设计方法。

图2 TR-202喷注器[7]

前期TRW的研究经验表明雾化角是设计针栓喷注器最重要的参数[2]。由于针栓喷注器具有独特的流场特性，轴向推进剂和径向推进剂相撞后会产生上回流区和中心回流区，如图3所示。雾化角直接影响了针栓喷注器流场结构和雾场空间分布，是针栓喷注器设计过程中最重要的参数。Cheng等[15]通过建立轴向缝/径向缝型和轴向缝/径向孔型[16]液液针栓喷注器雾化角模型推导雾化角公式，分别为θ=arccos(1/(1+CTMR))和θ=arccos(1/(1+CLMR))，其中CTMR为动量比，CLMR为局部动量比，CLMR=CTMR/CBF，CBF为阻塞因子，定义为径向缝或所有孔周向长度之和与针栓周长之比。王凯等[17]在Cheng等[15]给出的雾化角基础上又引入变形因子C1和C2，即θ=arccos(1/(C1+C2·CTMR))，变形因子通过数值仿真或试验获得，因此预测公式准确度更高。Son等[18]通过对轴向缝/径向缝型液体中心的气液针栓喷注器试验结果拟合给出雾化角公式为θ=38.86(CTMR/We)-0.096。文献[19-20]通过对轴向缝/径向缝型液体中心的气液针栓喷注器雾化特性试验提出为了使针栓喷注器有好的雾化效果，喷注角度应尽量取大。Blakely等[21]通过对多径向孔液液针栓喷注器的试验结果拟合，给出雾化角公式为θ=C3arctan(C4·CLMR)(式中C3=0.7±0.05,C4=2.0±0.5)，并指出阻塞率对雾化角影响很小，雾化角主要受动量比的影响。王凯等[22]研究了数值仿真中壁面边界对雾化角的影响，指出两路推进剂均贴壁或均无贴壁时雾化角较准确，仅一路推进剂贴壁的结果误差较大。

图3 针栓喷注器流场结构

目前公开文献中关于针栓喷注器雾化角的研究均是关于非节流水平下的雾化角，针栓喷注器最显著的特点是通过移动套筒调节喷注面积以实现节流。因此，本文以气液针栓喷注器为研究对象，首先分析移动套筒调节喷注面积时对中心推进剂偏转角的影响，在此基础上建立节流水平下雾化角的理论模型，最后通过试验与数值仿真结果对雾化角模型进行校验，以获得准确性高的雾化角预测模型。

1 理论分析

1.1 中心推进剂偏转角理论模型

1.1.1基本假设

根据中心流体流动物理过程建立如图4所示的理论模型，作出如下假设(1)～(8)。

图4 中心推进剂偏转角示意图

(1)流动过程是稳态，与流动时间无关。

(2)将中心路流体分为两个控制体，分别为控制体1和控制体2，两个控制体交界面为流线水平方向位置。

(3)控制体边界由针栓喷注器几何参数决定，控制体1的上边界由中心筒壁厚和套筒遮挡喷注器出口距离决定，即γ1=arctan(Lsc/Tcb)，控制体2的下边界由针栓喷注器中心筒底端凹腔深度和内径决定，即γ2=arctan(Rib/Tpc)。

(4)控制体1的上边界流线和控制体2的下边界流线均以相同的线性速率k旋转，旋转到2个控制体界面相接。

(5)控制体1和控制体2在喷注器出口截面速度均为u。

(6)忽略体积力、表面张力、壁面对流体的摩擦力及环境气体对流体表面的剪切阻力。

(7)液体无相变，不考虑传热。

(8)轴向动量和径向动量均守恒。

1.1.2公式推导

由于流线以线性速率变化，可得：

γ1=ky1

(1)

γ2=ky2

(2)

对于任一控制体，在喷注器出口截面单位高度流量为：

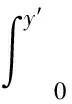
(3)

式中：ρ为中心路流体密度，u为出口截面速度，W为径向孔宽度。

控制体1在出口的径向动量为：

(4)

控制体1在出口的轴向动量为：

(5)

将y1=γ1/k代入式(4)和式(5)，得：

(6)

(7)

同理，控制体2径向动量和轴向动量分别为：

(8)

(9)

因此，根据轴向动量和径向动量守恒，偏转角为：

(10)

1.2 雾化角理论模型

1.2.1基本假设

根据液束与气膜撞击过程建立如图5所示的控制体几何模型，对液束中厚度为H的微元体进行分析，作出如下假设(1)～(6)。

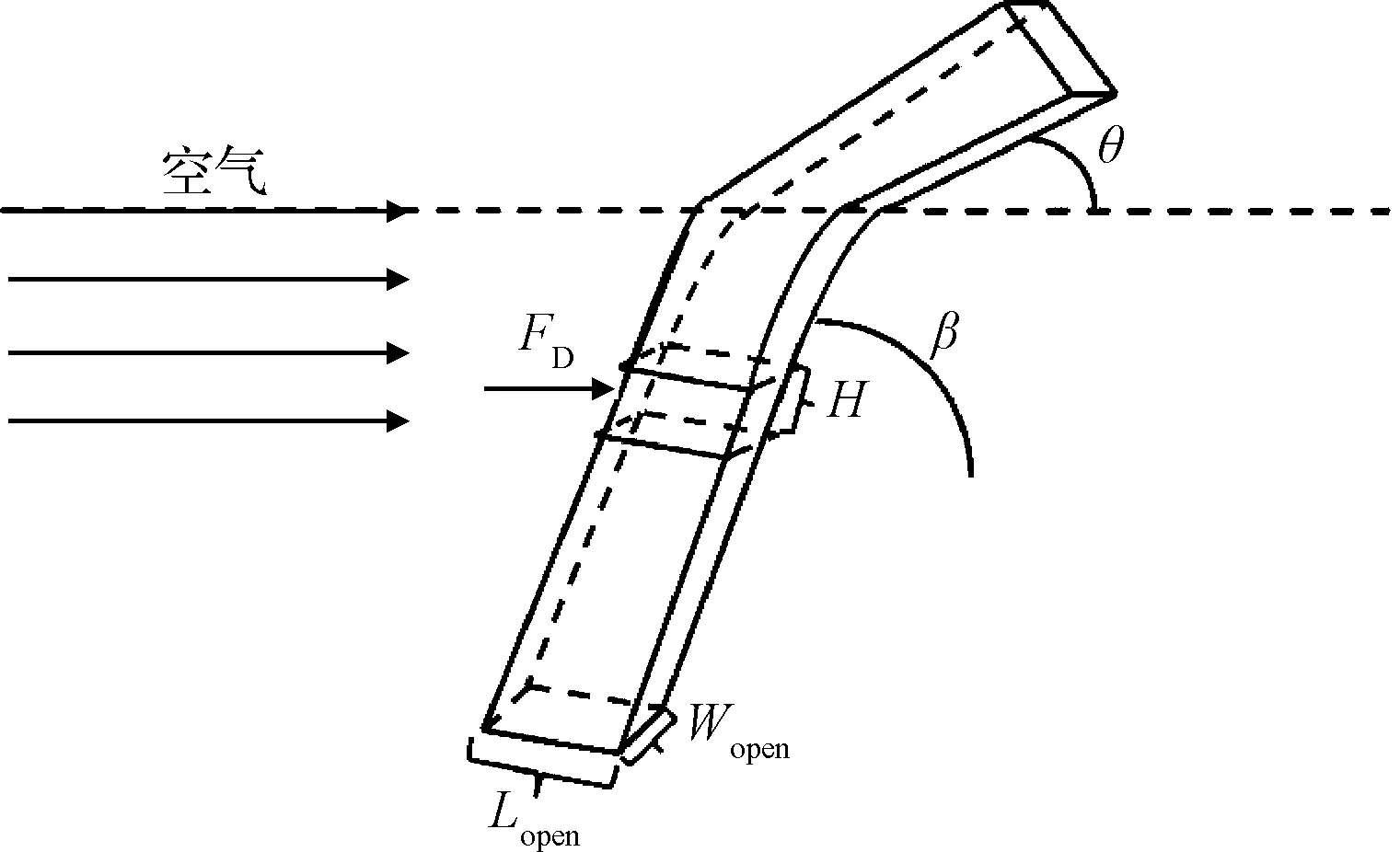
图5 液束撞击气膜雾化角示意图

(1)流动过程是稳态，与流动时间无关。

(2)液束在穿透气膜过程中不变形且无质量损失，液束横截面始终为矩形。

(3)液束喷出时具有速度ul和中心推进剂偏转角β。

(4)液束穿过气膜后在惯性作用下以直线运动。

(5)忽略体积力、表面张力、液束黏性力、壁面对流体的摩擦力及环境气体对流体表面的剪切阻力。

(6)液体无相变，不考虑传热。

1.2.2公式推导

轴向动量方程可表示为：

(11)

对式(11)进行时间积分可得：

(12)

由于ul=dx/dt，对式(12)进行积分，得：

(13)

根据假设，矩形液束在运动过程中不变形且速度保持恒定，将y=ulsinθt代入式(13)，得：

(14)

动量比定义为：

(15)

式中：L为径向矩形孔长度，W为径向矩形孔宽度，H为轴向气膜厚度。

将动量比代入式(14)，得液束微元轨迹为：

(16)

根据假设，液束微元运动至气膜厚度处穿过气膜且向右上方以直线射出，得到液束在高度H处的角度为：

(17)

2 试验系统与试验件

2.1 试验装置

动量比定义中包括了轴向气膜和径向液束的流量参数和结构参数，为了研究动量比对雾化角的影响规律，将试验件设计为可更换局部组件的方案。试验件主要由四部分组成，包括气体汇流组件、可更换的液路喷嘴组件、可更换的轴向气膜调节组件和中心液路喷嘴组成。为了使轴向气膜分布均匀，气体从对称的两个气体入口进入气体汇流组件内充分混合后从轴向环缝喷出。通过调节可更换的液路喷嘴组件长度和轴向气膜组件内径分别改变跳跃距离和轴向环缝高度。在初步研究中，为了掌握气液针栓喷注器单径向孔雾化特性且便于光学观测，在试验件中心液路喷嘴上设置两个对称的径向液束孔，如图6所示，试验件结构参数如表1所示。

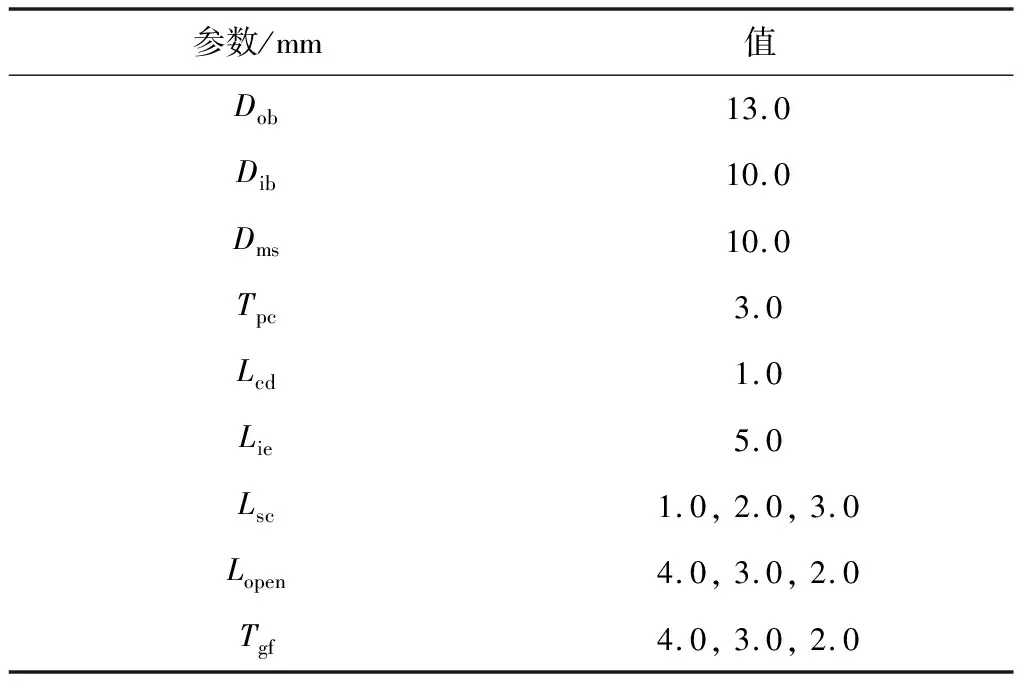
表1 气液针栓喷注器结构参数

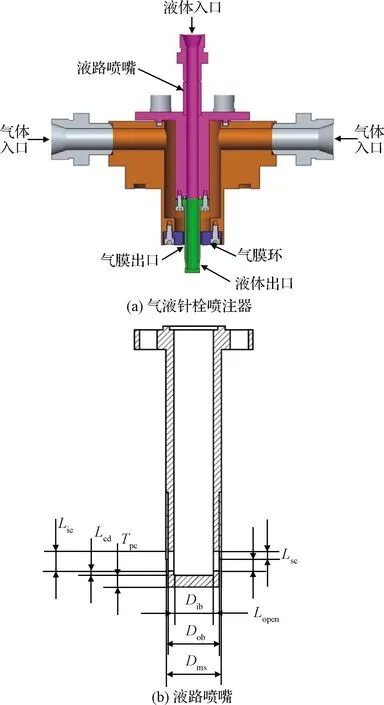
图6 气液针栓喷注器结构

对气液针栓喷注器在40%,60%和80%节流水平下的中心推进剂的偏转角和雾化角进行分析，轴向气膜厚度Tgf与径向液束出口高度Lopen根据节流水平线性调节。节流水平在40%，60%和80%时的径向液束出口高度分别为2 mm,3 mm和4 mm，当节流水平一定时，径向液束出口高度等于轴向气膜厚度。表2和表3分别为中心推进剂偏转角和雾化角的工况参数，文中TL符号代表节流水平。

表2 中心推进剂偏转角试验工况

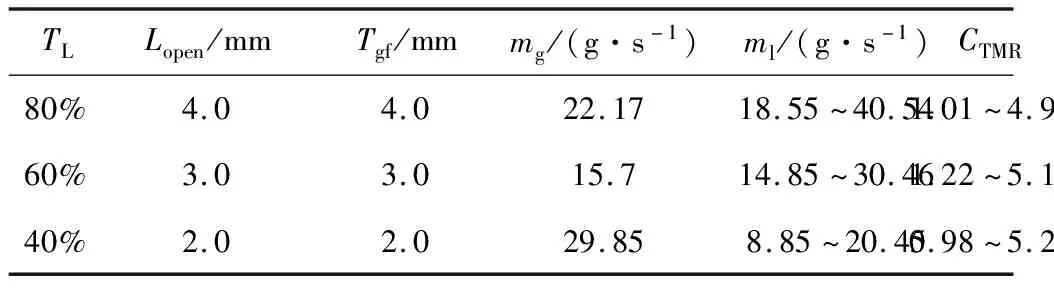
表3 雾化角试验工况

2.2 试验系统

试验系统包括管路供应系统、测量系统和台架系统，如图7所示。管路供应系统包括贮箱和高压气源等，测量系统包括压力传感器和科氏流量计等，台架系统包括支架和收集槽。在雾场的一端使用LED光源照亮雾场，另一端采用Phantom V12.1型号的黑白高速相机拍摄气液针栓喷注器的雾化过程。试验采用的拍摄频率为3000 Hz，曝光时间为15 μs，图像像素分辨率为640×480。

图7 雾化试验系统

2.3 图像处理方法

中心推进剂偏转角和雾化角的试验测量方法相同，由于气液针栓喷注器的雾化过程是瞬态的，试验中的中心推进剂偏转角和雾化角会随时间产生波动。为了采用统一的标准精确测量中心推进剂偏转角和雾化角，对高速摄影拍摄的雾场图像进行处理，以雾化角图像处理过程为例，图像处理过程如图8所示，图8(a)为原始瞬态图像，首先对其进行增强处理，获得增强后的图像，如图8(b)所示，接着对1000张增强后的图像平均处理，获得如图8(c)所示的平均图像。最后在平均图像上测量喷雾扇边界，为了防止拍摄和加工误差，在图像上测量θ1和θ2两个雾化角，最终结果取两个雾化角的平均值，如图9所示。

图8 图像处理过程

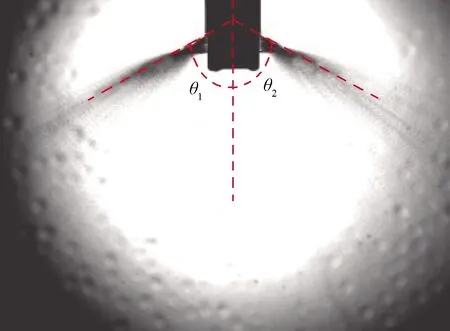
图9 试验雾化角

3 数学物理模型

3.1 控制方程

对于针栓喷注器，中心路流体流动为低速流，因此液相与环境气体均可视为不可压流，在计算过程中假定气液两相流动过程是等温的，且不考虑液相蒸发过程，因此无需求解能量方程，求解两相流的流动控制方程如式(18)～(20)所示。

连续方程：

(18)

动量方程:

(19)

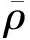
(20)

3.2 CLSVOF方法

采用经典的CLSVOF方法(Coupled Level-Set and Volume-of-Fluid Method)捕捉气液两相界面，CLSVOF方法结合了VOF方法和Level-Set方法的优缺点，以克服VOF方法在空间上不连续和Level-Set方法容易出现流体体积不守恒的缺陷。

在VOF方法中，两相界面被定义为液相在网格里的体积分数，控制方程为：

(21)

式中：t为时间，v为速度；α=0表示网格里为气相，α=1表示网格里为液相，0<α<1表示网格存在气液两相。

界面位置和时间演化方程由Level-Set方法定义：

(22)

式中：φ为到气液两相界面的距离函数。

距离函数φ为：

(23)

式中：L为x到气液两相界面的距离,Ω1和Ω2分别表示气、液所处区域,Γ为气液两相界面。

为了避免界面附近密度比和黏度比较大引起的数值不稳定，采用Heaviside函数光滑气液两相界面的密度和黏度，Heaviside方程可表示为：

(24)

式中：w=1.5h，h为网格尺寸。

对于两相流动，密度和黏度定义为：

ρ(φ)=ρg+(ρl-ρg)H(φ)

(25)

μ(φ)=μg+(μl-μg)H(φ)

(26)

3.3 湍流模型

为精细捕捉液束和气膜相互作用产生的湍流结构，采用模拟应力混合SBES(Stress-Blended Eddy Simulation)方法[23]，在近壁面采用雷诺平均数值模拟(Reynolds average numerical simulation, RANS)，在湍流核心区采用大涡模拟(Large eddy simulation，LES)，以保证大尺度湍流脉动被直接求解。应力混合形式为

(27)

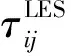
(28)

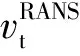
(29)

(30)

式(28)～式(30)中各项含义详见文献[24-25]。

3.4 计算模型

由于物理模型的流场具有对称性的特征，因此数值仿真对物理模型的1/4区域进行计算，将对称面设置为对称面边界条件，计算域为圆柱形，数值仿真中的模型尺寸与试验件一致，计算域径向半径为27 mm，在轴向方向上从针栓端头到轴向出口的长度为3 mm,如图10所示。在数值计算中心推进剂偏转角时，将气体入口设置为壁面边界条件。计算域初始网格约为600万，为了提高捕捉气液界面精度，使用网格自适应加密技术对网格进行加密。

图10 计算域示意图

4 讨论与分析

4.1 中心推进剂偏转角

图11给出了不同节流水平下的中心推进剂喷射图像。根据理论分析，中心推进剂的偏转角主要取决于几何参数，如式(10)所示。为了全面分析几何参数和工作条件对中心推进剂偏转角的影响，绘制了试验、数值仿真和理论预测的中心推进剂偏转角与节流水平、喷射压降之间的关系图，如图12所示。当喷射压降一定时，中心推进剂偏转角会随着节流水平的降低而显著减小。当节流水平恒定时，中心推进剂偏转角随压降的增加而略有增加。可以看出，在较宽的喷注压降范围内，数值模拟和试验获得的中心推进剂偏转角与本文模型预测结果吻合良好，说明理论预测结果误差很小。

图11 不同工况下的中心推进剂偏转角图像

图12 不同压降和节流水平的中心推进剂偏转角

4.2 雾化角

图13给出了不同节流水平下的雾场图像，从图中可以看出当节流水平一定时，雾化角随着动量比增加而增大。当动量比一定时，雾化角随着节流水平降低而减小。从试验结果可以看出液束与气膜撞击后快速变形。通过数值结果进一步分析液束横截面变形过程，图14给出了节流水平为60%时动量比为2.5的液束横截面变形过程，由于移动套筒和气膜初始厚度分别为0.5 mm和3 mm，图中的截面为液束喷出后在径向0 mm,0.5 mm,1.5 mm,2.5 mm和3.5 mm处的液相分布。径向液束在轴向气膜正压和侧面剪切的双重作用下变形，液束喷出后迎风面向两侧运动，横截面先发展为“T”形，最后迎风面和背风面逐渐接近并展向拉伸为膜状。

图13 不同工况下的中心推进剂偏转角图像

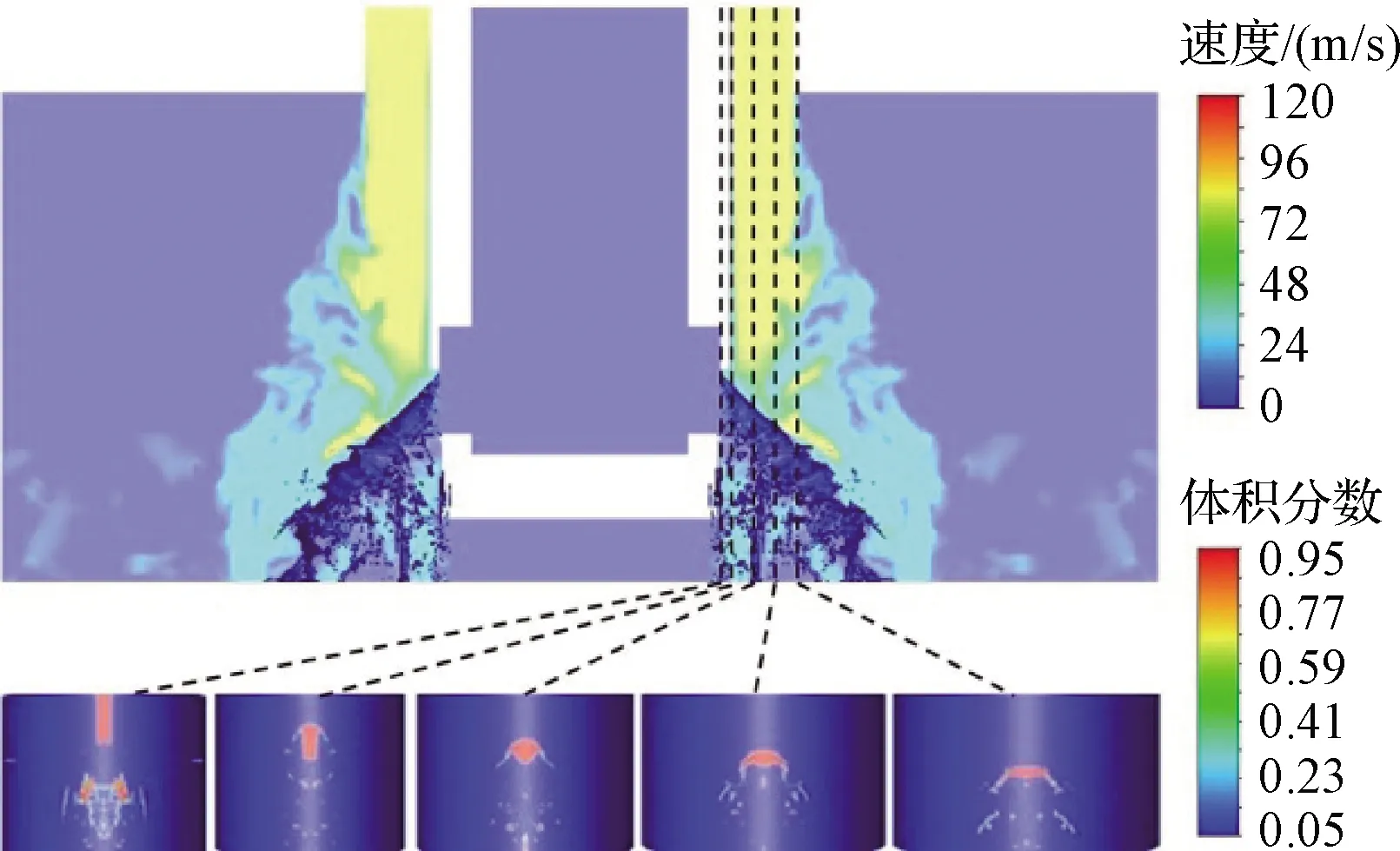
图14 液束横截面变形过程

根据试验结果和数值结果可以看出液束与气膜撞击后会快速变形，液束实际动量会小于初始动量，而雾化角理论模型中假设液束不变形，因此对雾化角理论模型中推导的式(17)进行修正，通过试验结果获得雾化角修正系数C，修正的雾化角公式为式(31)。对于不同节流条件下的雾化角，当动量比为0～5时，C的总体平均值为0.8，总体标准差为4.99%。根据理论分析，雾化角主要由动量比和中心推进剂偏转角决定，中心推进剂偏转角由节流条件决定。因此，不同节流条件下试验、数值计算和理论预测雾化角随动量比的变化如图15所示，可以看出试验雾化角、数值计算雾化角和理论预测雾化角吻合很好，说明了雾化角主要受节流条件和动量比影响。

图15 不同动量比和节流水平下的雾化角

(31)

5 结 论

为了研究节流水平对气液针栓喷注器雾化角的影响规律，从动量守恒出发建立了气液针栓喷注器在节流水平下的雾化角理论模型，同时采用CLSVOF方法、网格自适应加密方法和SBES湍流方法对其进行了数值模拟，并通过试验结果对理论模型进行校验，主要结论如下：

1)通过理论推导建立了气液针栓喷注器在节流水平下的中心推进剂偏转角理论模型，理论预测值与数值计算和试验结果均吻合很好，说明中心推进剂偏转角主要受几何参数影响，工况参数对其影响很小。

2)基于中心推进剂初始偏转角，通过理论推导建立了气液针栓喷注器在节流水平下的雾化角理论模型。由于液束与气膜撞击后有效动量减小，因此在理论预测公式中引入变形因子C，根据试验结果获得变形因子为C=0.8，引入变形因子的理论模型预测值和试验及数值模拟结果吻合很好。

3)当节流水平一定时，雾化角随着动量比增加而增大。当动量比一定时，雾化角随着节流水平降低而减小。雾化角主要受动量比和节流水平决定，其他工况参数和几何参数都是通过影响动量比和中心推进剂偏转角而间接影响雾化角。

致 谢

感谢国家重点基础研究发展计划和国家自然科学基金的资助以及液体火箭发动机技术重点实验室杨岸龙博士在试验方面的大力支持。