多项式插值法在水位推测中的应用

王 朝，郭志勇

（中交第一航务工程勘察设计院有限公司，天津 300222）

引 言

水位对水深测量起决定性的作用，水位的准确性直接关系到水深测量的精度，是水深测量的基础。水域中其他水位站通常会通过近岸水位站进行传递和换算，因此近岸水位数据的准确性很重要。目前，对近岸水位观测的方法主要为人工水尺观测、验潮井验潮仪和压力式验潮仪。人工水尺观测是对一定短时间内的连续读取的多次水位数据取平均值作为此时刻的水位值，人工多次观测取均值对瞬时水位变化起到一定的滤波作用，水位数据不会出现较大的异常值，人工观测会受到海况、天气、观测者的主观因素以及水尺的标定等制约条件，同时对验潮基准也要进行定期检查；验潮井底部的出入水管道起到的阻尼作用能够有效的进行滤波，水位数据变化平滑，无异常水位数据，验潮井内的设备需要定期的进行维护和校对，不然对水位观测存在时差和精度方面的问题，同时验潮井造价高，受到有关部门的管理，在使用通用性方面受到一定的制约；压力式验潮仪便携、精度高，使用前需要注意仪器的时间设置、校准和比对，验潮仪可以设置一定时间内（30～60 s）滤波，获得此时刻潮位数据，但是固定滤波周期的数字滤波不是根据实际海况进行选择的，观测水位数据存在异常变化的可能性比较大，因此对验潮仪的观测数据需要进行检查和必要的滤波处理[1,2]。

对水位逐时数据推测方面，许多学者进行了研究，并提出了一定的有效方法。孙维康[3]使用了二次抛物线拟合法、自报值循环逼近法和参数法对水位数据进行推测，对缺测的水位进行补齐，三种方法对水位数据都能够进行有效的推算，并满足海道测量规范要求。自报值循环逼近法较二次抛物线拟合法和参数法的精度较低，二次抛物线拟合法简便，不受验潮站潮汐性质的影响，在非大潮和非小潮期间数据效果较好，参数法不受水位数据时长的限制，水位推算准确程度高，但是需要相关性较强的两个相邻同步验潮站的资料[4,5]。对水位数据的判断可以看作水位数据粗大误差的判读，熊艳艳[6]研究了四种常用的判别准则，对粗大误差数据进行有效剔除，罗俐雅[7]把使用符合样本数较多且服从正态分布的拉伊达准则和肖维勒准则进行检验，并取得了较好的结果。

水位曲线是连续光滑的曲线，使用二次抛物线拟合法和多项式插值法对验潮仪获得的水位数据进行逐时拟合，通过拟合数据和实测水位数据比较，运用拉伊达准则和肖维勒准则进行判断推测水位数据。

1 方法原理

1.1 水位推算方法

方程组的矩阵形式为：

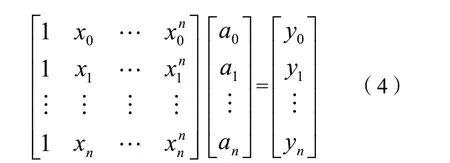
方程组的系数矩阵为范德蒙德（Vandermonde）行列式，且方程组有唯一解。使用范德蒙德行列式计算公式和克拉默法则可以求得方程组的解，即函数 )(xfy= 的参数值 naaa ,,,10… 。

文献[8]通过已知点拟合未知点，可以把已知点加权平均后表达未知点，通过加权系数表示已知点对未知点的影响程度，则表达式有：

方程组的矩阵形式为：

使用范德蒙德行列式计算公式和克拉默法则可以求得方程组的唯一解：

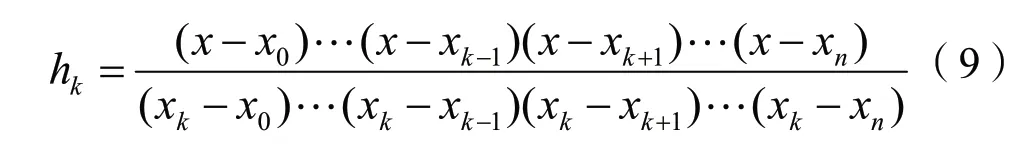
未知点函数表达式为：

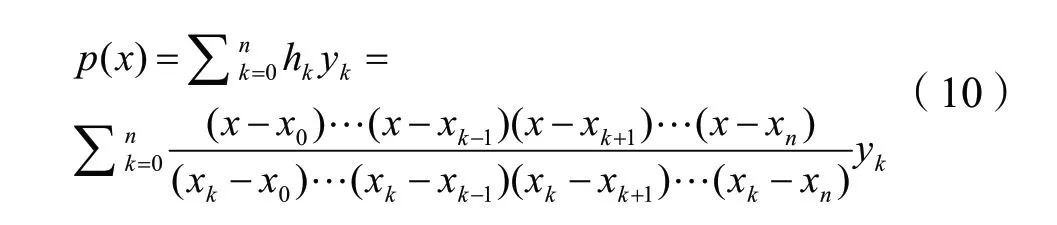
从以上过程可以看出，加权平均法具有一定的物理意义，同时在计算过程公式形式更规范化，使单参数的计算过程更简单。

1.2 异常数据判别方法[7]

数据判别使用的拉伊达准则和肖维勒准则都是基于样本服从正态分布的假定。

1）拉伊达准则

第i 个推算的潮位数据为xi，实测的水位数据为hi，则误差方程为：

2）肖维勒准则

由正态分布概率计算公式得：

已知样本数N，根据公式（13）、（15）计算限差ZS，判读推测数据的异常值。

2 水位数据推算

本文使用缅甸仰光河，距入海口约25 km 处的验潮仪水位数据。由于受到海水的潮汐作用，河水的水位有潮汐变换情况，为规则半日潮，同时受到河水流动的作用力，水位曲线会受到一定的影响。

选用2019 年11 月17 日0:00 至23:55 的验潮仪水位数据，数据间隔为5 分钟，共288 个水位数据，并通过水文专业处理，保证数据的正确性。对数据分别使用二次抛物线拟合和多项式加权插值的方法，进行逐时水位数据的推算，多项式加权插值法选用三个已知点，拟合中间点的水位数据，被拟合点分别从前、后两个方向进行拟合，取平均值作为该点的最终拟合值。最后，应用拉伊达准则和肖维勒准则对推算的水位数据进行判断。推算水位数据的结果如表1。

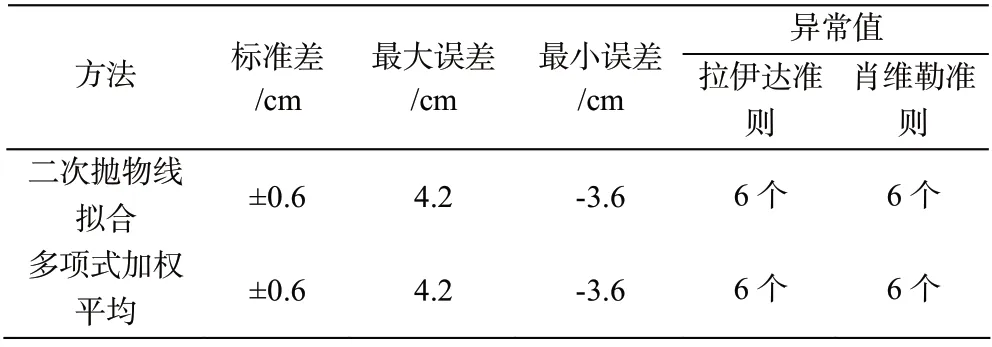
表1 推算水位数据结果

从拟合插值的方法可以看出，被拟合点都是由相邻点进行拟合和推算的，因此使用上面两个方法对数据列的开始和结尾的两个数据不能拟合，造成数据的浪费。因此，使用多项式外推的方法，即通过三个已知点拟合曲线的趋势，对未知点进行推算。使用多项式加权平均法外推水位数据的结果，见表2。

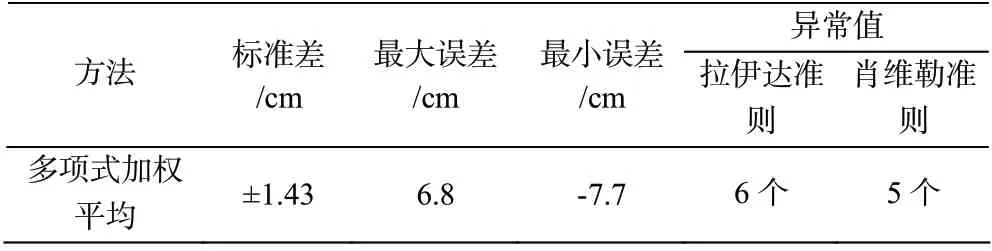
表2 外推水位数据结果

3 结果对比分析

从以上数据结果可以看出，二次抛物线拟合法和多项式加权插值法对水位的推算都能够有效的计算。多项式加权平均法对于外推的数据标准差和误差都比较大，原因是外推的未知点可能和已知点的趋势不同。拉伊达准则限差为3S，肖维勒准则为ZS，通过样本数计算的Z 取值为3.12，两种准则对异常值判断除去后的推算水位数据能够保证在 5 cm 的误差范围内。

由表1 可以看出，二次抛物线拟合法和多项式加权平均内插法得到的数据精度高，剔除异常值后的数据能够保证在2 cm 的误差范围内。两种方法的标准差、最大误差和最小误差都相同，甚至异常值的个数和位置也都一样，原因是：使用的多项式是函数次数为二次的三阶多项式，与二次抛物线有极大的相似关系。被推算值都是根据相邻数据进行解算，被推算数据的结果受已知值的影响程度很大。

为进一步验证多项式加权平均插值法的适用性，将多项式扩展到四阶三次多项式，对水位数据进行拟合内插推算后的结果，见表3。

表3 水位数据拟合内插推算结果

对二次抛物线拟合、三阶二次多项式和四阶三次多项式计算的误差ri剔除异常数据后的统计结果见表4。

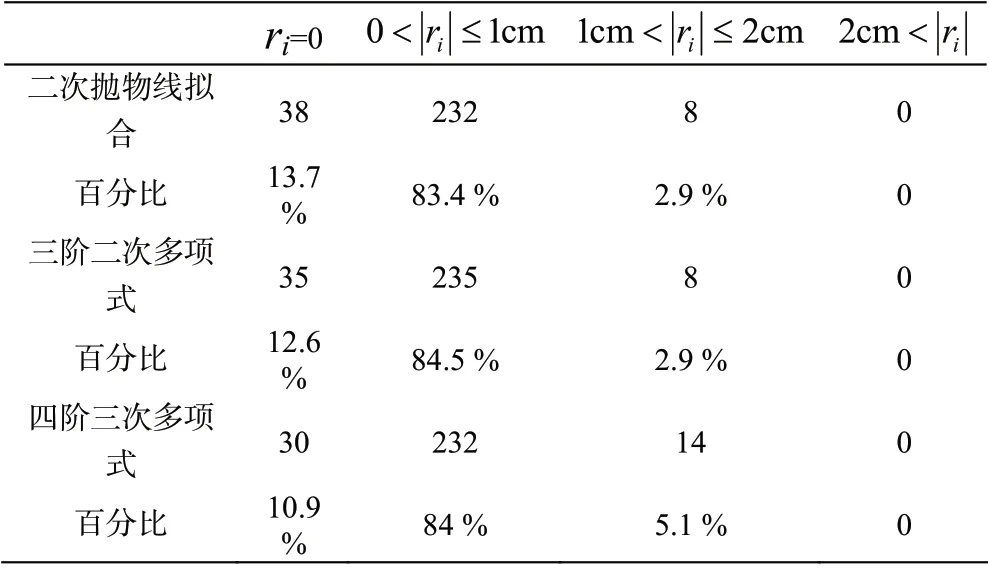
表4 剔除异常数据后的统计结果

从以上数据可以得出，二次抛物线拟合、三阶二次多项式和四阶三次多项式对水位数据都能够进行有效推算，其中二次抛物线拟合、三阶二次多项式解算结果相当。

4 结 语

本文使用二次抛物线拟合、三阶二次多项式和四阶三次多项式对水位数据进行了推算，结果数据表明三种方法都能够进行有效的计算，结果数据的误差都在2 cm 内，其中二次抛物线拟合法和三阶二次多项式加权内插法的结果最好。从方法上来看，推算的数据受已知数据的影响程度较大，所以在使用拟合前需对数据进行检查和滤波，使用多项式加权平均法需要对阶数的选取进行判断。拉伊达准则和肖维勒准则的最终限差分别为3S 和ZS，Z与样本数有密切的关系，当Z 小于190 时，肖维勒准则判读会更加准确[7]。本文只使用了一次计算，下一步需要对数据进行剔除异常值后，进行迭代计算，进一步验证方法的可靠性。