高桩码头桩后回淤对桩的影响数值分析

张振超，李慧娣

（1.中航天建设工程集团有限公司，北京 100071；2.中国建筑技术集团有限公司，北京 100013）

引 言

高桩码头主要由上部结构的面板和面板下的桩基础两部分组成。面板构成码头的地面，并把桩基础连成整体，直接承受作用在码头上的水平力和垂直力，并把他们传给桩基础，桩基础再将这些力传给地基。高桩码头适用于软土地基，具有透空性好、结构轻、减弱波浪效果强、砂石料用量省，且适用于多种工程地质条件等优点，因而被广泛地应用于实际工程中[1]。

高桩码头在使用过程中水下泥沙会发生淤 积[2]，很多高桩码头在建成后10 年之内即会出现破损现象，甚至无法正常使用，据我国对使用7～25年的高桩码头进行的抽查，结果发现，有损坏或严重损坏的比例高达89 %[3]。高桩码头破坏的原因是多方面的，是各种因素综合作用的结果，其中码头水下泥沙淤积的影响是一个重要的但却被忽视的因素[4]。

实际工程中，高桩码头桩后沿淤泥回淤一直是影响结构安全的突出问题[5-6]，对码头回淤状况进行现场勘测也往往受海况、成本等因素制约，面临着许多现实的困难和挑战。而对淤泥质高桩码头淤泥回淤进行数值模拟研究[7]，不仅会节省大量的成本，还可以针对极端海况下水下岸淤泥回淤强度进行模拟预报，这对于桩基的设计具有重要的指导意义。

已有的国内外文献往往单独考虑码头水下岸坡泥沙的主要来源及冲淤总趋势、淤泥回淤率以及回淤强度、港口淤泥回淤的计算方法等问题[8-11]，对于高桩码头后沿回淤分析尚未见报导。本文的出发点相对而言比较新颖。鉴于此，本文以某国际集装箱码头为例，建立了高桩码头与土相互作用的非线性三维有限元数值模型，分析了高桩码头桩后回淤前后对码头结构的影响。

1 ABAQUS 有限元分析软件

ABAQUS 以其丰富的、可模拟任意几何形状的单元库以及强大的计算功能，在结构与土相互作用的领域得到了广泛的应用。

在有限元分析过程中，土是岩石风化而成的碎散颗粒的集合体，其本构模型即应力应变关系十分复杂。弹性本构模型主要有：线弹性模型、非线性弹性模型（如邓肯一张双曲线模型）、高阶的非线性弹性理论模型。弹塑性本构模型主要有：Mohr-Coulomb 模型、剑桥模型、莱特—邓肯模型、清华弹塑性模型等。每种本构模型均定义或隐含了各自的屈服准则或破坏准则、硬化准则及流动法则。

在以上几种弹塑性模型中，Mohr-Coulomb模型可以考虑材料等向应变硬化和软化特性，能较好地描述岩土类材料的材料特性，且参数少，使用方便，在岩土工程界得到了广泛的应用，因此本文土体选用Mohr-Coulomb模型进行分析。

在简单应力状态下，Mohr-Coulomb屈服准则表示为：

式中：1σ 、2σ 和3σ 分别表示第一、第二和第三主应力；c 和φ 分别表示粘聚力和内摩擦角。

2 工程概况及有限元模型

2.1 工程概况

码头结构采用高桩梁板式结构，排架间距 10.5 m。上部结构均为现浇桩帽节点，预制横梁和纵向梁系，预制现浇叠合面板结构。由于本工程区域地质条件十分复杂，其中第15 分段为全直桩，码头桩基采用嵌岩桩，每榀排架布置7 根φ2 300 mm 嵌岩桩。图1 为码头断面（第15 分段）。

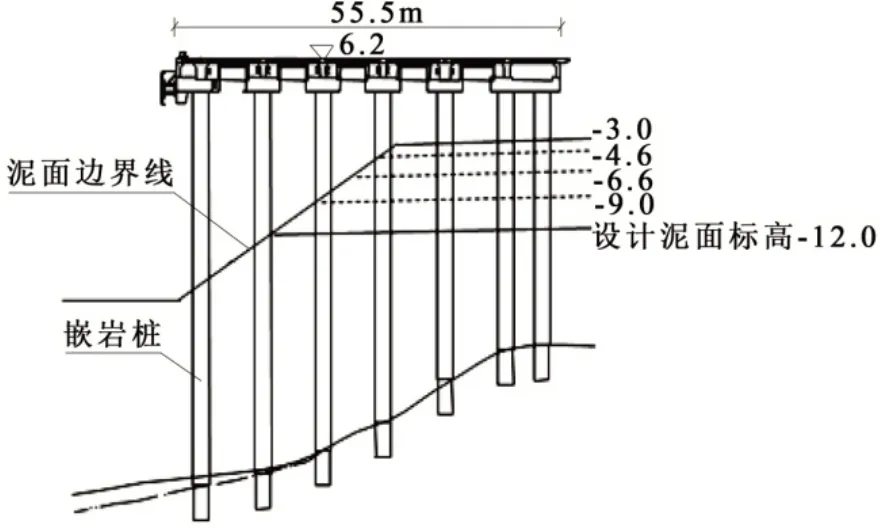
图1 码头断面（第15 分段，1#泊位）

根据相关研究成果，水下岸坡淤积对码头结构有重要影响。为了解码头水下岸坡淤积情况及为后续分析淤积体对本工程码头结构影响进行计算提供依据，对码头水下地形资料进行了分析整理。码头从开建之初至今，对码头后方的水下地形进行了多次测量。各次测量的观测时间及对应码头后沿水深详见表1。

表1 码头后沿水深历次观测结果

根据码头后沿水深历年观测结果，从2003 年6月至2015 年1 月，对桩后淤泥回淤厚度分为5 种情况，分别为：

1）2003 年6 月，泥面高程为-12 m，淤泥不存在；

2）2006 年8 月，泥面高程为-9 m，淤泥回淤厚度为3 m；

3）2008 年10 月，泥面高程为-6.6 m，淤泥回淤厚度为5.4 m；

4）2012 年5 月，泥面高程为-4.6 m，淤泥回淤厚度为7.4 m；

5）2015 年1 月，泥面高程为-3 m，淤泥回淤厚度为9 m。

2.2 有限元模型

建立一榀排架有限元模型，如图2 所示。模型中桩径2.3 m，桩长50 m。土为均质土层，将其简化为6 层。由于桩的刚度远大于桩周土体的强度，当桩周土体强度超过屈服极限进入弹塑性阶段时，桩基通常仍处于弹性变形阶段。因此桩体和承台所用混凝土材料采用理想弹性模型，土体采用Mohr-coulomb 准则的弹塑性模型。土层基本参数基于实际工程测得的土体力学性能指标，桩和土的参数如表2 所示。

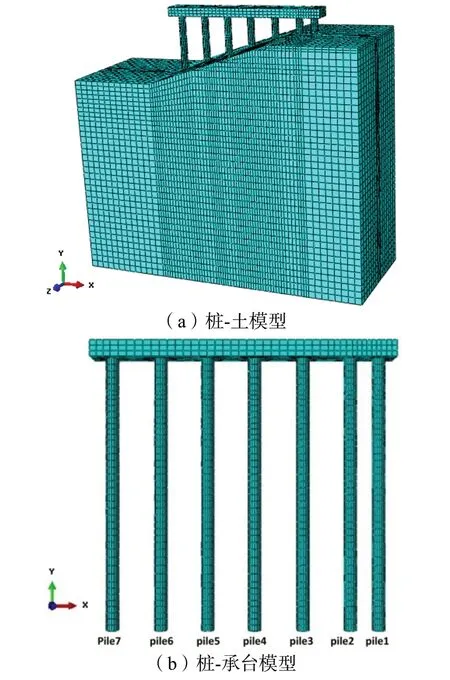
图2 有限元模型

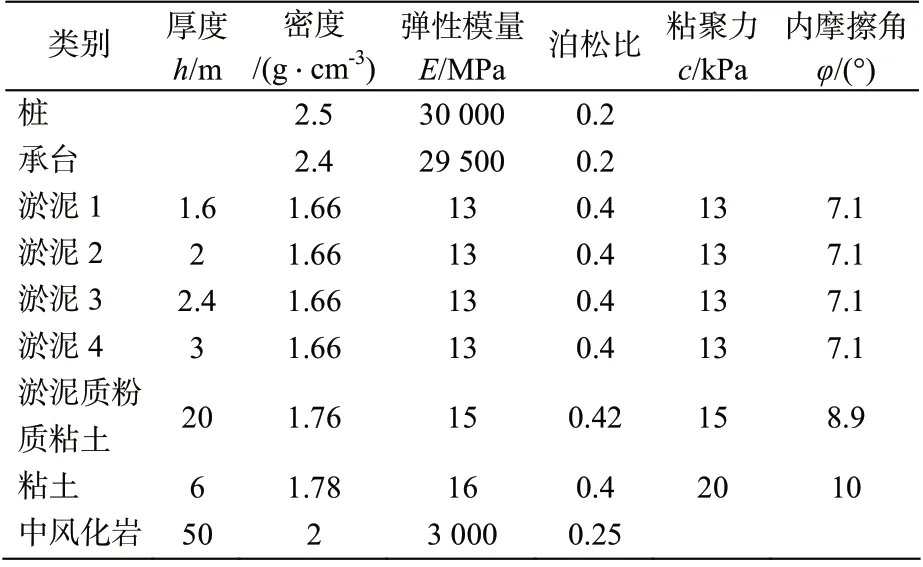
表2 桩土参数

计算模型靠岸侧以及靠海侧边界对x、z 方向均约束，模型底部对x、y、z 方向均约束。在桩与桩周土之间设置滑动接触面，模拟桩与土的相互作用。模型共67 402 个节点，共60 707 个单元。码头结构和土体单元全部采用八节点减缩积分单元C3D8R。

水平荷载为36 kN，竖向荷载为135 kN。水平荷载以均布力的形式施加在承台边上，方向为垂直于排列方向。竖向荷载以均布力的形式施加在承台上，方向与桩身方向一致。如图3 所示。

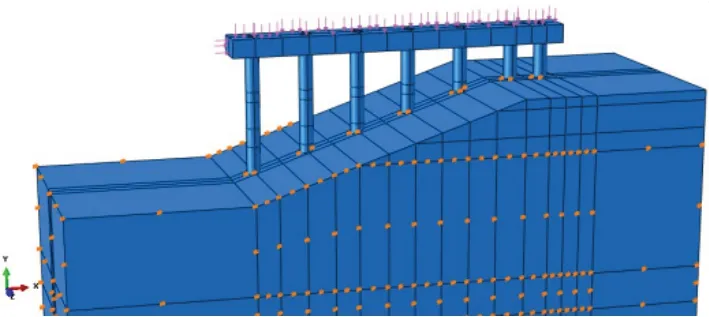
图3 单排超长桩模型受力

3 计算结果分析

3.1 泥面高程为-12 m 时桩基最大主应力的分布

图4 表示泥面高程为-12 m 时桩基最大主应力分布，该情况下桩基最大主应力的模拟结果和实际检测结果相符合。

根据原设计单位提供高桩码头资料，其混凝土水下开裂拉应力为11.288 MPa。由图4 可以看出，在泥面高程为-12 m 时，桩基最大主应力均满足抗裂要求。

图4 泥面高程-12 m 时桩基最大主应力分布

3.2 泥面高程为-9 m 时桩基最大主应力的分布

图5 表示泥面高程为-9 m 时桩基最大主应力分布。当回淤深度为3 m 时，pile1～pile7 的桩基最大主应力值较原设计状态增大。此时，pile6 和pile7的最大拉应力已经非常接近结构的开裂应力。

另外，由图5 可以看出，桩基拉应力最大值出现在距离桩顶2 m 位置处。且在距离桩顶0～2 m 时，桩基最大拉应力逐渐增大，当大于2 m 时，距离桩顶越远，桩基最大拉应力逐渐减小。

在距离桩顶41 m 位置，桩基最大拉应力较初始状态增大。此位置与桩基接触的土层为中风化岩。

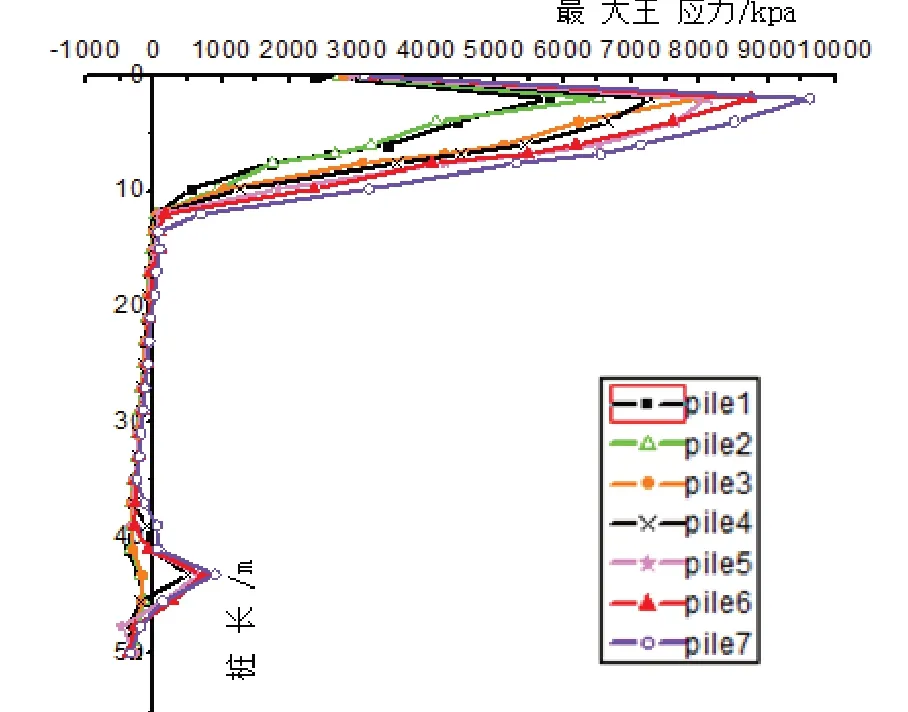
图5 泥面高程-9 m 时桩基最大主应力分布

3.3 泥面高程为-6.6 m 时桩基最大主应力的分布

图6 表示泥面高程为-6.6 m 时桩基最大主应力分布。当回淤深度为5.4 m 时，对比图5、图6 可以看出，pile1～pile7 的桩基拉应力最大值增大，且在距离桩顶2 m 位置处，pile4～pile7 的拉应力最大值大于抗裂应力，桩基拉应力已不能满足抗裂要求，结构开裂。

图6 泥面高程-6.6 m 时桩基最大主应力分布

3.4 泥面高程为-4.6 m 时桩基最大主应力的分布

图7 表示泥面高程为-4.6 m 时桩基最大主应力分布。当回淤深度为7.4 m 时，对比图6、图7 可以看出，pile1～pile7 的桩基拉应力最大值增大。在距离桩顶2 m 位置处，pile3～pile7 的最大拉应力值大于抗裂应力，桩基拉应力已不能满足抗裂要求，结构开裂。另外，在距离桩顶41 m 位置处，桩基最大拉应力也明显增大。所以，随着回淤深度的增加，桩基最大拉应力值呈现增大的趋势，使得桩基拉应力不能满足抗裂要求，结构开裂。

图7 泥面高程-4.6 m 时桩基最大主应力分布

3.5 泥面高程为-3 m 时桩基最大主应力的分布

图8 表示泥面高程为-3 m 时桩基最大主应力分布。当回淤深度为9 m 时，对比图7、图8 可以看出，桩基拉应力最大值明显增大，在距离桩顶2 m位置处，pile1～pile7 的最大拉应力值大于抗裂应力，桩基拉应力已不能满足抗裂要求，结构开裂。

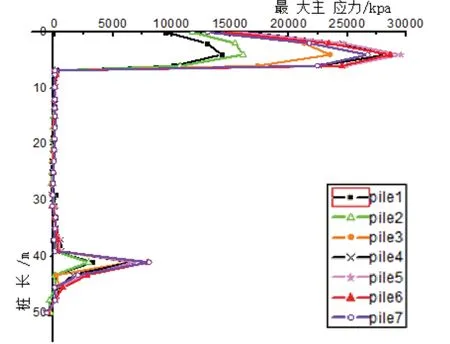
图8 泥面高程-3 m 时桩基最大主应力分布

3.6 桩基内力在不同回淤深度下的分布

码头总长1 500 m，共分4 个泊位，17 个结构分段。2015 年7 月对1#～4#泊位桩基检测发现，有114 根桩存在局部开裂。

通过分析，码头外部边界条件同原设计的最大区别在于码头水下岸坡淤积，而淤积体将对码头结构产生附加土压力荷载。因此有必要研究桩基内力的分布规律。桩基内力在不同回淤厚度下的分布如 表3 所示。

表3 不同回淤深度下内力计算

淤泥回淤对码头结构产生附加土压力荷载，且随着回淤深度的增大，桩基内力也逐渐增大。由表3 可见，直接影响的主要是pile1～pile5，并通过桩与桩之间的作用，进而传递到pile6、pile7，pile7的弯矩增加最明显，增大了4 倍，可见桩后淤泥回淤对于pile7 的受力最不利。

4 结 语

1）高桩码头桩后回淤对桩基内力影响显著，随着回淤深度的增大，高桩码头桩基最大拉应力和弯矩、轴力也逐渐增大。回淤深度为大于3 m 时，桩基拉应力已不能满足抗裂要求，导致部分结构开裂，且开裂部位在距离桩顶2 m 位置处。

2）高桩码头桩后回淤导致结构安全储备水平降低，耐久性下降，这类码头在运行过程中应定期对码头下部及后沿进行清淤，对桩基出现裂缝的应及时进行修复加固。