基于CQT的乐器独奏单旋律的提取

张 岩, 刘 哲

(沈阳师范大学 计算机与数学基础教学部, 沈阳 110034)

0 引 言

旋律通常指若干乐音经过艺术构思而形成的有组织、节奏的序列。国际音乐信息检索测评(music information retrieval evaluation eXchage,MIREX)将旋律定义为对应显著性人声或乐器中感知音高的基频值序列[1]。音乐学中,按照音乐作品旋律线的数量,将音乐分为单声部音乐和多声部音乐[2]。单声部音乐指同一时刻只有一个音符发音,如独唱、管乐器的独奏、演奏单旋律的弦乐器独奏等。单旋律提取是以单声部音乐为对象,对旋律的音高和时值等主要特征进行提取。单旋律提取可以应用于作曲创作、音准分析和校正、音乐检索和音乐情感分析等,因此具有重要的研究和应用价值。

1 乐音信号的旋律特征

1.1 乐音信号的频率

当发音体由于震荡而发出音时,每个音不仅仅包括基频正弦波的基音,还同时包括许多频率较高的正弦波的泛音[3]。复合波也是一种周期性的振动波[4],其振幅由基音的振幅和各组泛音的振幅重叠而成。根据十二平均律,计量上将一个八度音程即2倍频率之间分成12个音级,每2个相邻音级相差100音分(cent)。2个相邻音级的频率比是2(1/12)(约1.059 463)。2个相邻音分的频率比是2(1/1 200)(约1.000 577 79)。音列中乐音i的标准频率公式为F(i)=fa1·2(n/12),其中fa1=440为第一国际高度,n为乐音i到a1间隔的半音数目,当乐音i比音a1低时,n取负数[5]。

1.2 乐音信号的旋律特征分析

时频域分析是将时域与频域的处理方式结合起来,将信号分割成为时间帧,将时间帧内的信号进行时频变换,分析信号在时间域内的频谱特征[6]。短时傅里叶变换(short time Fourier transform, STFT)把整个时域过程分解成无数个等长的小片段,每个小片段近似平稳,再对时间窗的信号进行傅里叶变换(Fourier transform,FT)以获得具体在哪个时间点上出现了什么频率[7]。STFT的频率分辨率和时间分辨率是由加窗的窗口长度决定的,频率分辨率随窗长的加长而提高,时间分辨率随窗长的缩短而提高。频率分辨率就是在频率上将各次谐波分开的能力指标,时间分辨率就是在时间上将乐音分开的能力指标。显然,STFT窗口长度固定不变的变换方式造成了时间分辨率和频率分辨率的矛盾。为了解决这个矛盾,对音乐信号加窗后,采用常Q变换(constant Q transform, CQT)代替FT。

2 CQT算法

设有限长离散信号X(n),n=0,1,…,N-1,离散傅里叶变换(discrete Fourier transform, DFT)得到的X(k)的公式为

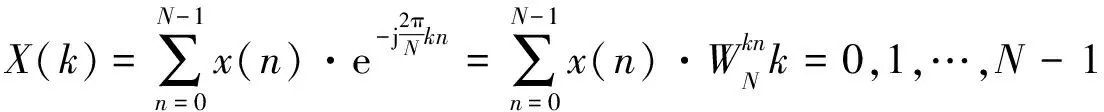
(1)

从离散傅里叶变换公式能够直观看出,X(k)是X(n)的一种近似表示,是单位频带的频谱值;任何周期信号都可以分解为直流分量、基频分量(k=0)和k次谐波分量。当然,实际中通常采用快速傅里叶变换(fast Fourier transform, FFT)来提高运行效率。

与傅里叶变换不同的是,CQT的中心频率是按指数规律分布的,并且中心频率与带宽比为常量Q。CQT频谱的横轴频率不是等间距的线性分布,而是计算log2的对数频率的不等间距分布。

若定义常量Q为中心频率与带宽的比值,则常量Q的计算公式为[8]

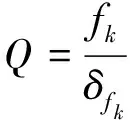
(2)

其中:fk是音乐信号在变换频谱内的第k个频率分量,称为中心频率;δfk是相邻半音的频率间隔,称为带宽,在信号处理时决定着频率分辨率(或频率解析度)。

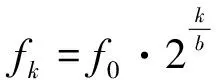
(3)

其中:f0是所处理的音频信号的最低频率;b是一个八度的频率范围内所包含的频谱线数[9]。一般情况下,b可以取值为12,24或36。若b=36,表示一个八度内有36条频谱线,即36个频率分量,每个半音有3条频率分量。

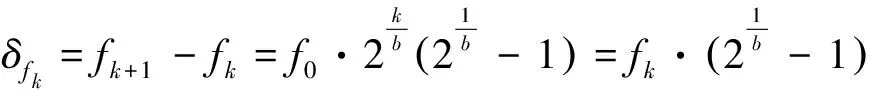
(4)

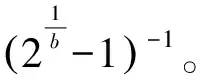
根据频率解析度的定义,可以得出窗长Nk,Nk的计算公式为

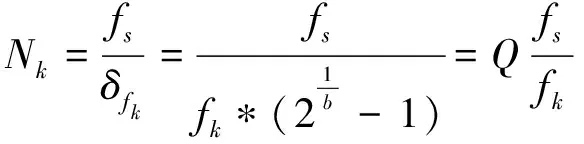
(5)

其中:fs是采样频率;fk是音乐信号在变换频谱内的第k个频率分量(中心频率)。

由于乐音信号的频率是按照指数规律分布的,所以CQT的频率分辨率能够与乐音的十二平均律相匹配,通过计算音乐信号的CQT谱,可以直接得到音乐信号在各个半音频率分量处的频谱值。根据以上计算过程,可以得出第k个频率分量的频谱值为

(6)

其中:x(n)是时域信号;wNk(n)是长度为Nk的窗函数,可以是矩形窗或汉明窗等;k是CQT谱的频率序号;Q是CQT的常数[11]。

由上面分析可知,CQT对于低频率的乐音信号可以获得良好的频率分辨率,而对于高频率的乐音信号可以获得良好的时间分辨率。对于低频分量,窗长较长;对于高频分量,窗长则较短。

3 基于CQT的单旋律提取算法

3.1 采用CQT算法提取单帧乐音信号的基频

在MATLAB中,可以使用fft函数实现快速傅里叶变换,从而求得该单个乐音的基频。这里以采样频率为44 100 Hz的单旋律小提琴曲为样本进行分析。通常情况下,小提琴A弦频率标准是440 Hz(对应钢琴的a1),G弦频率标准是196 Hz(对应钢琴的g),D弦频率标准是293.66 Hz(对应钢琴的d1),E弦频率标准是659.25 Hz(对应钢琴的e2)[12]。因为小提琴的频率范围为196～987.76 Hz,所以对低于175 Hz(约低于最低音2个半音)或者高于1 100 Hz(约高于最高音2个半音)范围内的噪声频率分量直接置零,以免造成窗长过长或过短的问题。

根据采样定理,FFT能分辨的最高频率为采样频率的一半(即Nyquist频率),函数fft返回值是以Nyqusit频率为轴对称的[13]。通过对fft函数求得的第一帧频谱的分析,前25个采样点就可以获得乐音的基频和主要谐波频率。依据前25个采样点,绘制如图1所示的茎状图。其中序号13的点是振幅最大值点,根据采样点频率的计算公式(n-1)·44 100/N(其中n表示采样点序号,n=1,…,N),计算基频的频率为(13-1)×44 100/1 024=516.8 Hz。

下面采用CQT算法分析乐音的基频。取b=12,Q=16.82,则第一帧的窗长Nk=Q·fs/fk=16.82×44 100/516.8=1 435.3,所以窗长可以取1 436个点。在MATLAB中,使用spectrogram函数对单乐音信号进行STFT分析。在spectrogram函数的参数中:window代表加窗函数,由主程序传递给spectrogram函数,这里采用Haming窗; nfft代表窗长的点数,也就是FFT的点数,一般为帧移的2倍,这里采用1 436;noverlap代表帧移,即重复点数,这里采用718;X代表音乐信号;fs代表乐音信号生成离散信号时的采用频率,这里从音乐数字文件的基本信息直接获取的是44 100 Hz。绘制的CQT时频图(也称语谱图)经过放大和中心移位后的效果如图2所示。

图2 CQT获得的乐曲第一帧信号的时频图Fig.2 Spectrum of first frame of music signal obtained by CQT

图2中能量最大的频率区域对应的就是基频所在区域,该乐音的基频范围是510～540 Hz;从spectrogram函数获得的S能量最大的F频率分量是522.08。因为440×1.059 4633=523.25,考虑到存在误差等情况,推断基音频率是523.25 Hz。从spectrogram函数也可以获得S能量最大的F频率分量所对应的时间点。因此,CQT算法能够获得更加准确的基频和时间点等特征,有利于乐曲的旋律特征的提取。

3.2 采用CQT算法提取乐曲旋律的算法及实现

算法的基本思想是将源信号的时间片段分帧,以帧为单位,转换成一个基于该时间帧的频谱图,然后依次将所有的分帧做相同的处理,就形成了时间轴上的时频图。时频图的横轴坐标为时间,纵轴坐标为频率,坐标值的明暗度为振幅值。具体算法流程如下:

1) 以1 024点为帧长,利用fft函数进行变换,获得基音频率fk。对超出正常乐音频率范围内的噪声,通过振幅置零的办法去除。

2) 利用CQT方法,在b=12,Q=16.82和已经获得的基音频率fk的条件下,计算第i帧加Hamming窗函数的窗长Nk(i)和重叠点数noverlap等。

3) 以计算得到的窗长和重叠点数为参数对信号重新动态分帧。

4) 利用spectrogram函数对每一帧进行STFT分析,获得能量最大值对应的基频和采样点序号等信息。第一帧的采样点序号为1,以后各帧的采样点序号TZ(i)=TZ(i-1)+Nk(i-1)/2。

5) 计算每帧的起始时间点,即时间点t=采样点起始序号/44 100[14]。

6) 根据基频和采样点起始序号或者基频和每帧的起始时间点,绘制乐曲的旋律阶梯图[15]。

选取整首小提琴曲的前100帧进行基频和采样点起始序号的提取, 提取结果如表1所示。对于各个帧提取的基频,可以根据情况和实际需要进行音准的修正。例如,第17,19和第26帧,频率为689.06,而689.06不是误差范围之内的乐音频率,判断存在噪声,可以取邻近值进行修正。

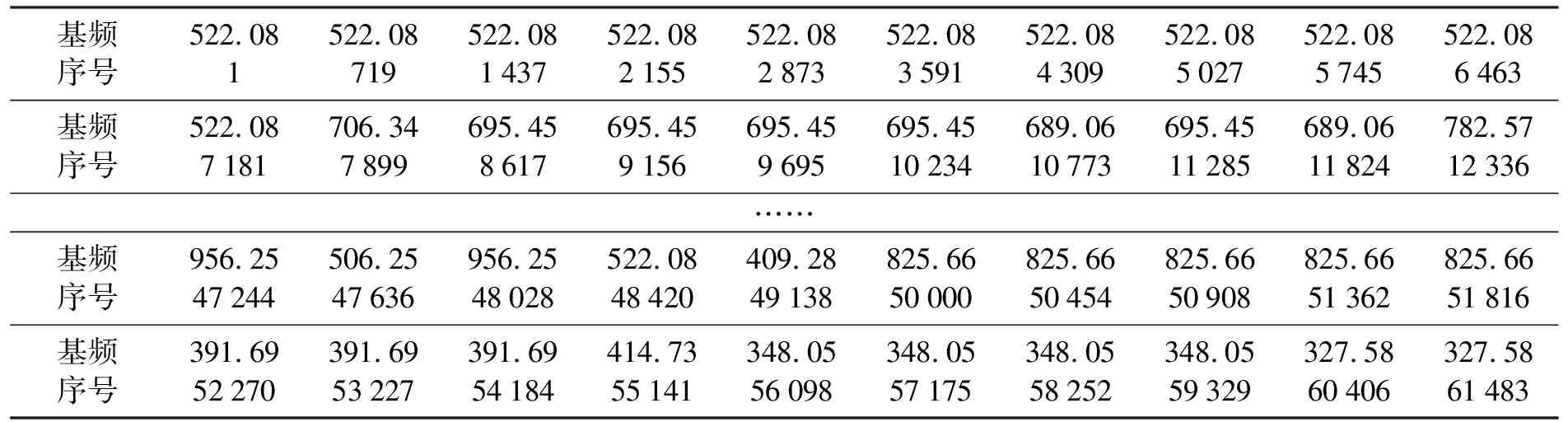
表1 单旋律小提琴曲前100帧的基频和采样点起始序号Table 1 f0 and starting sequence number of sampling point in the first 100 frames of single melody violin music

将基频和采样点起始序号换算为基频和起始时间点,在频率轴和时间轴上绘制的乐曲前100帧的旋律阶梯图如图3所示。

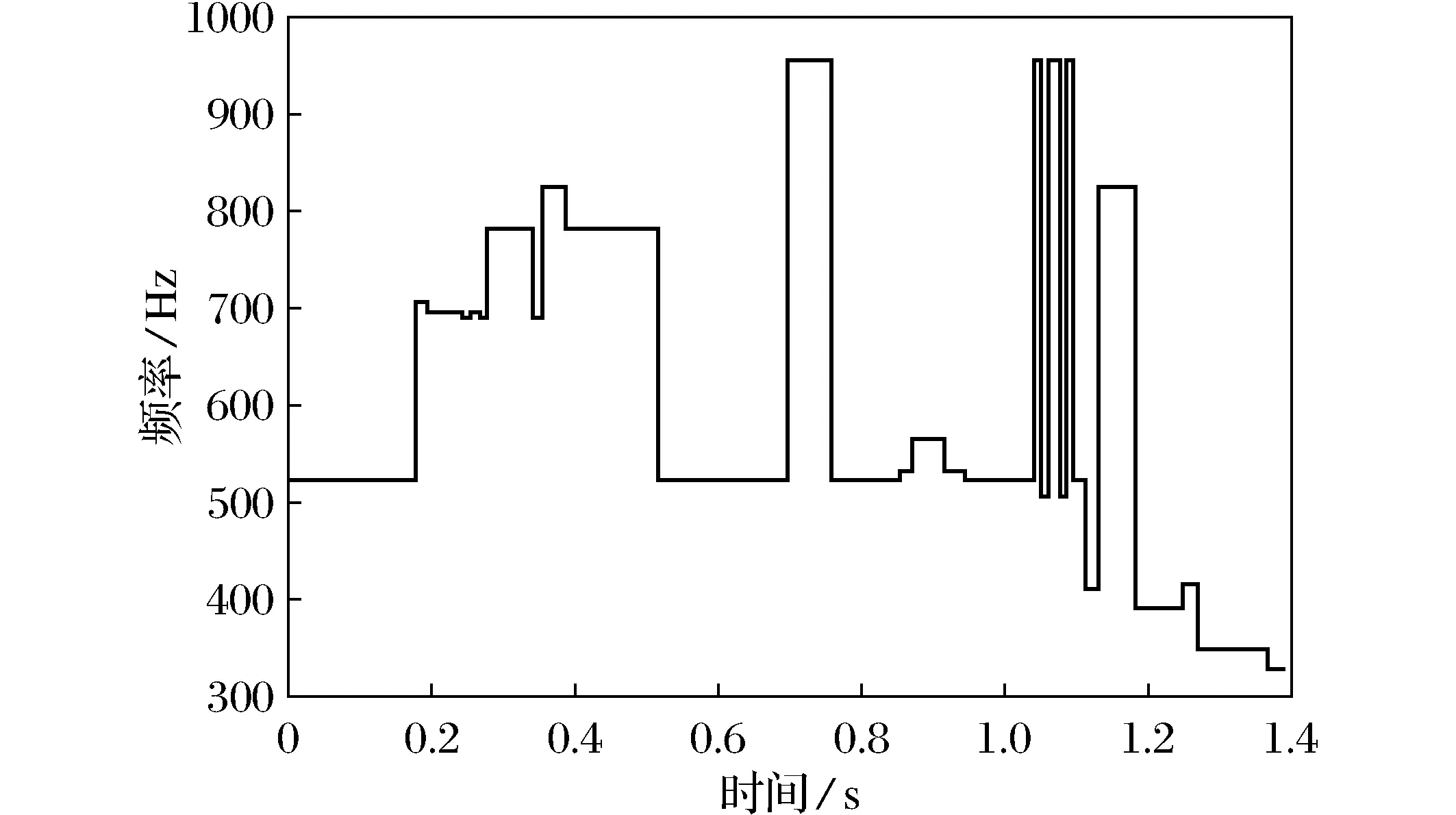
图3 乐曲前100帧的旋律阶梯图Fig.3 Melody ladder diagram of the first 100 frames of music signal

4 结 语

采用CQT算法,对于低频分量,窗长较长,截取的信号也较长,CQT变换后所获得频谱的频率分辨率较高;对于高频分量,窗长较短,截取的信号也较短,CQT变换后所获得频谱的时间分辨率较高[16]。以单旋律小提琴乐曲为样本,小提琴A弦频率440 Hz为标准,与钢琴相对应,小提琴的音域为小字组g～小字3组a3,在乐器本身的音准及采样时的误差范围内,可以基本检测出该乐曲的各帧基频,如表2所示。

表2 单旋律小提琴的部分基频检测值与标准值、钢琴琴键的对照Table 2 Comparison of partial f0 detection value of single melody violin with standard value and piano key

整首小提琴曲采样点总数为501 700 7个,取前100帧进行旋律提取,共抽取125 118个采样点(含重叠点)。与基于YIN算法的乐器单旋律提取结果相比较,从算法效率来看,增多了22 718个采样点,说明CQT动态变化窗长的算法可以明显地提高旋律提取的效率;从提取的基频与准确值的对照来看,检测值与准确值更加接近,说明CQT算法能更可靠地支持乐曲旋律的提取。当然,本方法提取的旋律存在需要改进的地方,主要是帧的采样起始点和音符的起始点之间存在误差的问题,对此需要进一步提取音符的起始点才可以实现对时间的准确定位。