Field-induced N´eel vector bi-reorientation of a ferrimagnetic insulator in the vicinity of compensation temperature∗

Peng Wang(王鹏), Hui Zhao(赵辉), Zhongzhi Luan(栾仲智),Siyu Xia(夏思宇), Tao Feng(丰韬), and Lifan Zhou(周礼繁),‡

1College of Mathematics and Physics,Qingdao University of Science and Technology,Qingdao 266061,China

2National Laboratory of Solid State Microstructures,Jiangsu Provincial Key Laboratory for Nanotechnology and Department of Physics,Nanjing University,Nanjing 210093,China

Keywords: spin Hall magnetoresistance,ferrimagnets,magnetic insulators,magnetization switching

1. Introduction

In ferrimagnetic materials,the magnetic moments in two or more magnetic sub-lattices with different magnetic moments are anti-ferromagnetically exchange-coupled, resulting in non-zero magnetic moments and angular momenta at absolute zero temperature. If the sub-lattice with a higher magnetic moment has a weaker molecular field than that of the sub-lattice with a lower magnetic moment, the total magnetization and angular momentum can be zero at certain temperatures, called the magnetization compensation point (TM)and the angular momentum compensation point(TA),respectively, owing to the different rates of decrease with temperature for diverse sub-lattices. Recently,the physical properties in the vicinity of TMand TAhave received increasing attention for their rich physics and potential high-speed and lowenergy-consumption spintronic applications.[1]For instance,the size of the skyrmions is reducible to the dimension of 10 nm in the vicinity of TMbecause of the significantly weak stray field.[2]The spin–orbit-torque efficiency substantially increases close to TMdue to the negative exchange interaction in ferrimagnets.[3,4]The domain wall motion mobility was found to be enhanced dramatically up to 2×104m·s−1·T−1close to TAin GdFeCo.[5]

In anti-ferromagnetic (AFM) spintronics, the control of the N´eel vector is of vital importance as it forms the basis for AFM information devices.[6]Two methods of manipulating the N´eel vector have been widely investigated: electric current and magnetic field(H). The N´eel-order manipulation by current was first reported in the conducting AFM CuMnAs via the staggered current-induced effective field.[7]Recent works have claimed the current-induced switching of the N´eel vector via the spin–orbit torque from an adjacent heavy metal layer,[8,9]but the validity of the experimental evidence is still under debate.[10]The N´eel vectors of anti-ferromagnets can be switched to perpendicular to H above a critical field,[11]known as the spin-flop(SF)transition. The AFM SF is widely used in the studies of spin transport in AFM insulators such as the spin Seebeck effect,[12]AFM magnon transport,[13]and spin superfluidity.[14,15]A field of the order of 10 T is usually required to achieve the SF phase.[16,17]The sub-lattice moments can be canted and then tuned to be aligned parallel to each other with a further increase in H. Ferrimagnets can be regarded as quasi-antiferromagnets in terms of nearly zero total moments in the vicinity of TM. In comparison with anti-ferromagnets, the compensated ferrimagnets show richer magnetic order transitions close to TMand their N´eel vector is easier to manipulate,[18–20]providing another platform for studying the rich physics related to the N´eel order.However,at present,it is generally believed that the N´eel vector of the compensated ferrimagnets undergoes an SF transition,and then all the sub-lattice moments turn toward H with a further increase in H.[18,19,21]

Most of the magnetic measurement techniques are not able to measure the N´eel vector of the compensated ferrimagnets because of the near-zero magnetization. The spin Hall magnetoresistance(SMR)[22,23]was previously demonstrated to act as a convenient tool for measuring the orientation of the N´eel vector of an AFM insulator.[24–26]In this study,we successfully used SMR to assess the magnetic order transition induced by the temperature(T)and H around TMof Gd3Fe5O12(GdIG).Notably,the SMR is negative sign for a certain range of H around TM. In contrast, the SMR is always positive for temperatures far from TM. We attributed this to the switching of the N´eel-vector direction of GdIG twice by H around TM, meaning that bi-orientation of the GdIG N´eel vector is achieved. The theoretical calculations combining the N´eel’s theory[27]and SMR theory[25,28]of ferrimagnetism are consistent with our observations and demonstrate the bi-reorientation of the N´eel vector.

2. Experimental details

Single-crystalline GdIG films were epitaxially grown on Gd3Ga5O12(111)(GGG)substrates by pulsed laser deposition(PLD)at 750◦C.The oxygen pressure during deposition was 9×10−3Torr(1 Torr=1.33322×102Pa)and the background vacuum was 2×10−7Torr. The energy of the laser pulse was 230 mJ/mm2. The surface morphology of the GdIG films was characterized by atomic force microscopy(AFM).The results are shown in Fig.1(a). The film is significantly smooth with a root-mean-square (RMS) roughness of 0.227 nm over a scanning area of 2µm×2µm. Figure 1(b)shows the x-ray diffraction (XRD) pattern of the GdIG/GGG film. A strong GdIG(444)peak was observed,indicating a good crystal quality. The magnetic properties of GdIG were characterized by a quantum design superconducting quantum interference device vibrating sample magnetometer (SQUID-VSM). The Pt Hall bars with 0.3-mm wide and 3-mm long were deposited on the GdIG films through a shadow mask by direct current(DC)magnetron sputtering at room temperature. The magnetoresistance (MR) measurements were performed in a physical property measurement system(PPMS)using the four-wire method with a combination of a Keithley 2400 SourceMeter and a Keithley 2002 voltmeter.

Fig.1. (a) AFM topography image of the GdIG/GGG (111) film. Root-mean-square roughness is 0.272 nm. (b) XRD pattern of our GdIG/GGG(111)film analyzed from 20◦to 90◦. (c)Temperature dependence of Ms for the GdIG(150 nm)/GGG(111)film. Red line is the fitting curve and the inset picture is a sketch of three different magnetic sub-lattices of GdIG.Double-headed arrows indicate exchange interactions. Inset figure shows the hysteresis loops of the GdIG(150 nm)/GGG(111)film measured at 70 K,190 K,and 280 K.

3. Results and discussion

The Fe3+ions in a unit cell of GdIG are surrounded by 8 oxygen octahedrons (a sites) and 12 oxygen tetrahedrons(d sites). The Gd3+ions sit in 12 oxygen dodecahedrons (c sites). The interaction between the a-site Fe3+ions and the d-site Fe3+ions is an anti-ferromagnetic super-exchange(exchange constant Jad) interaction, resulting in a net magnetic moment MFebecause of the unequal numbers of the a-site and d-site Fe3+ions. The Gd3+ions are ferromagnetically and anti-ferromagnetically coupled to the a-site Fe3+ions(exchange constant Jac)and the d-site Fe3+ions(exchange constant Jdc),respectively,[29,30]as schematically shown in the inset of Fig.1(c).The magnetic moment of the Gd3+ions MGdis anti-parallel to MFebecause of|Jac|≪|Jdc|.[31,32]Owing to the negligible interaction between the Gd3+ions and|Jdc|≪|Jad|,MGddeclines more rapidly than MFewith increasing temperature. Eventually,MGdand MFecancel out each other at TMto give the total magnetic moment of zero.[33]Figure 1(c) displays the T-dependence of the saturation magnetization Msof our GdIG (150 nm)/GGG (111) sample, where Msis extracted from the hysteresis loops. The hysteresis loops measured at three typical temperatures are shown in the inset of Fig.1(c).The coercivity is small,indicating a small anisotropy of GdIG.[34]It is observed that the behavior of Msis consistent with the above description and TMis ～185 K for this sample.This value is lower than the bulk value for GdIG ～288 K,[31]which may be due to the strain effect of the GGG substrate on the PLD grown film.[35]

In order to estimate the strength of the exchange interactions in the GdIG film,we fitted the curve of Msas a function of T [Fig.1(c)], with N´eel’s theory on ferrimagnetism. Because Jadis much larger than all other exchange constants,the a-site and d-site Fe sub-lattices are treated as a single entity with a net magnetic moment. Thus, GdIG can be simplified as a two-sub-lattice ferrimagnet including the Fe and Gd sublattices. According to the molecular field approximation, the T-dependence of Fe and Gd sub-lattice moments can be obtained by[36,37]

with

where gFe(Gd)=2 is the Land´e factor of Fe3+(Gd3+),[38,39]JFe=5/2 and JGd=7/2 are the angular momentum quantum numbers of the Fe3+and Gd3+ions, respectively; BJis the Brillouin function;µBis the Bohr magneton;µ0is the vacuum permeability; Nddis the intra-sub-lattice molecular field constant between the Fe3+ions;Ndcis the inter-sub-lattice molecular field constant; and kBis the Boltzmann constant. Here,the interaction between Gd3+ions is ignored. With the Curie temperature Tc～550 K[29]and H =0, we used the expression Ms=||MFe|−|MGd||and Eq.(1)to evaluate the goodness of fit. The equations fits very well with the data, as shown by the red line in Fig.1(c),with Ndd=68.6 T/µBand Ndc=4.4 T/µB,which correspond to the molecular fields of ～332 T between a-sites and d-sites Fe3+ions and ～21 T(for Gd)between Fe3+and Gd3+ions around TM,respectively.[36,40]The yielded TM=183 K is close to the experimental value. Such good agreement indicates that the molecular field approximation can accurately describe the evolution of the sub-lattice magnetic moments of the Fe3+and Gd3+ions as functions of T and H.

In normal metal/ferromagnetic insulator bilayers,the longitudinal resistivity (ρ) of the normal metal depends on the orientation of the magnetic moment,which is the SMR.[22,28]Considering ferrimagnetism with two magnetic sub-lattices,both sub-lattices contribute to the SMR. ρ is then given by[25,41]

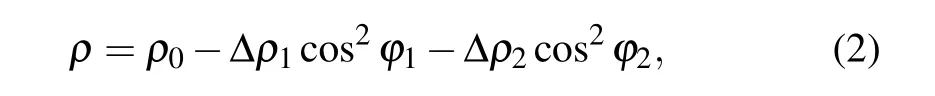
where ϕ1(ϕ2) is the angle between the magnetic moment M1(M2) of the sub-lattice and the spin polarization (σ) of the spin-Hall-generated spin current, ∆ρ1(∆ρ2) is the corresponding SMR coefficient of the magnetic sub-lattice, and ρ0is a constant resistivity offset. For an anti-ferromagnet or a ferromagnet close to TM, the N´eel vector is defined as n=(M1−M2)/|M1−M2|. When M1=−M2, one obtains ρ =ρ0−(∆ρ1+∆ρ2)cos2ϕn,where ϕnis the angle between n and σ, which is the same as the expression for the ferromagnet. Therefore,one can determine the direction of n using ρ.

The experimental geometry for the MR measurements is schematically shown in Fig.2(a). The directions of the DC and the normal direction to the sample are defined as the x and z directions,respectively. The resistivities of the 3-nm thick Pt strip on GdIG(150 nm)film were measured at 300 K by applying H along the x,y,and z axes,respectively. ρ significantly depends on the direction of H,and consequently the magnetization M, as shown in Fig.2(b). ρ increases with increasing H after M is saturated. This behavior was previously attributed to the Hanle MR[42]and the“new MR”.[43]More importantly,at high field,the expression ρ‖≈ρ⊥>ρTstill holds and the MR ratios ∆ρ‖/ρT= (ρ‖−ρT)/ρTand ∆ρ⊥/ρT=(ρ⊥−ρT)/ρT, remain positive, where ρ‖, ρTand ρ⊥are the resistivities for H ‖ x, H ‖ y, and H ‖ z, respectively.Angular-dependent MR (ADMR) measurements were then performed in a constant applied field while rotating the samples. The results forµ0H=1 T are shown in Fig.2(c),where∆ρ/ρ(angle)=[ρ(angle)−ρ(angle=90◦)]/ρ(angle=90◦),and the angles α,β,and γ are defined in Fig.2(a). ∆ρ/ρ(α)and ∆ρ/ρ(β) are positive for all angles. For the α-scan, the field is large enough to achieve H ‖M. ∆ρ/ρ(α) is well fitted with the cos2α function. For the β-scan, ∆ρ/ρ(β)deviates from the cos2β function owing to the misalignment of H and M caused by the demagnetization field.[44]The amplitude of the γ-scan is one order of magnitude smaller than those of the α-and β-scans.These features are similar to those of the Pt/Y3Fe5O12(YIG)system and are consistent with the SMR mechanism.[24,25]As ρ measured with H swept along the x and z axes and the ADMR for the α-and the β-scans are almost identical after M is saturated, we focused on the measurement of H applied along the x and y axes and the α-scan in the following studies.

Fig.2. (a)Schematic diagram of the MR measurements in three planes. Film plane is defined as the x–y plane. Current is applied along the x direction. α,β and γ are the angles between H and x(in x–y plane),z(in y–z plane),and z(in x–z plane)axes, respectively. (b)Resistivity as a function of field measured on the Pt (3 nm)/GdIG (150 nm)/GGG (111) sample for field applied along x, y, and z axes. (c)ADMRs measured in the x–y, y–z, and x–z planes withµ0H=1 T.All measurements are performed at 300 K.

Fig.3. (a) ADMRs measured in the x–y plane for the Pt (3 nm)/GdIG(150 nm)/GGG(111)sample at three different temperatures withµ0H=1 T.(b) Temperature-dependence of the SMR ratios extracted from the ADMRs measured in the x–y plane withµ0H=1 T.

Figure 3(a) shows the ADMR results of the α-scans atµ0H = 1 T and three typical temperatures (100 K, 190 K,and 280 K). At T =280 K and 100 K, which are far from TM, ∆ρ/ρ(α) is always positive, meaning that ρ‖>ρT. At T = 190 K, in the vicinity of TM, the curve is shifted by 90◦as compared to the data measured at T = 280 K and 100 K, leading to ρ‖＜ρTor a negative SMR. The ADMR at 190 K exhibits a slight deviation from the cos2α function because of the misalignment of H and M in the vicinity of TM. The ADMR around TMcould produce complex angular dependence since sub-lattice magnetic moments have different angular dependence on magnetic field for an inhomogeneous sample.[20]We carried out the same measurements from T =300 K to T =100 K.The extracted SMR ratio is shown in Fig.3(b). The SMR is negative close to TMof GdIG. In comparison, for the ferrimagnetic insulator YIG, which has no magnetization compensation point,the SMR for Pt/YIG is positive,[46,47]suggesting that our observation is related to the magnetic structure transition for GdIG close to TM.

A simple method to directly assess the magnetic structure transition is through magnetic moment measurement techniques such as SQUID-VSM. For our GdIG (150 nm)/GGG(0.5 mm)sample,the magnetic moment of the GGG substrate is approximately two and three orders of magnitude higher than that of the GdIG film at 300 K and 190 K, respectively,for µ0H =1 T. Therefore, this approach is not suitable because the paramagnetic signal of the GGG substrate is too large to accurately determine the magnetic structure transition of GdIG. Instead, we performed MR measurements as a function of H to investigate the negative MR close to TM.This method has been verified to be a reliable tool in determining the orientation of the N´eel vector of an anti-ferromagnetic insulator.[24–26]Figure 4(a)shows ρ‖and ρTas a function of H for H applied along the x and y axes,respectively,at 190 K.The sharp downward peak of ρ‖near H = 0 is due to the magnetization reversal at the coercivity of GdIG, similar to the peaks in Fig.2(b). After H exceeds the saturation field(～0.1 T), M should be aligned with H. In this range of magnetic field,the SMR predicts the constant ρ‖and ρT,and the“new MR”mechanism predicts the monotonic increases in ρ‖and ρT. However, our observations are inconsistent with these two predictions. ρ‖and ρTnotably demonstrate nonmonotonic behaviors with minimum and maximum values,respectively, as shown in Fig.4(a). As a result, ∆ρ‖/ρTis positive in low magnetic fields, negative in the field range of～0.40 T＜µ0H ＜～1.65 T with a maximum negative SMR ratio of approximately −3.2×10−4at ～0.8 T,and then turns positive atµ0H>～1.65 T,as shown in Fig.4(b).

Fig.4. (a) Resistivity as a function of H with H applied along the x and y axes at 190 K.(b)Calculated ∆ρ‖/ρT from 0.1 T to 9 T using the data from(a).

These findings are only observed when T is close to TMstrongly suggesting that this phenomenon is connected with the compensated ferrimagnetism. A negative SMR was observed in Pt/NiO/YIG tri-layers due to a critical temperature where the SMR changed from positive to negative with decreasing T.[26,48–50]The negative SMR is attributed to either the occurrence of spin-flip scattering for the reflected spin at the NiO/YIG interface or the spin being reflected back at the Pt/NiO interface and the SF coupling between YIG and NiO. Whichever conclusion is correct, neither can be applied to our system because of the absence of the antiferromagnet/ferromagnet interface for the spin-flipping scattering or SF coupling in a single GdIG layer. A negative SMR was also reported in the heterostructure of a heavy metal Pt and an anti-ferromagnet,[24]which is explained by the 90◦phase-shift due to the H-induced SF.However,the SMR does not change sign in presence of sweeping H,implying that the explanation of a negative SMR cannot be applied to our system. In fact, a negative SMR was previously observed in Pt and indium/yttrium-doped GdIG(Y1Gd2Fe4In1O12)bi-layers close to the TM, which is attributed to the negligible contribution of Gd to the SMR and MFeperpendicular to H at a relatively large H close to TM.[41]The second change in the sign of SMR can occur when H exceeds the AFM coupling strength (～21 T for our sample according to the fitting results with Eq.(1))to align MGdand MFeto a parallel position.[36,41]However, this is inconsistent with our observation that the second change in the sign of SMR occurs atµ0H ＜2 T. Therefore, the conclusion that the second SMR sign change is due to the alignment of MGdand MFeis invalidated.

Here,we proposed a model within the molecular field approximation framework that fits our observations. The energy E in GdIG due to the Zeeman energy of the molecular fields and the external field is given by

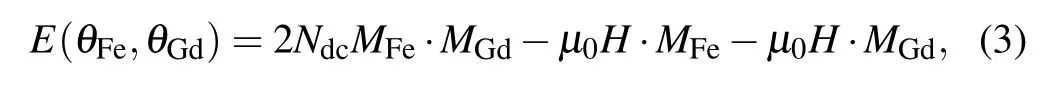
where θFe(Gd)is the angle between MFe(Gd)and H,as defined in the inset of Fig.5(a). Because of the small anisotropy of the(111)-oriented GdIG,[34]the magneto-crystalline anisotropy energy is ignored. Combining Eqs. (1) and (3), the Hdependences of θFeand θGdcan be calculated numerically by computing the minimum value of E(θFe, θGd). The result at T = 190 K is shown in Fig.5(a). At low magnetic fields,the normalized N´eel vector nGdIG=(MFe−MGd)/|MFe−MGd|is parallel to H due to the small net magnetic moment.At µ0H ≈0.9 T, an SF transition, that is nGdIG⊥H, occurs.However, with a further increase in the magnetic field, unlike antiferromagnets in which both sub-lattice moments tilt towards H,MFe,and MGdtend to align antiparallel and parallel with H,respectively,and nGdIGaligns anti-parallel with H. The bi-reorientation transition of the N´eel vector is shown in Fig.5(b). With θFe(H)and the SMR mainly contributed by the Fe sub-lattice moments suggested by Ref.[41],ρ is calculated from Eq.(2)as

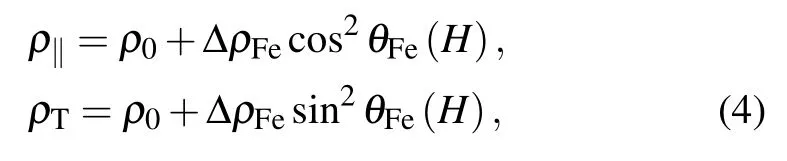
where ∆ρFeis the SMR coefficient for the Fe sub-lattice. The calculated results of Eq. (4), as shown in Fig.5(c), are in good agreement with the experimental results [as shown in Fig.4(a)]. Based on the good agreement between the theoretical and the experimental results,we concluded that the observed SMR behaviors originate from the field-induced N´eelvector bi-reorientation.

Fig.5. (a)Calculated results of θFe (brown line)and θGd (green line)using Eqs. (1) and (3) at 190 K and the inset defines θFe and θGd. (b) Orientations of the Fe sub-lattice and Gd sub-lattice moments with respect to the H where H =H1, H2, and H3, which are defined in (a), n is the N´eel vector of GdIG.(c)Calculated resistivity as a function of field using Eq.(4)and the data shown in(a).

In addition to theoretical calculations, this observation can be understood phenomenologically. Because of the very strong interaction between the Fe3+ions and the weak interaction between the Gd3+ions, the Fe and Gd sub-lattices in GdIG can be considered individually as a“ferromagnetic system” and a “paramagnetic system”, respectively. MGdis induced by the external and molecular fields. At T ～TM, that is, MFe≈−MGd, GdIG undergoes an SF transition or a reorientation of nGdIGfor a relatively large magnetic field similar to an anti-ferromagnet. On further increasing the magnetic field, MFeremains constant as a “ferromagnet”. In contrast,MGdincreases significantly as a“paramagnet”when the magnetic field is increased leading to |MFe|＜|MGd| or the transformation from an anti-ferromagnet into a ferrimagnet. As a result, MFeor nGdIGis aligned antiparallel with H above a critical magnetic field, indicating the occurrence of a second re-orientation[Fig.5(b)]. Our findings indicate that the direction of the N´eel vector of a ferrimagnet can be tuned across a wide range from 0◦to 90◦and then to 180◦by the appropriate external magnetic field close to the TM.

4. Conclusions

We systematically investigated SMR in Pt/GdIG bilayers under a wide range of temperatures and magnetic fields. Our findings indicate that SMR in Pt/GdIG bilayers is positive for temperatures far from TM, similar to that of the Pt/YIG bilayer. In the vicinity of TM,the field-dependent SMR ratio not only exhibits a non-monotonic behavior, but also changes its sign twice.We attribute this behavior to the field-induced N´eel vector bi-reorientation. This observation can be explained by the fact that the Gd sub-lattice moment increases more rapidly than the Fe sub-lattice moment by the external field since the molecular field of the Gd ions are much weaker than that of the Fe ions. We also showed that the calculations based on the molecular field approximation and SMR theory can accurately predict the experimental phenomena. Our results demonstrate that SMR is a simple method for detecting accurately the N´eel vector of a ferrimagnet. The direction of the N´eel vector of a ferrimagnet can be tuned across a wide range by an external magnetic field in the vicinity of TM.