Quantifying entanglement in terms of an operational way∗

Deng-Hui Yu(于登辉) and Chang-Shui Yu(于长水),2,†

1School of Physics,Dalian University of Technology,Dalian 116024,China

2DUT-BSU Joint Institute,Dalian University of Technology,Dalian 116024,China

Keywords: quantum entanglement,entanglement measure,quantum resource theory

1. Introduction

Entanglement is one of the most intriguing quantum features[1,2]and plays an important role in many quantum information processing tasks,[3,4]so quantum entanglement has been recognized as a key physical resource in quantum information.[5–12]Quantification of entanglement, triggering the various researches on the quantum resource theory,[13–28]has attracted wide interest for several decades. However,quite limited progress has been made up to date,due to the good understanding of entanglement only restricted to bipartite pure states and low-dimensional mixed states.[29–37]

The quantification of any quantum resource actually aims to quantitatively characterize the corresponding quantum feature in a mathematically rigorous framework.[13]As to entanglement, a good quantifier should be an entanglement monotone which vanishes for separable states and does not increase under local operations and classical communications (LOCC).[36]There are various such entanglement monotones, however, only a few of them have the obvious operational meanings. For example, distillable entanglement quantifies the conversion rate of some standard state (maximally entangled state) from the given states in the asymptotic regime, while entanglement cost quantifies the rate of the expected state asymptotically prepared from some standard state.[36,38,39]In spite of the relative entropy of entanglement[40]defined by the nearest distance from a given state to the set of separable states based on the “distance”, the relative entropy could have an operational meaning, whereas most of the distance-based measure has only the geometric meaning. The convex roof construction[41,42]is a useful approach to establish an entanglement monotone,which generally has no explicit operational meaning, while the entanglement of formation[36]can be closely related to the entanglement cost in the asymptotic regime.[39]Similarly,the negativity has not a striking operational meaning,[43]but the logarithmic negativity provides an upper bound to distillable entanglement.[44]Different ways to quantifying entanglement usually convey different understandings of entanglement, in particular, their potential operational meanings are usually connected with different quantum information processing tasks. How to explore an operational approach to quantify entanglement is still an important and significant topic in the entanglement theory.

In this paper,we propose an operational way to build entanglement monotones similar to our previous approach for coherence.[23]We consider that some pure input states are converted to the common objective quantum state by LOCC. It is shown that the entanglement of the objective quantum state can be well characterized by the least entanglement of the pure input states. We prove that any given pure-state entanglement monotone F can induce a good entanglement monotone for a general quantum state,and especially that our entanglement monotone is the largest one among all the entanglement monotones that take the same value for pure states as F. We also show that our entanglement monotone will be equivalent to the entanglement monotone in terms of the convex roof construction if the convexity is imposed. As was demonstrated,we show that if the chosen pure-state entanglement monotone linearly depends on the Schmidt coefficients or we use the two-qubit concurrence as pure-state measure, our entanglement monotone will be equal to that of the convex roof construction. In addition, an analytically computable example indicates that our approach induces an entirely new entanglement monotone. This paper is organized as follows. In Section 2,we directly build the entanglement monotone based on the state conversion, and then show that our entanglement monotone is the maximal one. In Section 3, we study how our method is related to the convex roof construction. In Section 4,we demonstrate several examples in various cases. The conclusion and discussion is given in Section 5.

2. Entanglement monotone based on the state conversion

Let us consider a bipartite quantum state ρ =∑ipi|ψi〉〈ψi| with an alternative pure-state realization{pi,|ψi〉}. We take λ↓(|ψi〉) to denote the Schmidt vector of the state |ψi〉 with the Schmidt coefficients in decreasing order. It was shown in Ref. [45] that if there exists a bipartite pure state |ϕ〉 with λ↓(|ϕ〉)≺∑ipiλ↓(|ψi〉), where ≺is the majorization,[46–48]one can always find an LOCC to transform the state|ϕ〉to the state ρ. It is obvious that for a fixed density matrix ρ, the state |ϕ〉 is not unique. In fact, with the entanglement taken in account,one can also notice that all these pure states|ϕ〉do not necessarily have the equal amount of entanglement. Let L(ρ)denote the set of pure states which can be transformed into ρ by LOCC and F(···)denotes an arbitrary entanglement monotone of pure states, we are always able to define an entanglement quantifier for ρ by the smallest amount of entanglement of the pure states in L(ρ),which can be given in the following rigorous way.

Theorem 1For any bipartite quantum state ρ, let L(ρ)be the set of pure states which can be transformed into ρ by LOCC,then

is an entanglement monotone, where the subscript F denotes the chosen entanglement monotone F(···)of pure states.

Proof(Vanishing for separable states)Firstly,we would like to show that if a state ρ is separable, there must exist a separable pure state in the set L(ρ). To show this, one can note that any separable state ρ can be expressed as a convex combination of some pure product states {pi,|φi〉}, so∑ipiλ↓(|φi〉)=(1,0,0,...)which majorizes the Schmidt vector λ↓(·) of any pure product state |φ〉. From Ref. [45], it is easily found that ρ can be converted from a pure product state|φ〉by LOCC,which shows F(ρ)=0.

Conversely,if F(ρ)=0,the definition implies that there exists pure product state that can be transformed into ρ by LOCC,thus ρ is separable.

(Monotonicity)Suppose that ε is an arbitrary LOCC and σ = ε(ρ). Let |ψ〉 be the optimal state in L(ρ) such that EF(ρ)=F(|ψ〉). Based on the definition of EF(ρ), we have|ψ〉 that can be converted into ρ by LOCC. In addition, σ =ε(ρ), one can find that |ψ〉 can also be converted into σ by LOCC, i.e., |ψ〉 ∈L(σ), which implies EF(ρ) = F(|ψ〉) ≥EF(σ).

(Strong monotonicity) Suppose that |ψ〉 is the optimal state in L(ρ) such that EF(ρ)=F(|ψ〉). It means that there exists a decomposition{ti,|ϕi〉}of ρ with

That is,|ψ〉can be converted to{ti,|ϕi〉}.Let an LOCC$with its Kraus operators{Mk}performed on the state ρ with

Substituting the decomposition{ti,|ϕi〉}into Eq.(2),one will obtain

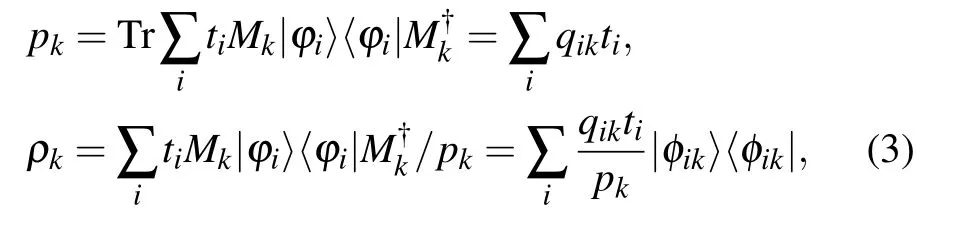
with

where|ψk〉is defined as a pure state satisfying

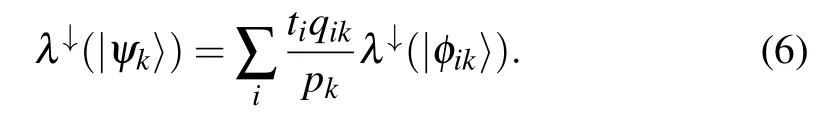
Equation (5) indicates that |ψ〉 could be transformed into{pk,|ψk〉} by LOCC, so the entanglement monotone F(···)gives

In addition,Eqs.(3)and(6)show|ψk〉∈L(ρk),thus

Therefore,

which is the strong monotonicity.

One can find that the set L(ρ) is actually defined by the state |ψ〉 subject to the majorization relation λ↓(|ψ〉)≺∑ipiλ↓(|ψi〉) with {pi,|ψi〉} denoting the decomposition of the state ρ. However, from the above proofs, an important relation is

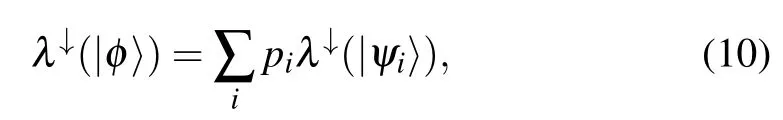
where|φ〉is a pure state.It is obvious that λ↓(|ψ〉)≺λ↓(|φ〉),which implies F(|φ〉)≤F(|ψ〉). Thus the set L(ρ)in Eq.(1)can be replaced by its subset Q(ρ)⊂L(ρ),where Q(ρ)covers all the pure states|φ〉satisfying Eq.(10).

Theorem 1 has provided us with an operational way to define an entanglement monotone from a pure-state entanglement monotone F. That is, the entanglement of a state ρ quantifies the least entanglement of the pure states which can be converted into ρ. It is obvious that different F will induce different EF. In fact,there are many different entanglement monotones which can be reduced to a fixed entanglement monotone for pure states, which, to some extent, forms the root of a fundamental requirement of a general entanglement measure: all entanglement measures should be reduced to the von Neumann entropy of entanglement for pure states. Next we will show that our proposed entanglement monotone EFis the upper bound of all the entanglement monotones which are identical to F for pure states.

Theorem 2Given an entanglement monotone E(ρ) for any bipartite density matrix ρ such that E(|ψ〉) = EF(|ψ〉)holds for any bipartite pure state|ψ〉,then EF(ρ)≥E(ρ).

ProofSuppose that|ψ0〉is the optimal state in L(ρ)such that EF(ρ)=F(|ψ0〉),then we have

the last inequality is due to the monotonicity of E.

3. Relation with the convex roof construction

We have shown that EFis a valid entanglement monotone, so it can be safely used to quantify entanglement of a state. However, some additional properties are also imposed sometimes. One example of the properties is the concept of convexity. Next we will give the sufficient and necessary condition for a convex EF.

Theorem 3For bipartite n-dimensional quantum states,the following statements are equivalent to each other:

(I)EF(ρ)is convex.

(II)EF(ρ)is equivalent to the convex roof construction in terms of F(·).

(III) For any ρ, the optimal pure state |φ0〉∈Q(ρ) and the related decomposition {qk,|ϕk〉} satisfy: (1) F(|φ0〉) =∑kqkF(|ϕk〉), (2) {qk,|ϕk〉} is the optimal decomposition of ρ for the convex roof construction.

(IV)F satisfies: (1)F(···)should be a linear function of the decreasing order Schmidt coefficients of a pure state,or(2)for all n-dimensional states ρ,there should be an optimal purestate decomposition for the convex roof construction with all the pure states owing the same Schmidt coefficients.

ProofLet|φ0〉∈Q(ρ)be the optimal pure state for EF,then there exists a decomposition{qk,|ϕk〉}corresponding to|φ0〉such that Eq.(10)holds. If EFis convex,we will arrive at

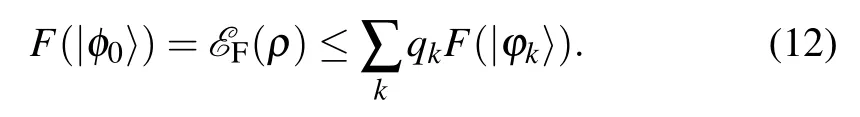
A general entanglement monotone F(···)for a bipartite pure state can always be expressed as a concave function f of the Schmidt coefficients of the pure state, namely, f(λ(···))=F(···).[42]From the concavity, we have f(λ(|φ0〉)) ≥∑kqkf(λ(|ϕk〉)), namely, F(|φ0〉)≥∑kqkF(|ϕk〉). Thus for the optimal state |φ0〉 and its corresponding decomposition{qk,|ϕk〉}of ρ,we have

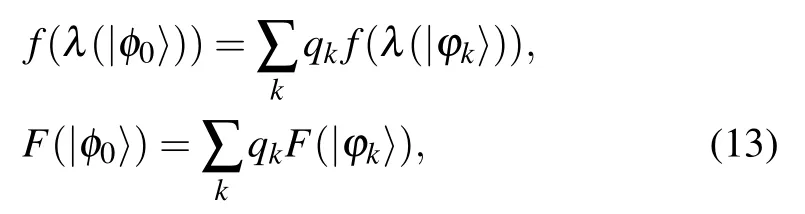
which implies the decomposition {qk,|ϕk〉} achieving min{pi,|ψi〉}∑ipiF(|ψi〉) and EFequal to the minimum. Thus one can arrive at (II) and (III) from (I). Since Eq. (13) should be satisfied for any n-dimensional density matrix ρ, one can easily find that (1) F(···) should be a linear function of the Schmidt coefficients of a pure state, or (2) for all ndimensional states ρ, there should be an optimal pure-state decomposition for the convex roof construction with all the pure states owing the same Schmidt coefficients. Thus we can reach(IV)from(I).

Conversely, if (II) or (III) holds, (I) will clearly hold. If(IV)(1)holds,then f(λ(|φ〉))=∑ipif(λ(|ψi〉))and F(|φ〉)=∑ipiF(|ψi〉) will hold for all |φ〉∈Q(ρ) and the related decomposition {pi,|ψi〉}. Note that F(|φ0〉) reaches the minimum in Q(ρ), thus the decomposition {qk,|ϕk〉} related to|φ0〉achieves the minimum of the convex roof.Thus EFequals the convex roof and inherits the convexity. If (IV) (2) holds,suppose that the particular decomposition is{˜pj,|˜ψi〉},|˜φ〉denotes the state in Q(ρ)related to it,then

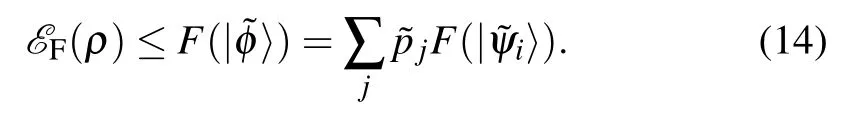
Note that the above summation equals the convex roof. Combining with Theorem 2,one can see that EFequals the convex roof and inherits the convexity. The proof is completed.

Theorem 3 shows that the convex EF(ρ) is equivalent to the convext roof construction. One should note that if theorem 3 is valid for all n,EF(ρ)will be the same as the convex roof construction in the whole state space. In addition,one important thing is that if the convexity is not imposed,EFwill be a new entanglement monotone. In the next section,we will give examples subject to different cases.

4. Examples

The same as convex roof with the linear F(···). As the first example, we will demonstrate that EFis the convex roof of F with a proper F.To do so,we choose the distillable entanglement monotone〈E〉for pure states proposed in Ref.[45]as our entanglement monotone F. For a d-dimensional pure state|ϕ〉,the entanglement monotone is defined by

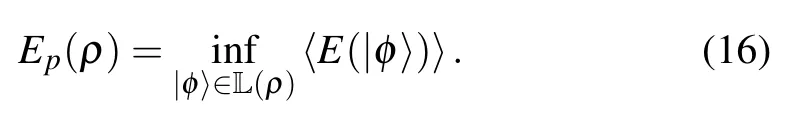
Based on the definition of 〈E〉 in Eq. (16), one can find that〈E〉linearly depends on the Schmidt coefficients λn,which means that Theorem 3 is satisfied.Thus,our established entanglement monotone Ep(ρ)is equivalent to the convex roof construction in terms of the pure-state entanglement monotone〈E(|ϕ〉)〉.

The same as convex roof for two-qubit concurrence.It has been shown in Ref.[33]that there always exists such an optimal pure-state decomposition of a bipartite density matrix of qubits that all the pure states have the same concurrence,[49]i.e., the Schmidt coefficients for two-qubit states. Thus, one can easily find that our EFfor qubit states is equal to the convex roof of concurrence based on our Theorem 3. In other words,if we select F as concurrence,EFwill be convex in the(2⊗2)-dimensional Hilbert space.

A new entanglement monotone. The decomposition similar to bipartite qubit states does not always exist for a highdimensional system in general cases, thus one can find that EFwill provide a new entanglement monotone. To give an explicit demonstration,we consider the following analytically computable example,by which one will find that EFis different from the convex roof construction.

Theorem 4For a (3 ⊗3)-dimensional bipartite density matrix

where |ϕ0〉=c1|11〉+c2|22〉, and |k〉 denotes the computational basis,

with |θ〉 denoting the pure state with the Schmidt vector λ↓(|θ〉)=ηλ↓(|ϕ0〉)+(1 −η)λ↓(|33〉), and F is an entanglement monotone for pure states.

ProofConsider any decomposition {pi,|ψi〉} of σ with σ =∑ipi|ψi〉〈ψi|,the Hughston–Jozsa–Wootters(HJW)theorem[29,50]implies that|ψi〉can always be written as

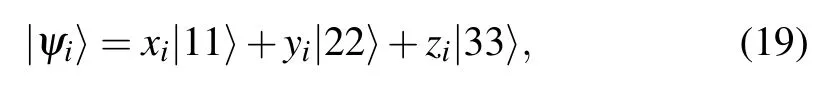
where xi,yi,ziare the amplitudes with|xi|2+|yi|2+|zi|2=1.Since σ = ∑ipi|ψi〉〈ψi|, the corresponding elements of the right- and left-hand sides with respect to the basis {|kk〉}should be consistent with each other,which means

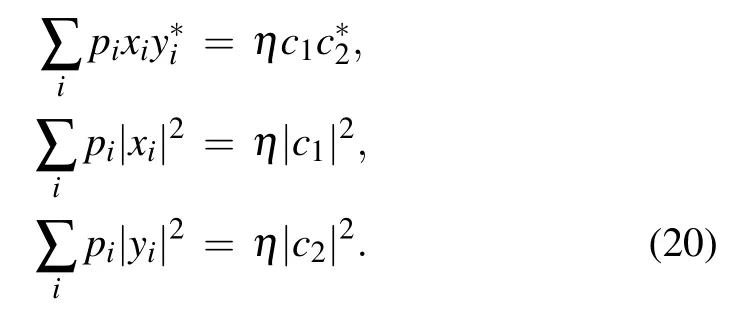
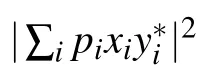
where |θ〉 is a state with the Schmidt vector λ↓(|θ〉) =ηλ↓(|ϕ0〉)+(1 −η)λ↓(|3〉|3〉). Note that λ↓(|θ〉) has only two non-zero elements,thus Eq.(21)implies

That is, any pure state |φ〉 in Q(σ) (with ∑ipiλ↓(|ψi〉) =λ↓(|φ〉)) satisfies λ↓(|φ〉)≺λ↓(|θ〉). Therefore, the monotonicity of F shows F(|φ〉)≥F(|θ〉),which means that|θ〉is the optimal pure state in Q(σ),i.e.,EF(σ)=F(|θ〉).

Based on Theorem 3,our entanglement monotone equivalent to the convex roof construction requires the condition(III).For the state σ,we have EF(σ)=F(|θ〉). However,the optimal pure state|θ〉should correspond to the optimal decomposition with the average entanglement given by ηF(|ϕ0〉). It is obvious that ηF(|ϕ0〉)=F(|θ〉)does not hold for general parameters and F(···). Therefore,one can draw the conclusion that our approach induces a new entanglement monotone.

5. Discussion and conclusion

In summary,we have provided an operational way to define an entanglement monotone. Since all the bipartite pure states can be converted into their corresponding mixed/pure objective states by LOCC, we define the entanglement of the objective state by the least entanglement of the pure state which can be converted into the objective state of interest. We prove that any entanglement monotone of pure states can induce an entanglement monotone of a general quantum state in terms of our approach. In particular,we prove that our entanglement monotone is the maximal one among all those having the same values for pure states as ours. In addition, we show that if the convexity is considered,our approach will be equivalent to the convex roof construction. Thus our approach can provide the operational meaning for the entanglement monotone based on the convex roof construction. Finally,we would like to emphasize that our approach could also be feasible for the quantification of other quantum resources. This work could motivate the relevant research on the state conversion by free operations.