一种基于小波的相关系数判别变压器励磁涌流的方法

陈映芳，姚 琳

(1.广州铁路职业技术学院电气工程学院，广东 广州 510430；2.上海第二工业大学能源与材料学院，上海 201209)

差动保护作为变压器的主保护，其保护动作的快速性和可靠性受到整个行业的普遍认可。然而基于差动保护原理的主要缺陷在于变压器通电时产生的瞬态励磁涌流而造成误动作[1]。为防止励磁涌流造成的误动作，通常是采用谐波制动比的方法，其主要原理是利用励磁涌流的二次谐波(或五次谐波)分量比基波电流分量大来判断是发生内部故障还是励磁涌流。如果差动电流的二次谐波含量超过了预定基波分量的百分比，就判定有励磁涌流情况的发生，从而闭锁差动保护，使保护不会误跳闸。这些技术的主要缺点之一是继电器动作速度慢[2]。

然而，变压器内部故障时也可能产生二次谐波分量，这是由于电流互感器饱和或与变压器相连的电容器暂态过程造成。如并联电容器或超高压(特高压)长传输线中分布电容等[3-4]。对于变压器差动保护的励磁涌流的判别算法主要包括人工神经网络、磁通和电压约束以及模糊逻辑算法等[3]。但是，这些方法对变压器的参数依赖性强，随着变压器运行时间的增加，其判别效果很容易受到影响[5]。此外，这些方法需要复杂的算法来进行计算。

小波分析和小波变换是近年来出现的一种强大的信号处理工具。在电力系统的应用中，利用小波的瞬态特性可以对具有复杂时频结构的信号进行准确有效的分析[6]。

因此，本文提出一种基于离散小波变换和相关系数的简单方法来区分内部故障和励磁涌流。具体的技术路线是，将算法分为离线状态和在线状态两部分。离线状态时，对前半周差动电流第5 级细节系数的能量之和进行计算；在线状态时，用小波变换db1 函数对其进行分解，并与历史存储的典型励磁涌流指标和记录信号的相关系数比较，判别励磁涌流和内部故障。最后，本文利用励磁涌流和内部故障电流数据进行仿真实验，测试该方法的有效性。

1 离散小波变换

小波变换将信号表示为不同位置和尺度(持续时间)的小波和。小波系数作为小波变换的权值来表示这些位置和尺度上的信号。目前，离散小波变换(Discrete Wavelet Transform，DWT)在非周期的暂态信号分析中非常有效，已经被广泛应用。

离散小波变换通过正交镜滤波器(Orthogonal Mirror Filter，OMF)对输出信号进行两倍采样率的反采样，同时将低通滤波器的输出信号送入另一个相同的正交镜滤波器对。这种信号处理的操作像数或金字塔算法递归地重复，产生一组信号，这些信号将原始信号的频谱划分为8 个频带，随着每个频带宽度的缩小和频率的降低，在时间上依次进行更粗略的测量[7]。图1 为多分辨率离散小波变换树算法示意图。

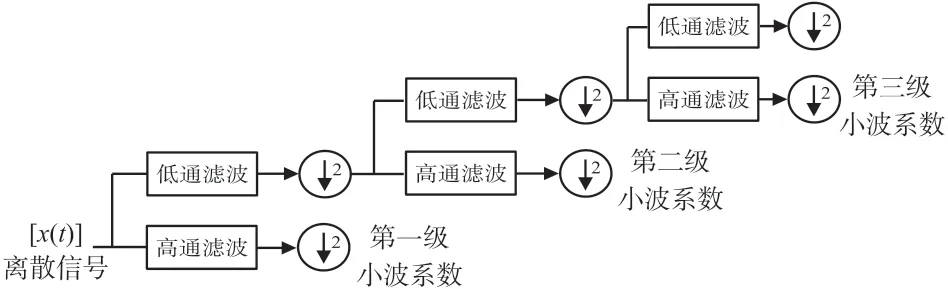
图1 离散小波变换多分辨率算法示意图

在小波分析中经常用到近似与细节，近似表示信号的低尺度，即低频信息；细节表示信号的高尺度，即高频信息。对含有噪声的信号，噪声分量的主要能量集中在小波解的细节分量中。在二元多分辨分析中，迭代分解过程使近似依次分解。原始信号在每个阶段的细节和近似能够被重建。典型的三层分解如图2 所示。

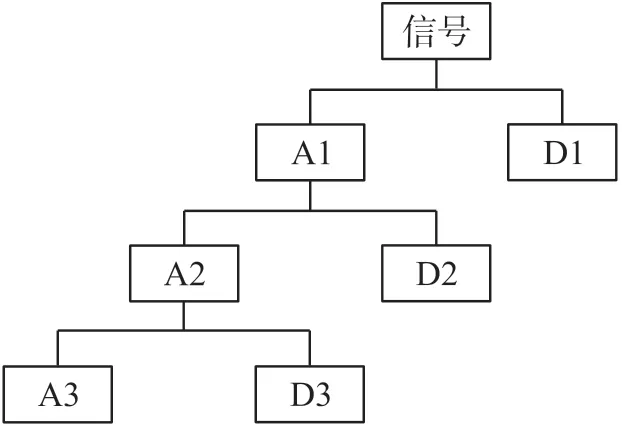
图2 典型三级分解离散小波变换结构

分解一直进行到单个细节仅包含单个样本为止。该过程的本质是生成一组向量A3、D3、D2 和D1，其中包含相应的系数。根据2 的幂，这些向量的长度依次增长。这些系数是信号给定尺度下在小波上的投影，它们由滤波器组在不同频带(A3、D3、D2 和D1)的信号组成。

典型的三级离散小波变换频谱分析如图3 所示。本文选择db1 进行分析。

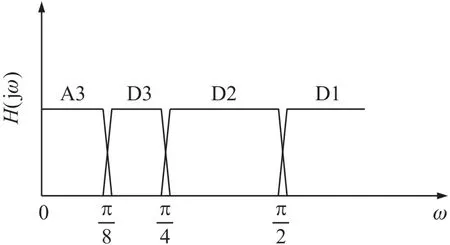
图3 三级离散小波变换频段分析

2 基于离散小波变换和相关系数的变压器内部故障判别方法

要进行离散小波变换分析，首先要选择母波和子波函数。母波的正确选择对检测和定位不同类型的信号变化起着重要的作用[6]。根据实际需要应选择不同的母波函数。扰动时间定位的精度随着尺度的增大而降低。子波的宽度和平滑度取决于子波的个数，因此，在选择合适的小波族及其数量时需要慎重考虑[8]。本文经过多次试验，选择了db1 母波。

本文提出的基于小波变换和相关系数的内部故障及励磁涌流检测方法主要分为离线和在线两个部分。

2.1 离线计算

当算法离线运行时，利用离散小波变换使用db1 母波对已知的励磁涌流信号进行分解。利用该信号生成一个指标，其定义为工频半周波内三相差动电流第5 级高频系数能量之和。

当小波基为正交基时，输入信号的能量可以表示为[9]:

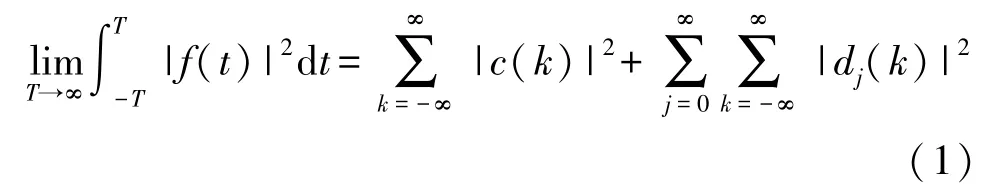
式中:dj(k)表示第j级的高频系数；c(k)表示频率为零的低频系数。

由帕塞定理可知，若使用的尺度函数和小波形成一组标准正交基，那么其展开分量的能量能与其小波系数联系起来。这意味着信号的范数或能量可以用其展开系数来分配[10-12]。因此第5 级高频系数的能量计算公式为:

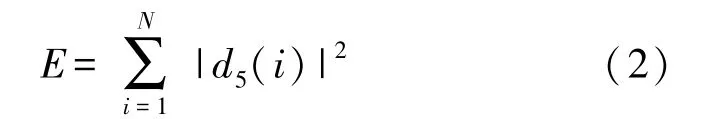
式中:d5和N分别为第5 级的高频系数及其相关系数的个数。

因此，将上述指标定义为第5 级高频系数的能量之和:

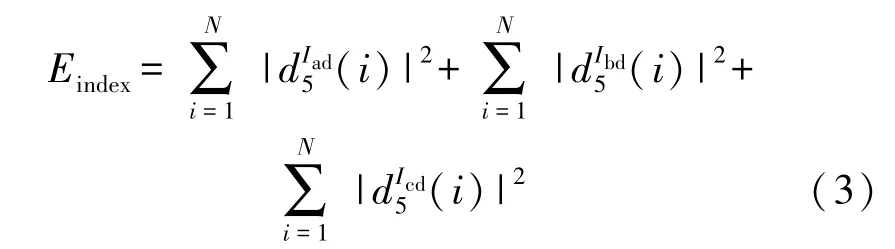
2.2 在线计算

本文对三相差动电流Iad、Ibd和Icd以10 kHz 进行采样，然后由采用db1 函数的离散小波变换对未知信号进行分解，最后计算其指标。未知信号的采样时间窗口为10 个工频半周波。计算预先存储的励磁涌流的指标与在线计算得到的指标之间的相关系数，当相关系数大于0.8 时，说明发生了励磁涌流，否则为内部故障(不同情况对比，结果表明不同种类内部故障电流与励磁涌流的相关系数均＜0.8)。其相关系数计算公式如下:

式中:Cov(E，Eindex)为预先存储的指标与在线计算指标的协方差；Var(E)为预先存储指标的方差；Var(Eindex)为在线计算指标的方差。

简化后的算法流程图如图4 所示。

图4 算法流程图

3 仿真结果及分析

为了获得所需的电流信号来研究本文提出方法的可行性，本文在MATLAB/Simulink 软件上进行仿真建模，仿真模型如图5 所示。

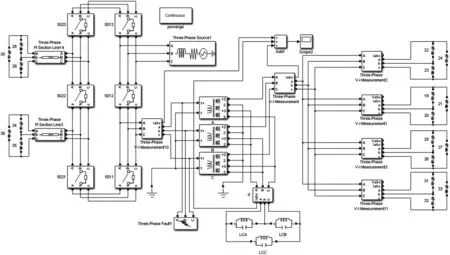
图5 仿真模型图

该模型为500 kV 变电站中典型的主变接线方式，主要由一台450 MVA、500/220/35 kV 的变压器以及输电线路构成，输电线路采用分布式模型。500 kV部分采用3/2 接线方式，两个断路器的总电流作为变压器的高压侧采样电流。

本文模拟了不同的内部故障和励磁涌流情况。并计算各个情况下指标随时间变化的波形。

图6 为三相差分励磁涌流的第5 级高频系数的能量之和的变化波形。从图中可以看出，在每个半周期内的指标数据是不同的。由此可以推断，对于不同情况的励磁涌流，其指标都应该有一个变化的过程。

图6 励磁涌流的第5 级高频系数的能量之和的波形

本文设置三相短路、两相接地短路、两相短路和单相短路的内部故障进行仿真，其指标变化如图7所示。

图7 各种故障下差动电流的第5 级高频系数的能量之和的波形

从图中波形可以看出，对于不同的内部故障，其三相差动故障电流的第5 级高频系数的能量之和经过一定的半周数之后，都能达到一个稳态值。但是相比于励磁电流，在不同的半周波内总是不断变化，这与内部故障有很大的区别。

此外，本文对不同的励磁涌流和内部故障电流进行了仿真。通过改变单相变压器剩余磁芯磁通(Br)、合闸相位角(θA)、二次绕组空载或带负荷以及强弱电源接入，模拟了不同情况下的励磁涌流。然后，利用本文提出的算法计算相关系数，计算结果如表1 所示，乘余磁通的负号表示方向，即增强或去磁方向。

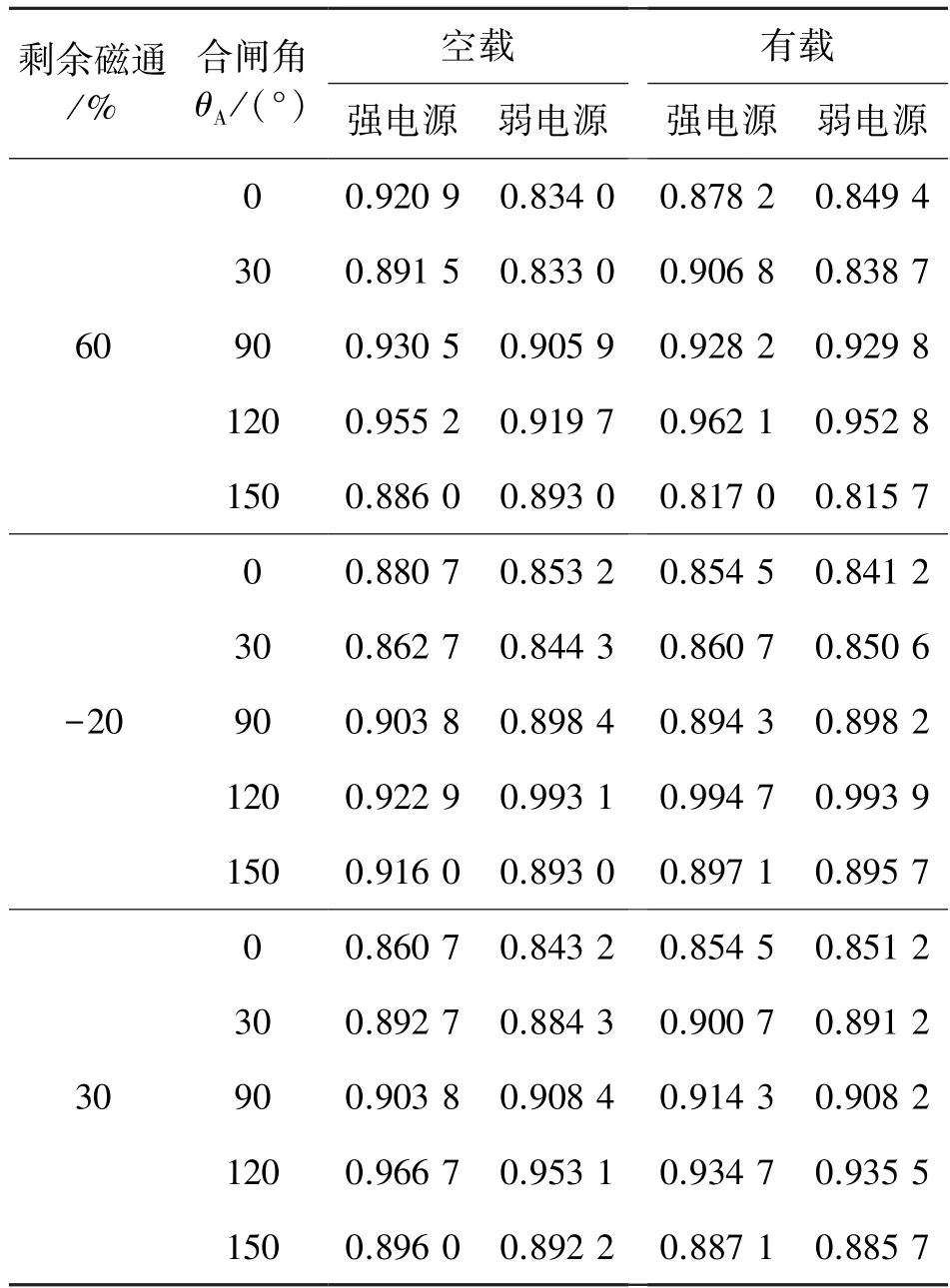
表1 不同情况下励磁涌流的相关系数

对于变压器内部故障，本文就故障电流特性的主要因素分别进行仿真，模拟了不同情况的故障电流。这些因素包括故障类型和有无带载条件，其相关系数的计算结果如表2 所示。

从表1 中数据可以看出，在任何励磁涌流情况下，其相关系数都大于0.8；而变压器发生内部故障时，其相关系数均小于0.8(表2)。因此，该判据能够有效区分出变压器是发生励磁涌流还是内部故障。

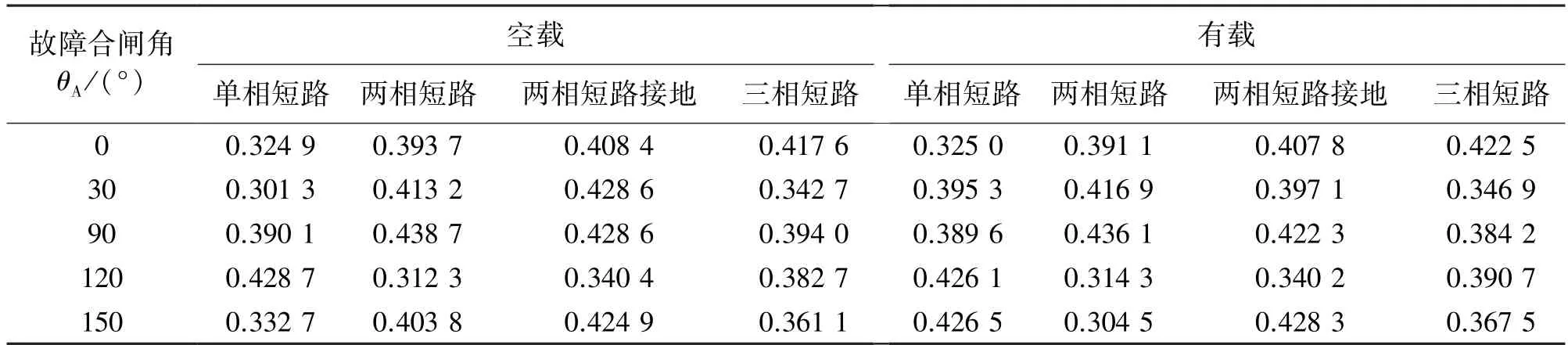
表2 不同内部故障情况下的相关系数值

4 结论

本文提出了一种判断励磁涌流和内部故障的新方法。该方法利用10 个半周波内三相差动电流第5 级系数能量和判断是否发生励磁涌流。经过10个半周波后，可将三相差动电流第5 级细节系数之和与预存励磁涌流信号的相关系数作为励磁涌流与内部故障的判别标准。如果相关系数大于0.8，则判断发生励磁涌流现象，否则为变压器内部故障。

该方法采用小波变换和相关系数的方法，避免了神经网络或模糊算法中需要训练和输入高维数变量的缺点。