空气静电放电的场路协同仿真研究*

王香霁，杨兰兰，杨 昌，王 倩，屠 彦

(东南大学电子科学与工程学院，江苏 南京 210096)

静电放电(Electrostatic Discharge，ESD)作为一种重要的电磁干扰源，对各种电气及电子设备的危害极大，静电放电的深入研究对静电放电的防护具有重要意义。静电放电模拟和测试研究通常分为接触放电和空气放电两种方式。接触放电方式具有较好的试验重复性，空气放电方式被认为可以更真实地模拟实际的静电放电过程，但这必须建立在空气放电的可重复性问题解决的基础之上。针对接触放电，国际电工委员会(International Electrotechnical Commission，IEC)提供IEC-61000-4-2 标准[1]，该标准对被测设备(equipment under test，EUT)的典型静电放电电流波形、测试电平范围、测试设备、测试设置和静电放电防护要求等相关的程序进行了规定。在接触放电模式下，放电电流与电荷电压成正比，因此，接触放电在时域和频域都可以被分析成线性系统。然而，由于电弧具有非线性特性，空气放电的数值模拟更加复杂，需要被建模为线性部分和非线性部分。德国研究者Rampe 和Weizel 提出了Rampe-Weizel 公式[2]，用来描述放电间隙作为等效电阻不满足欧姆定律的情况。David Pommerenke 团队考虑了空气放电模型中的非线性部分，采用SPICE (Simulation Program with Integrated Circuit Emphasis)模型来描述这一过程，从而研究空气放电的特性[3-4]。国内大量科研团队对空气放电过程中放电电压大小和极性、接近速度、温度和湿度对放电电流的影响做了大量的实验分析和验证，但空气放电的研究仍然缺少系统性和理论性。空气放电的仿真研究可模拟静电放电过程，并可实时监测静电放电过程中的电流和电磁场，从而能够预测并避免电磁干扰故障，是一种行之有效的ESD 研究方法。

本文基于场路协同仿真研究方法，首先通过静电放电发生器标准电流测试模型对该方法进行验证，然后利用该方法研究空气放电方式下放电电流随放电电压和弧长的变化，并与实验结果进行比较分析，对空气放电进行系统地研究。

1 场路协同仿真初步验证

场路协同仿真研究方法是一种可以对电磁场-电路耦合问题同时进行研究的方法，它将三维空间的电磁场信息以一个电路模块的形式链接到电路求解器中，通过端口在电磁场求解和电路求解之间设置建立一个接口，电压电流信息从电路求解器中流入场求解器中，可立即转化为电磁场信息，实现场路协同仿真研究真实物理场时空状态的变化。

本文利用商业电磁仿真软件CST，首先在微波工作室(microwave studio，MWS)中建立静电放电发生器的3D 全波仿真模型，添加端口之后将3D 模型场的信息作为一个路模块体现在设计工作室(DS)的路仿真器中，在DS 中添加电路元件可以进行场和路的交互，从而在DS 中建立场路协同仿真模型。之后，将静电放电发生器的3D 全波模型，场路协同仿真模型的结果和标准电流进行对比验证。

1.1 静电放电发生器3D 全波仿真模型

图1 所示为静电放电发生器的3D 全波仿真模型，该模型是基于人体金属模型的等效电路模型建立的。在静电放电发生器3D 全波仿真模型中包含3 部分:介质部分，如图中黑色部分，为有损介质，其相对介电常数为2，电导率为2 S/m；金属部分，如图灰色部分，其材料为完美电导体；集总电路元件，这些集总电路是贴附在线缆的端点处，主要与人体金属模型的电路参数相对应，见参考文献[5]。在3D仿真模型中的电压激励端口1 施加电压激励，在本节中为上升时间为1 ns 的8 kV 电压激励。

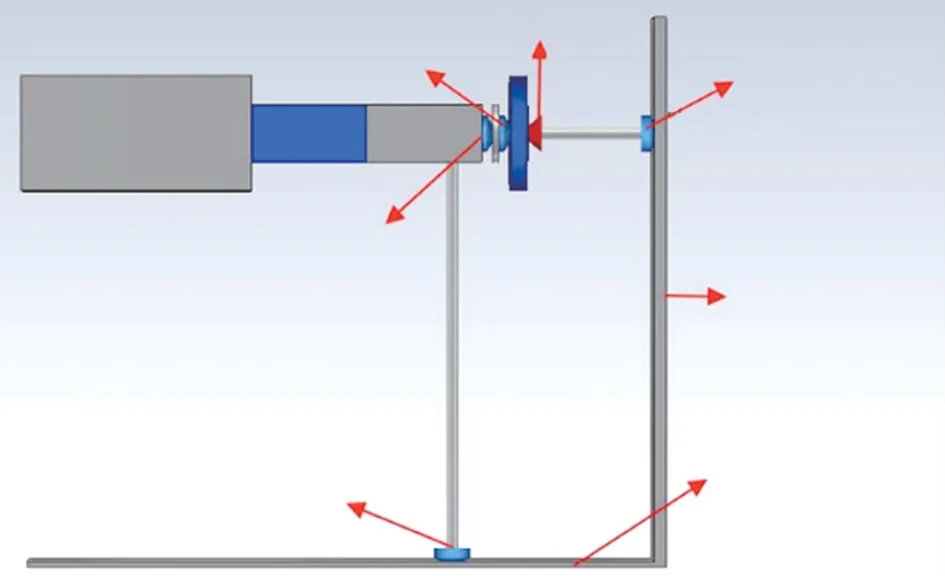
图1 静电放电发生器的3D 全波仿真模型

利用以上3D 模型，在CST 软件中进行仿真分析，仿真频率范围设置为0～500 MHz，accuracy 参数设定为-30 dB，边界条件Xmax和Ymin设置为Et＝0，其他都设置为open。

1.2 静电放电发生器场路协同仿真模型

为了对场路协同仿真方法进行验证，在CST MWS 中建立的静电放电发生器3D 全波仿真模型中接地线等效电感(400 nH)与放电头电感(20 nH)与接地板直接相连，在MWS 中将这两个元件替换成端口，从而获得与3D 模型场信息相对应的电路模块。图2 所示为静电放电发生器的场路协同仿真模型，该模型包含与3D 模型场信息相对应的电路模块，该模块包含三个端口，其中端口2 和端口3 为本仿真特意去除电感位置处所设置的端口，在DS 工作室中的对应位置连接对应电感元件并接地，端口1 为电压激励端口，与图1 中的电压激励端口相对应，仍设置为上升时间为1 ns 的8 kV 电压。

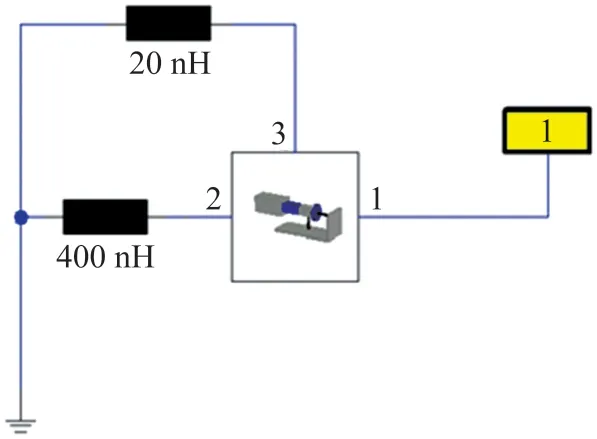
图2 静电发生器的场路协同仿真模型

在CST DS 仿真任务中设置仿真时间为60 ns、激励电压为8 kV、上升时间1 ns，且仿真方式选择CST MWS Co-Simulation。图3 所示为MWS 3D 全波仿真模型、DS-MWS 场路协同仿真模型计算所得的放电电流和IEC 标准电流的对比结果。

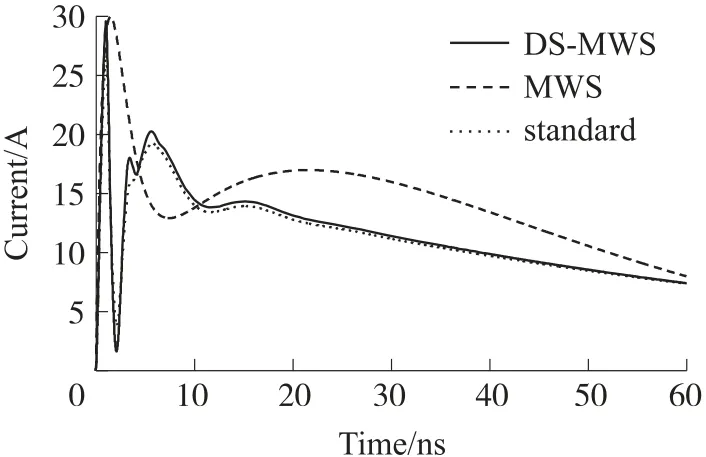
图3 8 kV 下放电电流波形对比

从图3 可知，在MWS 3D 全波仿真模型和DS-MWS 场路协同模型这两种方式下仿真结果吻合很好，相较于标准放电电流的两个波峰变化更加剧烈。根据标准波形所规定的放电电流在第一个波形、上升时间30 ns 处电流与60 ns 处电流的情况，仿真波形仍然是满足标准放电电流条件。表1 对两种仿真方式下的结果与IEC 标准中规定的4 个参数的参考值进行了对比。两种方式下的仿真波形均在规定的误差内，满足IEC 标准规定的参数数值，这证明了场路协同仿真方法可以满足静电放电的研究要求。经过比对两种仿真结果，可以推断，在CST MWS 中设置端口获得与3D 场信息相应的电路模块后，在CST DS 中添加电路元器件进行路的仿真和场的仿真交互是可行的。因此可以将场路协同方法应用到空气放电的研究中，通过加入非线性电弧的SPICE 模型进行空气放电的场路协同仿真研究。

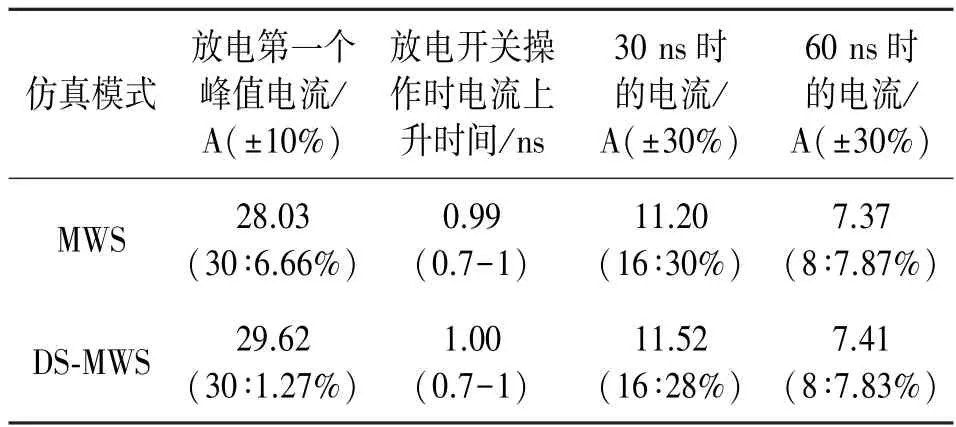
表1 IEC61000-4-2 标准波形与仿真波形数值对比

2 空气静电放电场路协同仿真模型

图4 所示为空气静电放电场路协同仿真模型。

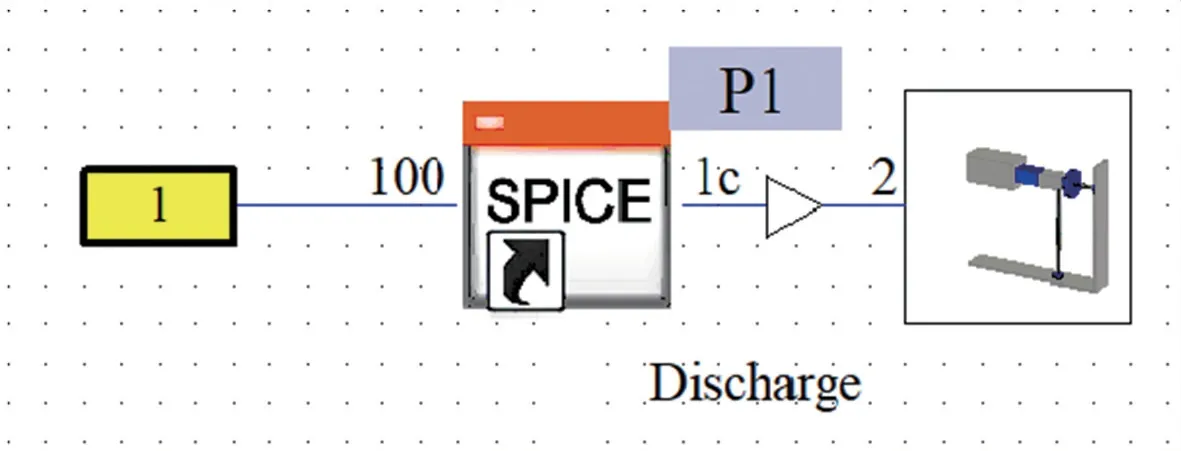
图4 空气静电放电场路协同仿真模型

首先利用如图1 所示的3D 全波仿真模型，通过设置空气放电弧端口2 建立对应3D 场模型的电路模块，该模块通过端口2 和描述空气放电的Rompe-Weizel SPICE 模型相连，SPICE 模型结构参考文献[6]，该SPICE 模型描述了Rompe-Weizel 规律，公式如下[7]:

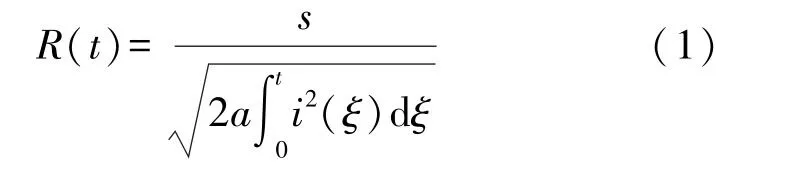
式中:R(t)为火花电阻，Ω；s为火花长度，m；i为放电电流，A；a为经验常数，取(0.5～1)×10-4m2/V2s。

SPICE 模型将Rompe-Weizel 公式描述成电路结构，他是一个非线性网络。火花电阻在放电初期，电阻趋近于无穷大，空气击穿过程中电阻迅速减小，同时与火花长度成正比，即放电弧长越大，电阻越大。该模型的本质就是描述了空气放电过程中电压电流随弧长和时间的非线性变化关系。如图4 中给SPICE 左侧的端口添加激励，探针P1可监测空气放电电流，从而研究电压和弧长对放电电流的影响。

该仿真模型使用上升时间约为30 ps 的阶跃函数作为激励源。上升时间的选择有以下考虑:如果时间过长，则会影响电流上升时间，电流上升时间仅由电弧电阻定律和线性等效电路决定；上升时间不能太小，如果脉冲中包含的强频率成分超过了计算阻抗的范围，就会导致SPICE 模拟中的不稳定性。快速的电压上升启动了电弧电阻模型，因此采用上升时间为30 ps 的SPICE 电弧模型。

3 空气静电放电仿真结果及分析

3.1 空气静电放电电流

利用如图4 所示的空气静电放电场路协同仿真模型，分别仿真固定放电电压5 kV 和固定弧长0.5 mm 时，探针P1 端监测的放电电流。

3D 全波仿真模型与电弧模型相结合，从图5 和图6 中，可以清晰地看出激励电压和放电电弧的长度对峰值电流和上升时间有着重要影响。图5 给出了在5 kV 激励电压下、不同放电电弧下的模拟放电电流，随着放电弧长的增加，放电电流的峰值是减小的，上升时间增加，图中表现为放电电流的峰值逐渐变得平坦，尤其在0.7 mm 以上第二峰的高度超过第一峰。图6 展示了0.5 mm 弧长下不同放电电压下的电流图，随着激励电压减小，弧长不变时，放电电流减小，上升时间增加，仿真结果与参考文献[8]的实验结果是相符的。

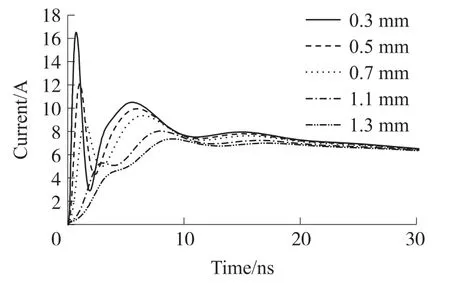
图5 5 kV 不同弧长下的放电电流波形图

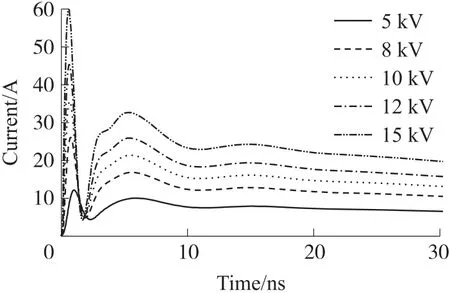
图6 0.5 mm 弧长不同电压下的放电电流波形图

场路协同仿真是让电压电流从CST DS 工作室流入CST MWS 工作室所仿真的3D 无源结构中转化为电场与磁场的仿真方法，可以展现出不同时刻整个空间的电磁场。图7 为激励电压5 kV 弧长0.3 mm 下的电磁场分布。由图5 所示弧长为0.3 mm时的放电电流波形可以看出放电时间为1 ns左右的电流变化最剧烈，图7(a)和图7(b)分别为1 ns时的3D 空间的电场模和磁场模分布情况。从图7 可以看出，放电枪头和接地带的电场强度达到整个空间的最大值，约为105V/m 数量级大小，而磁场强度可以达1 000 A/m。若此3D 全波模型中加入待测印刷电路(PCB)，则可以实时监控PCB 板上的电磁场分布情况，为PCB 板上的故障检测提供指导。

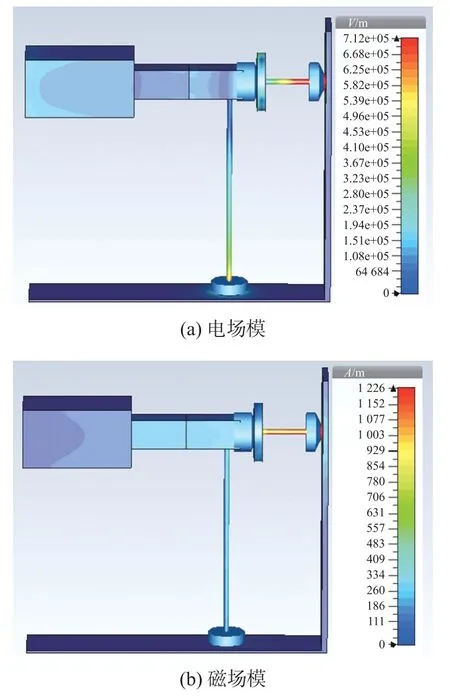
图7 5 kV 激励电压弧长0.3 mm 下1 ns 的电磁场分布

3.2 放电弧长对放电电流的影响

放电弧长对于空气放电影响表现在峰值电流上升时间和峰值电流大小上。放电弧长选取0.3 mm、0.5 mm、0.7 mm、1.1 mm 和1.3 mm，探究在不同激励电压下放电电流的情况。

静电放电研究中，峰值电流上升时间和峰值电流幅值是重要的研究因素。从图8 和图9 可知，在一定电压范围内，激励电压相同时，随着放电弧长的不断增大，峰值电流不断减小，同时上升时间不断增大。不同激励电压下的上升时间tr和峰值电流Ip的变化情况，我们可以用指数式(2)和式(3)进行拟合计算:

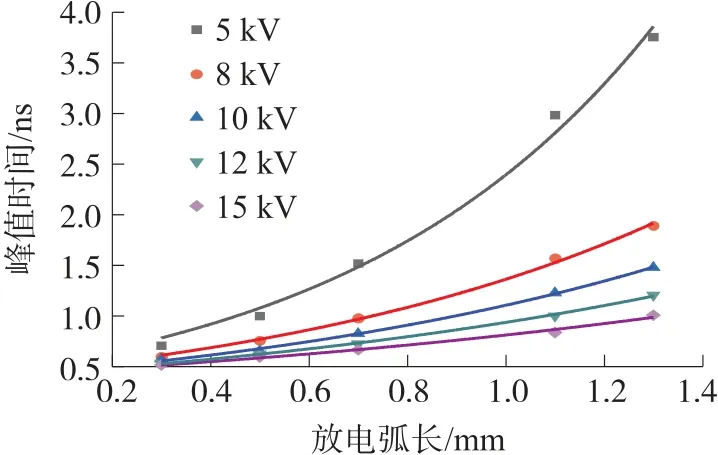
图8 不同激励电压下随着放电弧长不同峰值时间变化曲线

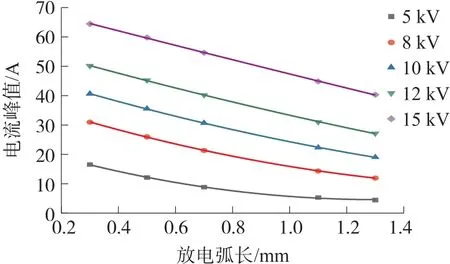
图9 不同激励电压下随着放电弧长不同电流峰值变化曲线

式中:tr为上升时间；Ip为峰值电流；s为弧长的大小。

表2 和表3 中的公式拟合的拟合优度Adj.R-Square 的值都趋近于1，说明拟合结果是理想的。从图中波形变化趋势和拟合公式的参数来看，在电压固定时，峰值电流上升时间随着电弧长度的增加呈指数增加，并且随着激励电压的增加，拟合曲线变化的比例系数不断减小，如表2 中参数b1所示。电压固定时，电流峰值随着电弧长度的增加而指数递减，且随着激励电压的增加，拟合曲线变化的比例系数减小，如表3 中b2的绝对值所示。拟合曲线与放电弧长的指数变化关系的比例系数，如表2 和表3中的b1和b2，应该是与空气放电时电弧空间的电场作用时间相关的一个参数，激励电压越高，电弧空间的电场强度越大，电子漂移时间会减小，受电场影响的时间更短，因此上升时间的拟合比例参数b1和峰值电流的拟合比例参数b2的绝对值会减小。

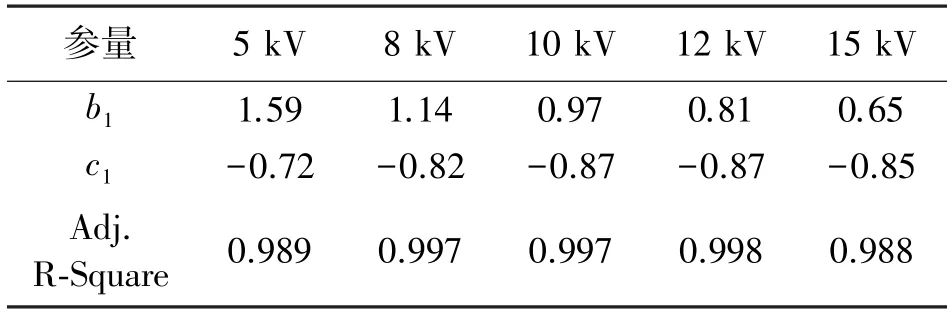
表2 不同激励电压下上升时间的拟合公式参数

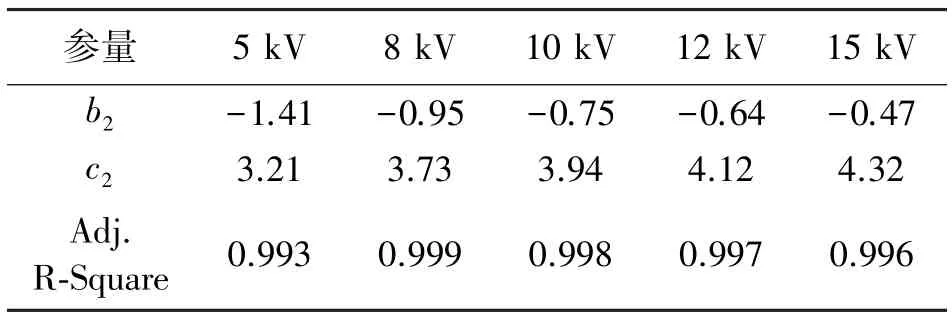
表3 不同激励电压下电流峰值的拟合公式参数

放电弧长的变化可以与接近速度相比拟，当电压一定时，接近速度越快，放电弧长越短，放电电流的上升时间和峰值随着弧长的变化与随着接近速度的变化趋势是相同的。参考文献[9]中的实验结果指出了放电的电流峰值随接近速度的增加而增加，但这一变化并不是线性的，利用该文献中5 kV 下不同接近速度下峰值电流实验结果进行拟合，拟合公式如(4)所示:

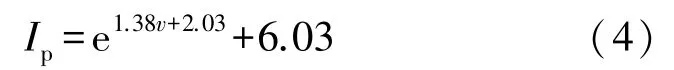
式中:Ip为峰值电流；v为电极的接近速度。

从上述公式可以，看出该实验结果和我们仿真结果一样符合指数变化规律的。而且5 kV 下的比例系数为1.38，也和我们仿真的比例系数b2＝-1.41 的绝对值非常接近。

3.3 激励电压对放电电流的影响

激励电压选取5 kV、8 kV、10 kV、12 kV 和15 kV，探究在不同放电弧长下放电电流的情况。

从图10 和图11 可知，在一定弧长范围内，放电弧长相同时，随着激励电压的不断增大，峰值电流不断增大，同时上升时间不断减小。对于不同放电弧长下上升时间和峰值电流，分别用不同的公式进行拟合计算，其中式(5)是拟合激励电压和上升时间关系，式(6)是拟合小弧长下激励电压和峰值电流关系，同时式(7)可以拟合大弧长下激励电压和峰值电流关系:

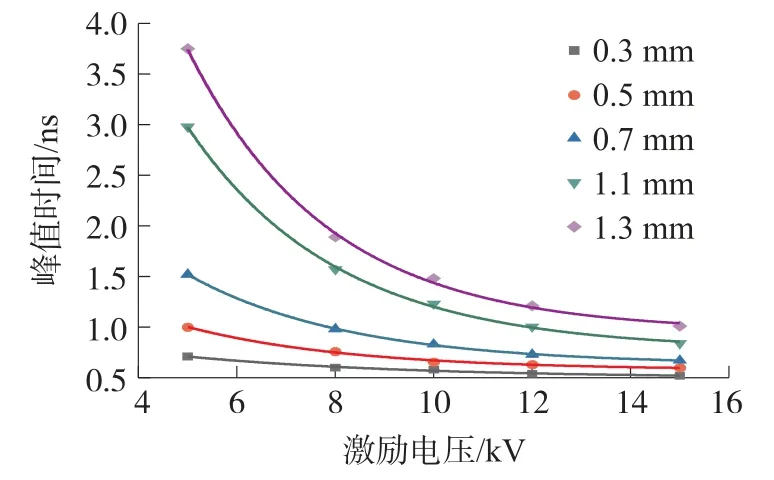
图10 不同放电弧长下随着激励电压不同峰值时间变化曲线

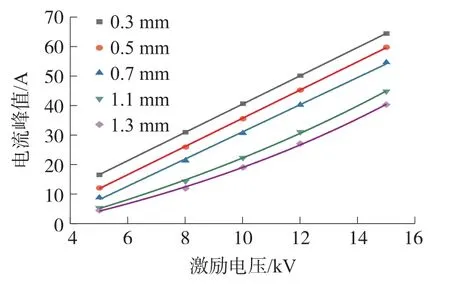
图11 不同放电弧长下随着激励电压不同峰值电流变化曲线

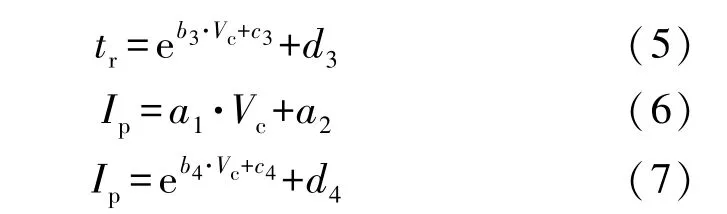
式中:tr为上升时间；Ip为峰值电流；Vc为放电电压。

表4 和表5、表6 中的公式拟合的拟合优度Adj.R-Square 的值都趋近于1，说明拟合结果是理想的。从图10 和图11 的波形变化趋势和拟合公式的参数来看，在电弧固定时，峰值电流上升时间随着激励电压的增加呈指数减小，并且随着放电弧长的增加，拟合曲线的比例系数也不断增加，对应着表4 中的b3的绝对值。从图11 中的拟合曲线来看，小弧长0.3 mm 和0.5 mm 下，峰值电流的变化曲线用线性公式进行拟合，而随着电弧长度的增加，变化情况逐渐呈指数化。从图5 的5 kV 电压下不同弧长的放电电流可知，在小弧长下，空气放电电流和IEC 标准下静电放电电流波形类似，电流峰值随电压的变化趋于线性变化，即非线性因素影响较小。在参考文献[10]中通过模拟和实验证明接触放电情况下，峰值电流随激励电压的增加线性增加，空气放电小弧长情况下与接触放电相近，接近于线性，而弧长大时，非线性因素就比较明显了。此仿真模拟结果已经在原青云[11]经过大量的实验验证，对一定电压范围内的实验结果进行拟合，得出不同电压下的峰值电流式(8):

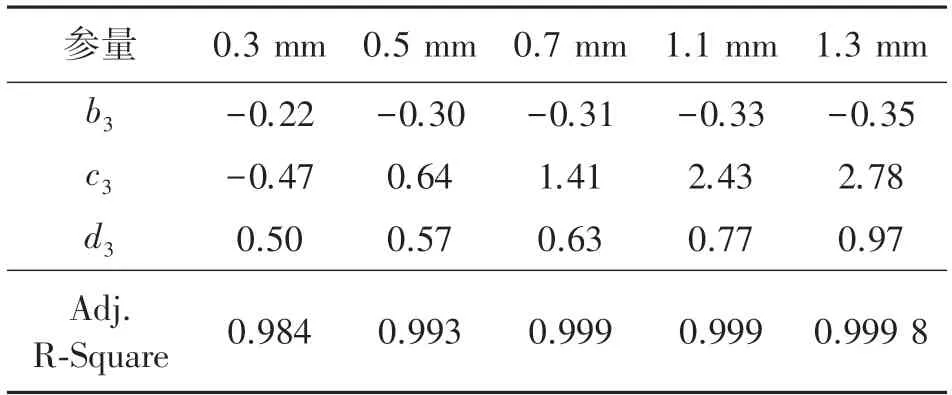
表4 不同放电弧长下上升时间的拟合公式参数

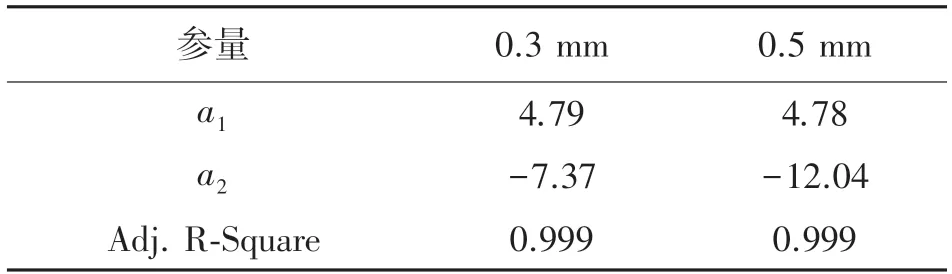
表5 较小放电弧长下电流峰值的拟合公式参数

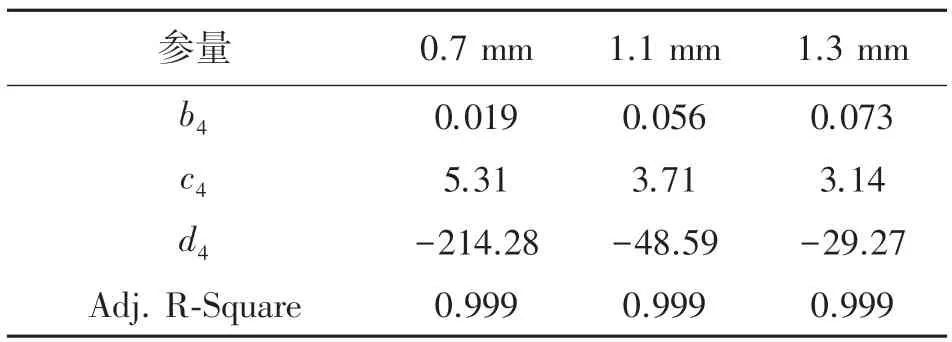
表6 较大放电弧长下电流峰值的拟合公式参数

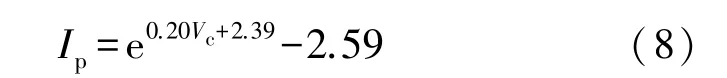
式中:Ip为峰值电流；Vc为激励电压。

从上述公式可以看出，我们仿真结果也符合指数变化规律。在0.7 mm 以上的大弧长下，电流峰值随着激励电压的增加而指数增加的，且随着放电弧长的增加，拟合曲线的比例系数增加。而拟合曲线和激励电压指数变化关系的比例参数，如表4 和表6 中的b3和b4，应该是与空气放电时整个电弧空间的电场作用时间相关的一个参数，放电弧长越长，放电间隙越大，空间电荷发生碰撞和电离的范围越大，电荷在电场内漂移的时间越长，受电场影响时间长，因此上升时间的拟合比例参数b3绝对值和峰值电流的拟合比例参数b4的绝对值会增大。

3.4 激励电压、电流峰值和上升时间的关系

在实际的实验测试过程中，放电弧长大小是随着激励电压的变化而变化的。为了模拟更加真实的实验过程，标准条件下空气放电的临界击穿电压和临界间隙公式为[12]:

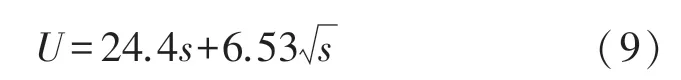
式中:U为击穿电压，kV；s为放电间隙，cm。

图12 是场路协同仿真得到不同电压下放电电流波形，此时的放电弧长是利用式(9)计算所得。从图12 中可以知道，随着激励电压的增加，上升时间不断增加，电流波形的前沿逐渐平坦，甚至逐渐消失成只有第二峰的波形。出现这一现象的原因可能是激励较高的时候放电弧长较长，那么电磁能量会在更长时间里释放。

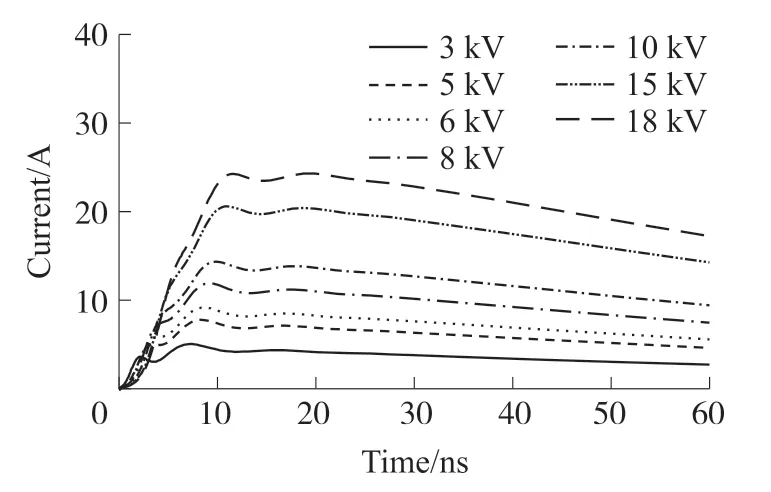
图12 不同电压下空气放电电流

在图13 中不同放电电压下测量了第一峰值的上升时间tr和电流峰值Ip，对于这些放电电流的参数做了拟合如图13 中所示。图13 给出了激励电压Vc、电流峰值Ip和上升时间tr的拟合式(10)如下:

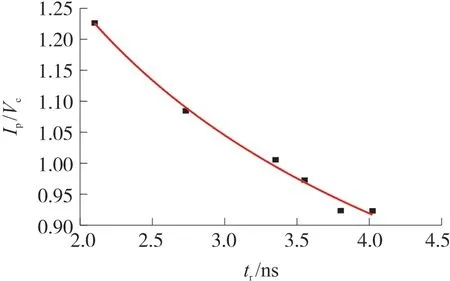
图13 激励电压Vc、电流峰值Ip 和上升时间tr 的关系

通过这个公式可以得出:空气放电电流峰值Ip与激励电压Vc比值与上升时间成反比。在同一放电电压下，放电电流的峰值与上升时间的幂指数成反比，即随着上升时间增加，波形前沿平坦，放电电流的峰值逐渐减小。由于波形前沿陡峭，放电峰值越大，产生的电磁场能量越大。该仿真结果在徐晓英[13]的大量实验中得到验证。

4 结论

本文利用场路协同仿真方法对空气静电放电进行仿真分析。首先利用静电放电发生器的标准电流测试进行场路协同仿真验证，得到了较为理想的结果，表明在CST MWS 中设置端口获得与3D 场信息相应的电路模块后，在CST DS 中添加电路元器件进行路的仿真和场的仿真进行交互是可行的，从而使得包含非线性元素的空气放电的仿真成为可能。然后采用控制变量法对空气放电过程中激励电压和放电弧长的影响进行研究，得出放电上升时间和峰值电流均随着激励电压和弧长指数变化，而小弧长情况下与接触放电类似接近线性变化。由于在实际的空气放电的实验过程中，激励电压的大小会影响放电弧长的长短，所以通过激励电压和弧长公式再次模拟得出激励电压Vc、电流峰值Ip和上升时间tr的关系曲线，并通过公式进行拟合发现，上升时间的幂指数与峰值电流和放电电压的比值成反比关系，仿真结果与文献中的实验结果吻合。

本文场路协同仿真所建立的SPICE 电路简化模型描述了空气放电过程中的电弧，实现了对空气放电的仿真分析，模拟验证了空气放电具有区别于接触放电的非线性特征。然而本文的仿真分析对空气放电的描述还比较简单，还未考虑温湿度、气压以及空气流体力学变化等各方面的影响因素，因此还需要进一步通过实验或流体动力学模型探究空气放电的特性，来完善SPICE 模型。这种场路协同仿真分析方法在分析电路特性的同时，还可以实时监控空间中的电磁场特性，这一特点对后续分析包含印刷电路板的电子设备的硬故障和软故障检测具有极大的优势。