基于TIR 透镜的LED 光源准直输出探究

秦 晋，秦会斌，邱定忠，叶 晨

（杭州电子科技大学 电子信息学院，浙江 杭州 310018）

0 引言

随着社会的高速发展，LED 作为一种新型光源也在快速发展，目前已经成为了一项具有发展前景的技术产品。 与其他光源相比，LED 具有高亮度、寿命长、功耗低、价格低廉、节能环保等诸多优势，被广泛应用在路灯、照明、医学及显示等领域[1～4]。 对于一般的LED 光源，出射光分布遵从朗伯型分布，其发散角约为120°，发散角大，如果直接应用，光能利用率低，且很难满足一些照明场合需要达到的性能指标，如均匀度、亮度等[5]。为了解决上述问题，需要给LED 光源进行二次光学设计， 那就是给LED 配光来控制光线输出方向，减小发散角，提高光能利用率。

基于非成像光学理论的系统光学设计已经成为了当下人们研究的热点，相关设计方法也在逐渐完善。 常用的设计方法主要分两大类：一类是针对点光源的设计，如裁剪法、偏微分方程法、数值分析法等；另一类是针对面光源的设计，如同步多曲面设计法[6～9]。

本文根据边缘光线原理及同步多曲面设计法设计了一种基于全内反射（TIR）透镜的准直系统，通过TIR 透镜控制光线输出方向， 对光线进行准直，提高光能利用率。 然后利用光学软件Tracepro对光线进行追迹仿真，根据追迹结果来反馈并优化设计，最终达到最优准直效果。

1 TIR 透镜的设计

TIR 透镜的设计目的在于控制光线输出方向，减小光束的发散角，达到准直效果，实现均匀、高亮度的照明，同时提高光能的利用率。

TIR 透镜的工作原理图如图1 所示。由于LED具有旋转对称性， 透镜曲面可由AB段、BC段、CD段、DE段、EF段和FA段构成的横切面绕对称轴EF旋转360°构成。 LED 光源位于中心点O点，大角度的光线由AB旋转面全反射成为平行光，再经过FA旋转面射出； 小角度的光线由DE旋转面折射成为平行光，再经过FA旋转面射出，从而达到准直的效果。 在设计中，BC段为直线段，不起光学作用，长度为0.2mm，进行固定；CD段可以稍微倾斜，便于模具制造。

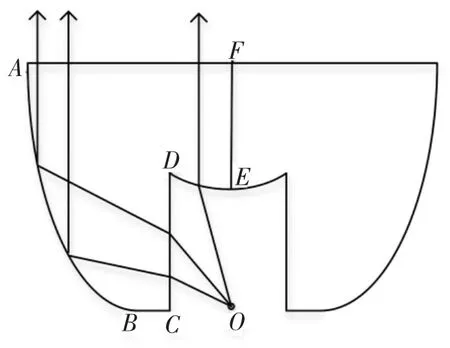
图1 TIR 透镜的工作原理图Figure 1 Working principle diagram of TIR lens

1.1 内折射面的设计

内折射面的设计示意如图2 所示，LED 光源位于O点。P1点为内折射面的最低点，该点位于LED光源的正上方的主轴上， 设其对应坐标为（0，y1，0），N1为P1点的法向矢量，N1的方向垂直向上。然后根据第一个点推算出第二个点的坐标。 以N1为法线矢量，过P1点作切平面，该平面为与水平面平行的平面， 它与入射角为θ1的光线相交于点P2（x2，y2，0）。 设入射角为θ1的光线的方向矢量为I，其归一化的坐标为（cos（θ1），sin（θ1），0），由于TIR透镜起到准直效果， 所以光线会垂直向上出射，设出射矢量为O（0，1，0）。 将光线入射矢量I 及出射矢量O 代入到斯涅耳（Snell）定律中（式1），就可以求出P2点的方向矢量N2。 其中n为光入射介质折射率与出射介质折射率的比值， 因为介质为空气，折射率可看成是1，所以n就是TIR 透镜光学材料折射率的倒数[10]。

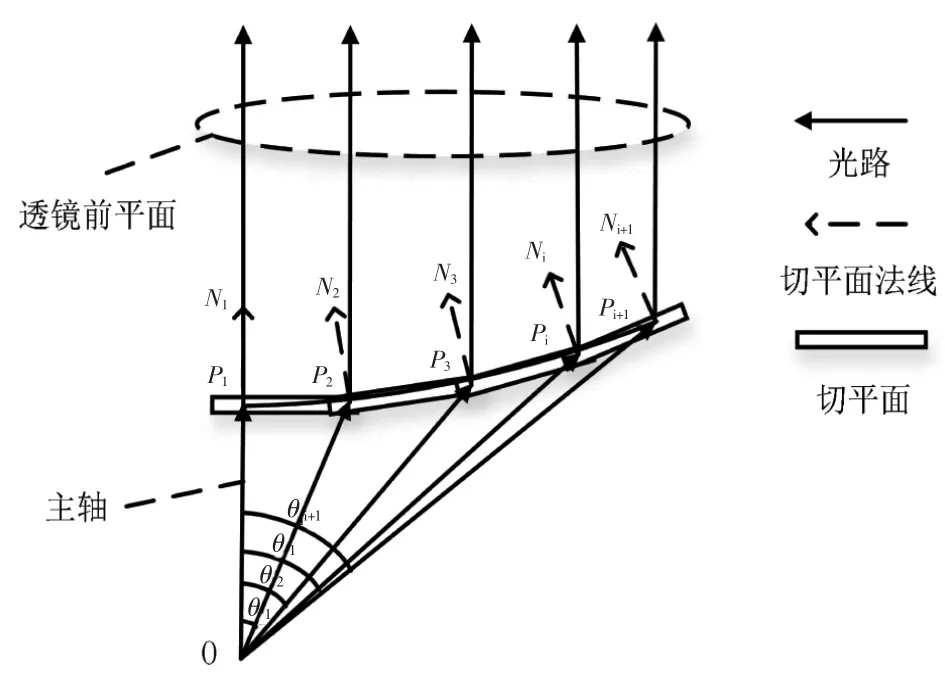
图2 内折射面的设计示意图Figure 2 Schematic diagram of the design of the internal refractive surface

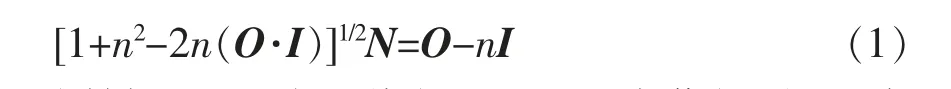
同样，以N2为法线矢量，过P2点作切平面，该平面与入射角为θ2的光线相交于P3（x3，y3，0），再将入射角为θ2的光线的入射光线和出射光线的方向矢量归一化坐标I2（cos θ2，sin θ2，0）和O2（0，1，0）代入到Snell 定理（式1）中即可求得P3点的法向矢量N3。

通过采用这种方法可以由第i个点Pi点的坐标（xi，yi，0）、法向矢量Ni、入射矢量归一化坐标Ii（cos θi，sin θi，0）及出射矢量归一化坐标Oi（0，1，0）求出曲线下一个点Pi+1的坐标（xi+1，yi+1，0），从而求出内折射面的轮廓曲线。

1.2 侧面全反射面的设计

侧面全反射面的设计如图3 所示，LED 光源位于O 点。 P1点为侧面全反射面的最低点，该点位于光源水平横轴上，设其坐标为（x1，0，0），N1为P1点的法向矢量， 其方向与主轴成45°夹角，P1点的横坐标减去不起光学作用的固定长度0.2mm 即为全反射面的内半径R0， 然后根据第一个点推算第二个点的坐标。假设已知第二条光线与水平轴之间的夹角为θ1，以N1为法线矢量，过P1点作切平面，该平面与水平面成45°夹角，它与入射角为θ1的光线相交于P2点，其坐标为（x2，y2，0）。设入射角为θ1的入射光线的方向矢量为I， 其归一化的坐标为（cos θ1，sin θ1，0），由于TIR 透镜的准直作用，所以出射光线会竖直向上，设出射光线矢量归一化坐标为O（0，1，0）。 将入射矢量I及出射矢量O代入到Snell定律（公式2）中，就可以求出P2点的方向矢量N2。其中n 为透镜光学材料折射率的倒数。

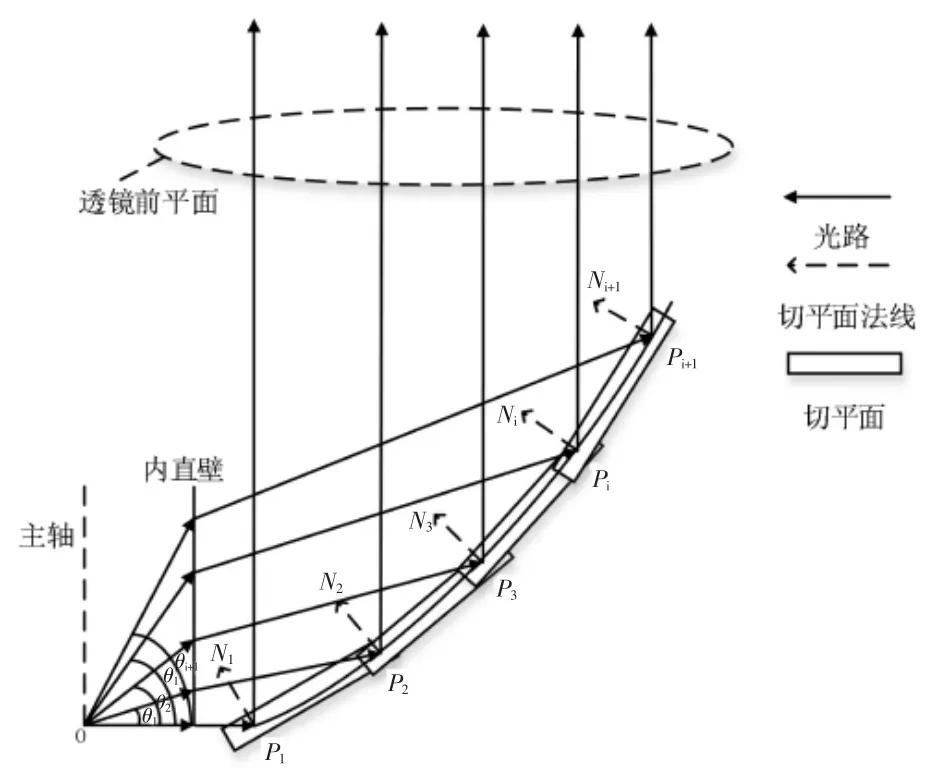
图3 侧面全反射面的设计示意图Figure 3 Schematic diagram of the design of the lateral total reflection surface

在求出P2点法向矢量后， 同样以P2点的法向矢量N2为法线矢量，过P2点作切平面，其平面与入射角为θ2的光线相交于P3（x3，y3，0），再根据入射角为θ2的光线的入射矢量I2（cos θ2，sin θ2，0）和出射矢量O2（0，1，0）以及Snell 定律求出P3点的法向矢量N3。

通过采用这种方法可以通过由第i 个点Pi的坐标（xi，yi，0）、法向矢量归一化坐标Ni、入射矢量归 一 化 坐 标Ii（cos θi，sin θi，0） 及 出 射 矢 量Oi（0，1，0）求出曲线下一个点Pi+1的坐标（xi+1，yi+1，0），从而求出全反射面的轮廓曲线。

通过上述设计方法得到两条由一系列离散点组成的轮廓曲线，将这些离散点导入到SolidWorks中并采用坐标点放样生成曲线的方法进行拟合生成实体轮廓曲线，然后将实体轮廓曲线绕主轴旋转360°即可得到TIR 透镜的三维模型。

2 模拟仿真

根据上述设计所得的TIR 透镜三维模型如图4 所示。

图4 TIR 透镜的三维示意图Figure 4 Three-dimensional schematic diagram of TIR lens

将该实体模型导入光学软件Tracepro 中进行模拟仿真，TIR 透镜的光学材料采用PMMA， 其折射率为1.4935， 设置LED 光源为点光源后进行光线追迹， 其光线追迹如图5 所示。 从图可以看出，LED 光源发出的大角度的光线及小角度的光线通过TIR 透镜都能准直输出。

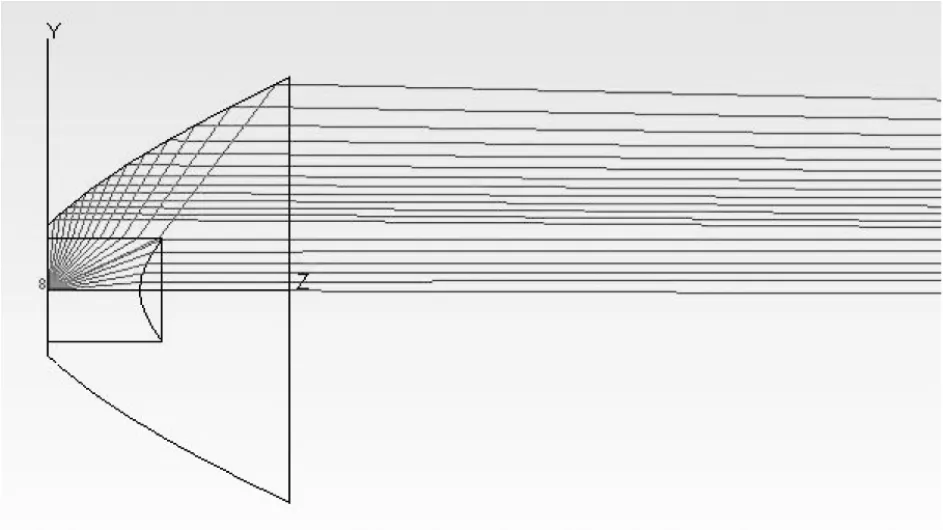
图5 点光源下的光线追迹图Figure 5 Ray tracing diagram under point light source

设置LED 光源为档案光源， 档案光源采用CREE 公司的XLamp XPE 光源。 设置好接收面后对LED 光源的出射光线进行光线追迹， 其光线追迹如图6 所示。

图6 档案光源下的光线追迹图Figure 6 The ray tracing diagram under the file light source

从图中可以看出，LED 光源发出的光线经TIR透镜配光后，光束基本达到准直效果。

图7 和图8 分别为接收面上的照度分布图和发光角度分布图。由图可以看出TIR 透镜的光能利用率为90.33%，接收面上光斑均匀，光束的发散角较小，大致集中在±8°以内。

图7 照度分布图Figure 7 Illumination distribution map

图8 发光角度分布图Figure 8 Luminous angle distribution diagram

3 结语

本文根据边缘光线原理及SMS 法设计了一种基于TIR 透镜的准直系统，通过该系统控制光线输出方向、准直光线，并通过Tracepro 对设计的实体模型进行仿真模拟。 其光能利用率为90.33%，光束发散角在±8°左右。仿真结果表明，在该结构相对简单的准直系统下，光能利用率高，且有效地对LED光源的输出光线进行了准直。