基于S 曲线的前馈三闭环PID 伺服控制器设计

李万宝，田 达

（中电海康集团有限公司，浙江 杭州 310012）

0 引言

随着科学技术水平的不断提高，伺服驱动器的性能有了极大地提高。 伺服驱动器也向着数字化、智能化、小型化、通用化方向发展[1]。目前，伺服控制技术在智能机器人、机械加工、数字机床等方面越来越重要，面向机器人关节、智能制造等小型化伺服控制器也逐渐成为研究的重点[2]。与此同时，这些领域也对小型化伺服控制器的响应速度、控制精度等提出了更高的要求。目前普通伺服控制器一般采用位置环、速度环、电流环的三闭环PID 控制，但是存在超调大、响应速度慢等缺点[3]。文献[4]提出采用速度加速度双前馈控制技术，提高了系统响应速度和跟踪特性，但采用位置指令进行微分运算，计算复杂度较大。

本文提出了采用S 曲线结果提取速度及速度前馈补偿的方法， 并由此研究出基于ARM7 内核的低压交流伺服驱动器，具有以下特点：采用microchip32 位数字控制器ATSAME70N21B， 运算速度400MHz， 并支持Ethernet，CAN，UASRT 等多种通讯方式；低电压输入，最高支持500W 输出；采用三闭环控制，其中基于S 曲线优化前馈控制，提高控制器的实时响应速度和控制精度。

1 系统硬件设计

系统整体硬件方案如图1 所示。整个系统包括了控制模块、电机驱动模块、信号采集模块、通讯模块、电源模块等。 控制模块选择ARM7 内核3ATSAME70N21B 进行开发。通过电机驱动电路实现整体的回路控制功能，包括：三相永磁直流伺服电机的驱动，主控输出PWM 后通过专用的驱动电路驱动MOS 管实现通、断功能，根据电机不同的位置驱动电机运转；专用的反馈电路，实现电机闭环控制功能，支持相对编码器和霍尔传感器；通讯、调试端口，用于控制和调试，包括SWD，USB，CAN，RS232等；温度传感器、E2PROM 等实现温度读取、数据存储等。

图1 伺服驱动硬件设计Figure 1 Servo drive hardware design

1.1 伺服电机驱动电路设计

三相永磁直流伺服电机的驱动采用MIC4605芯片，主控输出PWM 后通过专用的驱动电路驱动MOS 管实现通、断功能，根据电机不同的位置驱动电机运转。 伺服电机驱动电路设计如图2 所示。

图2 伺服电机驱动电路Figure 2 Servo motor drive circuit

1.2 反馈电路设计

反馈电路包含电流电压检测、传感器、编码器等，实现电机闭环控制功能。

第一，三相电机的相电流检测、总电流检测。通过高精度采样电阻采样各相流过的电流，反馈给主控实现FOC 电流环控制功能，如图3 所示。

图3 电流检测示意图Figure 3 Schematic diagram of current detection

第二，HALL 传感器的反馈。HALL 传感器集成在电机内部， 通过给主控提供起始位置信息等，实现电机启动端的控制。霍尔传感器反馈电路设计如图4 所示。

图4 霍尔传感器反馈电路设计Figure 4 Hall sensor feedback circuit design

第三，编码器的反馈。编码器集成于电机内部，通过给主控提供电机精准的绝对位置信息等，实现电机运转过程中的精确位置反馈功能。编码器反馈电路设计如图5 所示。

图5 编码器反馈电路设计Figure 5 Encoder feedback circuit design

2 系统软件架构设计

2.1 软件整体架构

伺服器软件架构整体分为应用层、 设备驱动层、平台驱动层和通用库四大模块。 从上到下依次为应用层、设备驱动层和平台驱动层。 最上层为应用层，它是根据设备驱动层提供的数据，依据既定逻辑进行判断和控制，包含电机控制模块、外部软件监控模块、通信控制模块、故障与处理模块等；中间层为设备驱动层，它是根据平台驱动层提供的信息为应用层提供数据，或者从应用层接收指令控制平台驱动层的模块，包含三环控制模块、位置采集、电流电压温度采集、FOC 控制算法和SVPWM 控制算法；最底层为平台驱动层，它是直接使用硬件资源的模块，如UART，QDEC，IO，ADC，PWM 和定时器等模块。 另外还有通用库模块，为某些功能提供集成的调用，包括CRC 校验、PID 控制和三角函数等模块。 如图6 所示为伺服驱动逻辑架构。

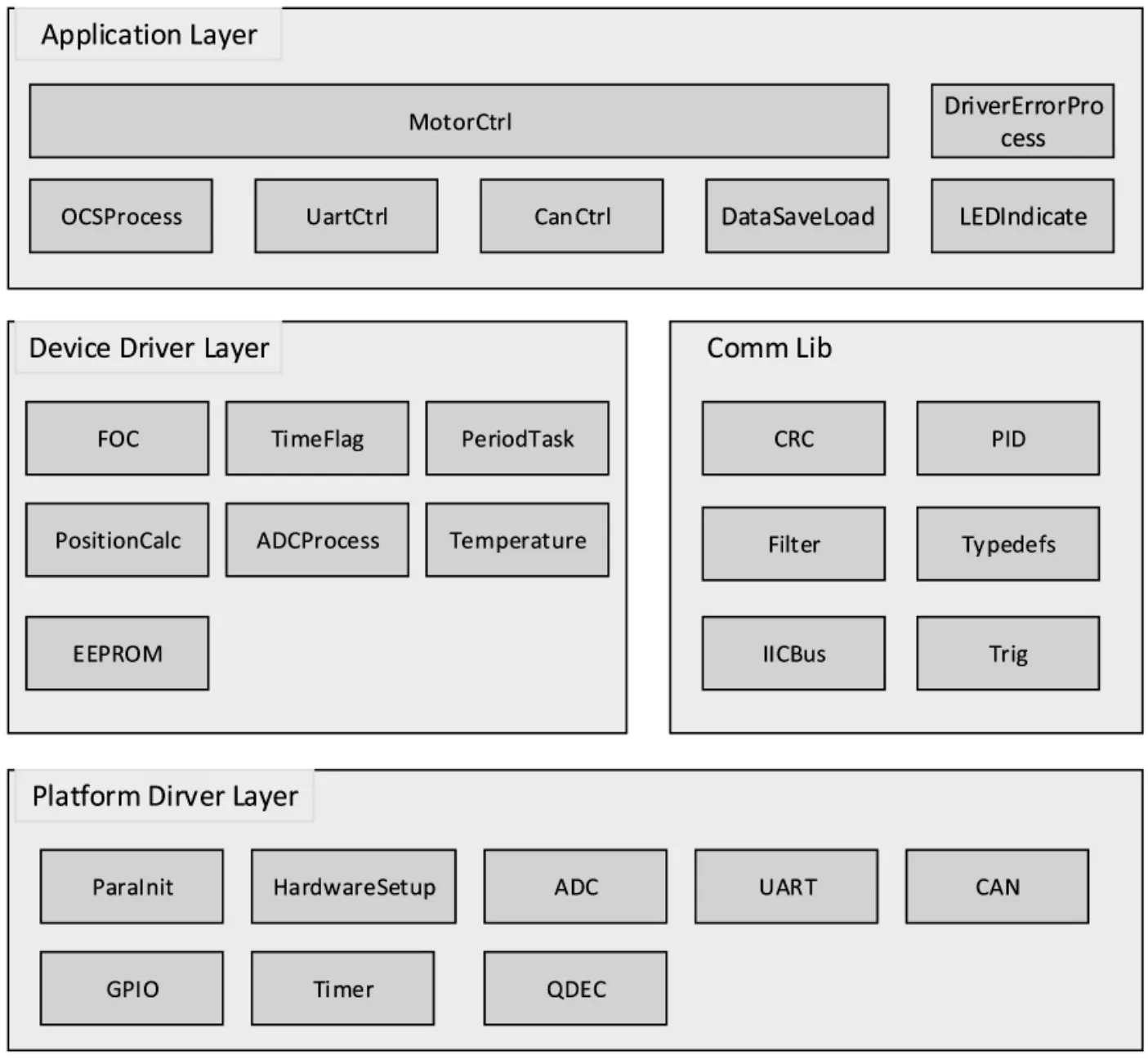
图6 伺服驱动逻辑架构Figure 6 Servo drive logic architecture

2.2 模块对应关系

功能模块关系如图7 所示， 主要分为四条线路。

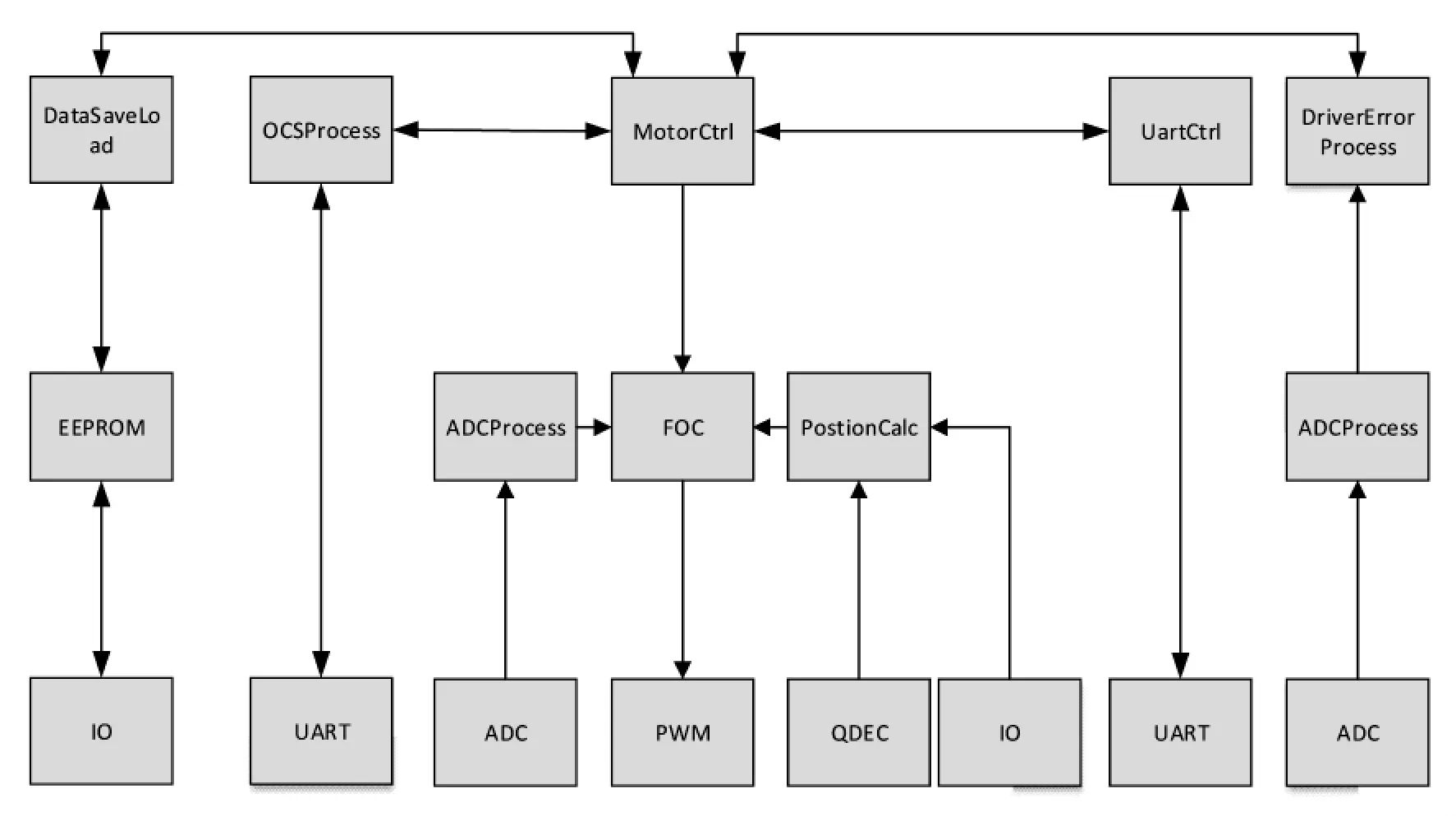
图7 伺服驱动功能模块关联图Figure 7 Servo drive function module correlation diagram

第一， 存储线路： 主要需要用到EEPROM 和DataSaveLoad 等模块，电机控制通过这些模块对数据进行读取和存储。

第二，模数转换线路：对传输进来的数据量进行模数转换，并进行驱动控制。

第三， 通讯线路： 主要通过CAN 通讯、UART通讯等对上位机，电机等设备进行数据传输和指令接发。

第四，控制线路：电机控制模块通过各种信息进行S 曲线生成、路径规划和FOC 控制等。

3 控制算法设计

3.1 控制框架

伺服控制系统如图8 所示， 包括坐标变换、SVPWM 空间矢量算法、三闭环控制技术、S 曲线运动控制算法和前馈控制算法等。 首先，通过S 曲线运动控制算法计算出位置信息；然后将给定的位置信息和编码器采集到的位置信息的差值，输入到位置环中，形成位置闭环反馈控制；再将给定速度值和反馈速度的差值送入速度环中，速度环的输出结果会通过电流环计算出d 轴q 轴电流。 最后，再通过坐标变换、SVPWM 空间矢量完成对电机的输出。其中在速度环和电流环中加入了由S 曲线规划产生的速度和加速度信息，用于前馈控制，从而提高各个环的精度和响应速度。

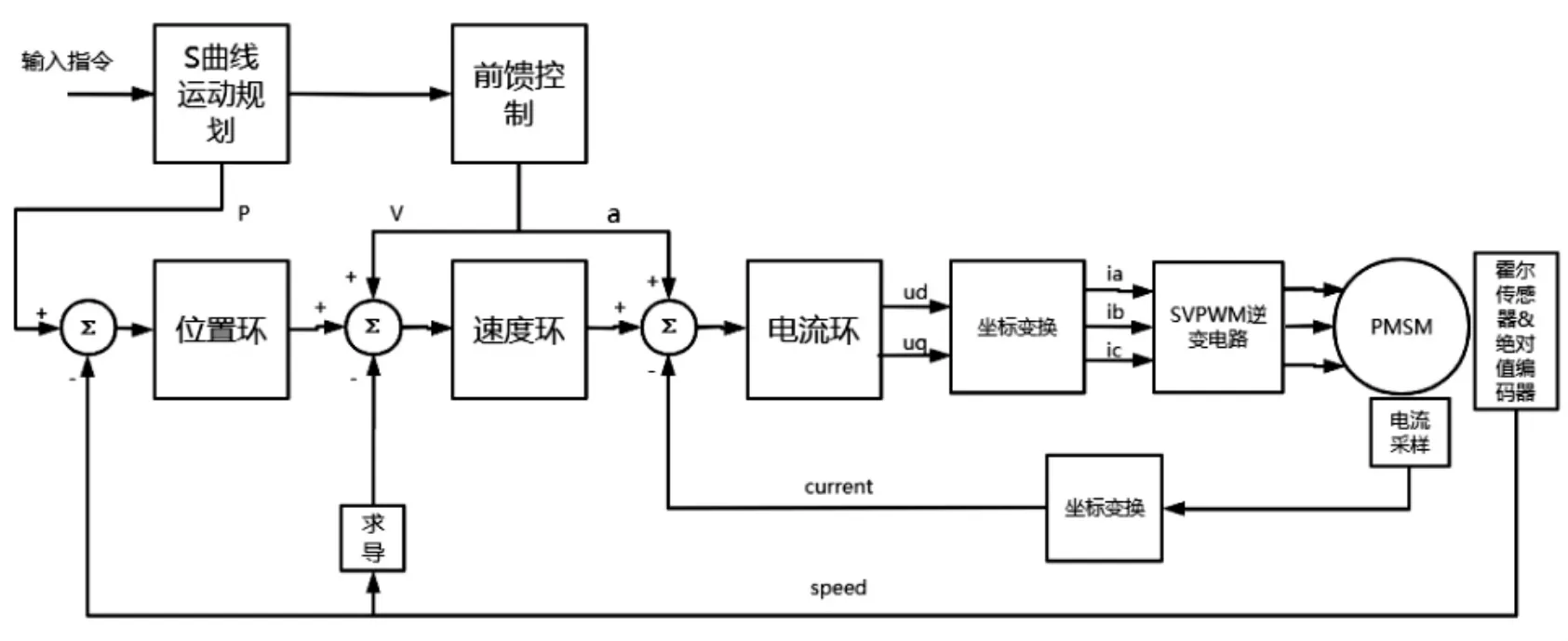
图8 伺服驱动软件平台架构Figure 8 Servo drive software platform architecture

3.2 S 曲线控制

伺服电机在启动和停止阶段分别会出现加速和减速的过渡过程，加入S 曲线可以保证伺服系统平稳运动，避免冲击和振荡。 在伺服控制中，S 曲线具有启动时需要伺服电机输出转矩小，加减速时高次谐波分量少，速度平滑性较好等优点，本项目中加减速运行过程可分为3 段：加速段（T1）、匀速段（T2）、减速段（T3），S 曲线加减速过程中位置、速度、加速度、加加速度变化情况如图9 所示。

图9 S 曲线示意图Figure 9 Schematic diagram of S curve

本系统中加加速度使用正弦函数来代替正负函数，这样的目的是可以合并加加速阶段和减加速阶段，合并加减速阶段和减减速阶段，计算加速度、速度和位置时更简便。 另外，本系统中的S 曲线考虑了在有初始速度情况下的运动规划，解决在有速度时接受位置指令后的规划问题。

S 曲线加减速过程中位置s、 速度v、 加速度a、加加速度j在三个阶段的值分别为：（初始速度为v0）

加速阶段（T1），t∈[0，T1]：

匀速阶段（T2），t∈[T1，T2]：

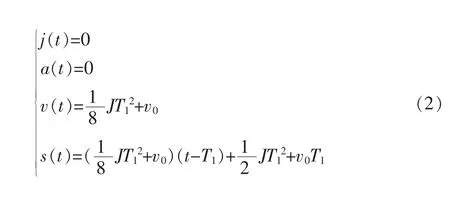
减速阶段（T3），t∈[T2，T3]：

3.3 前馈优化

在伺服系统中，前馈控制可以用来提高系统的响应特性和跟踪性能，前馈控制的特点是无须等到被控变量出现偏差，而是直接按照预先给定的指令给出控制量[5]。

传统前馈控制如图10 所示，其中G（s）是PID控制器与系统结合的传递函数，R（s）是系统输入量，Y（s）是系统输出。N（s）就是前馈控制的传递函数。

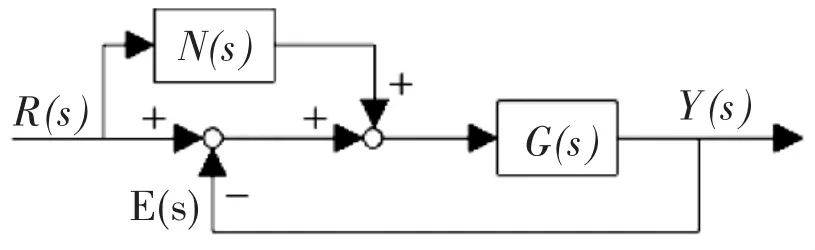
图10 前馈控制示意图Figure 10 Schematic diagram of feedforward control

由图可得，前馈控制系统的系统输出Y（s）等于：

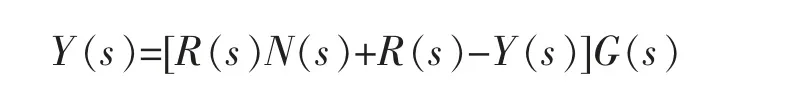
可得：

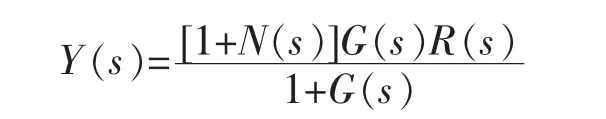
我们期望的理想系统，就是输出量可以准确、快速地跟随系统输入量，所以理想情况下Y（s）=R（s）。 由此可得N（s）=1/G（s）

所以对于系统而言，当N（s）=1/G（s）时可以实现输出量对输入量的完全跟随，达到理想的前馈控制。 但在实际的情况中由于系统比较复杂，一般采用部分补偿的方式对系统进行补偿。

由于普通的前馈补偿需要将输入的位置信息再进行两次微分， 实现对速度和加速度信号的补偿，但微分会导致系统计算时间上升和复杂度。 在本系统中， 我们采用将S 曲线规划中计算得到的速度和加速度信息直接按一定比例补偿给速度环和电流环，实现更简便的前馈补偿，具体原理如图11 所示。

图11 S 曲线输出优化前馈控制示意图Figure 11 Schematic diagram of S-curve output optimized feedforward control

对于速度环和电流环来说，对应的输入除上一环解算的数据外还要加上S 曲线计算出的速度或加速度。 公式如式（4）和式（5）所示：

式中：Vref——速度环的输入参考速度；

pidpos——位置环的输出结果；

vsref——S 曲线计算出的速度值；

cofv——速度值的系数；

iqref——电流环的输入参考速度；

pidvel——速度环的输出结果；

asref——S 曲线计算出的加速度值；

cofa——加速度值的系数。

4 试验结果分析

4.1 试验环境搭建

本文设计的伺服驱动器所使用的电机采用maxon 公司的EC90flat 型号电机，电机的主要参数为额定电压24V， 额定电流0.658A， 额定转速3179rpm，每相电阻0.216Ω。 每相电感0.232mh，极对数11，转矩系数71.2nNm/A，转动惯量3170gcm2。

本文主要验证在旋转一定角度情况下伺服驱动器的控制效果。

4.2 结果对比

本试验分别对比了之前S 曲线输出和分别加入速度前馈、 加入速度和加速度前馈情况下的位置输出曲线。 图12 为原始S 曲线输出示意图，图13 为加入速度前馈后S 曲线输出示意图，图14 为加入加速度和速度前馈后S 曲线输出示意图。 其中灰色线代表电机参考位置， 黑色线代表电机实际转动位置。

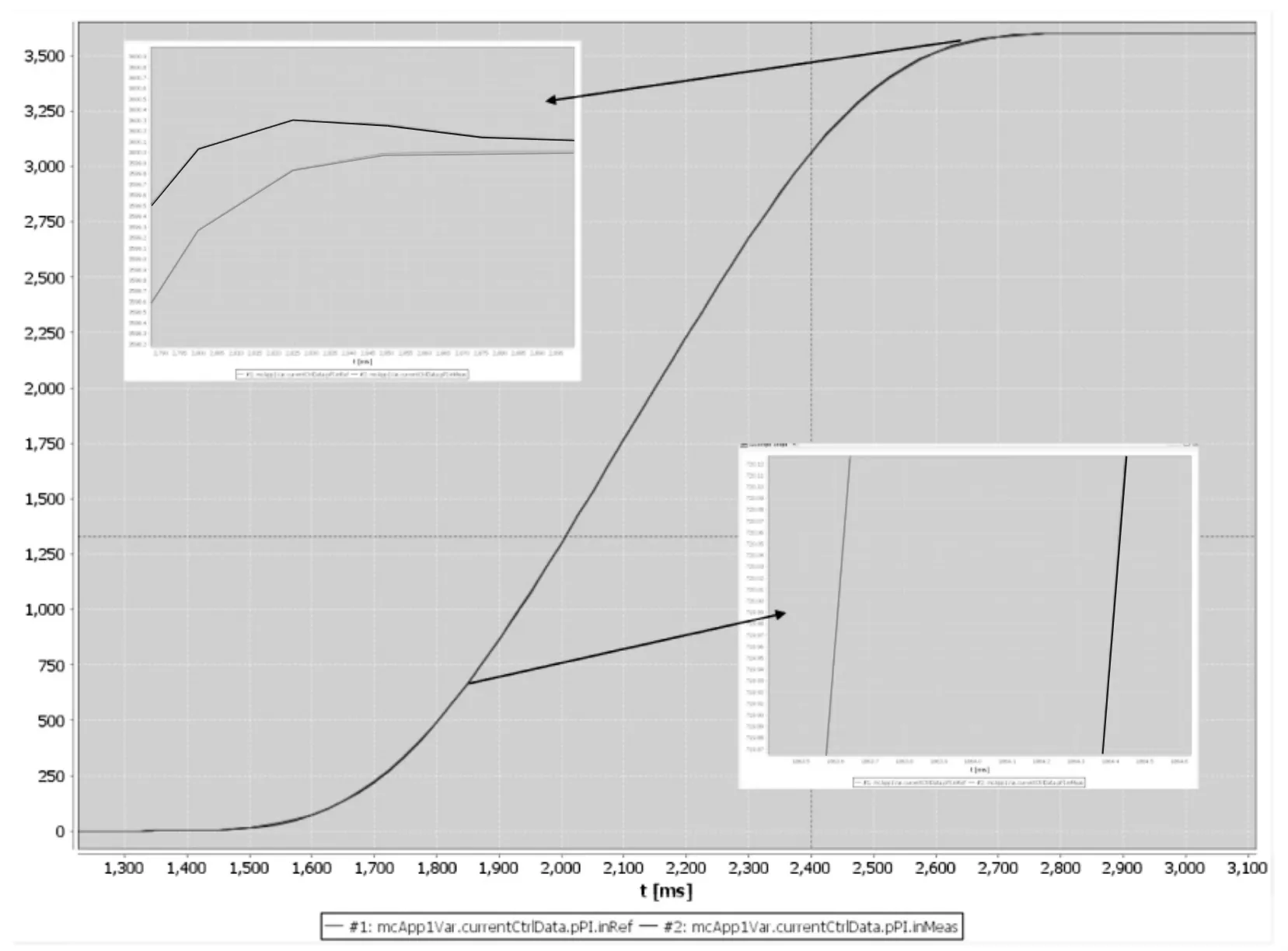
图12 原始S 曲线输出示意图Figure 12 Schematic diagram of the original S-curve output

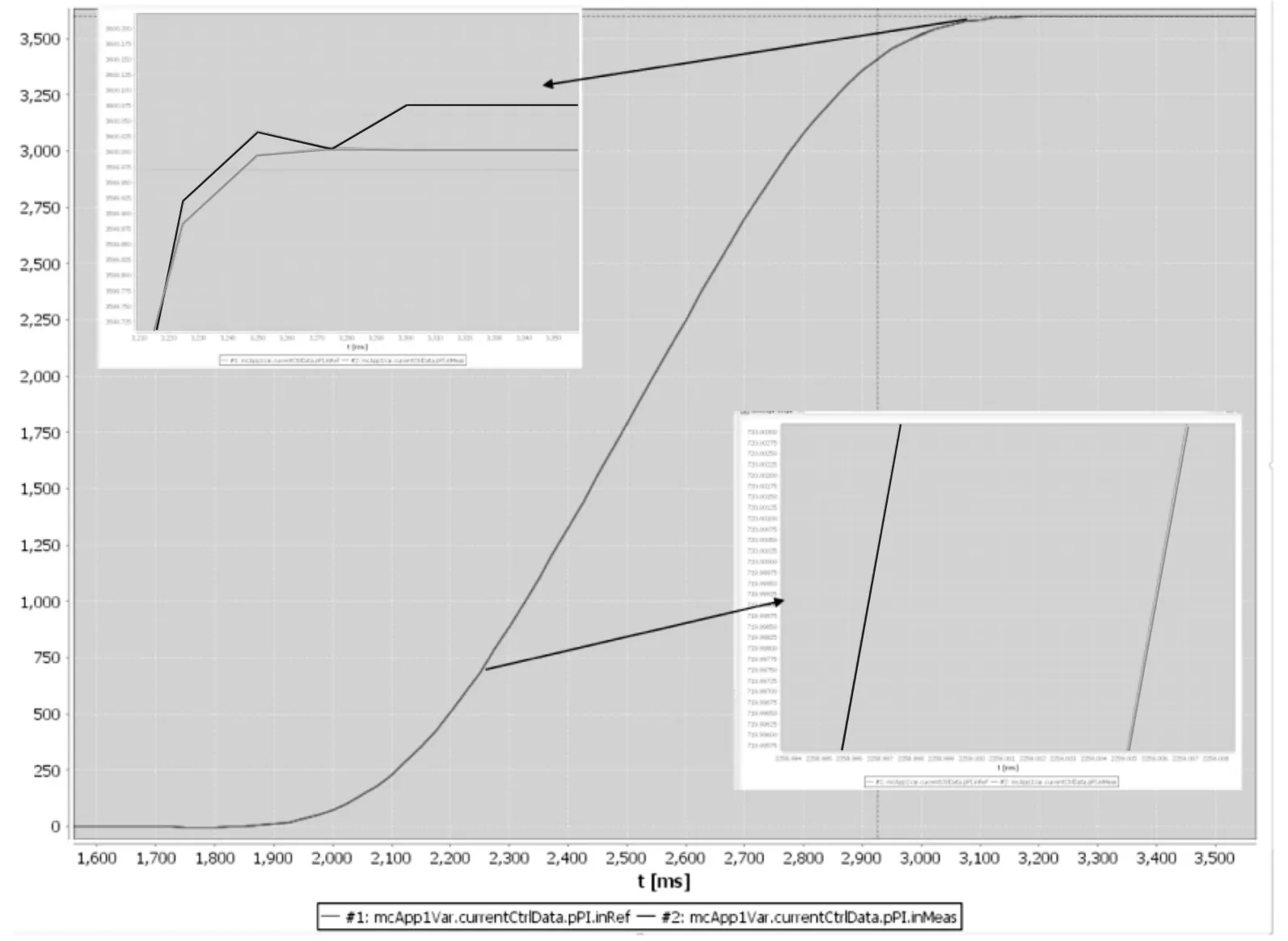
图13 加入速度前馈后S 曲线输出示意图Figure 13 Schematic diagram of S-curve output after speed feedforward is added

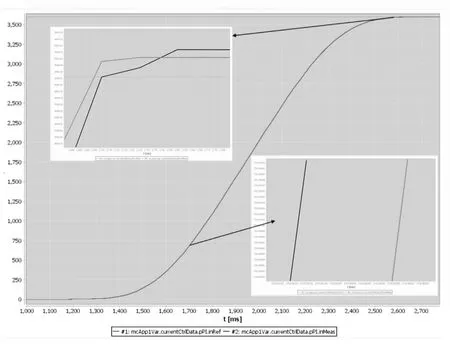
图14 加入加速度和速度前馈后S 曲线输出示意图Figure 14 Schematic diagram of S-curve output after acceleration and velocity feedforward are added

在为伺服驱动器供电后， 控制位置环由0°旋转到3600°， 图12、13、14 分别为三种情况下的S曲线输出。 比较三者曲线可以得出，采用普通S 曲线控制时，超调量为0.3°，稳定时的误差为0.146°，采用速度前馈时超调量为和稳定时的误差均为0.0766°， 采用速度和加速度前馈时超调量和稳定时的误差为0.01416°。另外通过对比启动后旋转到720°时的曲线， 我们可以得出三种方法的跟随效果：采用单S 曲线时，到达720°的目标和实际曲线误差在0.8ms；而加入速度前馈后为0.093ms，加入速度和加速度前馈后为0.0003ms。 由试验可以看出，在加入速度前馈后，超调减少74.5%；稳态误差减少47.5%，跟随时间减少88.4%；另外加入加速度前馈后，超调减少95.2%，稳态误差减少90.3%，减少了99%的跟随时间，提高了电机的响应速度。

5 结语

本文设计了基于S 曲线的前馈三闭环PID 控制低压伺服驱动器，采用了ARM7 内核芯片，具有低电压大功率、运算速度快、控制精度高等特点。通过电机驱动电路实现整体的回路控制功能，反馈电路支持相对编码器和霍尔传感器，并有SWD，USB，CAN，RS232 等多种通讯方式； 通过电流读取和温度传感器等实现过流保护、温度保护等功能。 伺服驱动器软件分为应用层、设备驱动层、平台驱动层和通用库四大模块，通过各个模块之间的通讯和调用实现存储、模数转换、通讯、控制等功能。

本文在使用S 曲线平稳运动的基础上，在速度环和电流环中加入S 曲线计算生成的速度和加速度作为前馈补偿。 试验证明，加入前馈补偿有效提高了电机实际的跟随性能，同时电机超调和精度也有所提高。 与单独在速度环加入前馈补偿相比，速度环和电流环都加入前馈补偿在超调量、 稳态误差、跟随效果上都有更好的表现。 该驱动器与传统前馈控制相比，无需进行微分计算，减少了计算量，具有较大的应用价值。