空间调制系统中一种低复杂度比特映射算法

李贵勇，郑开放，陈 洋，孙星陪

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引 言

在空间调制系统中[1]，发送的比特块被分为2部分，即天线选择比特和调制比特。虽然天线选择比特在每个传输时隙激活指定的发射天线，但是调制比特是实际调制和发送的那部分比特。由于空间调制(spatial modulation,SM)在每个传输时隙仅激活单个发射天线，因此，SM可以避免信道间干扰和降低接收端的复杂性，并在发射端采用单个射频链路，降低了设备成本[2-3]。

比特映射是将比特序列分配给不同符号的过程，比特映射的选择会影响任何调制方案的误码率(bit error rate,BER)性能[4]。在传统幅度相位调制(amplitude-phase modulation,APM)过程中，用于比特映射的方法是格雷编码，在同等可能和统计独立APM符号情况下被证明是最优的。在格雷编码中，相邻的符号被分配的比特序列仅有1 bit不同。SM与APM方案不同，由于其混合特性，SM的比特映射更具有挑战性，其中使用APM和空间来创建更为复杂的星座结构。因此，在SM系统中，针对APM方案提出的经典格雷映射将不在实现最优的BER性能。

文献[5-8]提出了几种有效的比特映射方案。在文献[5]中，假设在发射端使用全信道状态信息(channel state information,CSI)，作者针对SSK系统提出一种比特映射算法，称为原始二进制切换算法(original binary switch algorithm,OBSA)，该算法最初以自然比特映射为SM符号分配比特序列，然后对于每2个符号的组合，该算法切换分配给这2个符号的比特序列，在每次切换时，计算比特映射的BER，然后选择具有最佳性能的比特映射。该算法在高BER情况下，其系统性能接近于BER的下界。然而，OBSA 算法的主要问题是计算复杂度较高，计算复杂度为O(K4)，其中K是符号数。在文献[6]中，假设发射端的CSI已知，作者提出了一种应用于SM的比特映射方案。该方案将格雷编码应用于APM部分，在空间部分采用随机比特映射。该方案仅在APM星座小于8时为系统性能提高了小于1 dB的改进。在文献[7]中，作者为SM系统提出一种比特映射器，称为暴力映射器(brute forth mapper,BFM)。BFM找到具有最小距离的2个SM符号，并为这2个符号分配仅有1比特不同的比特组合。对于剩余的SM符号，BFM在空间部分采用自然映射，在APM部分采用格雷编码。BFM在高信噪比(signal-to-noise ratio, SNR)情况下实现接近BER下限的性能，并且具有较低的计算复杂度为O(K2)和较低的反馈开销为2lbK，BFM算法的主要问题是在低SNR下几乎没有性能的改善。

在本文中，假设在发射端使用全信道状态信息，提出一种新颖的低复杂度比特映射方案，称为SNM算法。该方案首先以符号之间的距离最近为标准进行排序，然后对排序后的SM符号应用格雷编码。仿真结果表明，SNM算法在瑞利衰落信道环境中，其性能接近于OBSA算法，并且在高SNR情况时，其性能接近于SM和SSK的BER的下限。在复杂度方面，所提出的算法复杂度仅为O(K2)，显著低于OBSA算法。SNM算法的反馈开销为(K-1)lbK，略大于BFM算法。然而，SNM算法比BFM算法提供了更好的性能。

1 系统模型

对于具有SM传输的Nt×Nr的多输入多输出(multiple input multiple output, MIMO)系统，其中Nt和Nr分别是发射天线数和接收天线数。SM符号总数为K=MNt，其中M是APM大小。假设Nt和M都是2的整数幂，令k1=lbNt，k2=lbM，则k=k1+k2比特用于根据某个比特映射方案选择APM符号和一个发射天线，如图1。

图1 SM系统模型图Fig.1 SM system model

接收信号矢量y∈Nr×1表示为

(1)

(1)式中：H∈Nr×Nt是信道矩阵；ρ是信噪比；n∈Nr×1是噪声矢量，且n～CN(0,1)；x∈Nt×1是发射矢量，sm是第m个APM符号。

通过文献[2]可知，在接收端可以通过最大似然(maximum likelihood,ML)检测去估计接收到的信号，其估计值为

(2)

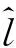
2 算法分析

在本节中，首先对本文需要解决的问题进行描述，给出比特映射的最优问题，如果采用穷举搜索去求解最优问题，给出了穷举搜索的搜索复杂度，由于穷举搜索的复杂度较高，给出了改进方向；接着提出了SNM算法，并对该算法进行了详细的描述，给出该算法的具体计算步骤；然后举例进一步地解释了所提出的算法；最后对复杂度进行了分析。

2.1 问题描述

在文献[8-9]中，给定确定的比特映射方案Γ的SM的BER上界，可以用Pe表示为

(3)

(3)式中：DΓ(k,k′)是给定的比特映射方案Γ的第k个SM符号和第k′个SM符号之间的汉明距离。P(k,k′)是第k个SM符号和第k′个SM符号之间的成对错误概率。

对于在发射端使用全CSI的情况，其成对错误概率P(k,k′)可以写为

(4)

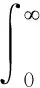
由以上的分析可知，比特映射最优化问题可以描述为

(5)

(5)式中：Γout是最优的比特映射。定义d∈K×K是对称矩阵，矩阵d中的各项是距离度量。

可以通过穷举搜索所有可能的比特映射来寻找最优的比特映射Γout，但是采用穷举搜索是极其复杂的。对具有K个SM符号进行穷举搜索，需要穷举搜索所有可能，一共有K!种。即使K很小时，其搜索复杂度也较高，例如当K=8时，需要进行8!=40 320次搜索才可以得到最优的比特映射Γout。

由以上的介绍可知，针对穷举搜索复杂度较高的问题，需要一个合适的方案去求得最优的比特映射 Γout。在空间调制系统中，距离最近的符号较容易出现误判的比特，但如果这2个符号所对应的比特之间的汉明距离越小，则在出现误判时，出错的比特数就越小。所以在判决准确率一定的情况下，使得相邻星座点之间汉明距离较小的映射方案，将获得较优的BER性能。

因此，本文给出的改进方向是通过以SM符号之间的距离为标准对SM符号进行排序，由于格雷编码相邻比特序列的汉明距离为1，于是将格雷编码的比特序列分配给已排序的SM符号。

2.2 SNM算法

设w=[1,2,3,…,K]代表一共有K个SM符号，v∈1×K用来存储排序后的SM符号，定义是第k个SM符号和第k′个SM符号之间的距离度量，定义d∈K×K，矩阵d中的各项是距离度量。

为便于对SM符号进行排序，令相同SM符号之间的距离度量为无穷大，具体SM符号之间的距离度量计算表达式为

d(k,k′)=d(k′,k)=

(6)

在SNM算法的第1步中，是将SM符号进行排序，排序流程如图2。

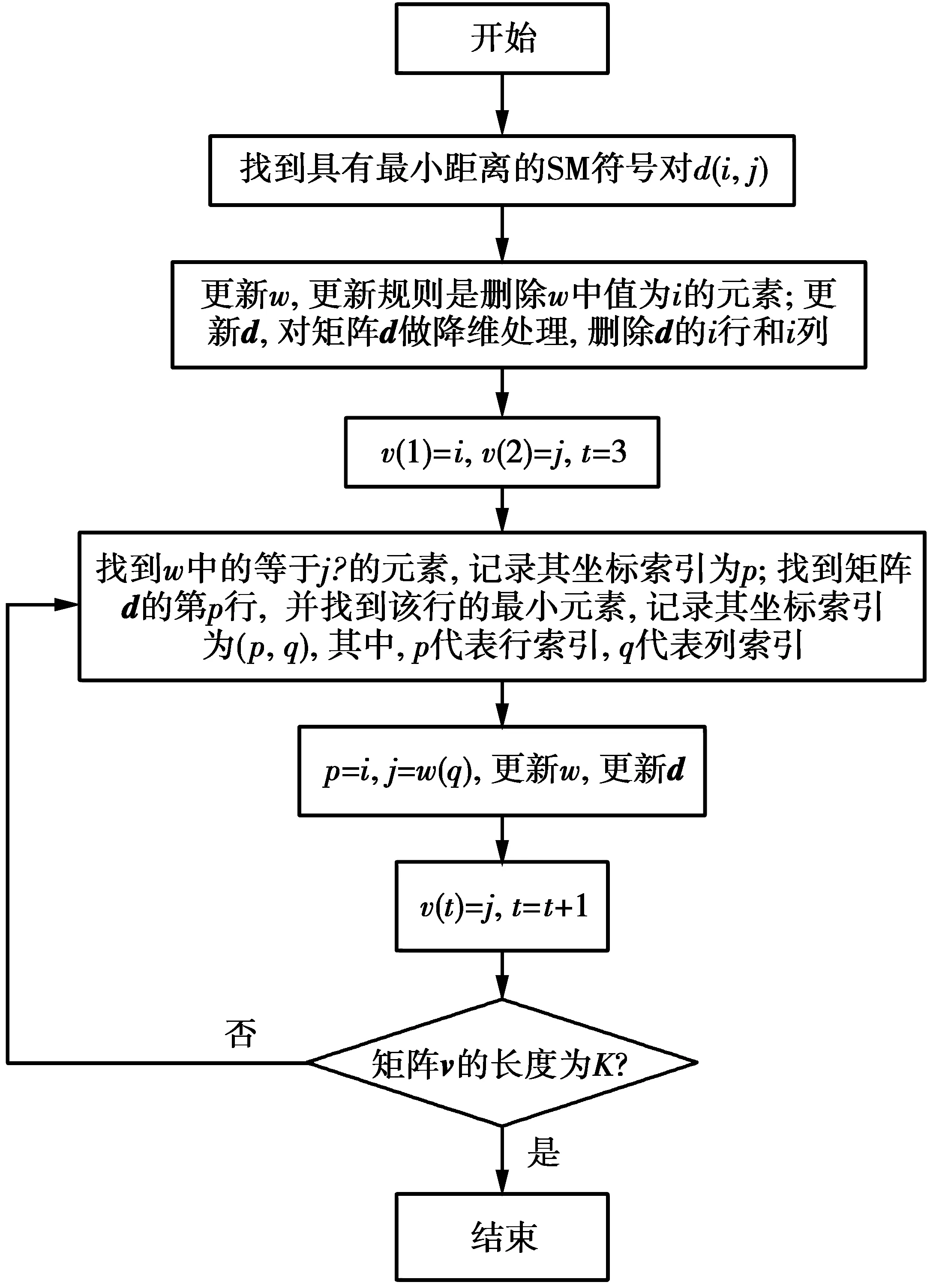
图2 SM符号排序流程图Fig.2 SM symbol sorting flow diagram

在SNM的第2步中，是将格雷编码的比特映射分配给前一步骤中已排列次序的SM符号。

以上给出了SNM算法的排序流程图，且给出了w和d的更新规则，该算法具体计算步骤总结如下。

SNM算法

输入：信道矩阵H，S={s1,s2,s3,…,sM}

输出：ΓSNM

初始化：d是维度为K×K的矩阵，且初始化所有元素均为0；初始化v为空矩阵；w=[1,2,3,……，K]

1 fork=1∶K

2 fork′=1∶K

3 ifk=k′

4d(k,k′)=∞

5 else

6 计算d(k,k′)

7d(k′,k)=d(k,k′)

8 end if

9 end for

10 end for

11 从矩阵d中寻找最小的元素d(i,j)

12 更新w，更新d

13 令v(1)=i，v(2)=j，t=3

14N=length(w)

15 whileN==Kdo

16p=矩阵w中等于j的元素的索引

17y=d(p,:)

18q=y中最小元素的索引

19i=p，q=w(j)，更新w，更新d

20v(t)=j

21t=t+1

22N=length(w)

23 end while

2.3 算法举例

假设K=4，即有4个SM符号，且具有以下任意距离矩阵为

(7)

其排序过程如图3，其中w记录矩阵降维处理后剩余的SM符号；v存储已排序的SM符号。

由以上的排序过程可知，SM符号的排序结果为v=[1,2,4,3]。

排序结束后将格雷编码的比特映射按次序分配给SM符号，即将00分配给SM符号#1，01分配给SM符号#3，11分配给SM符号#4，10分配给SM符号#2。

2.4 复杂度分析

2.4.1OBSA算法

对于OBSA算法，在文献[5]中表明，由实数乘法和实数求和以及比较次数复杂度可以表示为

(8)

(9)

(10)

图3 SM符号排序过程图Fig.3 SM symbol sorting process diagram

2.4.2SNM算法

在该算法中，需要计算K(K-1)/2个距离度量，还应计算smhl，一共计算K次，计算并储存该结果。在初始时应寻找距离矩阵d的最小元素，需要经过K2次比较，然后确定2个SM符号的排列顺序；在对剩余的K-2个SM符号排序过程中，确定第ε个符号需要经过K-ε+2次比较，其中ε=[3,4,…,K]。对于每个距离度量的计算，需要2Nr次实数乘法和4Nr-1次实数求和；计算smhl，需要4Nr次实数乘法和2Nr次实数求和。

由以上分析可知，实数乘法、实数求和以及比较次数复杂度可以表示为

(11)

(12)

(13)

在实际工程中，接收天线数Nr一般设置为2或4，而K在实际工程中一般设置为2β，且β∈{5,6,7,8,9,10}。

因此，在实际中K远大于Nr，则SNM算法的复杂度为O(K2)。因此，该算法的计算复杂度比OBSA算法低得多，OBSA算法的复杂度为O(K4)。并且SNM算法的系统性能接近于OBSA算法。

2.4.3 反馈开销

SNM算法通过发送已排序的K-1个SM符号的索引反馈给发射端，之所以只发送K-1个SM符号的索引，是因为当K-1个SM符号的索引确定后，第K个SM符号的索引也即确定。由于每个SM符号对应lbKbit，所以SNM算法需要(K-1)lbKbit用于反馈。

由以上分析可知，SNM算法的反馈开销为(K-1)lbKbit ，与BFM算法2lbKbit的反馈开销相比，SNM算法能提供更好的系统性能来弥补这一点。另一方面，与OBSA算法2lbK!比特的反馈开销相比，SNM算法具有较低的反馈开销。

2.5 性能界限

设Ps是符号错误率，k=lbK代表每个SM符号的比特数。最低的BER是Ps/k(每个符号SM错误仅有1 bit误码)。因此，误码率的下界可以表示为

(14)

(15)

然而，(14)式的下界与Γc性能的差值可以用dB的形式表示为[10]

(16)

(17)

将(16)式作为比特映射方案性能增益的上界，良好的比特映射方案将有接近此界限的性能改进。

3 仿真分析

本文对所提出的算法进行了详细的介绍，为了更为直观的展示SNM算法的性能，对SNM算法进行仿真以验证其性能，具体的仿真参数见表1。

表1 具体仿真参数设定

为了证明本文提出的SNM算法的性能，本节给出了Γc的BER性能，以验证SNM算法给系统性能带来的提升。同时，对BFM算法、OBSA算法、BER下界进行仿真，以进一步验证SNM算法的性能。

图4是Nt=8，Nr=2时不同信噪比下SM系统的BER性能，图5是Nt=16，Nr=2时不同信噪比下SSK系统的BER性能。

图4 在SM系统中，SNM算法的BER性能(Nt=8,Nr=2)Fig.4 BER performance of the SNM algorithm in the SM system (Nt=8, Nr=2)

从图4、图5可以看出，与BER性能的上界Γc相比，SNM算法可以显著提高系统性能，例如在SNR=16 dB时，图4中采用16QAM时，系统性能提高约3.1 dB，采用4QAM时，系统性能提高约3.4 dB；图5中采用16QAM时，系统性能提高约3.3 dB，采用4QAM时，系统性能提高约3.7 dB。与BFM算法相比，SNM算法也可以显著的提高系统性能，例如在SNR=10 dB时，图4中采用16QAM时，系统性能提高约1.5 dB，采用4QAM时，系统性能提高约1.8 dB；图5中采用16QAM时，系统性能提高约1.8 dB，采用4QAM时，系统性能提高约1.9 dB。虽然SNM算法的反馈开销大于BFM算法，但SNM算法提供了较好的系统性能。与OBSA算法相比，SNM算法不仅其系统性能与OBSA算法相当，并且其复杂度也较低。与BER的下界相比，在高SNR情况下，SNM算法的系统性能接近于BER下界。

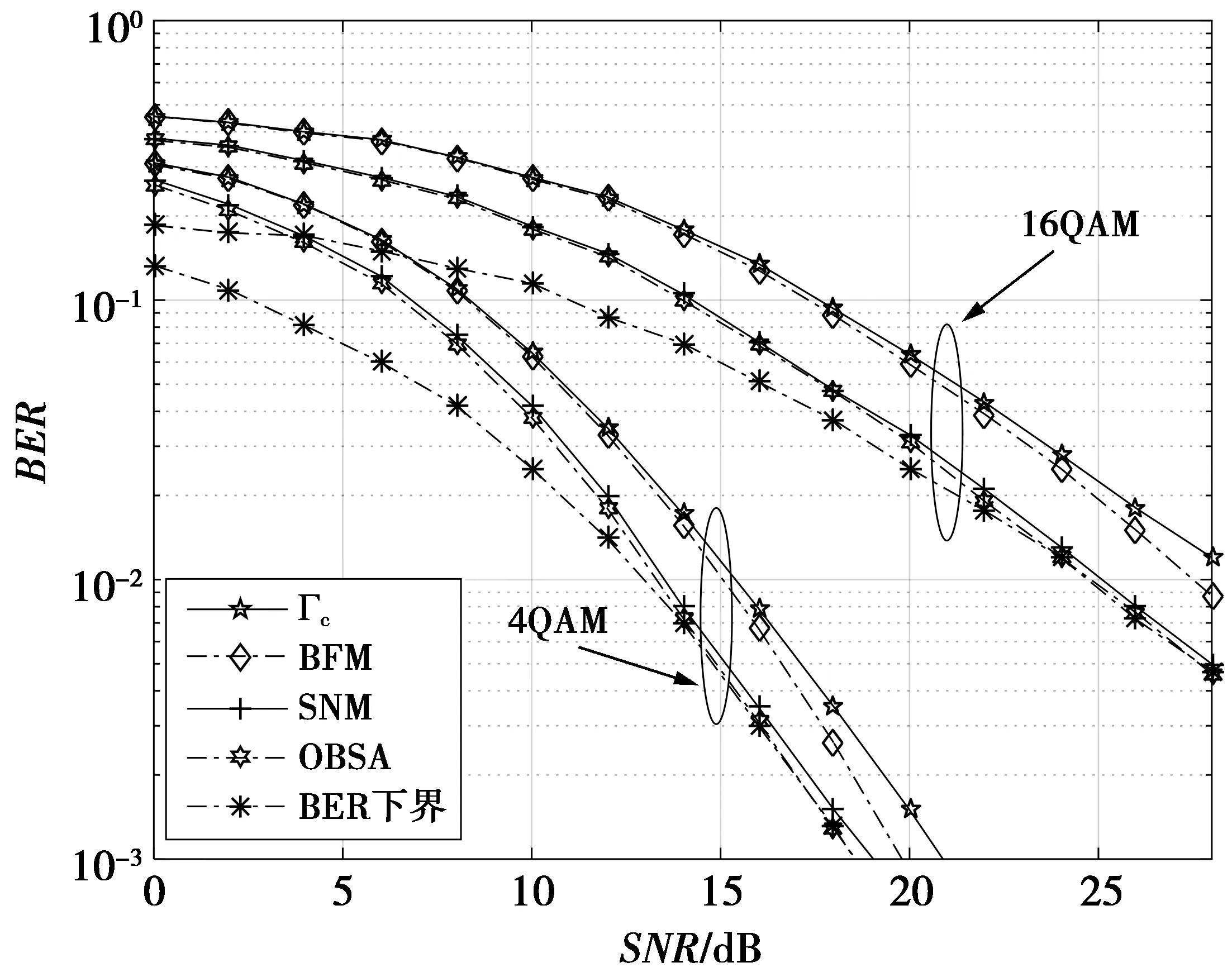
图5 在SSK系统中，SNM算法的BER性能(Nt=16,Nr=2)Fig.5 BER performance of the SNM algorithm in the SSK system (Nt=16, Nr=2)

通过对以上仿真结果的分析得出，SNM算法可以显著提高系统性能，SNM算法的复杂度比BFM算法高，但其系统性能远优于BFM算法；SNM算法在具有较低复杂度的情况下其系统性能与OBSA算法相当，之所以SNM算法与OBSA算法的系统性能相当，是由于本文提出的算法与OBSA算法均是通过搜索去确定最优的比特映射 Γout；SNM算法在高SNR情况下，系统性能接近于BER下界。

4 结 论

本文针对SM系统的比特到符号映射方案提出了SNM算法。该算法通过从具有最小距离的符号对开始对SM符号进行排序，接着继续对最近的SM符号排序，直到所有的SM符号排序结束为止。接着将格雷编码的比特映射按顺序分配给已排序的SM符号。仿真结果表明，SNM算法在发射端使用全信道状态信息时，其系统性能接近于SM和SSK算法的BER的下界。