薛定谔、KdV、KdV-Burgers方程的椭圆函数解和孤立子
——非线性偏微分方程的解
2021-03-11 11:20:24肖婷婷
陇东学院学报 2021年2期
肖 婷 婷
(陇东学院 数学与统计学院,甘肃 庆阳 745000)
1 薛定谔方程
定态的薛定谔方程为
其中U是势函数,ħ是常量,μ是粒子质量。
1.1 1维薛定谔方程
1维的薛定谔方程为
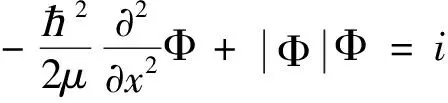
(1)设Φ=Φ(x,t)=φ(x)e-ilt,其中φ(x)=JacobiSN(x,λ)2+B,这里B和l是待定的系数,λ是参数(0≤λ≤1)。代入上述方程,经过整理和合并同类项,得到一个只关于函数JacobiSN(x,λ)的方程。再令每一项的系数为零,得到关于参数B,l,μ,λ的方程,解这个方程组得到对应参数的值。
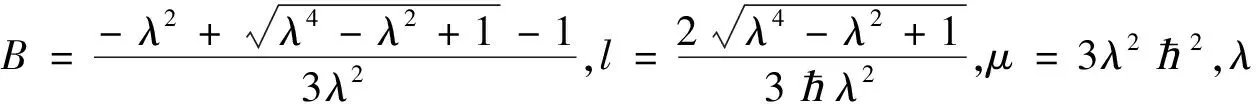
解Φ1(x,t)=
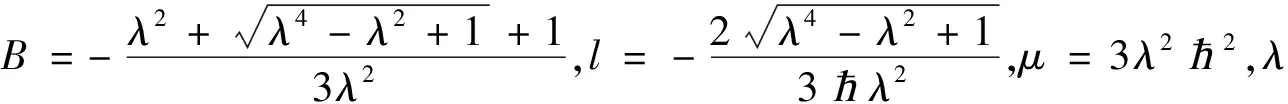
解Φ2(x,t)=
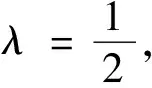
为了求出孤子解设φ(x)=tanh(k1x)2+B。得到如下的参数值和解:
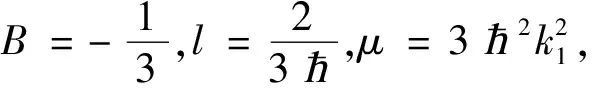
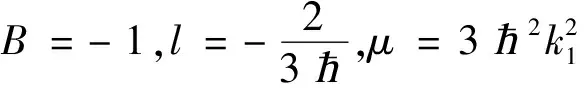

设φ(x)=tanh(x)2+B。
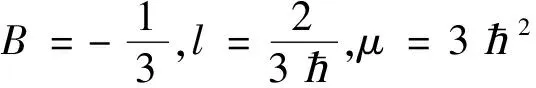
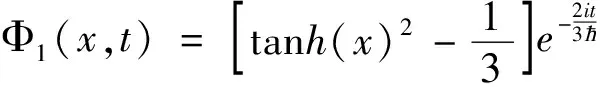
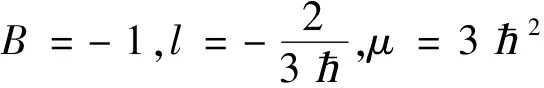
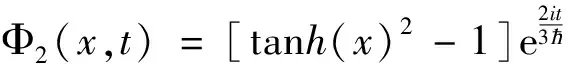
(2)设Φ=Φ(x,t)=φ(x,t)e-i(kx+lt),其中φ(x,t)=JacobiSN(x+lt,λ)2+B。得到
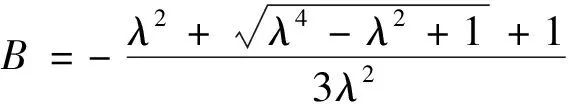
解Φ1,2(x,t)=
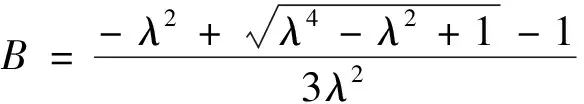
解Φ3,4(x,t)=
解Φ1,2(x,t)=
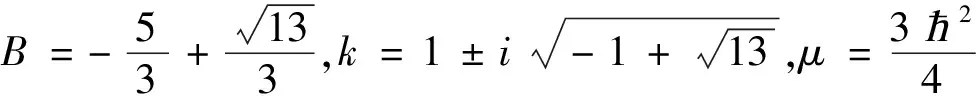
解Φ3,4(x,t)=
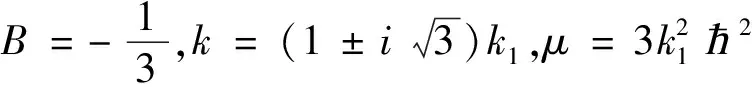
解Φ1,2(x,t)=
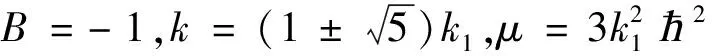
解Φ3,4(x,t)=
1.2 3维薛定谔方程
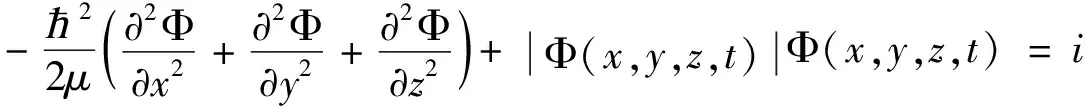
(1)设Φ=[Atanh(x+y+z)2-1]e-ilt。
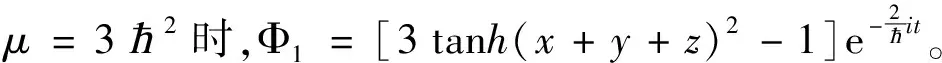
(2)设Φ=[Atanh(x+y+z+wt)2-1]e-i[k(x+y+z)+lt]
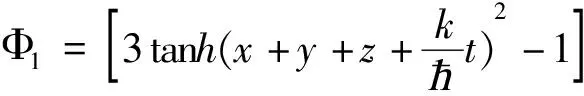
2 KdV、KdV-Burgers方程
2.1 标准KdV方程
标准KdV方程
是1895年由荷兰数学家科特韦格和德弗里斯共同发现的一种偏微分方程,有钟形、扭形、暗孤波解。
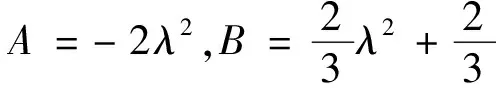
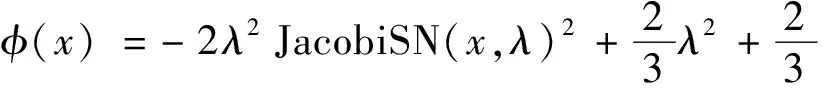
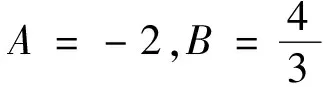
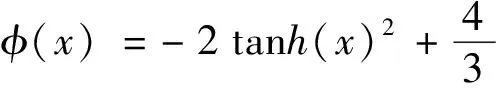
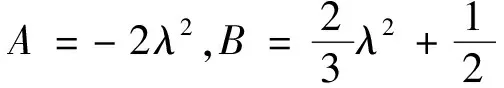
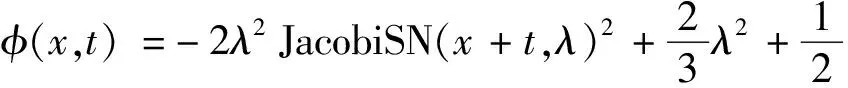
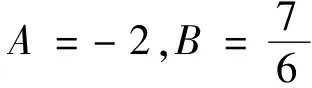
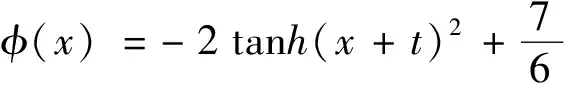
2.2 KdV-Burgers方程
KdV-Burgers方程为
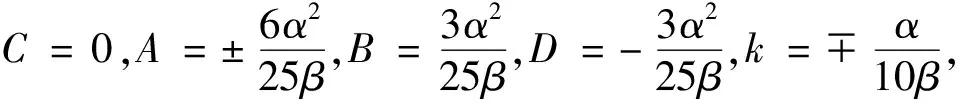
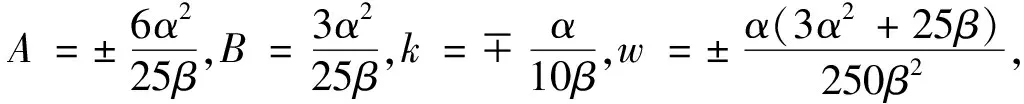
总结:最近的研究也在不断改进反演散射方法、Bäcklund变换、Darboux变换。
猜你喜欢
数学物理学报(2022年3期)2022-05-25 13:33:26
数学物理学报(2022年1期)2022-03-16 06:15:04
数学物理学报(2021年6期)2021-12-21 06:24:22
数学物理学报(2020年1期)2020-04-21 06:00:56
数学物理学报(2019年1期)2019-03-21 05:26:28
数学物理学报(2018年6期)2019-01-28 08:58:08
幽默大师(2019年6期)2019-01-14 10:38:13
数学物理学报(2018年1期)2018-03-26 08:16:51
新乡学院学报(2016年6期)2016-12-01 05:21:38
厦门理工学院学报(2016年1期)2016-12-01 04:50:52

