基于Chen超混沌系统的改进AES算法的实现

刘海峰 邹丹阳

（陕西科技大学 陕西省西安市 710021）

随着信息技术的不断发展，对传统加密体制的安全性能要求也在提高。传统的AES 算法的S 盒具有迭代周期较短的特点，严重地影响了S 盒的安全性[1]。同时，密钥扩展算法存在缺陷：轮密钥与种子密钥之间的关联性很强，一旦截取任意一轮子密钥，就可以通过已知的扩展算法计算出所有加密密钥，算法的安全性无法得到保障[2]。为了提高AES 算法的安全性能，现针对上述两个缺陷进行如下改进：采用新的仿射变换对来改进S 盒，同时基于流密码的特点，改进AES 算法的密钥扩展过程。

混沌系统由于具有对初始值敏感、内随机性及无周期性等特点，天然地与密码加密体制联系起来。欧成园等采用两种超混沌系生成混沌加密序列，产生的第一组序列与明文进行异或后，再使用第二组序列与用户密钥进行异或作为AES 加密的初始密钥，显著的扩大了加密密钥空间[3]。王勇等人通过与神经网络结合的方式，产生的超混沌序列作于图像加密的种子密钥进行AES 加密[4]。已有的通过混沌系统与加密算法的结合，常采用混沌映射对图像进行一定的扩散处理，或是使用混沌映射产生的序列作为AES 加密的种子密钥，未能充分利用混沌序列具有的良好随机性特点。本文使用超分数阶Chen 超混沌系统产生一种通过NIST 测试的可证明随机的序列作为密钥流，利用该密钥流采用类似一次一密加密的方式替代原始的密钥扩展过程，由于密钥流是均匀分布的离散无记忆随机序列，使得算法更难被破译，提高了算法的安全性。

1 S盒改进

AES 中S 盒的运算使用字节代替变换来完成对状态字节的非线性变换，该设计能够有效的针对明文与密文之间的联系进行混淆，但是经过分析发现传统的S 盒选择的仿射变换周期为4，最大迭代输出周期为87，存在短周期现象，容易受到差分攻击，并且计算其严格雪崩距离为432，不满足严格雪崩标准。因此，文献[5]提出了一种代数性质良好的仿射变换对，本文选择仿射变换对(D3,35)来进行新S 盒的构造，该放射变换对的严格雪崩距离为304，最大迭代输出周期为256，仿射变换周期为16。

得到的S 盒为查找替换表如表1所示。

表1：S 盒查找替换表

新的S 盒按照如下的方式进行构造：

（1）按照字节升序逐行初始化S 盒；

（2）把S 盒中的每个字节映射为它在有限域GF(28)中的逆；

（3）把S 盒中的每个字节的8 个构成为记为{b7, b6, b5, b4, b3,b1, b0}，对S 盒的每个字节逐位做以下变换：

bi'=bi⊕b(i+1)⊕b(i+2)⊕b(i+4)⊕b(i+7)⊕ci

这里的ci指的是值为{35}字节的第i 位，即{c7c6c5c4c3c2c1c0}=(00110101)2。

2 伪随机序列生成

2.1 分数阶Chen超混沌系统

分数阶Chen 超混沌系统[6]作为一种典型的混沌动力学系统，系统公式如下：

上述公式中，a，b，c，d，r 为系统参数，当a=35，b=7，此2，d=3，r 取值范围在[0.085,0.789]时，系统处于混沌状态，并存在4 个混沌序列X，Y，Z，W。与普通的混沌系统相比较，分数阶Chen 超混沌系统具有两个正德Lyapunov 指数，因此具有更复杂的相空间[7]。利用超混沌系统进行加密，可以具有更大的密钥空间和较强的不可预测性，能够生成更高性能的伪随机密钥流序列[8]。利用四阶龙格-库塔公式对Chen 超混沌系统进行离散化处理，迭代步长为0.0001，根据设置好的系统初值经过N 次迭代后得到混沌序列。利用该混沌序列可以生成性能良好的伪随机序列。

2.2 伪随机序列生成

基于分数阶Chen 超混沌系统，采用位序列生成算法[9]构造伪随机数序列，生成过程如下：

（1）确定系统的控制参数和初始条件，并指定所需要的序列长度。

（2）迭代1000 次以消除暂态效应。继续迭代超混沌映射系统，得到四个小数Ax，Ay，Az，Aw。

（3）小数的部分位数作为新的小数：为了最大限度的利用混沌系统的复杂性，去掉小数的前3 位。得到Bxy，Bzw

xn+1=xn+1×1000-floor(xn+1×1000)

（4）将该小数转化为长度为32 位二进制序列得到二进制序列Bx, By, Bz, Bw。

（5）异或得到最终的32 位二进制序列。

（6）继续迭代超混沌映射系统，重复上述步骤直至获得所需长度的超混沌伪随机序列。

2.3 NISTSP 800-22测试

NISTSP 800-22 是美国NIST 发布的关于序列随机性测试工具[10]。其中列出了15种单独的随机性测试，测试结果均以P-value表示。显著性水平α 通常取值为0.01，若P-value ≥α,则测试通过，该序列被认为几乎是随机的，置信度为(1-α)×100%。使用上述方法，初值x0=0.3, y0=-0.6, z0=1.8, w0=1.2, r0=0.3，步长0.0001，经过10000次迭代消除暂态效应后，构成的伪随机数序列测试的结果如表2所示。

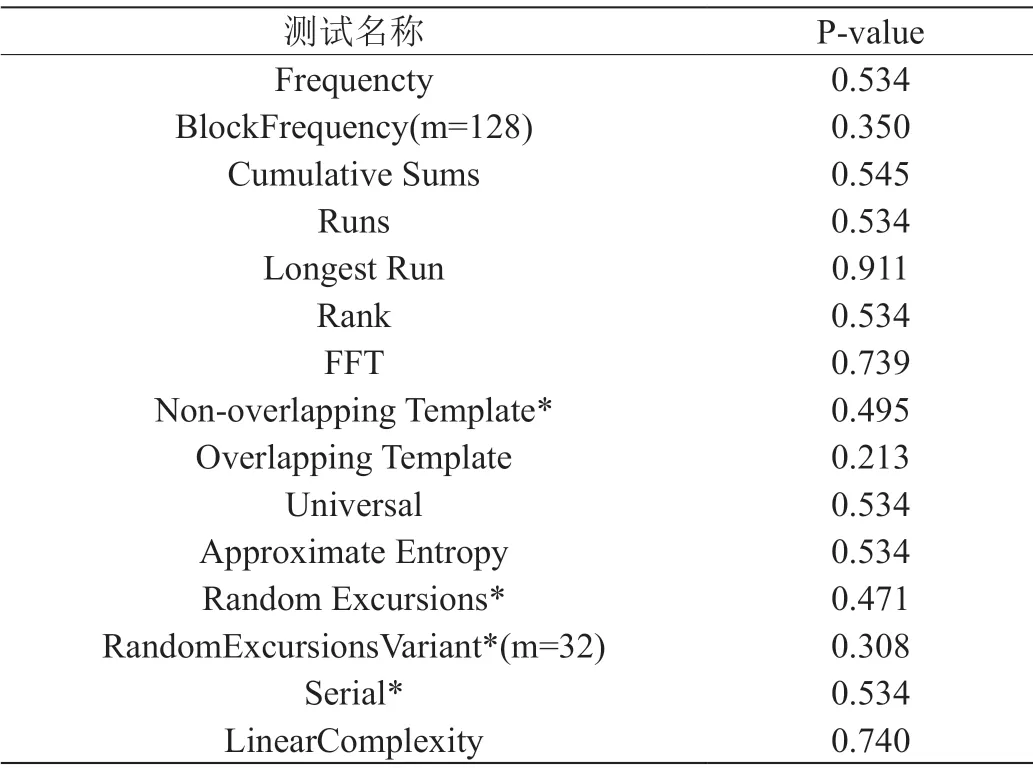
表2：NISTSP 800-22 测试结果

表2测试根据NISTSP 800-22 文档要求，使用推荐的块大小，序列长度进行测试，m 为块个数。其中，*表示列出的是多项测试的平均值。

如表2所示，基于Chen 超混沌系统产生的伪随机序列通过了NIST 测试，证实该序列能够满足随机序列相关特征，即生成的密钥流序列是几乎随机的。

3 基于Chen超混沌系统序列的AES加密算法

3.1 算法设计思想

AES 中轮密钥与种子密钥之间存在很强的关联关系，为了解决这一缺陷，采用序列密码思想，利用一个随机的不可预测序列作为加密的密钥流改进AES 的密钥扩展算法，使得AES 具有一次一密加密的效果，更难被密码分析[11]。增强算法加密的安全性。由于每组的加密密钥不具有相关性，因此无法根据截获的轮密钥推断出整个密钥序列，增强了AES 算法加密的安全性。

现将明文和密钥流分组按照一定长度进行分组加密，通过伪随机数生成算法产生一个随机密钥流序列，加密的轮密钥使用该密钥流序列，加密算法是改进S 盒后的AES 加密算法。

3.2 加解密算法

步骤1：首先选取五个初始值x0, y0, z0, w0, r0作为伪随机数生成算法的初值。

步骤2：使用四阶龙格-库塔公式对分数阶Chen 超混沌系统求解，

经过N 次迭代，得到4 个混沌序列X,Y,Z,W。

步骤3：调用改进S 盒之后的AES 算法对明文Mi进行加密，其中密钥Ki, i=0,1,2,…,t。为使用伪随机数生成算法得到加密的密钥流，t 为需要加密的明文分组个数。加密后得到密文序列Ci。

加密的伪代码如下：

#生成混沌序列

X,Y,Z,W=proChenChaosSequence(x0, y0, z0, w0, r0)

i=0

while i ＜ t:

#生成伪随机密钥流序列

K[i]= propKey(X,Y,Z,W)

AES(Encrypt,M[i],K[i])#加密

i++

改进后的算法解密过程与加密过程相似，只需要将AES(Encrypt,M[i],K[i])换为AES(Decrypt,M[i],K[i])。

4 实验结果及分析

4.1 实验结果

为了验证算法的有效性，在PC 平台下运用该算法进行加解密实验，开发工具为JetBrainsPyCharm。当选择加密种子密钥x0=0.3,y0=-0.6, z0=1.8, w0=1.2, r0=0.3，分组长度为128bit，每次生成的密钥流序列总共为128*(Nr+1)=1408bit。现对100KB 的文本进行加密，加密的结果如图1和图2所示。

图1：加密前的文本信息

图2：加密后的文本信息

4.2 安全性分析

4.2.1 密钥空间

传统的AES 算法的密钥空间为2128。本文提出的算法中，可以充当密钥的参数包括x0, y0, z0, w0, r0以及基本迭代次数N。在64 位处理器中浮点数精度为10-16，r0的取值空间为[0.085,0.789]，因此总的密钥空间为1016×5×(0.789-0.085)≈2265。由于基本迭代次数的总长度与明文长度相关，因此N 的取值不确定使得密钥空间的大小具有不确定性，提高了破译密码的难度。本算法的密钥空间远大于传统的AES 算法的密钥空间，能够有效的抵抗穷举攻击[12]。

4.1.2 密钥敏感性

在上述实验的基础之上，针对加密后的密文进行解密时，对种子密钥做出微小的改变。选择

在上述实验的结果之上，针对解密时种子密钥x0 做微小的改变，令 x0=0.3000000001,其余种子密钥保持不变，解密的结果如图3所示。

图3：改变密钥后解密后的文本信息

如图3可以看到解密失败的结果，即在种子密钥发生10-10级别的微小改变时，无法对密文成功解密，证明算法的密钥敏感程度非常高。

4.1.3 雪崩效应

针对128Bit 的明文文本每次只修改一位，分别经过改进后的算法和原始AES 算法进行加密，测试过程中加密密钥保持不变，记录密文的变化位数，得到的测试结果如图4所示。

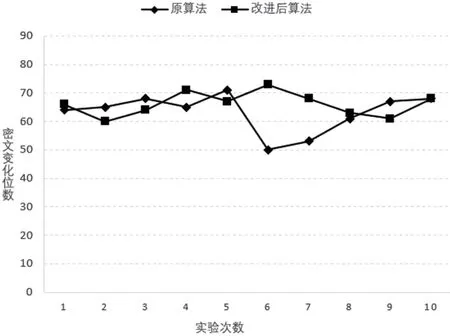
图4：雪崩效应测试结果

如图4所示，原始的AES 算法在改变一位原文后密文改变的位数波动范围为60±10，相较于原本的AES 算法，本文改进的算法在明文改变一位后密文改变为65±5 位，更加稳定，因此本文提出的改进算法符合雪崩效应的要求。

5 结论

本文改进了AES 算法的S 盒，显著增加了S 盒的迭代周期；利用Chen 超混沌系统生成伪随机密钥流，该随机序列通过了NIST测试，验证了其随机性，将序列密码的特点与传统AES 算法进行结合，实现了一种一次一密加密的效果。基于超混沌系统生成的密钥流具有庞大的密钥空间，同时综合了超混沌系统的初值敏感性和良好的随机性，使得改进后的密码体制具有更好的安全性能。每次加密过程中只需要生成一次混沌序列，因此对于算法的效率影响有限，该算法适用于对于安全性能要求较高的加密场景。