基于t-SNE降维的数据可视化分析研究

郭艳萍 高云 吕丙东

（山西大同大学计算机与网络工程学院 山西省大同市 037009）

1 引言

1.1 t-SNE背景

研究表明人类从外界获得的信息中80%以上都来自于视觉系统[2]。因为人类视觉只能接受3 维或3 维以下的信息， 超出3 维将无法直接观察[2]。然而，现实情况却是随意获取到的数据集，都可能会有成千上百个维度。如，经典的MNIST 维度是64，所以使用2 维的笛卡尔坐标系，注定无法绘制64 个维度。

如果想对高维数据集进行聚类，但又不清楚这个数据集有没有很好的聚类性时，可以通过降维算法将该数据集映射到2 维或3 维空间中。很久以前，就有研究者提出主成分分析（PCA）降维法，期间又有其他的降维算法陆续出现，比如多维缩放（MDS）、线性判别分析（LDA）和等度量映射（Isomap）等。

2008年，Laurens van der Maaten 和Geoffrey Hinton 一同提出了t-SNE 算法。他们将SNE 算法改进为t-SNE 算法，并使它在降维领域得到了更为广泛的应用[3][4]。

1.2 t-SNE概述

t-SNE 算法是一种降维技术，用于在2 维或3 维的低维空间中表示高维数据集，从而使其可视化。

t-分布全称为学生t-分布，是针对单个样本，而非总体样本的t 变换值的分布，是对u 变换变量值的标准正态分布的估计分布[5]。

t-SNE 的本质是一种嵌入模型，它在尽量保留样本集局部特性的基础上，将高维空间中的样本投影到低维空间中[5]。样本集经过t-SNE 变换后，如果在低维空间中仍具有可分性，则表明原始样本集是可分的；如果在低维空间呈现为不可分，则可能是由于样本集本身不具有可分性，或者样本集虽然具有可分性，但不适合投影到低维空间[3]。

2 t-SNE原理分析

t-SNE 将样本点之间的相似度转化为条件概率，高维空间中样本点的相似度由高斯联合分布表示，嵌入空间中样本点的相似度用t-分布表示[6]。即t-SNE 创建一个维度缩小的特征空间，相似的样本在该空间中使用其附近的点建模，相似度低的样本则由高概率的远点建模[5][7]。

t-SNE 为高维样本根据样本点之间的相似度构建一个概率分布，相似度高的样本被选中的概率就高，反之亦然。然后，t-SNE 在低维空间里根据概率分布构建这些点，使得这两个概率分布之间尽可能的相似[5]。最后，t-SNE 最小化了两个分布之间关于嵌入点位置的Kullback-Leibler（KL）散度。

通过原始空间和嵌入空间联合概率分布的KL 散度作为评估两个分布的相似度的指标，来评估嵌入效果。即将KL 散度函数作为损失函数[6]，通过梯度下降最小化所有样本点上的KLD 差异的总和[7]，最终获得收敛结果。

假设在一个2 维平面上有均匀分布的多个点，如果把这些点投影到一个1 维的线会导致很多点是重合的。所以，为了在1 维的线上尽可能表达出2 维平面中的点的信息，Hinton 采取的方法为，把由于投影所重合的点使用不同的微小距离来投影[3]。原来在那些距离上的点会再增加一个微小的距离，被赶到更远一点的距离。

t-分布是长尾的，意味着即使距离更远，那些点依然能给出和高斯分布下距离小的点相同的概率[7]。

假设如图1所示的是一个由3 个不同的类在2 维空间上组成的数据集群。

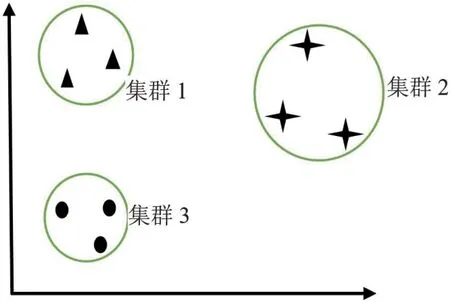
图1：3 个不同的类组成的数据集群

接下来希望将该数据集由2 维空间映射到1 维空间上，同时保持集群之间清晰的边界达到如图2所示的结果。

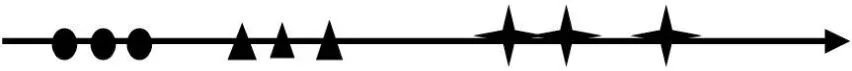
图2：二维投射到一维上

映射的方法有很多种，最简单的是如图3所示的将数据投射到一个轴（纵轴）上来降低维数。很显然，这是一种糟糕的方法，因为这样做会导致大量的信息丢失，并且可能导致数据集进行错误的划分[7]。

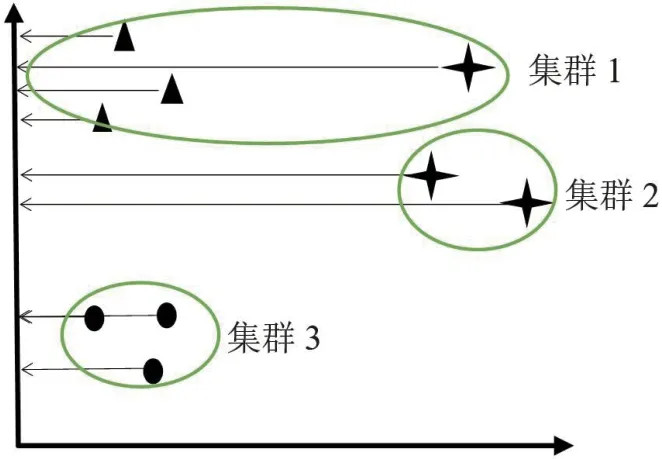
图3：对象到纵轴的映射

而使用t-SNE 算法可以实现如图2所示的要求。t-SNE 算法的第一步是计算一个点相对于其他点的欧几里得距离。计算后不是直接处理这些距离，而是将它们转换为条件概率来表达点与点之间的相似度，即映射到一个概率分布。在分布中，相对于当前点距离最小的点有很高的可能性，而远离当前点的点有很低的可能性。在图3所示的2 维图中，星型的点团比三角形的点团更加分散。如果不解决比例上的差异，三角形点的可能性将大于星型点的可能性。为了解释这一事实，将图4和图5所示点的概率分布除以概率的总和，计算公式及结果分别如公式（1）和公式（2）所示[7]。

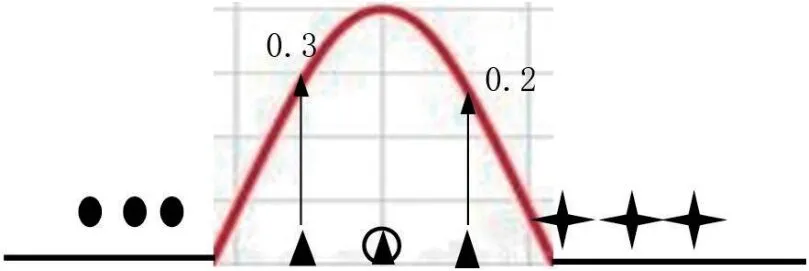
图4：三角形点概率分布图

图5：星型点概率分布图

可以看出，尽管图4和图5中两点之间的绝对距离不同，但其概率分布除以概率总和的值是相同的，因此它们被认为是相似的[7]。

接下来，使用缩小的特征空间。

图6：9×1 的矩阵

采用如上所述的方法，即测量点之间的绝对距离并将它们映射到一个概率分布中，需要注意的是，这样做并不是意味着，要将数据集中所有点的可能性的总和除以所有其他点的可能性。接下来考虑的是如何简化特征空间中的点的概率分布使其近似于原始特征空间中的点，就可以得到定义良好的聚类了[8]。

为了做到这一点，使用了KL 散度值。KLD 值是用来衡量一个概率分布与另一个概率分布之间的差异，即比较两个概率分布的接近程度。

在统计应用中，经常需要用一个简单的、近似的概率分布f*来描述观察数据D 或者另一个复杂的概率分布f。此时，需要使用一个量来衡量所选择的近似分布f*和原分布相比究竟损失了多少信息量，这就是KL 散度的作用。

KL 散度不具有交换性，不能将其理解为“距离”的概念，它衡量的并不是两个分布在空间中的远近，更准确的理解还是衡量一个分布相比另一个分布的信息损失（infomation lost）。

从图7和图8所示的两个KLD 中可得，KLD 值越小，两个概率分布的差异越小，越接近。当KLD 值为0 时，意味着这两个概率分布是完全相同的。

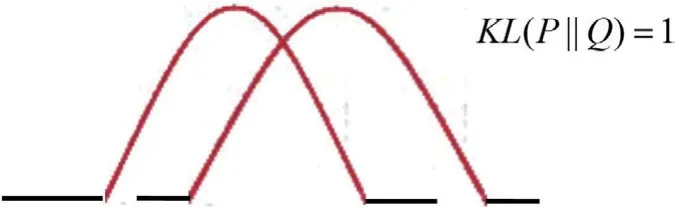
图7：

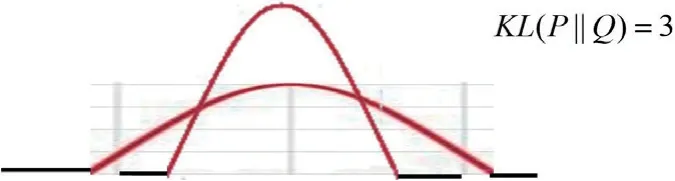
图8：

通常情况下 t-SNE 算法往往需要多次迭代并重复计算, 通过梯度下降达到最小化KL 散度的目的，取效果最好的一次结果。一旦该过程完成，将其映射回一个2 维或3 维空间。

3 t-SNE算法推导

t-SNE 是在SNE(Stochastic Neighbor Embedding, SNE; Hinton and Roweis)算法的基础上发展而来的。

数学上，正态分布的方程式如公式（3）所示。

基于该假设，近邻点之间会有较高的pj|i，而相互远离的点的pj|i随着距离的增加逐渐减小。在低维空间根据样本点在高维空间中的条件概率重置其位置，即t-SNE 降维的主要思路是测量点之间的距离并将它们映射到一个概率分布，实现高维空间到低维空间的特征映射。条件概率pj|i计算如公式（4）[4]所示。

其中，σi是以xi为中心的高斯函数的方差。

t-SNE 算法采用对称的SNE 计算，同时，在高维空间采用高斯概率分布, 低维空间下采用更重长尾分布, 即自由度为1 的t-分布，来解决SNE 的“crowding problem”问题。这种处理减弱了模拟的低维空间中映射点之间的吸引力[4]。低维特征空间映射点之间的概率qij对高维空间数据点之间的概率pij，如公式（5）[4]和公式（6）[4]所示。

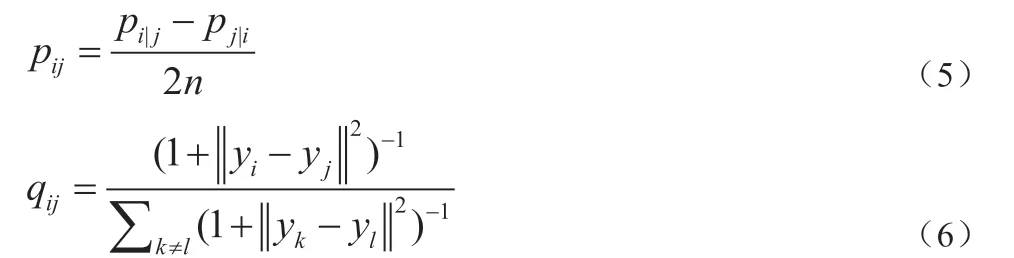
t-SNE 降维算法采用KLD 值测量并量化联合概率qij对pij映射的正确性[4]。

描述该正确性的量纲使用一个概率分布所对应的熵H，其表达如公式7 所示[13]。

当使用2 作为对数的底时（log2），熵可以被理解为编码所有信息所需要的最小位数（minimum numbers of bits）。KL 散度计算公式就是熵计算公式7 的简单变形，在原有概率分布P 上，加入近似概率分布Q，计算其每个取值对应对数的差：

换句话说，KL 散度计算的就是数据的原分布与近似分布的概率的对数差的期望值。当对数log 以2 为底时（log2），可以理解为“损失了多少位的信息”，将其写成期望形式为：

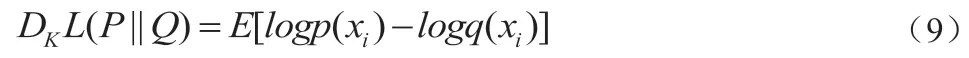
公式（9）更常见的形式为：

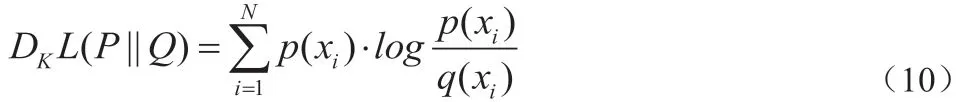
KLD 计算如公式（11）[10]所示。

在t-SNE 中，使用KL 散度的函数作为loss 函数，降维效果评判中，KLD 越小，两个分布越接近，即模拟正确性越高。KLD 为0 意味着这两个分布是相同的。利用梯度下降方法进行多次迭代，最小化所有数据点的KLD[4]，再计算梯度下降最小化所有样本点上的KLD 差异的总和，得到最佳低维空间映射。

对loss 函数的每一点求偏导，得到每次更新的方向，梯度下降方法如公式（12）[4]所示，yi为低维空间中的映射数据，随着KLD下降迭代不断优化。

t-SNE 算法通常需要多次迭代获得最好的收敛效果[4]。值得注意的时，该loss 函数不是凸函数，即具有不同初始值的多次运行将收敛于KL 散度函数的局部最小值中，可能导致获得不同的结果。因此，尝试不同的随机数种子有时候是有用的，并选择具有最低KLD 值的结果。

4 使用t-SNE实现手绘数字降维可视化

t-SNE 模型是非监督的降维，不需要预先指定分类标签信息[10]。与K-Means 等算法不同的是，它不能通过训练得到模型之后再将该模型用于其它数据， t-SNE 只能单独的对某个数据集进行操作，即它只能进行fit_transform 操作，而没有fit 操作。

4.1 实验环境

Intel(R)Core(TM)i7-8550U CPU@1.80GHz 2.00GHz 处理器，16.0GB 内存，Windows 10 Professional 操作系统，基于x64 的处理器， Anaconda3-5.2.0 环境进行算法编写运行。实验使用Python 中numpy 库、scikiti-learn 库、scripy 库、matplotlib 库 以 及seaborn 库实现。

4.2 实验数据

使用Python 的load_digits 数据集，该数据集是sklearn.datasets中内置的手写数字图片数据集，这是一个研究图像分类算法的优质数据集。

该数据集包含了1797 个样本，样本为ndarray 类型，保存8*8的图像，其元素是float64 类型，共有1797 张图片。

4.3 实验过程

4.3.1 使用scikiti-learn 库将手绘数字导入程序

该数据集的属性为 ['data', 'target', 'target_names', 'images', 'DESCR']；

样本数量=1797 ；

查看第一个样本数据，样本大小为8×8，即64：

[ 0.0.5.13.9.1.0.0.0.0.13.15.10.15.5.0.0.3.15.2.0.11.8.0.0.4.12.0.0.8.8.0.0.5.8.0.0.9.8.0.0.4.11.0.1.12.7.0.0.2.14.5.10.12.0.0.0.0.6.13.10.0.0.0.]。

t-SNE 严格用于可视化时，只能在至多3 维空间内进行显示，所以可视化维度只能降维2 或者 3，本文给定目标维度=2。算法的复杂度与算法中使用的最近邻的数量有关，不同的复杂度可能导致最终结果的剧烈变化，本文中将复杂度设为30。

4.3.2 调用拟合函数

表1：样本点之间欧氏距离表

根据表1所得的欧氏距离，使用复杂度为30 的参数值，进一步计算得到其联合概率pj|i值，结果如表2所示。

表2：联合概率pj|i

使用从标准偏差为10-4的高斯分布中随机选取值来创建缩小的特征空间本文创建的特征空间大小为1979×2，空间样本如表3所示。

表3：缩小的特征空间

定义自由度=1，经验表明，当自由度=空间维度-1 时，会得到更好的结果，本文的空间维度为2，因此计算得自由度为1。这里需要注意的是，如果空间维度为1 时，自由度也是1，而不能为0。

4.3.3 调用tsne 函数

将表3所示特征空间的样本向量拉平至一维，结果如表4所示。

表4：拉平至一维的特征空间

4.3.4 计算KL 散度和梯度的误差

梯度下降函数通过最小化KLD 值更新其中嵌入的值，当梯度范数低于阈值，或者达到可容忍迭代次数而没有取得任何进展时，将提前停止迭代。本文中设置最大迭代次数为1000，最小梯度范数阈值为10-7，最大无进展迭代次数为300。

每次迭代都会计算KLD 值和梯度形式的误差，本文实验次数达到最大迭代次数1000，迭代的部分结果如下：

首先计算高维空间中的样本在低维图中映射样本的概率分布，理论上算法可以处理任意小的正数，但是在实际处理过程中，Python 中计算机可表示的最小的正数为epsilon，小于该值的数字因为缺少必要的比特而不能被计算机操作。所以算法中检查了概率矩阵中的值是否小于epsilon，并在它们小于时替换它们，得到的结果如表5所示。

表5：低维图中映射样本的概率分布

将表5中的结果作为参数计算KL 散度，结果如表6所示。

表6：KLD 值

将表5中的结果作为参数计算梯度（偏导），结果如表7所示。

表7：梯度值

计算表7所示梯度的2 范数，得到结果如表8所示。

表8：梯度2 范数

利用梯度下降最小化KLD 值，从表6可以看出，随着迭代次数的增加，KLD 值逐渐减小，即低维空间映射样本的概率分布与高维空间原始样本的概率分布越来越接近。

最后，将降维后的手绘数字可视化展示出来，结果如图9所示。

图9：t-SNE 可视化手绘数字

5 t-SNE与PCA的比较

t-SNE 是目前效果最好的数据降维与可视化方法，本实验数据使用t-SNE 与PCA 的可视化结果如图10 所示。

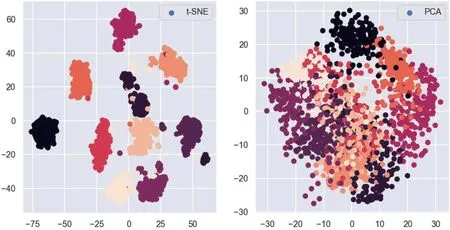
图10：t-SNE 与PCA 的可视化结果对比

从图10 可以看出，t-SNE 尽量保留了样本的分类特征。但是它的缺点也很明显，比如：

（1）t-SNE 的计算复杂度高，资源占用大，运行时间长，处理包含数百万个样本的数据集可能需要几个小时，而PCA 可以在几秒钟或几分钟内完成。

（2）t-SNE 通常只用于可视化应用，即映射空间只限于2 维或3 维。

（3）t-SNE 算法具有随机性，即不同种子的多次实验可能产生不同的结果。虽然最终选择损失最小的结果，但可能需要尝试不同的初始化点，进行多次实验以防止局部次优解带来的影响。

（4）全局结构未能明确保留，虽然这个问题可以通过PCA 初始化点来缓解，但不能根本解决。