集装箱船甲板长直通道无线覆盖仿真
朱 宇, 杨柳涛
(上海船舶运输科学研究所 航运技术与安全国家重点实验室, 上海 200135)
随着无线网络、物联网(The Internet of Things,IOT)、人工智能等信息与通信技术(Information and Communications Technology,ICT)在各行各业应用的不断深入,相关技术日益成熟,船舶行业和航运业正朝着信息化和智能化的方向发展,越来越多的信息化、智能化设备应用在船舶上。由于船舶的有线部署依赖于造船时预留的线缆孔,智能化和信息化设备的船上安装布设会受到影响。因此,全船无线覆盖是一种现实的需求。同样,由于线缆孔的限制,无线基站的铺设施工难度较大,既无法在实地直接进行,又无法在发现覆盖缺漏时补设。因此,有必要进行无线覆盖仿真,以提高船舶无线覆盖规划设计的准确性和有效性。
无线覆盖仿真的精确度与应用场景建模和传播模型等因素相关。传播模型是整个无线覆盖仿真的核心,采用合适的传播模型对于保证无线覆盖仿真的有效性而言尤为重要。由于船体为钢结构,对无线信号的传输有很大影响。现有的传统无线信号传播模型和距离损耗公式难以直接应用在船舶平台上。[1-2]
集装箱船甲板长直通道作为船舶无线覆盖的典型场景,具有钢制环境和隧道特性。在钢制类隧道环境中,电磁波的传播除了直射以外,还会经周围舱壁进行多次反射。因此,接收机接收到的电磁信号是经过多条路径、从多个方向传播过来的合成波,会有明显的多径效应。[3]基于国际电信联盟(International Teleconmunication Union,ITU)的ITU-R P.1238建议书,此类长直通道场景会产生菲涅尔损耗,对电磁波传播产生较大的影响。
目前,国内外对船舶长直通道信道的研究较少,但对隧道和矿井等类似场景有很多研究。文献[4]和文献[5]验证了采用射线跟踪法对隧道、走廊这类应用场景进行仿真的可行性。文献[6]和文献[7]对地铁隧道环境的信道进行建模仿真。文献[8]和文献[9]对密闭环境的可视信道进行建模仿真。文献[10]提出多模传输方式,以矩形波导实现对信号衰减的仿真,可对远场区进行较为精确的预测,但对近场区预测的误差较大。文献[11]以基于窄带信道的射线跟踪为基础,对超宽带矿井信道进行频率的模型修正。
隧道和矿井的反射壁以混凝土和矿物土层为主,反射能力较差,且反射壁的粗糙度较高,产生较大的漫散射影响。在相关传播模型仿真过程中,以直射路径分析和菲涅尔分析为主;船舶场景以钢制结构为主,反射壁的反射能力较强,且反射壁的粗糙度低,漫反射影响较小。集装箱船长直通道场景与隧道和矿井场景虽然在几何形状上类似,但在构成有效信号传播路径上存在较大差异,需对其进行仿真研究。
本文针对集装箱船甲板长直通道,对长期演进(Long Term Evolution,LTE)信道的大尺度路径损耗模型进行仿真研究。先对窄带信道的反射模型进行仿真,再根据ITU-R系列建议书,结合隧道环境的特点对传播模型进行损耗修正,最后建立针对集装箱船甲板长直通道的无线网络路径损耗预测仿真模型。
1 射线反射模型
目前,射线跟踪法是一种能有效进行无线覆盖仿真的方法[12-13],用于近似计算高频电磁场的传播。射线跟踪法根据几何光学(Geometrical Optics,GO)原理,认为电磁波的能量能以射线的形式向四周辐射,所有接收机与发射机之间的电磁波传播路径都可通过射线进行描述。在高频情况下,电磁波的传输特性和其他相关参量变化缓慢,其传播可通过射线模拟。先通过射线跟踪确定能到达接收机的有效传播路径,再对传播路径的传播衰减[14]进行计算,然后根据叠加原理完成对接收机所有路径信号能量的计算。
射线跟踪法主要分为正向传播和反向传播2种类型。
1)正向传播算法追踪发射机发射的每条射线,按照反射定律和几何绕射理论对遇到障碍物的射线进行处理,得出新的反射射线和绕射射线,并继续跟踪,直到该射线到达接收机的接收范围或该射线能量衰减至阈值以下。正向传播算法完成1次计算直接可得到全区域的无线覆盖情况,但精度受限且跟踪的射线量较多,整体计算的复杂度较大。
2)反向传播算法从接收点出发,反向跟踪所有发射机与接收机之间的传播路径,计算难度比正向算法更大,但能较为精准地得到点对点的传播路径和相应的相位、延迟等传播信息。[15]
本文选择反向传播算法作为仿真核心算法,采用镜像法完成对传播路径的计算。镜像法原理见图1。由图1可知:发射机的镜像位置与发射机的实体位置相对于反射面对称。发射机发射射线至反射面,再反射到接收机的传播路径,可直接等效为从发射机的镜像位置直接辐射到接收机。由发射机的辐射特性和反射面的电磁特性可得整体的1阶镜像辐射场。在实际传播中,射线会经过多次反射,因此,为模拟电磁波的实际传播过程,需对高阶反射进行计算。与1阶反射相似,先将发射机的镜像点作为虚拟发射机,计算该虚拟发射机相对于其他反射面的镜像点,再计算第2次反射的反射点,得到2次反射的传播路径。以此类推,完成对高阶反射的计算。

图1 镜像法原理
采用镜像法计算出发射机与接收机之间的有效传播路径之后,计算接收功率,有
(1)
式(1)中:Pr为接收机的接收功率;Pt为发射机的发射功率;λ为电磁波的波长;N为到达接收机的总传播路径数;Ri为通过反射面到达接收机的第i条射线的反射系数;ri为第i条射线的路径长;r为直射射线的路径长;ρs为粗糙反射面的散射损耗因数;φi为第i条射线路径与直射路径所传播信号在接收机处的相位差。
(2)
(3)
式(2)和式(3)中:σh为反射面粗糙度的方差;θi为第i条射线的入射角;Δli为第i条射线路径长度与视距路径长度的差值。
由于在实际传播中不存在理想导体,因此电磁波在反射过程中会产生损耗。通常情况下,反射损耗R用菲涅尔反射系数表示为
(4)
式(4)中:Er为反射电场强度;Ei为入射电场强度。
对于电磁波的入射波,采用平行和垂直2种极化方式,计算式为
Eh=Ehmcos(ωt-φh)
(5)
Ev=Evmcos(ωt-φv)
(6)
式(5)和式(6)中:Eh为平行极化波能量;Ev为垂直极化波能量;w为角频率;φ为初始相位。在线极化中,初始相位φh和φv均为0 ,即
(7)
在反射面上,根据传播路径的不同,电磁波会以不同的角度进行反射和入射。针对平行极化波和垂直极化波,其反射系数Rh和Rv分别为
(8)
(9)
式(8)和式(9)中:θ为电磁波的入射角;ε为反射面的相对介电常数。
将式(8)和式(9)分别代入式(7)和式(4)中,得到第i条电磁波整体在该入射角下对于反射面的等效反射系数,即
(10)
2 模型修正
根据ITU给出的ITU-R P.1238建议书,对于长的、具有走廊路径特征的无阻挡路径,可能会在距离发射机的某点开始产生菲涅尔损耗,即可能出现第1菲涅尔区的转折点。
菲涅尔区是在发射机与接收机之间,由电磁波的直射路径与折射路径的路径差为(nλ)/2的有效反射点形成的,其几何构成是以发射机和接收机的位置为焦点,以直射路径为轴的椭圆面。对信号传播影响最大的是第1菲涅尔区,即n=1的菲涅尔区。菲涅尔区同心的半径为
(11)
式(11)中:n为椭圆数目;d1为该菲涅尔区距离发射机的距离;d2为该菲涅尔区距离接收机的距离;λ为电磁波的波长。当电磁波波长确定时,位于发射机与接收机中间的第1菲涅区拥有最大的半径;当接收发机位置确定时,若电磁波波长变小,即电磁波频率提升时,则菲涅尔半径整体下降。
在电磁波的传播过程中,障碍物会对一些菲涅尔区发出的次级波产生阻挡,由此产生绕射损耗。由于第1菲涅区集中了在直射情况下的绝大多数能量,通常只要障碍物没有对第1菲涅尔区产生有效阻挡,绕射损耗就可忽略不计。当第1菲涅尔区被阻挡面积小于45%时,可认为电磁波传播无绕射损耗。
根据ITU-R P.526建议书,对于长直通道的菲涅尔损耗,可通过复合矩形孔径绕射模型进行近似拟合(见图2)。第1菲涅尔区的Fresnel-Kirchhoff绕射参数为
(12)
式(12)中:d1为该菲涅尔区与发射机之间的距离;d2为该菲涅尔区与接收机之间的距离;λ为电磁波的波长;H为障碍物顶部与发射机和接收机的连线的距离。

图2 矩形孔径绕射模型
孔径的刀刃位置如图2所示。原点为发射机与接收机的连线与屏蔽面的交点;电磁波的传播与z轴平行;发射机和接收机与屏蔽面之间的距离分别为d1和d2。接收机处的场强为
ea(x1,x2,y1,y2)=
0.5(CxCy-SxSy)+j0.5(CxSy+SxCy)
(13)
Cx=C(vx2)-C(vx1)
(14)
Cy=C(vy2)-C(vy1)
(15)
Sx=S(vx2)-S(vx1)
(16)
Sy=S(vy2)-S(vy1)
(17)
C(v)和S(v)由复数菲涅尔积分Fc(v)得出,有
(18)
x1、x2、y1和y2分别代替式(12)中的H,得出4个v值。单个矩形孔径的绕射损耗La为
La=-20lg(ea)
(19)
在整个复合矩形孔径传播模型的传播路径上,具有最大v值的单矩形孔径位置为主障碍物的位置,是整体绕射损耗的主要组成部分,记为a。
在近似处理复合模型损耗时,需计算2次单个矩形孔径处于最大v值时的绕射损耗。
1)从发射机到点a,得到vb和Lb。
2)从点a到接收机,得到vc和Lc。
复合矩形孔径模型的绕射损耗为
L=La+T[L(vb)+L(vc)+C]
(20)
C=10.0+0.04D
(21)
(22)
式(20)~式(22)中:C为经验较正量;D为总路径长度,km;T为2个副矩形孔径障碍物带来的损耗。
3 建模与仿真分析
3.1 集装箱船长直通道建模
根据21 000 TEU集装箱船的集装箱布置图纸,集装箱船长直通道主要有2种布置情况。
1)全封闭通道位于集装箱船内部下甲板处,整体体现为全封闭特征,舱壁为全金属材质。全封闭通道长约380.0 m;宽和高约为1个标准集装箱的宽和高,约为2.5 m。
2)半封闭通道位于集装箱船边缘,整体体现为半封闭特征(见图3)。顶部与集装箱关联的区域均为有效反射壁;侧部与集装箱关联区域均无有效反射壁;其余部位均为有效金属舱壁。半封闭通道长约380.0 m,宽和高与1个标准集装箱相同,约为 2.5 m。
根据集装箱船长直通道的特征,基于长直通道的几何结构,以有效反射壁为核心,通过3D建模软件分别对全封闭通道和半封闭通道进行建模图见图4。同时,为降低整体模型仿真的复杂度,减少计算,既不考虑长直通道中金属舱壁缝隙的不规律反射和散射特性,也不考虑长直通道内可能出现的各类小型杂物。

图3 集装箱船半封闭通道示意

图4 集装箱船半封闭通道3D建模图
3.2 仿真条件
电磁波在集装箱船长直通道的能量集中在通道的中心位置,因此在宽和高为2.50 m的通道中,节点均布置在通道中间高1.25 m处。发射机位置固定,接收节点在中线上,每隔1 m进行1次仿真。发射机和接收机均采用全向天线。由于受船载LTE专网频段的限制,此次仿真的电磁波频率取1.4 GHz。仿真参数见表1。
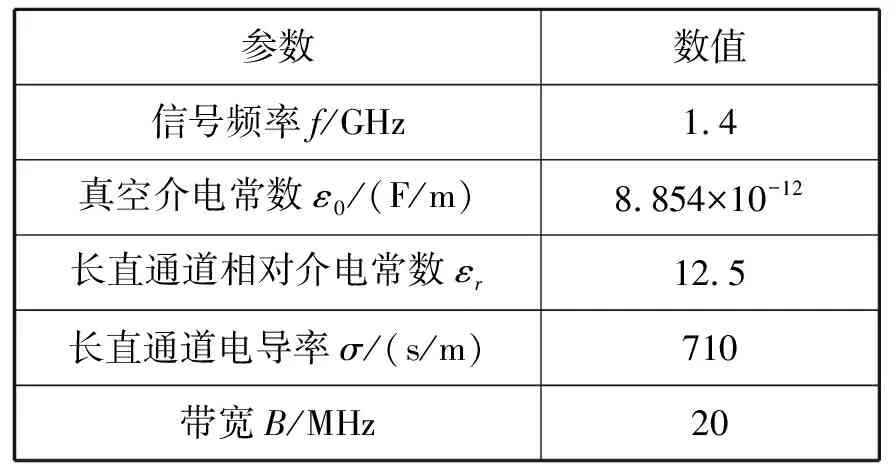
表1 仿真参数
考虑到舱壁对射线的反射损耗,反射次数超过3次以上的电磁波对接收机的影响较小[16],在仿真中取最大反射次数为3次。在传播过程中共有1条直达路径,4条1阶反射路径,8条2阶反射路径,12条3阶反射路径,共25条有效路径。长直通道射线跟踪法路径传播图见图5。
3.3 未修正的射线反射模型
采用射线跟踪法构建的射线反射模型分别应用在第3.1节构建的全封闭长直通道和半封闭长直通道中。由仿真结果可知:整体损耗明显呈现2种趋势:在80~100 m之前整体损耗呈现快衰落趋势,受多径干扰影响严重;在80~100 m之后整体损耗的浮动趋于稳定,损耗变化呈现满衰落趋势,损耗浮动情况与传播场景有相关性(见图6)。
3.4 模型的修正
在射线反射模型无线覆盖仿真中,并没有考虑第1菲涅尔区的阻挡情况。根据ITU-RP.526给出的建议:当第1菲涅尔区有效阻挡面积小于45%时,可认为电磁波传播无菲涅尔损耗;当第1菲涅尔区有效阻挡面积大于45%时,需对菲涅尔绕射损耗进行计算,并对射线反射模型进行修正。由式(11)可知:当电磁波波长确定时,发射机和接收机正中位置具有最大的第1菲涅尔区半径。以该半径为基准计算菲涅尔绕射损耗。

图5 射线跟踪法路径传播图

图6 未修正的射线反射模型
确定最大第1菲涅尔区半径与发射机和接收机的相对位置之后,在长直通道宽和高固定的条件下,可仿真得到不同频率下第1次产生有效菲涅尔绕射损耗的距离点,以及380 m长度下不同频率产生的菲涅尔绕射损耗。长直通道下频率与第1菲涅尔损耗点的关系见图7。由图7可知:当长直通道场景参数确定时,电磁波频率越高,第1菲涅尔损耗点距离发射机就越远,整体菲涅尔损耗越小。这是由于电磁波频率越高,其能量越集中,第1菲涅尔半径越小。在1.4 GHz频率下,第1菲涅尔损耗点在83 m处。
将射线反射模型与修正量结合,电磁波频率定为1.4 GHz,仿真得到距离变化与距离损耗的关系曲线见图8。由图8可知,修正模型的整体变化趋势与未修正模型相似:在第1菲涅尔损耗点之前,损耗曲线整体呈快衰落特征,受多径衰落的影响较大;在第1菲涅尔损耗点之后,损耗曲线特征与传播场景有关。在全封闭长直通道中,最大距离损耗为75.23 dB;在半封闭长直通道中,最大距离损耗为83.06 dB。与未修正模型相比,整体增加5~10 dB的菲涅尔损耗。

图7 长直通道下频率与第1菲涅尔损耗点的关系

图8 修正的射线反射模型
3.5 针对仿真结果的拟合与分析
路径损耗可通过对数距离模型进行拟合预测,表达式为
PL=PL0+10nlgd
(23)
式(23)中:PL0为参考距离的路径损耗,与电磁波频率和参考距离有关,参考距离一般取1 m;n为距离损耗因数;d为发射机与接收机之间的距离。
采用最小二乘法分别对全封闭通道和半封闭通道进行单斜率和双斜率对数拟合,并采用均方根误差(Root Mean Squared Error,RMSE)对拟合效果进行评价,表达式为
(24)
3.5.1全封闭通道拟合
通过单斜率拟合得到全封闭长直通道的路径损耗(见图9)和均方根误差,分别为
PLquan=23.70+18.43lgd
(25)
RMSEquan_dan=2.801 9
(26)
双斜率的模型以第1菲涅尔损耗点为转折点,拟合可得的全封闭长直通道的距离损耗(见图10)和均方根误差,分别为
(27)
RMSEquan_shuang=1.837 2
(28)
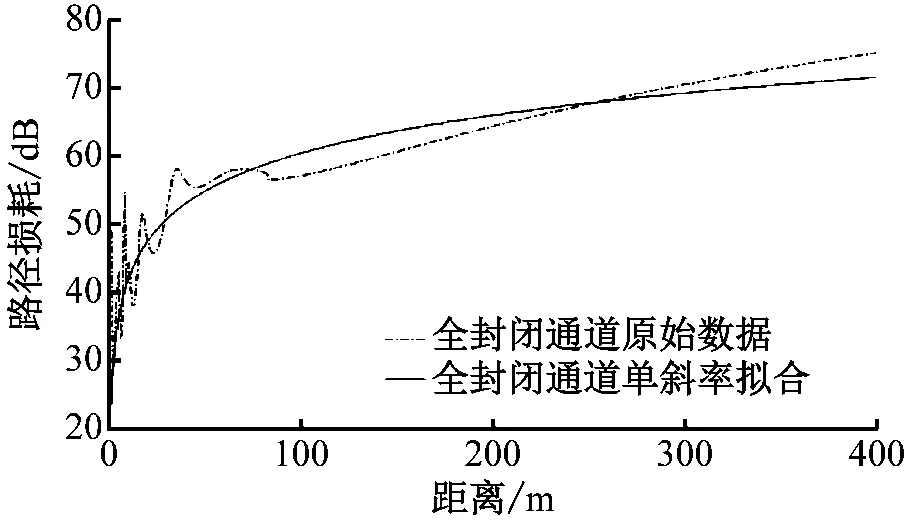
图9 全封闭通道的路径损耗
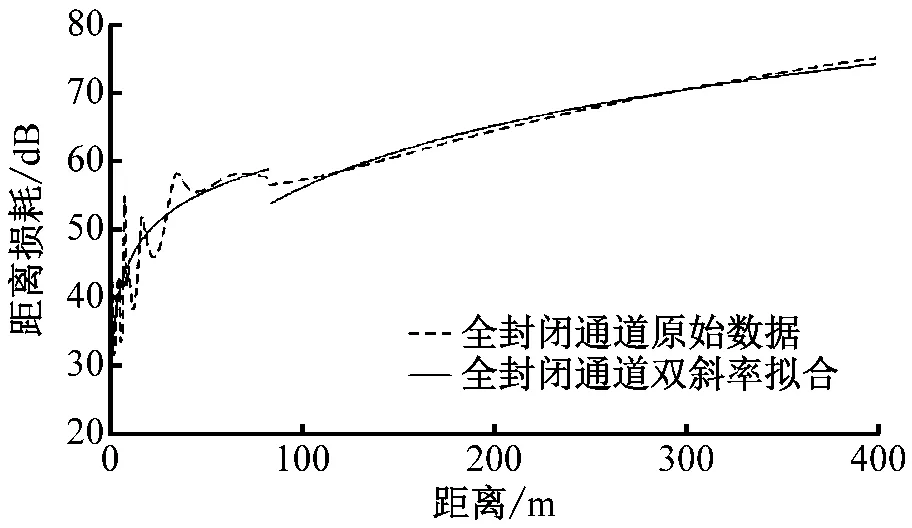
图10 全封闭通道的路径损耗
3.5.2半封闭通道拟合
通过单斜率拟合可得半封闭长直通道的路径损耗(见图11)和均方根误差,分别为
PLban=25.10+19.29lgd
(29)
RMSEban_dan=3.971 6
(30)
经过双斜率拟合得到半封闭长直通道的路径损耗(见图12)和均方根误差,分别为
(31)
RMSEban_shuang=3.069 9
(32)

图11 半封闭通道的路径损耗

图12 半封闭通道的路径损耗
3.5.3仿真拟合数据分析
在全封闭通道场景下,通过式(26)和式(28)可得单斜率和双斜率模型的RMSE分别为2.821 9和1.837 2;在半封闭通道场景下,通过式(30)和式(32)可得单斜率和双斜率模型的RMSE分别为3.971 6和3.069 9。对比2个场景和2种拟合模型的RMSE可知,采用双斜率对数距离损耗模型所得结果更接近仿真结果。
由式(27)可得全封闭双斜率模型的路径损耗因数分别为1.508和3.030;由式(31)可得半封闭双斜率模型的路径损耗因数分别为1.512和3.323。
在自由空间中,路径损耗因数n=2。由于本文所述场景为金属舱壁的集装箱船甲板长直通道,具有较多反射路径,可对直射路径进行补充,理论上在没有额外损耗的情况下n应小于2。由仿真结果可知:在第1菲涅尔损耗点之前,全封闭通道路径损耗因数为1.508,半封闭通道路径损耗因数为1.512,均小于2,符合ITU-R P.1238建议书给出的一般性结论,且全封闭通道的损耗因数仅比半封闭通道的小0.004,说明在第1菲涅尔损耗点之前反射分量充足时,传播场景的影响较小;第1菲涅尔损耗点之后,由于产生较大的菲涅尔损耗,全封闭通道的路径损耗因数为3.030,半封闭通道的路径损耗因数为3.323,均大于2,符合ITU-R P.1238建议书给出的一般性结论。全封闭通道相较于半封闭通道,路径损耗因数小0.293,体现出了传播场景的差异。
仿真研究结果表明:对于集装箱船甲板长直通道这一场景,采用修正的双斜率对数距离损耗模型可得到较为精确的预测结果。
4 结束语
本文基于射线跟踪法对集装箱甲板长直通道进行无线覆盖仿真。采用镜像法对电磁波传播路径进行计算,通过对直射传播和反射传播进行计算,得到该特定场景下点对点的距离损耗模型;计算该场景下的菲涅尔损耗,完成对射线反射模型的修正。在1.4 GHz电磁波频率下对全封闭通道和半封闭通道进行仿真分析,距离损耗因数均符合理论预期。基于仿真模型可确定:对于集装箱甲板长直通道,在380 m全封闭通道中最大距离损耗为75.23 dB,半封闭通道中最大距离损耗为83.06 dB。利用该模型可有效预测该场景下的信号覆盖情况,为不同尺度的集装箱船长直通道的无线基站布设和优化提供指导。

