大规模水下滑翔机集群区域覆盖探测路径规划

邹佳运, 曲泓玥, 陈志鹏

大规模水下滑翔机集群区域覆盖探测路径规划

邹佳运1,2, 曲泓玥2*, 陈志鹏3

(1. 中国人民解放军 海军潜艇学院, 山东 青岛, 266199; 2. 青岛海洋科学与技术试点国家实验室, 山东 青岛, 266237; 3. 海装沈阳局驻葫芦岛地区军事代表室, 辽宁 葫芦岛, 125003)

在水下滑翔机集群执行搜索任务时, 通过合理设定各平台的搜索路径, 能够有效提高集群的探测效能, 从而实现利用最少平台的最大化探测区域覆盖。为解决大规模集群任务规划中计算量巨大的问题, 文中在栅格法的基础上, 通过几何划定有效覆盖区域并反演栅格序数的方法, 构建了评价覆盖能力的高精度布尔模型, 并以此为支撑, 利用群智能方法实现了大规模集群对广域海区的快速路径规划。在此基础上, 利用序贯思想, 提出了以较小计算量解决集群平台数量最小化的方法。通过仿真试验验证了该方法的可行性。文中的方法可为大规模水下滑翔机集群的探测任务规划提供支持。

水下滑翔机集群; 探测; 任务规划; 区域覆盖

0 引言

水下无人平台能够在恶劣环境下完成长时间的警戒任务[1], 成本较低, 但随着水下探测任务的复杂化, 单一的水下无人平台已无法应对多样的任务需求[2]。水下无人集群技术以其高鲁棒性、高效率和低成本的特点[3], 越来越受到人们的重视, 并广泛应用于海洋观测、搜救、反潜及扫雷等领域[4]。

近年来, 以水下滑翔机为代表的低速、长航程无人水下航行器, 以其更长的工作时间和更广阔的搜索区域, 受到了越来越多的青睐。此类平台在使用时, 一般采用顺流布放的方式借助海流增加航程, 但对于集群探测问题, 受目标海区边界及各平台航路间的相互影响, 单纯地顺流布放可能导致大量的平台冲出目标海区和航路重叠问题, 从而降低集群搜索效能。在一定条件下, 一定角度的侧流航行虽然无法达到单平台的最大区域覆盖, 但若能够有效地填补平台间的空隙, 则能够使得集群整体的探测效能最大化。

为提高该类别无人集群对水下目标的探测效能, 需要对集群的搜索路径进行优化, 以期利用最少的平台数量实现区域覆盖最大化。目前, 对水下无人集群的区域覆盖能力研究集中于组网的静止节点部署[5-6], 路径规划则集中于解决避碰、避障问题[7-8], 而对移动平台的探测区域覆盖能力研究较少, 若能够根据海区条件及无人系统的性能参数对任务进行合理规划, 则能够有效降低任务成本, 提高任务效能。移动平台的最大化区域覆盖任务规划能力能够对低机动能力目标(如水雷、黑匣子等)的区域内搜索提供参考。

1 集群探测覆盖模型

目前一般利用栅格法对无人集群的探测效能进行评估。该方法将待评估海区栅格化, 令目标在全部栅格中遍历, 以探测系统对各栅格内目标的探测能力来评价其探测效能。单无人平台的探测半径一般为3~5 km, 为获得较为连续的有效探测区域边界, 栅格边长需要数百米, 但大规模集群的目标海区面积可能高达数万平方公里, 这就会导致栅格数目极多, 进而在进行栅格遍历时产生极大的运算量。

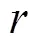
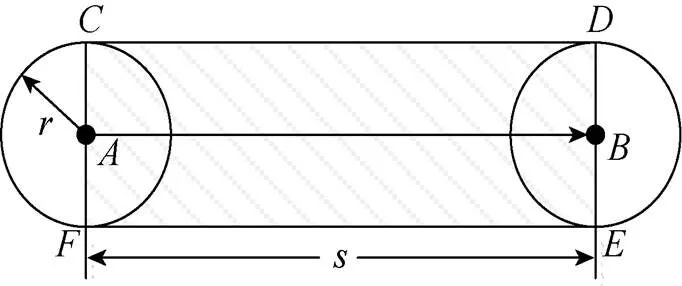
图1 有效探测区域示意图

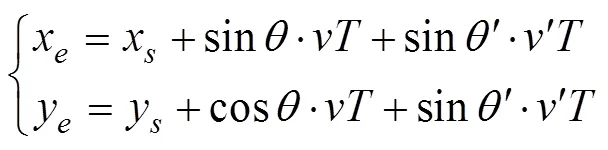
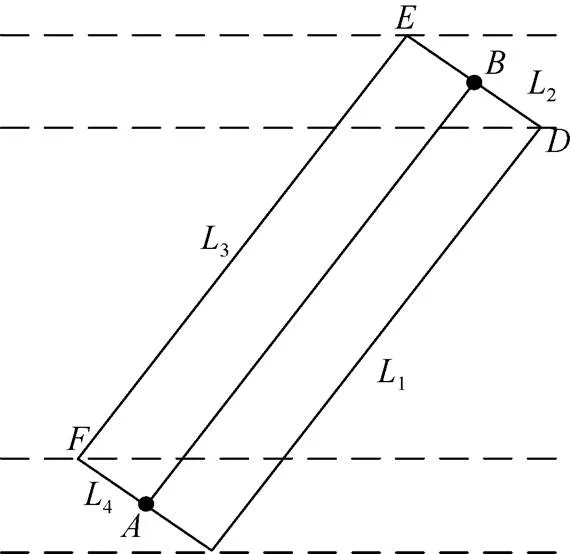
图2 有效探测区域评估示意图

可以求得各顶点的坐标分别为

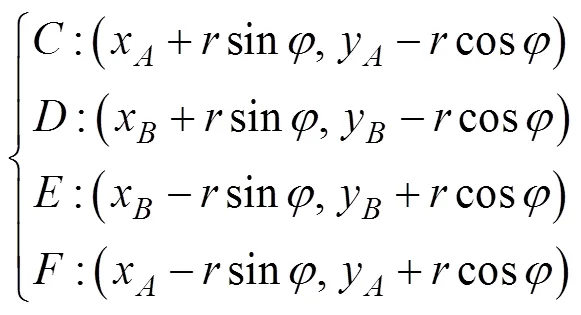
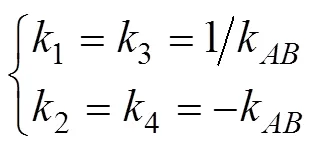
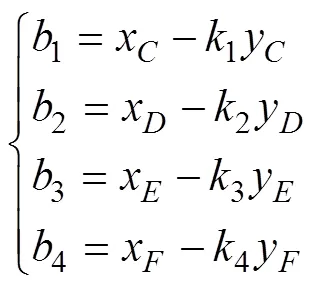
在确定各边解析式后, 即可计算有效评估区域内栅格的集合。

有效探测区域筛选方法如下:

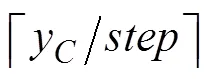
算法流程如图3所示。

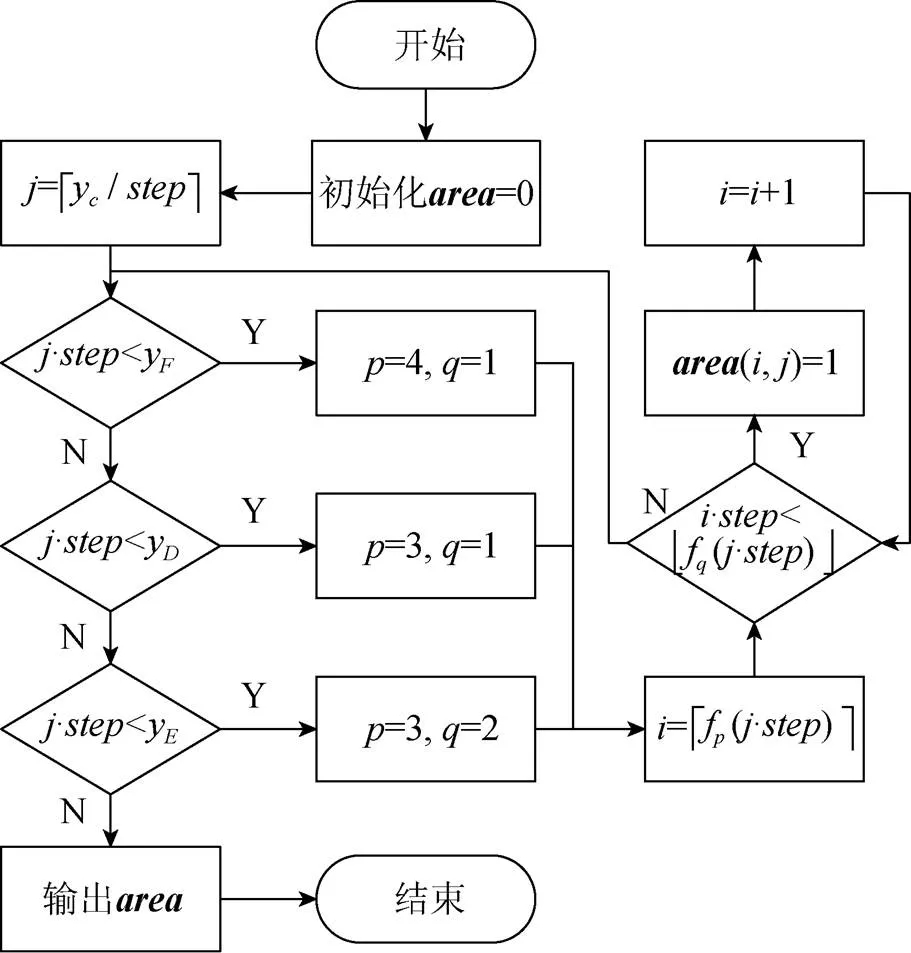
图3 评估算法流程图

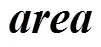
2 集群探测路径规划

对于集群探测系统, 各平台的起始位置及航向决定了该轮探测集群对目标海区的覆盖能力, 为提高效能, 需要求解使得总有效探测面积最大的一组起始位置和航向解。在该问题中, 每个平台有横坐标、纵坐标及航向3个变量, 若集群规模较大, 会使得传统的数学规划等方法难以实现寻优, 为解决该问题, 通常采用粒子群优化(par- ticle swarm optimization, PSO) 算法。

2.1 规划算法

PSO算法是由Kennedy等[9]提出的一种应用广泛的群智能优化算法, 该算法通过模拟鸟类觅食过程中各个体追随自身历史最优解及群体最优解的过程实现优化。

假设集群有个平台, 每个平台需要起始点横、纵坐标以及搜索航向才能确定搜索区域, 故第次迭代后, 第个粒子的位置矩阵

相应定义粒子的运动速度矩阵

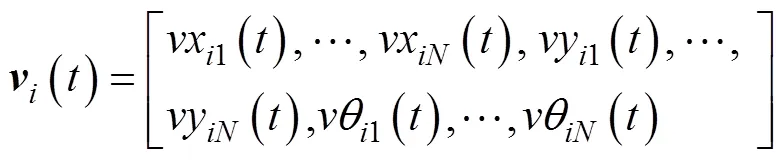
矩阵中的每个元素对应着位置矩阵中各元素的更新速度, 速度矩阵在迭代过程中依据式(7)和式(8)进行更新

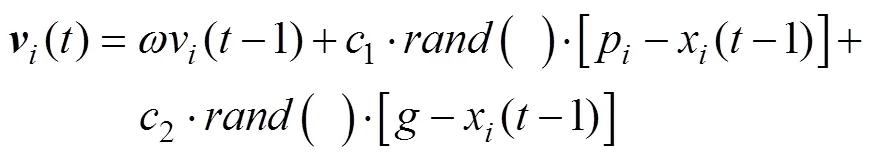
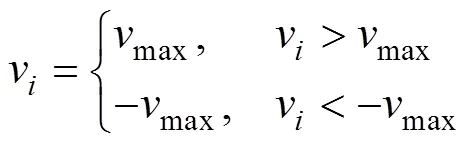
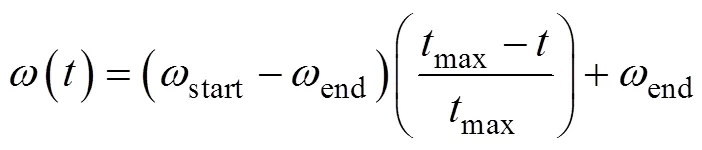
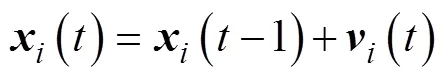
由此不断迭代, 位置矩阵中的解会不断向最优解搜索靠近, 经过足够次数的迭代, 即可得到足够接近最优解的近似最优解。

2.2 算例分析

图4展示了优化前后的集群区域覆盖效果, 红色线条为各平台航迹, 黄色区域为有效覆盖区域, 蓝色区域为未覆盖区域。图4(a)为粒子随机初始化时, 各粒子中的最优解, 此时的航迹分布较为分散, 有效覆盖率为40.24%; 图4(b)为经过500次迭代优化后获得的优化结果, 优化后, 航向大多趋向于顺流, 相互之间填补了空隙, 这有利于提高搜索路程, 航迹间的交叠与冲出目标海区的情况减少, 虽然不是所有平台的航向都严格地与流向相同, 但航迹的位置分布合理, 相互有效地填补了空隙, 有效覆盖率提高到62.28%, 达到了较好的总体效能。

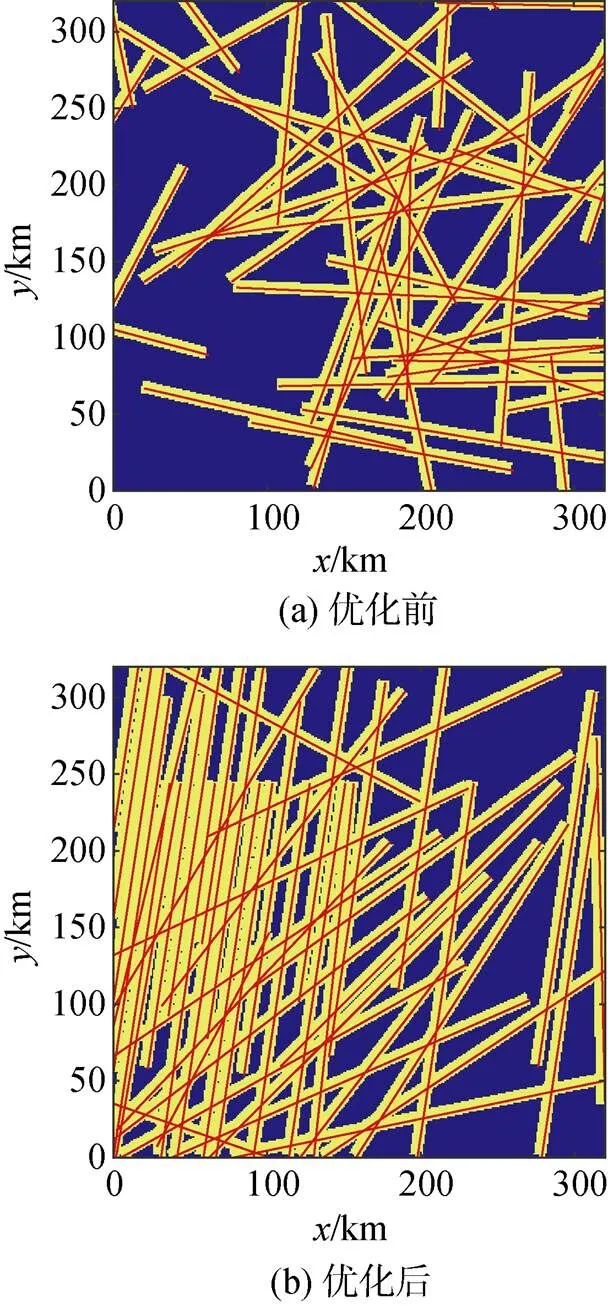
图4 优化前后覆盖效果图

图5为优化后的区域覆盖率随迭代次数的变化规律。随着迭代的进行, 各粒子不断向最优解靠近, 在一定次数的迭代后, 粒子已足够接近最优解, 故进化曲线趋于平缓, 通过多次测试, 进化曲线都会在500次迭代内收敛, 故对该问题推荐进行500次迭代优化。基于该快速评估模型的500次粒子群优化仅用时46.1758 s。

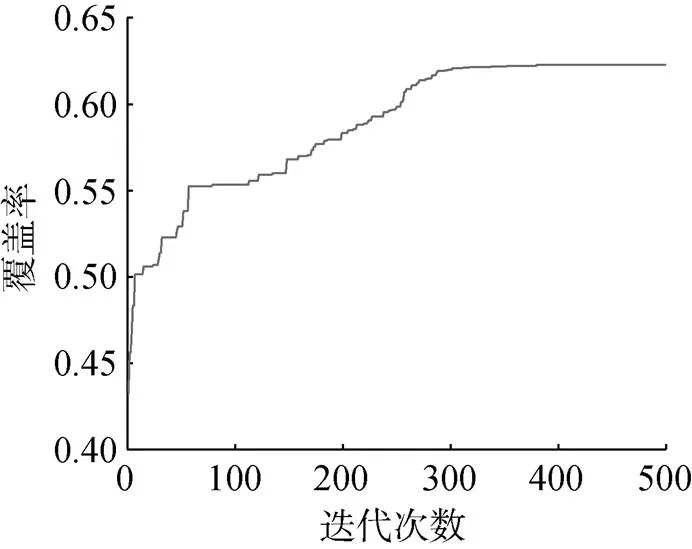
图5 优化后区域覆盖率随迭代次数的变化规律

3 集群平台数量优化

3.1 规划算法

为追求任务中的最小资源投入, 需要通过合理安排搜索任务使得所需的平台数量最少。上一节中的路径优化方法需要已知的平台数目, 而在该问题中, 平台数目及各平台的搜索策略均为待优化变量。

为解决最少平台数目未知的问题, 这里采用序贯的思想: 先以一定数目的平台进行路径规划, 在此基础上依次添加平台至最优位置, 直至达到覆盖要求。

平台数量优化的步骤如下(参见图6):

4) 在步骤3)的最优方案基础上, 新增一个平台,利用PSO算法进行单平台路径优化, 使得该新增平台能够最大化覆盖步骤3)方案中的探测盲区, 并记录新方案;

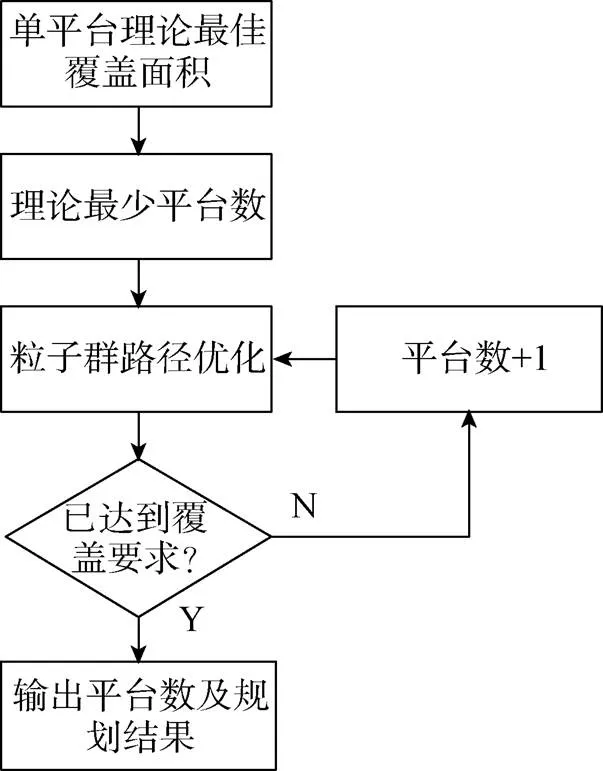
图6 平台数量优化流程

5) 判断新方案是否满足任务覆盖需求, 是则输出覆盖方案, 反之则回到步骤3)。

3.2 算例分析

海区条件、水下滑翔机平台参数同2.2节中算例, 现要求有效覆盖率达到85%, 对平台数量及平台搜索路径优化。

图7为对42个平台进行预优化的进化曲线, 经过500次迭代, 进化曲线已收敛, 且集群的覆盖能力达到59.57%, 为进一步求解覆盖率达到85%所需要的最少平台数目, 依次在之前已形成的搜索策略基础上添加1个平台, 并对新增平台的起始位置、航向进行优化。序贯过程中, 随平台数目递增, 区域覆盖率的变化规律如图8所示逐步提高, 当平台数增至67个时, 区域覆盖率首次超过85%达到85.30%。

由此得到结论: 最少利用65个平台可以达到预定区域覆盖需求, 最优覆盖方案如图9所示, 优化过程总用时53.22 s。

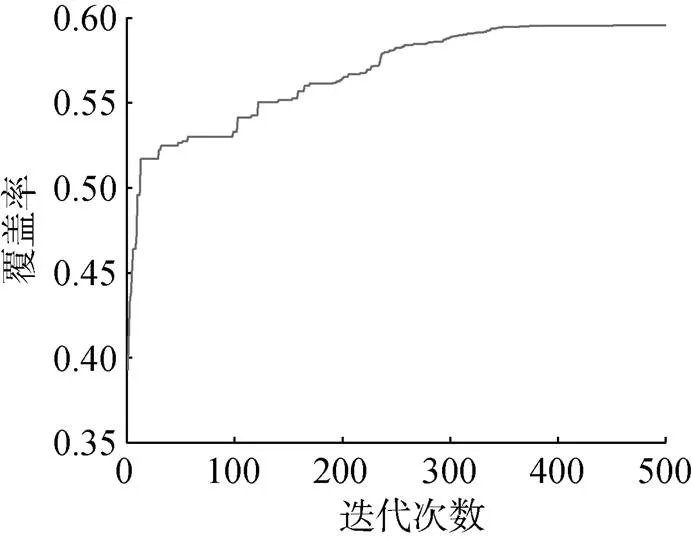
图7 未知平台数下预优化进化曲线

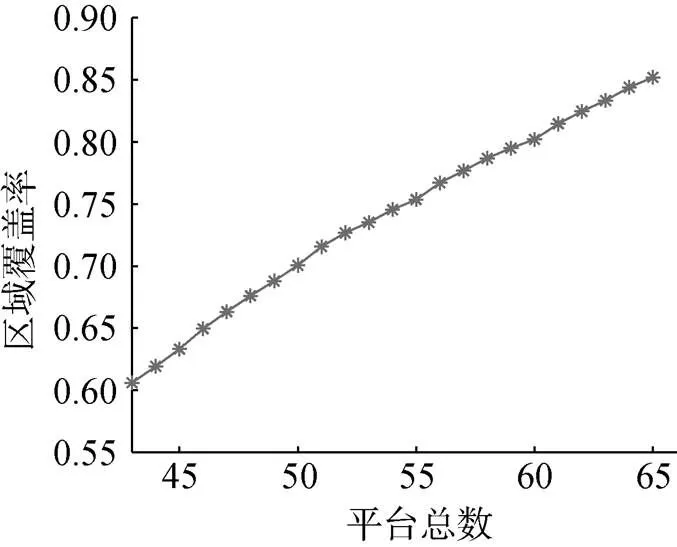
图8 未知平台数下覆盖率随平台数变化规律

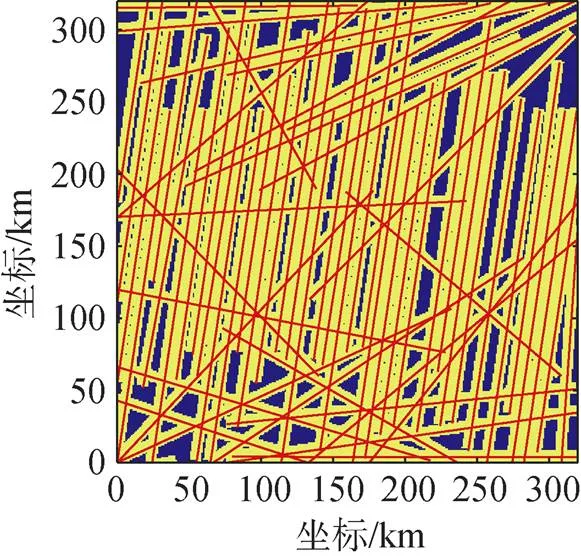
图9 未知平台数下满足覆盖需求的覆盖方案

在流速更高的环境下, 水下滑翔机能够获得更高的顺流航速, 单平台的效能更高, 故所需平台更少。图10可见, 经过500次迭代, 算法将初始35个平台的覆盖能力优化到了60.28%, 而后依次添加平台并利用PSO算法规划至最优航路。序贯过程中, 随平台数增多, 区域覆盖率的变化过程如图11所示, 当平台数目增至54个时, 区域覆盖率首次超过85%达到85.04%。

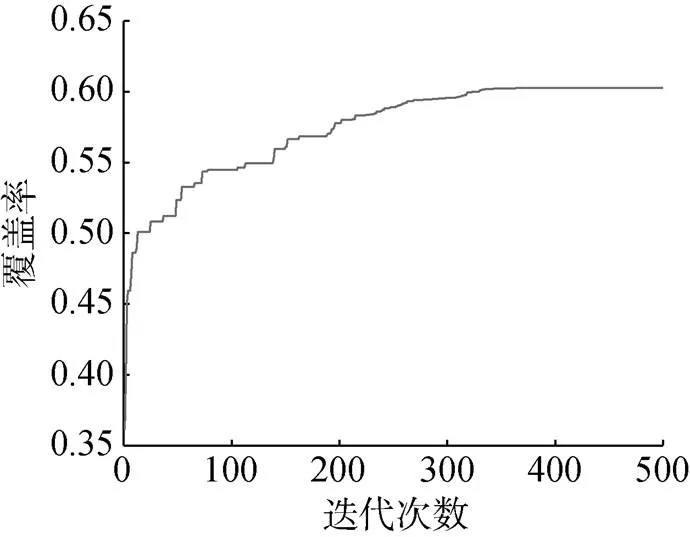
图10 更高海流流速下预优化进化曲线

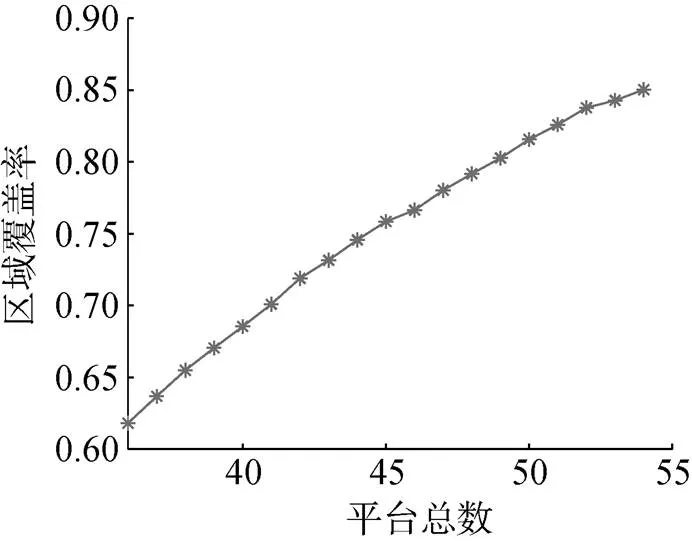
图11 更高海流流速下覆盖率随平台数变化规律

最优航路方案如图12所示, 相比于0.2 m/s的海流, 0.4 m/s的海流使得单平台拥有更大的覆盖区域, 多数平台趋向于海流方向有序排列, 部分平台则填补平台间空隙, 使得集群的总覆盖面积最优。

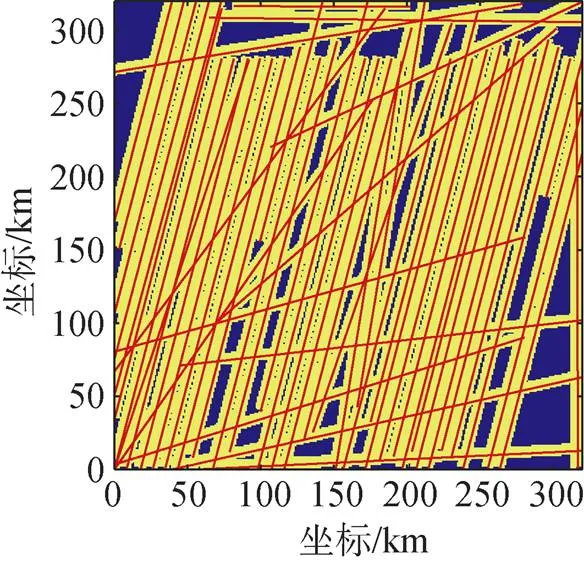
图12 更高海流流速下满足覆盖需求的覆盖方案

4 结束语

合理地安排水下滑翔机集群中各平台的搜索路径, 能够有效提高集群探测的搜索效能, 并可在满足任务需求的前提下降低平台需求量, 节约任务成本。文中通过划定有效探测区域, 反演有效探测区域内栅格序数的方法, 实现了对大区域、大集群探测覆盖问题的快速优化。在该优化模型的基础上, 利用序贯思想, 采用依次添加平台至最优位置的方法, 实现了最少平台数目的区域覆盖优化。通过算例分析, 优化算法能够有效地提高区域覆盖率, 且优化速度快, 对于约10×104km2的海区、45个平台的大规模系统, 能够在1 min内给出精度为500 m的优化方案; 在给出预期的区域覆盖率后, 最少平台数量优化算法成功地给出了低资源消耗的区域覆盖方案。

反演栅格序数的区域覆盖能力评估方法具有快速、高精度的特点, 但该方法为降低运算量, 简单地规定平台只能沿直线运动, 一定程度上限制了集群的灵活性, 使得该方法仅适用于对平台转向需求较弱的开阔海区。有效探测区域的矩形近似, 使得探测效果评估仅能使用布尔感知模型, 无法体现集群多源信息融合对目标探测的增益。

[1] Ridao P, Carreras M, Ribas D, et al. Intervention AUVs: The Next Challenge[J]. Annual Reviews in Control, 2015, 40: 227-241.

[2] 周菁, 慕德俊. 多机器人系统任务分配研究[J]. 西北大学学报(自然科学版), 2014, 44(3): 403-410.

Zhou Jing, Mu De-jun. Study of Multi-robot System on Task Allocation[J]. Journal of Northwest University(Na- tural Science Edition), 2014, 44(3): 403-410.

[3] Sotzing C C. The Design and Implementation of A Multi-Agent Architecture to Increase Coordination Efficiency in Multi-AUV Operations[D]. Edinburgh, Scotland: Her- iot-Watt University, 2009.

[4] 金建海, 陈伟华, 张波, 等. UUV集群技术概述[C]// 2018年水下无人系统技术高峰论坛论文集. 西安: 水下无人系统技术高峰论坛, 2018: 32-36.

[5] 生雪莉, 李鹏飞, 郭龙翔, 等. 基于单平台探测概率模型的水下无人集群部署规划算法[J]. 水下无人系统学报, 2019, 27(2): 194-199.

Sheng Xue-li, Li Peng-fei, Guo Long-xiang, et al. Deployment Planning Algorithm of Unmanned Underwater Swarm Based on Probability Model of Single-platform Detection[J]. Journal of Unmanned Undersea Systems, 2019, 27(2): 194-199.

[6] Dong W, Sheng X, Jiang X, et al. Energy Constrained Multi-Platform Network Underwater Detection Performance[C]//International Conference on Underwater Networkd & Systems. Rome, Italy: ACM, 2014: 43.

[7] 马焱, 肖玉杰, 陈轶, 等. 基于改进烟花-蚁群算法的海流环境下水下无人潜航器的避障路径规划[J]. 导航与控制, 2019, 18(1): 51-59.

Ma Yan, Xiao Yu-jie, Chen Yi, et al. Obstacle Avoidance Path Planning of Unmanned Underwater Vehicle in Ocean Current Environment Based on Improved Fireworks-ant Colony Algorithm[J]. Navigation and Control, 2019, 18(1): 51-59.

[8] 严浙平, 邓超, 迟冬南, 等. 双种群粒子群算法及其在UUV路径规划中的应用[J]. 计算机工程与应用, 2013, 49(15): 1-5.

Yan Zhe-ping, Deng Chao, Chi Dong-nan, et al. Two- Subpopulation Particle Swarm Optimization and its Application in UUV Path Planning[J]. Computer Engineering and Applications, 2013, 49(15): 1-5.

[9] Kennedy J, Eberhart R. Particle Swarm Optimization[C]// Proceedings of ICNN’95-International Conference on Neural Networks. Australia Council, Perth: IEEE, 1995.

[10] Shi Y, Eberhart R C. Empirical Study of Particle Swarm Optimization[C]//Evolutionary Computation, 1999. Proc- eedings of the 1999 Congress on Evolutionary Computation. Washington, DC, USA: IEEE, 1999.

Path Planning of a Large-scale Underwater Glider Swarm Area Coverage Detection

ZOU Jia-yun1,2, QU Hong-yue2*, CHEN Zhi-peng3

(1. Navy Submarine Academy, Qingdao 266199, China; 2. Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao 266237, China; 3. Military Representative Office of Shenyang Bureau in Huludao, Huludao 125003, China)

When search tasks in an underwater glider swarm are conducted, the detection efficiency of the swarm can be improved effectively by setting the search path of each platform reasonably, thereby maximizing the coverage of the detection area with the least platform.To solve the problem of large calculations in large-scale swarm mission planning, this study constructs a high-precision Boolean model based on the grid method to evaluate the coverage ability of an underwater glider swarm by delimiting the effective coverage area geometrically and inverting the grid number. With this as a support, a swarm intelligence algorithm can then be used to realize fast path planning of a large-scale swarm in a wide sea area. Accordingly, this research proposes a method for solving the minimum number of swarm platforms with only few calculations by using sequential thought. The feasibility of this method is verified through a simulation experiment. The proposed method can support mission planning for large-scale underwater glider swarms.

underwater glider swarm; detection; mission planning; area coverage

TJ630.33; TB566

A

2096-3920(2021)01-0023-07

10.11993/j.issn.2096-3920.2021.01.04

邹佳运, 曲泓玥, 陈志鹏. 大规模水下滑翔机集群区域覆盖探测路径规划[J]. 水下无人系统学报, 2021, 29(1): 23-29.

2020-04-16;

2020-06-02.

国家重点研发计划项目(2019YFC0311700); 青岛海洋科学与技术试点国家实验室“问海”计划项目(2017WHZZB0601).

曲泓玥(1995-), 女, 硕士, 主要研究方向为声呐系统仿真.

(责任编辑: 杨力军)