C语言程序设计递归算法的研究与应用

孙道层

（德宏职业学院 云南省芒市 678400）

1 前言

在C语言程序设计中，如果一个函数直接或者间接地调用自身，那么这种调用就被称之为递归调用，递归调用是嵌套调用的特例[1-2]。递归算法在程序设计中得到广泛的应用，通过函数递归的调用可以将非常复杂的问题转换为规模较小简单相似的问题，层层递进，最终求解[3]。函数递归算法策略大大减少程序的代码量，函数通过递归调用本身可以实现解决问题过程所需要的重复计算。研究C语言程序设计函数递归算法，有利于正确使用函数递归进行程序设计，降低程序运行的时间复杂度和空间复杂度，提高程序执行效率[4-5]。

2 函数递归算法的特征

函数递归调用本身时，会在计算机内部存储结构中开辟一个栈，对函数调用现场发起保护，并将函数调用时的参数和局部变量保存到新分配的存储空间，函数调用结束返回时，计算机会自动释放函数调用时存储的局部变量和参数所占用内部存储空间，弹出返回地址，继续执行调用函数语句的下一条语句。

例1 利用递归算法计算正整数m 的阶乘m！。程序代码如下

（1）每次函数递归调用，都会缩小问题的规模，并且为了防止无限期的递归调用，必须有结束递归调用的约束条件。例1 中当m 的值为1 时，ft=1,结束递归调用，当m＞1 时，发生递归调用，即在fact(m)函数中又调用fact(m-1),下面以3!为例，该函数递归的执行过程如图1所示。

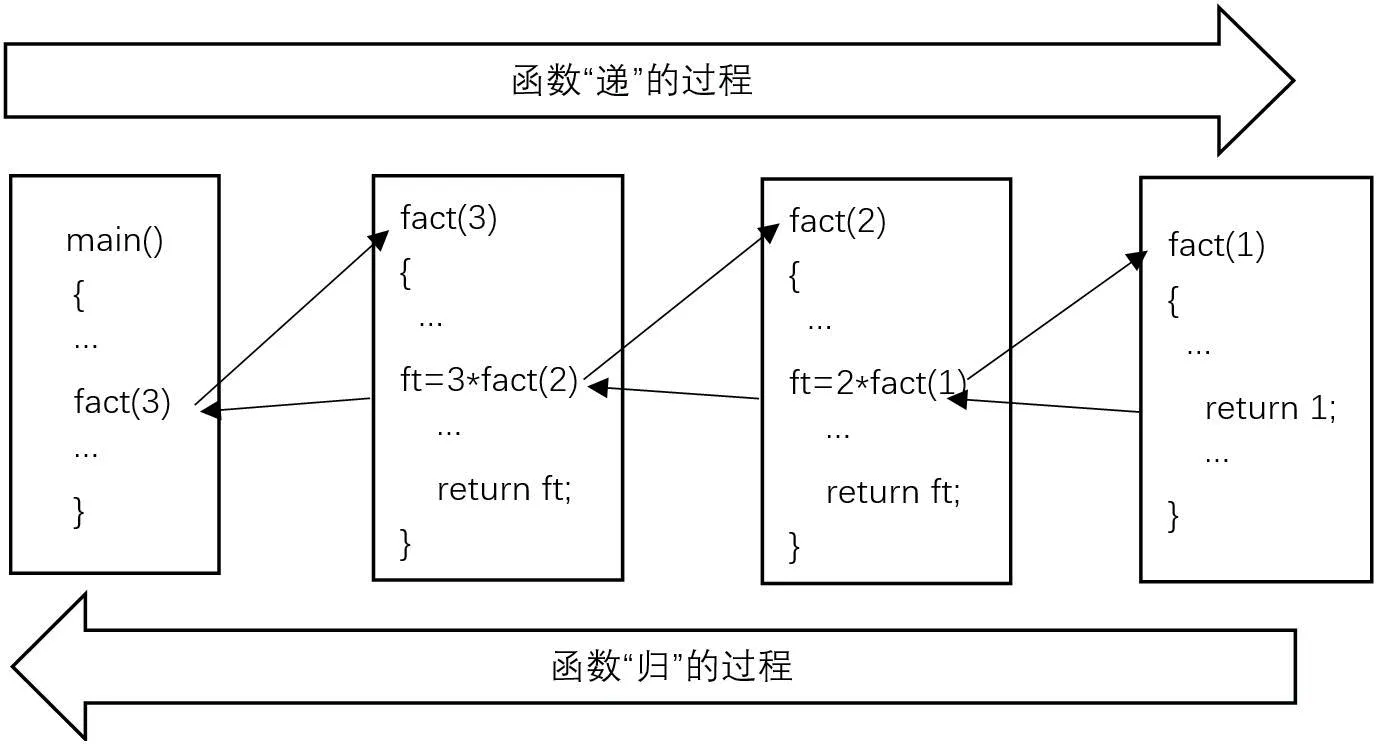
图1：函数的递归调用

通过3 次递归调用函数fact(m)来计算3 的阶乘。第一次调用fact(3),函数返回值ft=3* fact(2)，因为表达式含有fact(2)，需要调用函数本身fact(2)，只是这里函数参数已经变成2，问题的规模逐渐缩小，第二次调用结束后函数返回值为ft=2* fact(1)，最后以1为参数调用函数fact(m)时，函数返回值为1。最后一次调用函数结束后，返回调用fact(1)的地址，计算fact(2)= 2* fact(1)=2*1=2；继续返回调用fact(2)的地址，计算出fact(3)=3*fact(2)=3*2=6；最后返回到主函数调用fact(3)的地址，输出最终递归调用计算的结果。

在整个函数递归调用过程中，计算机内部存储结构使用栈保存函数调用的返回地址和参数值m，每次调用结束时，都按照栈中存储本次函数递归调用的返回地址返回到指定的位置继续执行，并且通过退栈操作，使得上次调用的参数成为新的栈顶继续被使用。

（2）函数递归调用特征就是每次调用后都必然使得原始问题规模缩小，并且子问题与原始问题相似，例1 中函数long fact (int m)的函数调用语句“ft=fact(m-1)*m;”就是使求解m 的阶乘的问题转化为求m-1 的阶乘问题，求解问题规模不断的缩小。

（3）递归算法实际求解问题中得到广泛的应用，有些类似的问题需要重复计算很多次，就必须使用递归算法才能很好的解决，设计递归算法的一般过程及终止递归的约束条件。比如二叉树遍历问题、皇后问题、汉诺塔问题等经典非数值的求解，应用递归算法是解决此类问题的最佳策略。

（4）使用递归算法编写程序，程序代码简洁明了，可读性强，代码冗余低，但是函数递归的调用，特别是数值计算类型的递归调用，需要占用大量计算机内部存储空间对函数多次递归调用的现场保护及参数保存，每次调用时和调用结束返回时都有入栈和出栈的操作，增加了程序运行的时间长度，因此递归调用增加了程序运行的时间和空间开销，降低了程序的执行效率。

3 函数递归的适用条件

使用函数递归算法应用非常广泛，正确地使用递归算法能够提高程序的可读性，降低代码冗余量，使用不当，会增加程序运行的时间和空间成本。寻找使用递归算法的适用场合就显得很有必要。首先要找出解决问题建立递归的关系，然后理出终止递归调用的约束条件。

能够使用递归解决问题，是否满足以下关系：

（1）建立递归关系；

（2）找出递归调用的终止条件；

（3）使用非递归算法实现极为困难，代码较为繁琐，可读性差，而使用递归算法编写的代码可读性强，简洁明了。

4 函数递归算法的应用

4.1 Hanoi塔问题

一板块上有三根针，即A，B，C。A 针上套有64 个大小不等的圆盘，大的在下，小的在上，要把这个64 个圆盘从A 针移到C针上，每次只能移动一个圆盘，移动可以借助B 针进行。但在任何时候，任何针上的圆盘都必须保持大盘在下，小盘在上。

Hanoi 塔问题设计算法如下：

设A 上有n 个盘子，如果n=1，则将圆盘从A 直接移到C。

如果n=2，则：

（1）将A 上的第一个圆盘移到B 上。

（2）再将A 上的第二个圆盘移到C 上。

（3）将B 上的一个圆盘移到C 上。

如果n=3，则：

（1）将A 上的前2 个圆盘借助于C 移到B 上，具体过程如下：将A 上的第一个圆盘移到C 上，再将A 上的第二个圆盘移到B 上，最后将C 上的一个圆盘移到B 上，此步骤再重复n=2 圆盘移动全过程。

（2）将A 上的剩下的圆盘移到C 上。

（3）将B 上两个圆盘借助于A 移到C 上，具体过程如下：将B 上的第一个圆盘移到A 上，再将B 上的第二个圆盘移到C 上，最后将A 上一个圆盘移到C 上。相当于第三步又完全重复当n=2的圆盘移动全过程。

从上面分析可以看出，当n 大于等于2 时，圆盘移动的过程可以分解为3 个步骤：

第一，把A 上的n-1 个圆盘借助于C 移到B 上。

第二、把A 上第n 个圆盘移到C 上。

第三、把B 上的n-1 个圆盘借助于A 移到C 上。

第一步和第三步分解为类同的三步，即把n-1 个圆盘从一个针上借助于第三个针移到另一个针上，这里把n-1 赋值给n，每次移动，n 的值递减一位，并且使用的方法完全一样，完全满足函数递归算法设计规则。

主要程序核心代码如下：

4.2 二叉树遍历

二叉树遍历分为三种方式，先序遍历、中序遍历、后序遍历，先序遍历访问的顺序是：根左右，中序遍历访问的顺序是：左根右，后序遍历访问的顺序是：左右根。下面以中序遍历为例，研究二叉树中序遍历的递归算法，中序遍历就是首先判断根结点的左子结点是否为空，为空则停止遍历，不为空将左子结点作为新的根结点重新进行上述判断，左子树遍历结束后，然后遍历访问该二叉树的根结点，并打印根结点，最后将根结点的右子结点作为新的根结点重新进行上述判断，直至遍历结束，到达每个结点时，打印该结点的数据，就可以得到二叉树中序遍历访问结果。二叉树如图2所示。

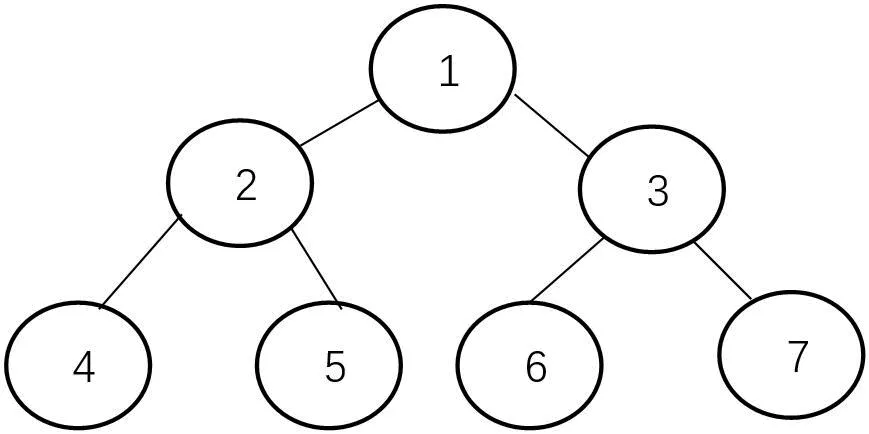
图2：二叉树

以图2 为例，二叉树中序遍历过程如下：

（1）首先访问该二叉树根结点，此二叉树根结点为1；遍历访问根结点1 的左子树，找到结点为2；遍历访问结点2 的左子树，找到结点4；由于结点4 没有左子树，因此找到结点4 后，遍历访问结点4 的右子树，由于结点4 无右子树，因此结点2 的左子树遍历完成，访问结点2 并打印该结点数据，遍历访问结点2 的右子树，找到结点5，结点5 没有左子树，因此访问结点5，又因为结点5没有右子树，因此结点1 左子树遍历完成。再访问二叉树的根结点1，并打印根结点1。

（2）访问结点1，并遍历结点1 的右子树，找到结点3，遍历结点3的左子树，找到结点6，由于结点6无左子树，因此访问结点6，又因为结点6 没有右子树，因此结点3 左子树遍历完成；开始访问结点3，并打印该结点数据，并遍历结点3 的右子树，找到结点7；由于结点7 无左子树，因此访问结点7，又因为结点7 无右子树，因此结点1 的右子树遍历完成，即整个二叉树遍历访问完成。

此二叉树的中序遍历是函数递归算法的典型应用，可以用C语言递归算法实现。核心代码如下：

5 结论

在C语言程序设中函数递归算法的应用比较普遍，函数递归算法设计程序，有利于程序代码简明可读性性增强，函数递归解决实际问题要注意问题本身是否适合建立递归关系的条件，如果满足建立递归关系的条件就可以使用递归算法求解，通过经典案例的应用，对函数递归算法应用执行进行详细的分析，有利于程序设计初学者更好理解递归算法的精髓，对程序开发者使用递归算法解决实际问题提供借鉴。