Discrepancies in surface temperature between NCEP reanalysis data and station observations over China and their implications

Ruihen Li , , Yu Hung , Fenghu Xie , Zunto Fu ,

a Laboratory for Climate and Ocean-Atmosphere Studies, Department of Atmospheric and Oceanic Sciences, School of Physics, Peking University, Beijing, China

b Department of Physics, Beijing Normal University, Beijing, China

c Department of Atmospheric Science, School of Environmental Studies, China University of Geosciences, Wuhan, China

Keywords:Irreversibility Reanalysis Evaluation Predictability Extreme events

ABSTRACT Previous studies show that temporal irreversibility (TI), as an important indicator of the nonlinearity of time series, is almost uniformly overestimated in the daily air temperature anomaly series over China in NCEP reanalysis data, as compared with station observations. Apart from this highly overestimated TI in the NCEP reanalysis,some other important atmospheric metrics, such as predictability and extreme events, might also be overestimated since there are close relations between nonlinearity and predictability/extreme events. In this study, these issues are fully addressed, i.e., intrinsic predictability, prediction skill, and the number of extreme events. The results show that intrinsic predictability, prediction skill, and the occurrence number of extreme events are also almost uniformly overestimated in the NCEP reanalysis daily minimum and maximum air temperature anomaly series over China. Furthermore, these overestimations of intrinsic predictability, prediction skill, and the number of extreme events are only weakly correlated with the overestimated TI, which indicates that the quality of the NCEP reanalysis should be carefully considered when conclusions on both predictability and extreme events are derived.

1. Introduction

Data quality is of vital importance in a range of fields, such as ecology, finance, and so on ( Bengtsson et al., 2004 ). In particular, a key approach in climate science is through data mining and analysis.There are different kinds of data, such as in-situ observations, gridded data, reanalysis data, and model outputs ( Bengtsson et al., 2004 ;Ma et al., 2008 ; Zhao et al., 2018 ; He and Zhao, 2018 ). One of the important concerns is the consistency among these different kinds of data. Evaluating their reliability plays an important role in related climate studies ( Bengtsson et al., 2004 ; Ma et al., 2008 ; Zhao et al., 2018 ;He and Zhao, 2018 ), such as climate trend estimation ( Bengtsson et al., 2004 ; Ma et al., 2008 ; Cornes and Jones, 2013 ), climate modeling ( Raghavenda et al., 2019 ), extreme climate and weather events( Rusticucci and Kousky, 2002 ; Flocas et al., 2005 ; Pitman and Perkins,2009 ; Hu et al., 2010 ; Mao et al., 2010 ; Cornes and Jones, 2013 ;You et al., 2011 , 2013 ; Zhu et al., 2017 ), and so on ( Yuan et al., 2013 ;Zhao et al., 2018 ; He and Zhao, 2018 ). Among them, numerous studies have attempted to assess the quality of reanalysis data by comparing with observations, since NCEP reanalysis data ( Kalnay et al., 1996 ;Kanamitsu et al., 2002 ) cannot always reproduce consistent results with observations ( Flocas et al., 2005 ). For example, a cold bias has been widely reported ( Ma et al., 2008 ).

Many earlier evaluation studies of reanalysis data mainly focused on the daily or monthly mean value of climate variables, such as mean air temperature ( T) and precipitation ( Bengtsson et al., 2004 ;Ma et al., 2008 ; Zhao et al., 2018 ; He and Zhao, 2018 ). Recently, interest has turned towards the assessment of extreme (maximum or minimum) air temperature (

T

or

T

) in reanalysis data ( Bengtsson et al.,2004 ; Ma et al., 2008 ; Zhao et al., 2018 ; He and Zhao, 2018 ), such as climate trend estimation, climate modeling, extreme climate and weather events, and so on ( Rusticucci and Kousky, 2002 ; Flocas et al., 2005 ;Pitman and Perkins, 2009 ; Mao et al., 2010 ; Cornes and Jones, 2013 ;You et al., 2011 , 2013 ; Zhu et al., 2017 ), since there are different behaviors between mean and extreme air temperature. It has been reported that there are different trends among

T

,

T

, and

T

( Karl et al., 1991 , 1993 ; Weber et al., 1994 ; Zhai and Pan, 2003 ). Evaluating the quality of reanalysis data can be carried out in different ways,including climatology comparisons, trend analysis, and probability density functions, from global to regional scales. All these evaluation methods involve global- and long-term-averaged climatological features. Actually, apart from these climatological features, more series-based features can be taken as an assessment index. For example, long-range correlation ( Yuan and Fu, 2014 ; Zhao et al., 2018 ; He and Zhao, 2018 )was taken as an assessment index to evaluate reanalysis data ( Zhao et al., 2018 ; He and Zhao, 2018 ). Previous studies have shown that the time series irreversibility (TI) is an intrinsic property ( Bartos and Janos,2005 ; Ashkenazy et al., 2008 ; Xie et al., 2016, 2019a ; Fu et al., 2016 ) of some measurements in meteorological fields. For example, it was found that rapid cooling and gradual warming are predominant in daily air temperature variations ( Ashkenazy et al., 2008 ; Xie et al., 2016, 2019a ;Fu et al., 2016 ). Also, this kind of TI has been taken as an evaluation index to assess the quality of NCEP reanalysis temperature data over China, including daily mean temperature, daily maximum temperature,and daily minimum temperature ( Xie et al., 2019a ). Contrary to the good TI consistency in

T

between reanalysis and observations, there is an almost uniformly high overestimation of TI in

T

and

T

( Xie et al., 2019a ). Since the dominance of TI is only found in motions on scales smaller than one month (actually, it is smaller than 15 days and mostly related to synoptic events ( Xie et al., 2016 )), previous globaland long-term-average assessment studies smoothed offthis feature. Together with this highly overestimated TI, might there also be other similar overestimations in NCEP reanalysis data? If so, is there any relation between them?

In climate and weather studies, extreme events and predictability( Huang and Fu, 2019 ; Fu et al., 2019 ; Xie et al., 2019b ) are two important and active research areas. At the same time, it has been reported that increasing nonlinearity could enhance the predictability( Ye and Hsieh, 2008 ; Huang and Fu, 2019 ). Therefore, together with the highly overestimated TI, the predictability and extreme events might also be overestimated. Accordingly, in this study, we focus on the nearsurface values of maximum and minimum temperature in the observations of 179 stations ( Li et al., 2009 ) and their corresponding interpolated NCEP R2 data (time span for both is from 1979 to 2016( Kanamitsu et al., 2002 )), which have been shown to perform well in previous studies ( Xie et al., 2016, 2019a ). We address the abovementioned questions from the following three perspectives: (1) the intrinsic predictability quantified by time series permutation entropy ( Huang and Fu, 2019 ; Fu et al., 2019 ); (2) the potential predictability or prediction skill measured by the ratio of low-frequency variance to total variance( Xie et al., 2019b ); and (3) the occurrence number of extreme events above certain thresholds.

2. Methods

All results presented in this paper are based on time series analysis. For ease of comparison, all series were normalized by subtracting their climatological annual cycle and dividing by the standard deviation. The normalized air temperature series for a representative station(Hangzhou (30.14°N, 120.10°E)) is shown in Fig. 1 , where both in-situ observations and interpolated NCEP data are shown for direct comparison (the interpolation method is described in detail in Xie et al. (2019a) ).

For each given series, the TI ( Xie et al., 2016, 2019a ; Fu et al., 2016 )can be quantified by

where

p

(

k

) and

p

(

k

) are the probability distribution function for the ingoing degree

k

(

t

) and outgoing degree

k

(

t

) in directed horizontal visibility graphs ( Luque et al., 2009 ) by mapping each series to a graph( Lacasa et al., 2008 ) through the horizontal visibility graph algorithm.For any series of given data length, the calculated value of

L

can be taken as the index to differentiate series from a reversible process to an irreversible one at the 95% confidence level, and the critical threshold of

L

is 0.0459 for series of the same length as the analyzed series in this study ( Xie et al., 2019a ).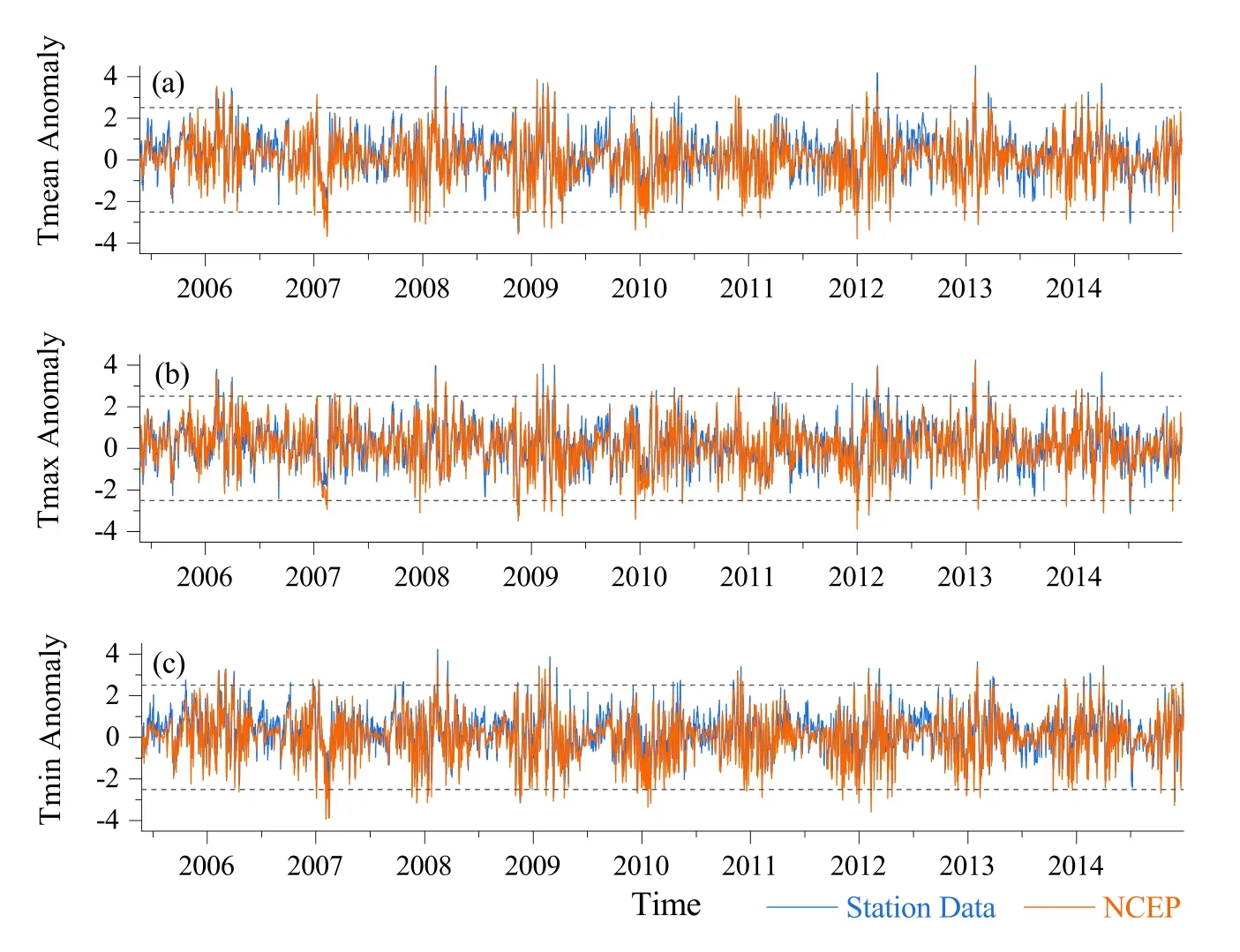

Fig. 1. Comparison of normalized temperature anomaly series between observations and interpolated NCEP reanalysis from a representative station (Hangzhou(30.14°N, 120.10°E)): (a) mean air temperature; (b) maximum air temperature; (c) minimum air temperature. Dashed lines denote ± 2.5 standard deviations.

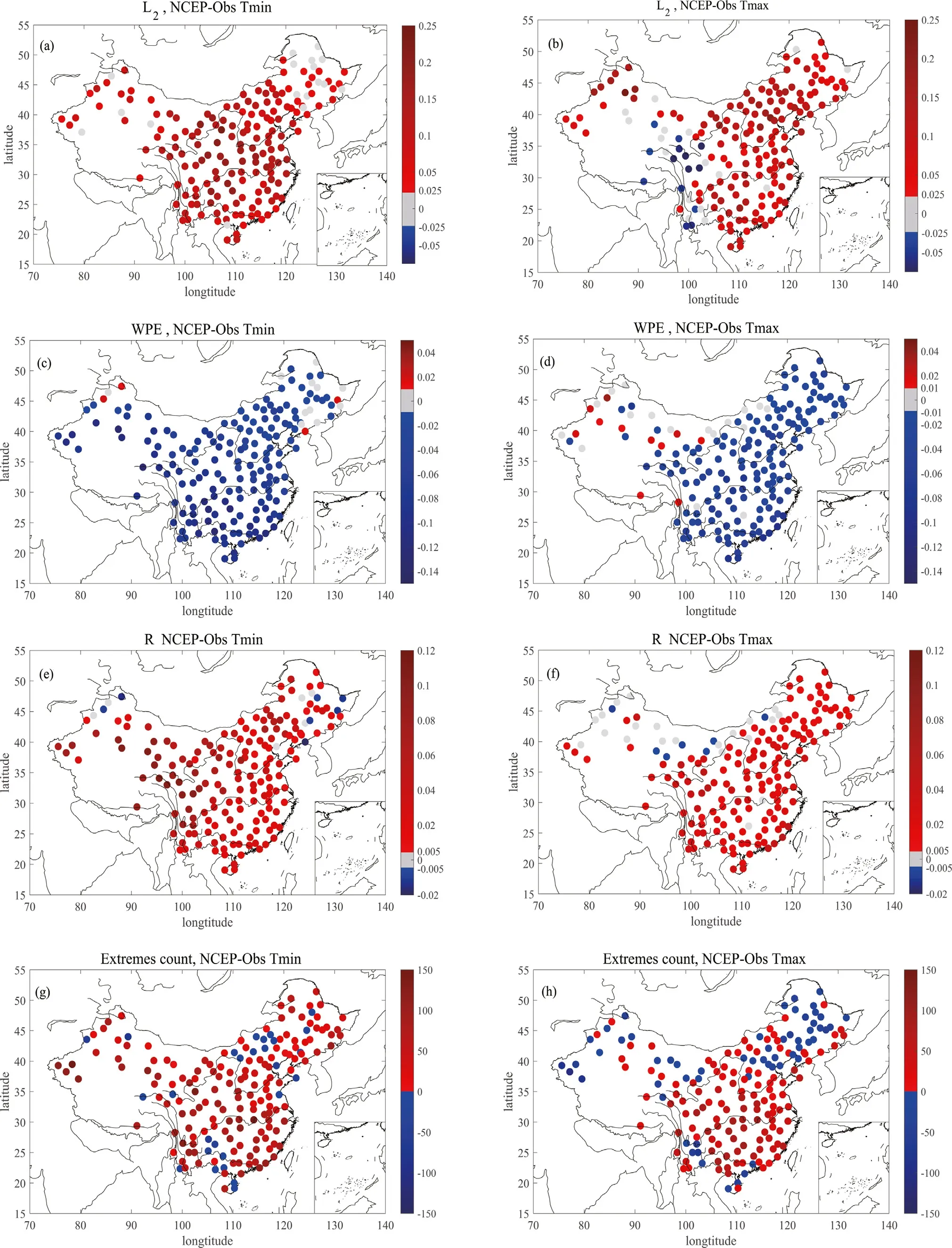
Fig. 2. Spatial distribution of four statistical differences between observations and interpolated NCEP reanalysis for minimum air temperature (left) and maximum air temperature (right): (a, b) temporal irreversibility quantifier L 2 ; (c, d) weighted permutation entropy WPE; (e, f) the ratio for low-frequency to total variance R ;(g, h) the numbers for extreme events’ magnitude larger than 2.5 standard deviations.

The marked TI differences for

T

and

T

between station observations and interpolated NCEP data are summarized in Fig. 2 (a,b). Over most stations (173/179 for

T

, 158/179 for

T

), the TI is overestimated. Especially for

T

, the TI is almost uniformly overestimated(most are statistically significant at the 0.05 level). Over the central parts of China (from 100°E to 120°E), this overestimation is even more marked (see Fig. 2 (a)). Therefore, in the next section, the main analysis and discussions will be focused on

T

.

Apart from this overestimated TI, three other aspects will be considered in this study. The first is the intrinsic predictability of time series quantified by means of weighted-permutation entropy (WPE)( Huang and Fu, 2019 ; Fu et al., 2019 ), defined as

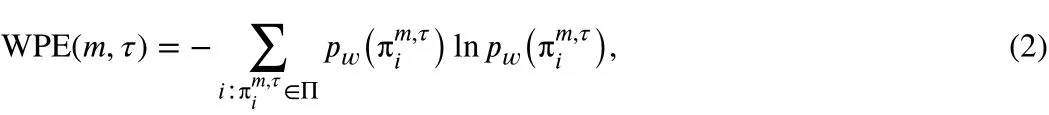
For any given time series, its potential predictability or prediction skill quantified by the variance ratio can be defined as ( Xie et al., 2019b )

with the time series decomposed by Fourier transform as

x

(

t

) =

x

(

t

) +

x

(

t

) , where

x

(

t

) and

x

(

t

) are its low-frequency and fast-varying part,and

V

(

x

) and

V

(

x

) are the low-frequency and total variance. The higher the value of

R

, the better the potential predictability of the underlying series.

Since extreme events are one of the hot topics in weather and climate studies, the third aspect will be the occurrence numbers for any given threshold, which can be defined as

where

σ

(

x

) is the standard deviation of time series

x

(

t

) and

λ

is any given constant. As previous studies have shown, the surface air temperature anomaly over the midlatitudes usually follows a normal distribution ( Bartos and Janosi, 2005 ; Ashkenazy et al., 2008 ). In this study, we set

λ

= 2

.

5 , which corresponds to the 99th or 1st percentile threshold for extreme events in most climate studies (a different choice of

λ

does not qualitatively alter the conclusions given in this study). Therefore, the higher the value of

N

, the greater the number of extreme events. Since the most important step in studying extreme weather and climate is to determine the extreme events, to reach consistent occurrence numbers for any given threshold from both the NCEP reanalysis and station observations is crucial to advance the study of extreme weather and climate,such as trend calculations of extreme events.

3. Results

3.1. Intrinsic predictability

Previous studies ( Ye and Hsieh, 2008 ; Huang and Fu, 2019 ;Fu et al., 2019 ) suggested that increasing nonlinearity in time series could enhance the intrinsic predictability. Here, the intrinsic predictability can be defined as 1-WPE ( Huang and Fu, 2019 ; Fu et al., 2019 ), where the lower the WPE, the higher the estimation of the intrinsic predictability in the interpolated NCEP data. Just as we found in the TI results, the WPE is overestimated over most stations (169/179 for

T

, 161/179 for

T

). The spatial patterns of WPE are highly correlated with those of TI (figure not shown here) for both station observations and the interpolated NCEP data, with a spatial Pearson correlation coefficient of− 0.573 for the interpolated NCEP

T

. The results in Fig. 2 (c,d) confirm that almost uniformly overestimated WPE in

T

also exists, especially over the central parts of China (from 100°E to 120°E).

3.2. Prediction skill

By Fourier decomposition and synthesis, we can differentiate the contributions of the low-frequency parts from those of fast-varying parts.For the analyzed data given in this study, there are 13870 data points in total for each series, and at most there can be 6935 harmonics. We summarized all the lower-order harmonics to represent the low-frequency contributions, and Fig. 2 (e,f) shows the results from the first 1700 harmonics (the results are insensitive to the choice of cut-offfrequency, and there is no qualitative difference from the 1700th to the 2200th harmonics; figures not shown here). It is clear that the potential predictability is markedly overestimated in the interpolated NCEP data, and for 166 of 179 stations for

T

and 162 of 179 stations for

T

the potential predictability

R

is overestimated. This is just as we expected since there is very high correlation (not linear but monotonic) between the intrinsic and potential predictability. The spatial correlation between the intrinsic predictability 1-WPE and potential predictability

R

over China is high for both station observations and the interpolated NCEP data;the Pearson correlation coefficient is 0.932 for station observations and 0.925 for the interpolated NCEP data of

T

.

3.3. Extreme events

Extreme events are important issues in weather and climate studies,and many previous studies were based on NCEP reanalysis data. Here,we check whether the abovementioned overestimation can be revealed in the estimation of the occurrence numbers of extreme events in

T

and

T

from the NCEP reanalysis compared with station observations.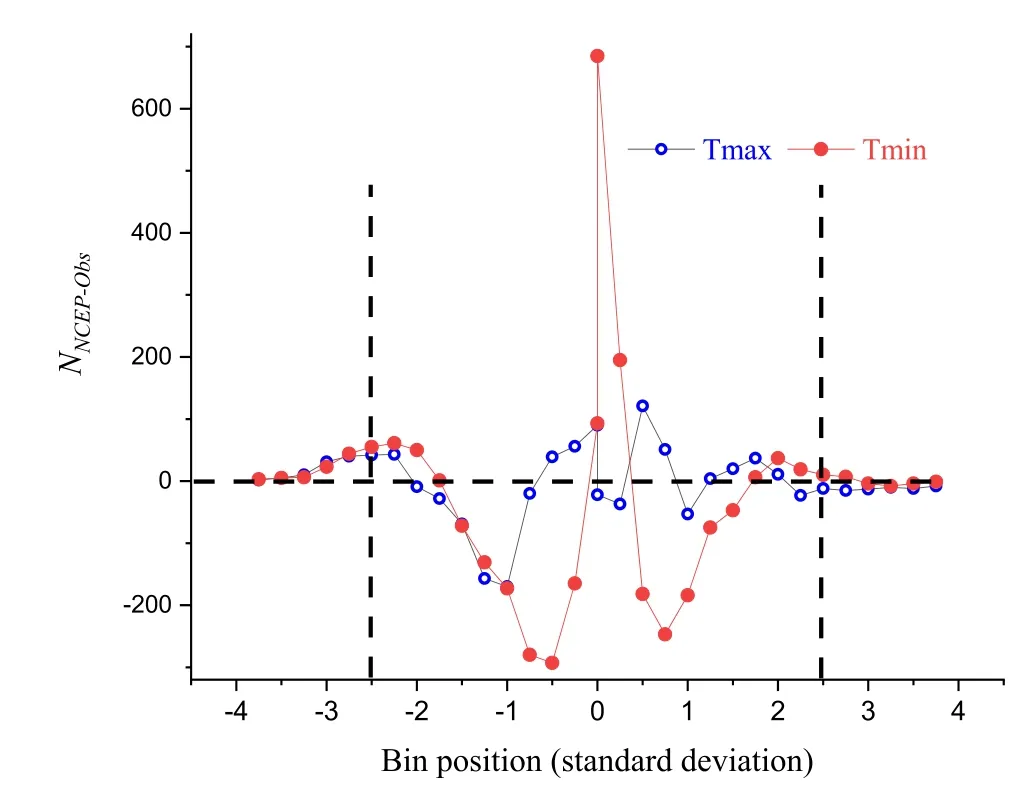

Fig. 3. Bin-averaged difference in the number of temperature events within a given interval between observations and interpolated NCEP reanalysis from a representative station (Hangzhou (30.14°N, 120.10°E)), where blue circles represent minimum air temperature and red dots maximum air temperature.Vertical dashed lines denote the position of ± 2.5 standard deviations and the horizontal dashed line represents zero difference.

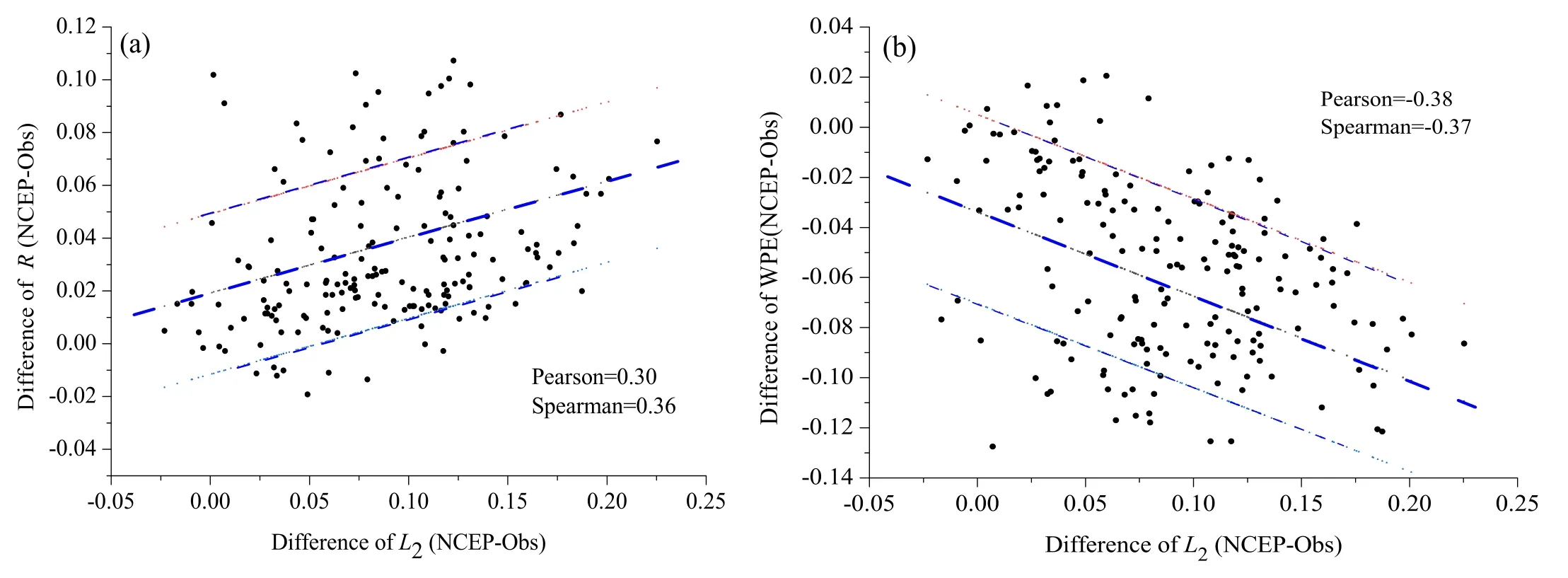
Fig. 4. Scatterplots of the (a) difference of R and (b) difference of WPE versus the difference of L 2 between observations and interpolated NCEP reanalysis for minimum air temperature anomaly series. Blue dashed lines are a visual guide for the linear fit, with the darker one for linear fit and the lighter ones representing the departure of one standard deviation.

For simplicity, we only consider the occurrence numbers of extreme events in the normalized series. Compared to the worse performance on predictability, the overestimation on the occurrence numbers of extreme events is not so serious. Only for 150 out of 179 stations for

T

and 117 of 179 for

T

are the occurrence numbers of extreme events over the whole span overestimated. At the same time, the spatial distribution for the difference in the occurrence numbers of extreme events above 2.5 standard deviations is also not so uniformly overestimated compared with those for predictability and TI (see Fig. 2 (g,h)). Further calculations indicate that the overestimated numbers of extreme events mainly occur for cold extreme events (see Fig. 3 ). Furthermore,this finding is consistent with the reported cold bias found in the NCEP temperature reanalysis, where it was reported that the NCEP reanalysis modeled colder winter temperatures than observations ( Ma et al., 2008 ).The colder bias in NCEP

T

and

T

can be also easily found in their series (see Fig. 1 (b,c)), where cold extreme events larger than 2.5 standard deviations can only be found in the NCEP reanalysis rather than in station observations.

4. Discussion and conclusions

The good degree of correlation in the spatial distributions of TI, predictability, and occurrence numbers of extreme events, together with their consistent overestimation, indicates that the overestimated TI may correlate with our calculated statistics from the NCEP reanalysis, which can be further confirmed by the scatterplots between the difference in TI and the difference in predictability quantifiers (see Fig. 4 (a,b)). However, there is only weak linear correlation between the difference in TI and the difference in WPE or

R

, and the Pearson and Spearman correlation coefficients give similar results around the value of 0.3. This fact indicates that TI is not the only factor to contribute to the overestimation of predictability in NCEP extreme air temperatures.Just as we mentioned in the above sections, assessment of reanalysis data in the literature has mainly focused on climatologies or trends; the considered time scales are larger than at least one month. Fewer studies have been devoted to the evaluation of synoptic events in reanalysis data. TI was reported to be able to mainly reflect synoptic events (less than half a month, and most within a week ( Xie et al., 2016 )) and the TI is highly uniformly overestimated in NCEP reanalysis extreme air temperature,

T

and

T

. From the variance ratio analysis, we found the cut-offfrequency band corresponds to the interval from the 1700th to the 2200th harmonics, and the time scale is around a week (from around 6 days to 8 days). This finding further confirms that the overestimated TI in NCEP reanalysis extreme air temperature might be closely related to synoptic events.

Together with the almost uniformly overestimated TI, the overestimation was only evaluated in NCEP extreme temperatures over China.Two related issues that should be considered in future research are:(1) whether similar results could be found in NCEP extreme temperatures over other regions of the world, and if so what the mechanism behind this overestimation might be; and (2) there are many reanalysis products besides the NCEP reanalysis, such as ERA-40, ERA-Interim( Ma et al., 2008 ) etc., and so would similar results found in this study also be revealed in other reanalysis datasets? Since there are different numerical models, assimilation systems, spatial resolutions, and so on in these reanalysis products, comparisons of TI, predictability, and extreme events among these different reanalysis products may be helpful in answering why there are overestimations in reanalysis products. For example, the observation-minus-reanalysis (OMR) method has been widely used to estimate the impact of land-surface forcing on surface temperature by computing the difference in trends between the reanalysis and observations, since the basis of the OMR method is that the observed surface temperature, moisture and wind over the land are not used in the NCEP reanalysis ( Hu et al., 2010 ). Finally, we should mention that all overestimations reported in this study are not from the interpolation(see Fig. S1). Revealing the detail of the mechanisms behind these overestimations and comparisons among different reanalysis products are required in future in-depth studies in these respects.

Declaration of Competing Interest

No potential conflict of interest was reported by the authors.

Funding

This research was funded by the National Natural Science Foundation of China [grant numbers 41475048 , 41675049 , and 41705041 ].

Supplementary materials

Supplementary material associated with this article can be found, in the online version, at doi: 10.1016/j.aosl.2020.100008 .