应用混合效应法建立的杂种落叶松人工林单木冠幅预测模型1)

马爱云 李凤日 董利虎

(东北林业大学，哈尔滨，150040)

树冠是树木的重要组成部分，它决定着树木的生活力和生产力。在树木生长过程中，树冠反映了树木长期竞争水平，是制定营林决策的重要树木变量[1-3]。冠幅是树冠研究中最常用的重要指标，可用来估计树冠的表面积与体积[4]、模拟树冠轮廓[5]、计算林木的竞争指数[6]等。此外，冠幅在林木生长与收获模型中常作为预测变量出现。因此，建立精准的冠幅预测模型具有重要意义。

目前常采用传统最小二乘法、哑变量方法以及线性和非线性混合效应模型方法等来构建冠幅预测模型[7-16]。Krajicek et al.[10]认为冠幅与胸径呈线性关系，在一定范围内，冠幅随胸径的增长而增大[10]；符利勇等[11]研究表明，基于Logistic、Richards非线性且具有生物学意义的理论模型能够更好地描述冠幅与胸径关系[12]；雷相东等[7]以落叶松云冷杉林为研究对象，采用多元逐步回归方法建立了9个树种的单木冠幅预测模型；张树森等[8]通过将胸径划分为3个等级，并将这3个作为哑变量的方式建立疏开木冠幅模型。针对不同地区不同树种，冠幅模型已经从普通最小二乘法建模发展到采用线性或非线性混合效应方法进行建模，且冠幅预测模型的变量也从常用的单一变量胸径逐渐加入各种林木变量和林分变量。

杂种落叶松(Larixkaempferi(Lamb.) Carr×LarixolgensisHenry)是落叶松属中一个非常重要的速生树种，具有高产、优质、抗病虫害等特性，是我国东北地区的重要用材树种之一。当前，黑龙江省营造了大量的杂种落叶松示范林[13-17]。在杂种落叶松人工林后续的森林生产经营管理理论研究中，肖锐等[18]针对不同初植密度杂种落叶松幼龄林的林分动态进行了模拟，王涛等[19]研究了杂种落叶松人工林幼龄林的枯损，但针对杂种落叶松的冠幅预测模型研究还未见报道。为了探索杂种落叶松冠幅预测模型，本文以黑龙江省江山娇实验林场1998年营造的杂种落叶松林为研究对象，具体为日本与长白落叶松的杂交种，从7种常用的冠幅与胸径关系基础模型中挑选较好的模型来进一步研究杂种落叶松冠幅预测模型，分析了杂种落叶松冠幅与胸径及其他林木因子、林分因子的关系。最终将样地作为随机效应因子，构建杂种落叶松单木冠幅混合效应预测模型，为杂种落叶松人工林的可持续经营及动态模拟提供依据。

1 研究区概况

黑龙江省江山娇实验林场，地处黑龙江省东南部，在黑龙江省宁安市境内，地理坐标为东经128°53′16″～129°12′43″，北纬43°44′54″～43°54′12″。林场东南部与吉林省相接，西部以镜泊湖为界，整个施业区处于东京城林业局之中，位于张广才岭南端，东西走向，东高西低，北高南低，属于低山丘陵地区，海拔356～890 m。气候属亚寒带大陆性气候，年平均气温3.5 ℃，年平均降水500 mm。区域内主要林分类型为人工针叶林、阔叶混交林、针阔混交林和柞树林4类，主要树种有红松(Pinuskoraiensis)、云杉(Piceaasperata)、落叶松(Larixgmelini)、水曲柳(Fraxinusmandshurica)等10余种，森林覆盖率达95%。

2003年黑龙江省林业科学研究院以江山娇实验林场1998年种植的不同初植密度(2 500、3 300、4 400、6 600株/hm2)的杂种落叶松林为试验地，在各初值密度的杂种落叶松人工林设置12块固定样地，共计48块固定标准地，样地面积为0.03～0.06 hm2，各固定样地集中，立地条件基本相同，除一次轻微的人为修枝外，林分未进行过任何抚育间伐。2015年对48个样地进行每木检尺，用胸径尺测量距地面1.3 m处的树干直径，即胸径(DBH)，精确到0.1 cm，树高(H)和第一活枝高(HCB)用超声波测高器测量，精确到0.1 m，以样木树干为中心，用钢尺分别对其东、西、南、北4个方向的树冠半径进行测量，精确到0.1 m。根据东、西、南、北4个方向的树冠半径，计算树冠直径平均值即树木平均冠幅(CW)。除此之外，还计算了冠长率(CR)、高径比(HDR)、林分断面积(BAS)、优势木平均高(H0)、优势木平均胸径(Dg)、大于对象木的胸高断面积之和(BAL)等因子。48块杂种落叶松林的林分因子统计信息见表1。

表1 杂种落叶松林基本因子统计

2 研究方法

2.1 基础模型构建

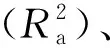
2.2 线性混合效应模型

在线性模型中，所有的参数都是固定效应参数，线性混合效应模型是线性模型的进一步扩展，既包含固定效应又包含随机效应，同时误差有更为灵活的结构，还可以改变随机效应的方差—协方差结构来反映个体间的差异[11-12，24，28，31-32]。本研究数据来自于不同初植密度的48块样地，为考虑样地对冠幅的随机干扰，以样地为随机效应因子，构建样地单水平线性混合模型，模型形式如下：

(1)

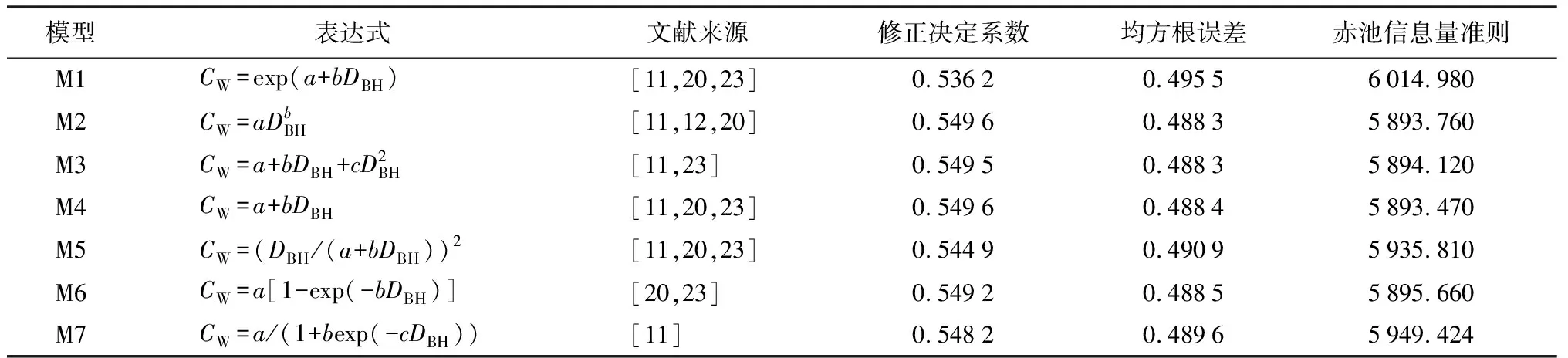
表2 冠幅基础模型

图1 冠幅—胸径相关关系

混合效应模型的构建，在R软件nlme包的lme模块中实现，模型的参数估计采用的是限制极大似然法(REML)。在未知随机效应矩阵的情况下，考虑所有参数都可能存在随机效应，对所有不同随机效应参数组合的模型都进行拟合，在收敛的模型中，通过比较赤池信息准则、贝叶斯信息准则和负2倍对数似然值来确定最优随机效应组合。对于随机效应的方差—协方差矩阵，本文采用常见的广义正定矩阵、复合对称和对角矩阵3种方差—协方差结构分别拟合，选择赤池信息准则、贝叶斯信息准则和负2倍的对数似然值最小的矩阵结构作为随机效应方差—协方差矩阵结构[21]。

2.3 模型的评价与检验指标

本研究采用修正决定系数、均方根误差、赤池信息准则、贝叶斯信息准则、负2倍的对数似然值等指标对模型的拟合优度进行评价比较，采用平均绝对偏差、平均相对偏差绝对值两个偏差统计量和模型拟合效率一个检验指标对模型进行检验[25-27]。赤池信息准则、贝叶斯信息准则和负2倍的对数似然值由R软件直接给出，其余指标计算公式如下。

(2)

均方根误差(RMSE)：

(3)

平均绝对偏差(MAE)：

(4)

平均相对偏差绝对值(MAPE)：

(5)

模拟效率(EF)：

(6)

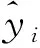
本文利用全部样本来构建冠幅混合效应模型，采用留一交叉验证法[24]进行模型检验，即每次取出一个样地数据作为检验样本，其余47个样地数据作为建模数据，如此共循环检验48次，计算48次检验结果的平均值来衡量模型的预测性能。对混合效应模型随机参数的检验采用经验线性无偏最优预测法(EBLUP)来计算随机效应参数值[24，27-28]。具体计算公式如下：

(7)

2.4 不同样本量对随机效应的校正

混合效应模型在应用时，对随机效应参数的估计是最为关键的，本研究在检验模型时，用了各样地所有样木冠幅实测值来计算随机效应参数，但在实际的森林资源调查中，要调查样地内所有的样木冠幅，是不切实际的，因此需要分析小量的样本对随机效应的校正精度的影响，确定较为合适的调查样本量。根据前人的研究表明，不同数量的样木对混合效应模型的预测有影响，预测偏差一般随样本量的增多而减小[29]，通常每个样地抽取样本量为4时，足以校正随机效应[30]，Xie et al.[24]的研究表明抽取接近样地优势木数量的6个样本量时较为合理。因此本研究中，基于上述的留一法，采用随机抽样，在没有替换的情况下，对每个样地分别抽取2、3、4、…、30棵树，分别重复抽取100次，组成不同抽样株数的子样本，用于计算各样本量下的随机效应参数，并得到混合模型对应的预测偏差，从而计算不同样本量下的检验统计量，进行对比分析，最终得到较合适的随机效应校正样本量。

以上所有的计算过程均在R软件4.0中实现，主要使用nlme包[25]。

3 结果与分析

3.1 模型的构建

3.1.1 单木因子与林分因子

基于选定的最优基础模型M4，采用再参数化的方法引入一些常用的单木因子和林分因子。具体做法如下：1)分样地拟合基础模型，得到各样地的模型参数；2)分析参数与单木因子和林分因子的相关性，确定β=f(x)的具体形式，其中β为模型中的参数，x为相关性强的单木因子和林分因子；3)将f(x)的具体形式代回到模型中。除此之外还需要求各变量在统计上显著(p<0.05),且自变量之间存在较弱的共线性(方差膨胀系数小于10)。再参数化构建的冠幅最优线性模型形式为：

CW=a0+a1DBH+a2CR+a3HDR+a4BAS。

(8)

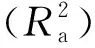
3.1.2 混合效应模型

CW=(a0+b0)+(a1+b1)DBH+a2CR+(a3+b3)HDR+

a4BAS。

(9)

表3 模型(8)在不同随机效应参数下的拟合比较

对模型(9)采用不同随机效应方差—协方差矩阵结构进行模拟，选择赤池信息准则、贝叶斯信息准则和负2倍对数似然值最小时的广义正定矩阵结构为协方差矩阵结构。

3.2 模型的评价与检验

图2 冠幅观测值与模型(8)、模型(9)的预测值相关图

表4 模型(8)与模型(9)的参数和随机效应方差估计

3.3 不同样本量对随机效应的校正对比

用不同抽样数量组成的子样本计算混合效应模型(9)的随机效应参数时，模型的预测效果见图4。其MAE和MAPE值整体上随着抽样数量的增大而减小，与模型拟合效率随着抽样株数量增大而增大的结果相符，说明增加计算随机效应参数的样本量，模型的预测精度会提高，这与前人的研究一致[24，29-30]。当样本量为5株及大于5株时，模型预测精度提高减缓，对不同样本量下的模型预测的误差进行显著性检验也表明，5株及更多的抽样株数之间没有显著差异，当样本量达到12株左右时，模型预估精度趋于稳定不变。

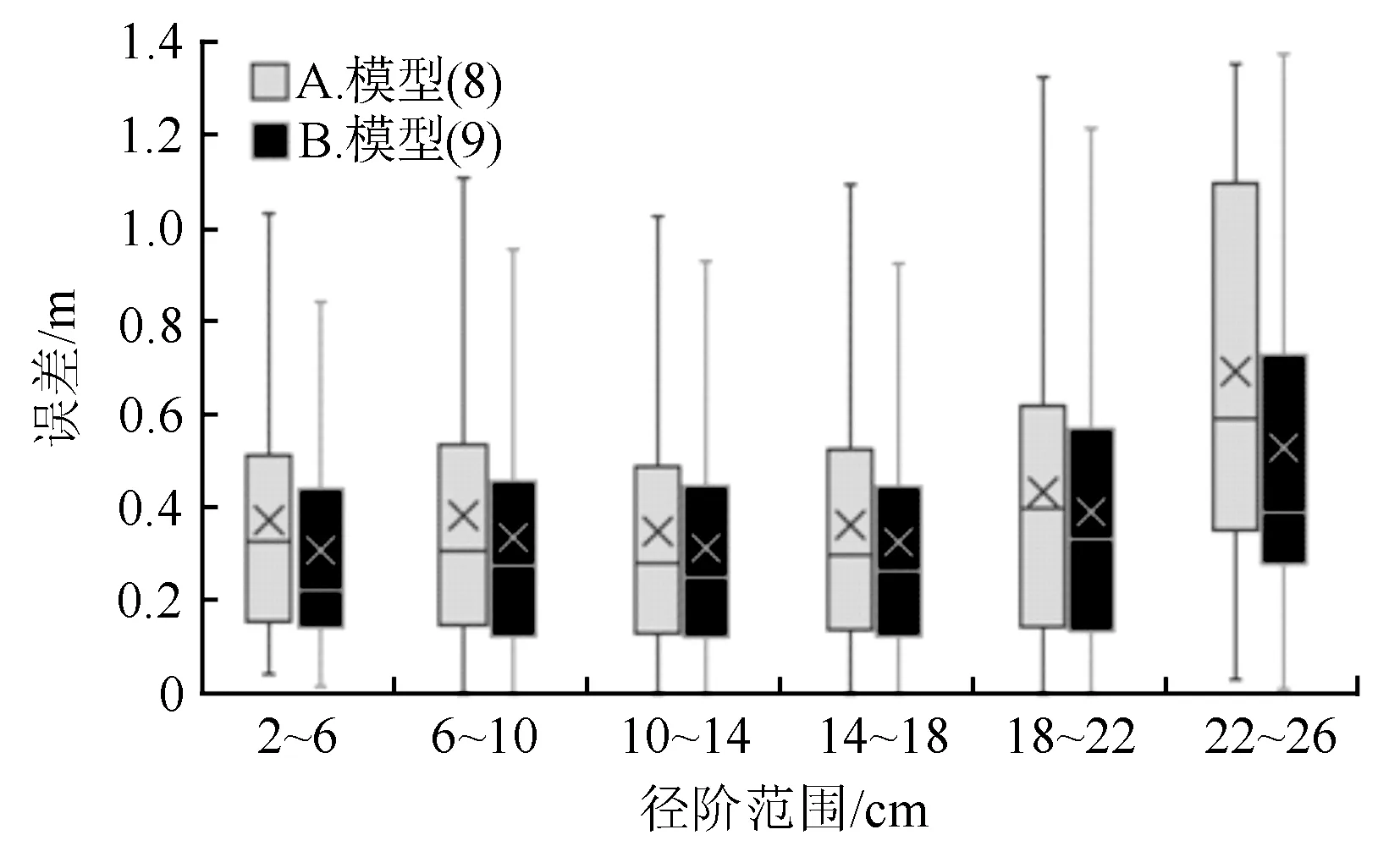
图3 不同径阶下模型(8)与模型(9)的预测误差分布图

表5 线性模型与混合效应模型检验结果

4 结论与讨论

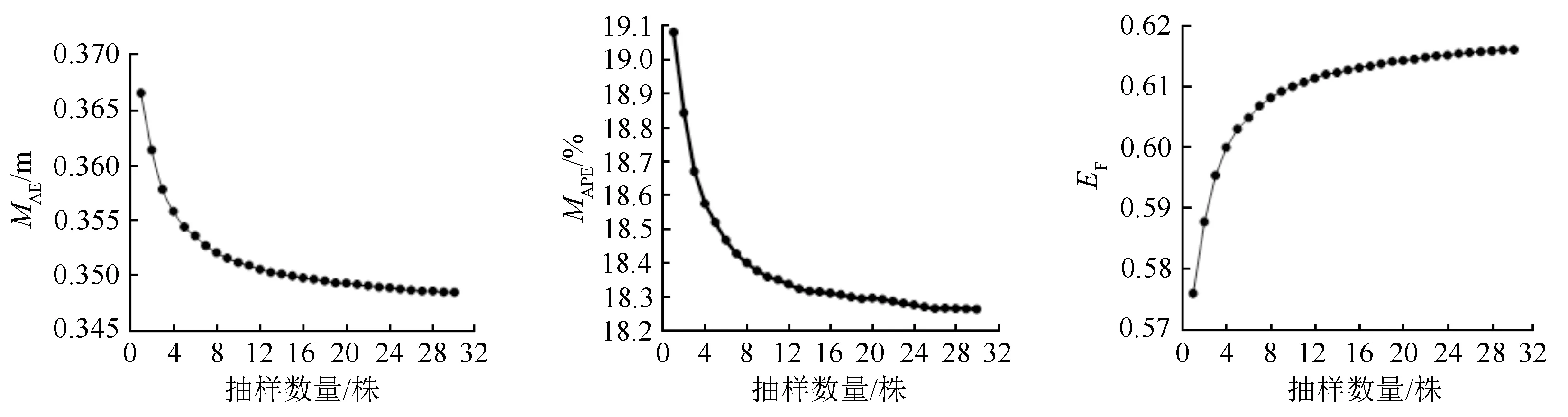
图4 不同抽样数量计算随机效应的预测精度变化

1)在变量DBH、CR和HDR上添加样地随机效应时，模型预测效果最佳，线性混合效应模型的拟合与检验结果均比最优线性模型好。本文比较了不同抽样株数对随机效应的校正，表明模型的预测效果随着样本数的增加而提高，在样本量为12及以上时，模型的预测指标趋于稳定不变，但当抽取株数为5及以上时，便没有显著性差异。因此，在应用该模型进行预测时，根据抽样调查成本和精度的要求，建议随机抽取接近样地优势木株数的5个样本即可，这与Xie et al.[24]的研究一致。

2)模型中，变量DBH和CR的参数均为正数，这与以往研究相符[12，23，32]，表明冠幅与DBH、CR呈正相关；变量HDR的参数为负，说明冠幅与HDR成负相关，这与前人的研究一致[20，23，32]；变量BAS的参数为负数，因为本研究数据来自于不同初植密度的林分，且林分年龄相同、立地质量相似，所以在林分株数密度较大时，林分断面积相对较大，此时的竞争也较大，从而导致冠幅较小，该变量以往很少被作为协变量加入冠幅预测模型，但在本研究中，变量BAS的加入具有一定的生物学意义和统计意义。

总之，本研究所构建的杂种落叶松单木冠幅线性混合效应模型有较好的预测精度，该模型对研究区域的杂种落叶松能进行较好的预测，且确定了每个样地抽取5个样本量即可校正随机效应参数，从而减少了森林资源调查中的成本，具有实际应用价值，为杂种落叶松林的经营管理提供了一定的依据。此外，该模型所选入的变量DBH和BAS在实际地面调查中较容易获取，变量CR和HDR需要调查林木树高，目前无人机雷达数据获取树高较方便，所以该模型有较好的实用性。但由于数据的局限性，对于其它区域的预测效果还需要进一步验证，在今后的研究中可基于多区域多林龄的林分进行研究，扩大模型的应用范围。