小波去噪在压力容器声发射检验中的应用

孙琼琼* 赵亚东 刘见向

（1.泰安市特种设备检验研究院 2.肥城市国家电网）

0 前言

近年来，随着经济不断发展，越来越多的压力容器被广泛应用于化工、机械、石油、军事等工业领域。压力容器是重要的承压类特种设备，在各工业领域发挥着至关重要的作用，同时压力容器也是一种危害性极大的特种设备，当其发生故障时会引起中毒、爆炸等事故，不仅对周围环境及人身安全造成重大威胁，甚至会造成重大经济损失[1]。因此定期对压力容器进行监测、检验，能对可能发生的缺陷、故障进行预报，从而保障压力容器安全运行。

声发射是指压力容器材料局部因应力引起的能量快速释放而产生应力波的现象，这种应力波按声波的规律传播，并携带了大量的材料内部结构信息，通过检测这种波并加以处理，可以发现压力容器的内部缺陷，为无损检测提供了可能[2]。在压力容器缺陷发展初期，其声发射信号强度很弱，且以振动信号的形式呈现，利用传感器将振动信号转换为电信号，并经过放大器放大后，由采集处理系统采集信号并上传，然后进行分析。

但是在压力容器检验现场，由于传播路径、耦合效果和传感器的响应对最后接收到的声发射信号都有影响，且其他各类设备及人员产生的噪声，使得传感器采集到的声发射信号严重失真，甚至淹没在噪声信号中，通过研究压力容器声发射信号采集过程中的去噪问题，可将含噪的声发射信号进行提纯，对后续灾害预警、保障安全生产具有重大意义。

1 小波变换理论基础

小波变换(Wavelet Transform)的基本思想是用一族函数去表示或逼近一信号或函数,这一族函数称之为小波函数系，其是由一基本小波函数平移和伸缩构成的[3]。

假设 ，连续小波变换即是将小波基或母小波 平移b，在不同尺度a 下与信号f（t）作内积运算，即：

式中：a ——尺度因子；

b ——平移因子。

2 小波阈值去噪理论

在小波阈值去噪过程中，影响去噪效果的4 个因素分别为小波基函数、分解层数、阈值和阈值函数。

2.1 小波基函数选取原则

小波基函数具有不唯一性，不同的小波基函数具有不同的时频特性，因此阈值去噪的效果也不同。所以，在工程应用中应结合待分析信号的特点，选择最合适的小波基函数，常用的小波基函数及性质如表1所示[4]。

表1 常用小波基函数的性质

2.2 分解层数选取原则

分解层数的选择会直接影响去噪效果，一般根据信号的实际情况选择分解层数。针对信噪比较高的信号，选择较小的分解层数就可将噪声与信号分离开；针对信噪比较低的信号，可利用较大的分解层数来抑制噪声。

2.3 阈值选取原则

在小波阈值去噪中需要设定一个合适的阈值，这个阈值将起到门限的作用，将信号中噪声和有用信号进行分离，常用的阈值包括以下4 种[5]。

（1） 无偏似然估计原则(rigrsure)

无偏似然估计原则是一种基于Stein 无偏似然估计原理的自适应阈值选择。对于给定的阈值T，得到它的似然估计值，再将似然T 最小化，就得到了所选的阈值，这是一种软件阈值估计方法。

（2） 通用阈值原则(sqtwlolg)

（3） 启发式阈值原则(heursure)

启发式阈值原则是无偏似然估计和固定阈值估计原则的折中。如果信噪比很小，按无偏似然估计原则处理的信号噪声较大，在这种情况下，就采用固定阈值形式。

（4） 极值阈值原则(minimax)

极值阈值原则采用极大极小值原理选择阈值，产生一个最小均方误差的极值，而不是没有误差。

2.4 阈值函数选取原则

在确定阈值后，通常选用软、硬阈值函数对小波系数进行处理。硬阈值法只保留大于阈值的小波系数并将其他的小波系数置零[6]。其表达式如下：

软阈值法将小于阈值的小波系数进行恒定收缩，否则置零，其表达式如下：

3 实践仿真

在压力容器检验现场采集纯净的声发射信号，如图1 所示，并加入10 dB 的高斯白噪声如图2 所示，结合该信号特点选用Symlets 小波作为分析声发射信号小波基函数，并进行4 层分解，通过不同的软硬阈值去噪方式进行去噪处理。

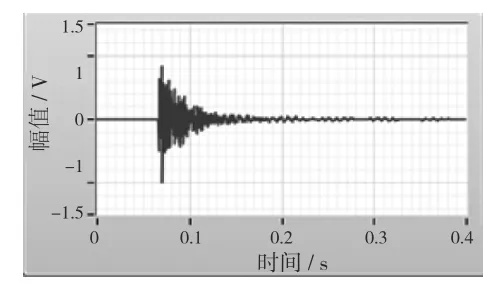
图1 纯净的声发射信号

图2 含噪的声发射信号

由图3，图4 可以看出，经过硬阈值方式进行去噪处理后，声发射信号产生了明显的伪吉普斯现象，形成振荡信号，经软阈值函数处理后的信号比较平滑，所以在工程应用中多采用软阈值去噪方式进行去噪处理。

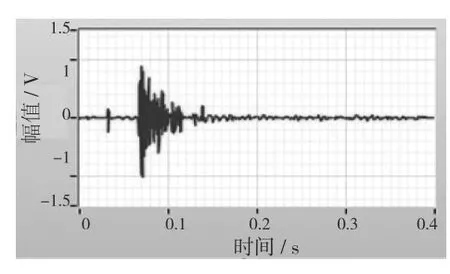
图3 硬阈值去噪

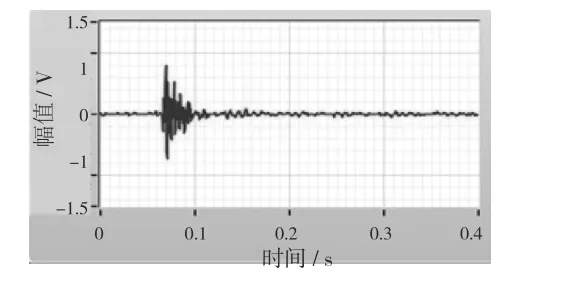
图4 软阈值去噪

4 结语

本文通过分析压力容器检验现场的声发射信号及噪声特点，从小波基函数、分解层数、阈值选取及阈值函数4 个方面深入分析了小波去噪在声发射信号中的应用。通过实验仿真，选用Symlets 小波基函数进行去噪处理，结果表明，软阈值去噪有较好的去噪效果，可广泛应用于工程实践。