三维流线追踪截短偏置超声速尾喷管非设计工况性能分析①
鲁广钊,周 帅,张 帅,郑 耀
(1.浙江大学 航空航天学院,杭州 310027;2.中国航空发动机研究院,北京 100074)
0 引言
超燃冲压发动机不需要携带氧化剂且能提供较大的比冲,相比于传统火箭发动机是更适合高超声速飞行器的动力解决方案[1]。尾喷管是超燃冲压发动机中提供推力的主要部件,非对称喷管可以把飞机后体作为膨胀面的一部分使用,适合与机身进行一体化设计。尾喷管在多种情况下的工作性能影响到高超声速发动机的性能,研究尾喷管在非工况情况下的性能对于设计高超声速飞行器使其在较宽的飞行范围内保持高性能有重要意义。
常用的高超声速尾喷管设计方法是基于特征线法(MOC)[2]提出的最短长度设计方法(MLN)[3]设计给定长度的二维单斜面膨胀喷管(SERN),目前国内外针对SERN已存在大量研究[4-8],二维单斜面膨胀喷管拓展到三维情况下需要指定侧向扩张角、斜切角等[9],这导致喷管实际流场结果受到侧向膨胀影响无法在整个流场中符合设计情况。本实验室的付磊[10-11]运用最短长度理论以及非线性截短方法[12]设计了轴对称喷管,通过数值模拟得到流场,再以该流场为基准采用流线追踪[13]的方式在偏离流场轴线处取圆形进口,提取流线,进行拟合得到偏置尾喷管。通过截短设计后得到的尾喷管整体长度更短易于发动机的装配,偏置设计可以使喷管产生俯仰力矩,易于与飞行器进气道及整体力矩配平。本实验室的朱美军[14]在设计过程中针对非线性截短过程引入了优化,在一定长度范围内保证了喷管最优的推力性能和升力性能。该类尾喷管的一大特点是在俯仰方向有不对称性,推力及推力矢量在不同的状态下变化对飞行器的性能有较大的影响,因而对其非工况性能的研究有重要意义,目前对该类喷管非工况性能的研究较少。本文将针对该尾喷管展开非工况条件下性能的研究分析,为三维非对称高超声速尾喷管的性能分析以及飞行器发动机设计提供参考。
1 设计方法
截短偏置高超声速尾喷管的设计流程如图1所示[15]。首先确定基准流场,采用特征线法求解流场,得到轴对称最短长度喷管,然后指定压比PR(喷管出口压力与外流压力之比),当气体在喷管内膨胀到一定压力后,从尾部对其进行截短,另一方面运用非线性截短方法[11]进一步缩短其长度。采用CFD数值模拟得到截短轴对称喷管的流场。再以得到的轴对称喷管的流场作为基准流场,在该流场进口偏离流场轴线一定位置处取封闭曲线,通过该封闭曲线上的点采用流线追踪技术,提取流场中的流线,将得到的流线进行曲面拟合,得到偏置后的三维喷管造型。最后,考虑壁面的边界层效应,对设计的外形进行边界层修正[16]。设计过程中以偏置尾喷管的升力和推力为优化目标,对轴对称尾喷管的截短过程进行了优化,生成得到截短偏置超声速喷管。

图1 三维非对称喷管设计流程
1.1 最短长度喷管(MLN)设计方法
假设喷管内流动为稳态、无黏、无旋、等熵的超声速流动,求解的方程为双曲型偏微分方程组,即式(1)。采用特征线法求解该方程组,有限差分方法计算该方程组的特征线方程和相容性方程[2]。
(1)
如图2所示,最短长度喷管的流场由核心流区(OAB区),变向流区(ABC区)和均匀流区(BCE区)组成。核心流区为是膨胀波发生的区域,决定了下壁面的长度;变向区为简单波发生区域,该区域内采用质量守恒原理确定上壁面的形状[11];在均匀流区流场的马赫数达到设计要求并保证流场均匀性。

图2 最短长度喷管的设计示意图
1.2 流线截短设计方法
使用最短喷管理论设计得到的理想最短长度喷管后部有很长一段壁面的斜率较小,对推力的贡献很小,而气体在进入喷管进口处最初膨胀区域膨胀剧烈且压力大,贡献了绝大部分喷管的推力。非线性截短设计保留最初的膨胀区域,截短对推力贡献小的尾部区域,这样可以最大保留喷管的推力性能,同时极大地减小喷管长度,使其更满足实际应用的要求[12]。
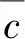
(2)
保持喷管轴向高度不变,型面由缩短因子函数生成,即对于喷管纵向界面上某一点(x,y)有压缩后的坐标(x′ ,y′ ),其中
(3)
本文选用的非线性缩短因子函数表达式如下:
(4)
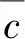
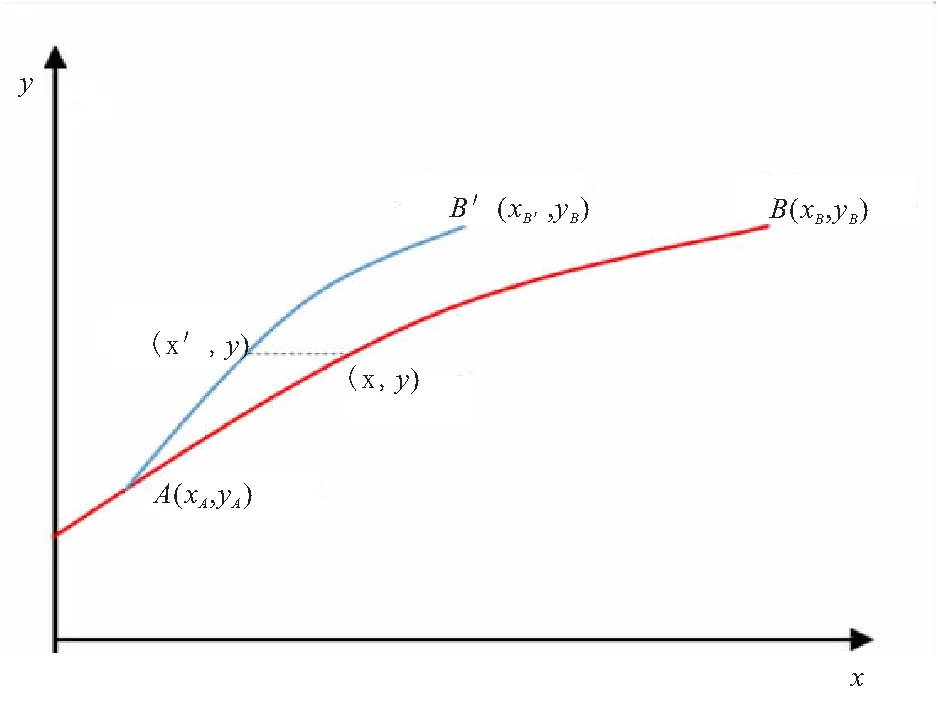
图3 尾喷管的非线性压缩过程
1.3 基于代理模型的尾喷管优化
为获得性能最优的截短尾喷管,对尾喷管进行基于代理模型的优化设计。三维非对称截短尾喷管的基于代理模型优化的流程示意如图4所示[14]。

PR∈[1.5,3.5,5.5,7.5]
A∈[0.1,0.2,0.3,0.4]

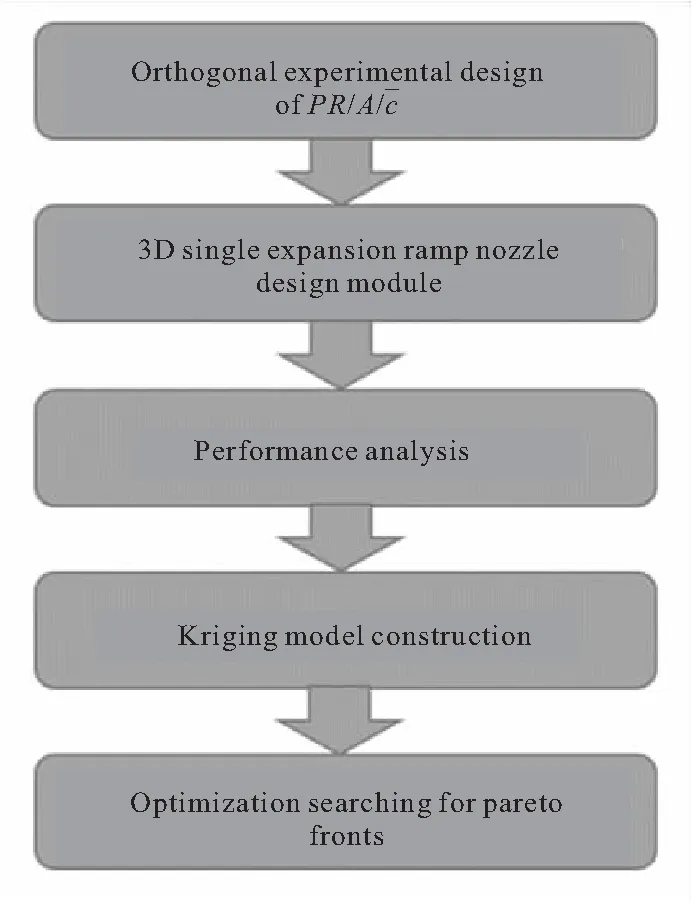
图4 基于代理模型优化的流程示意图
尾喷管的代理模型选用Kriging 模型,多目标优化选择NSGA2 算法。算法中最初的种群数目为40,迭代步数为700 步,交叉率为0.9。推力Fx和升力Fy为优化目标,可以通过数值模拟结果得到。三个设计变量分别在各自的范围内变化,尾喷管长度作为一个约束变量,这样可以避免喷管长度过长或过短。优化问题可以表述如式(5):
(5)
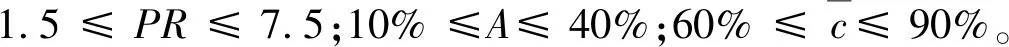
本文尾喷管选取设计工况参数如表1所示。
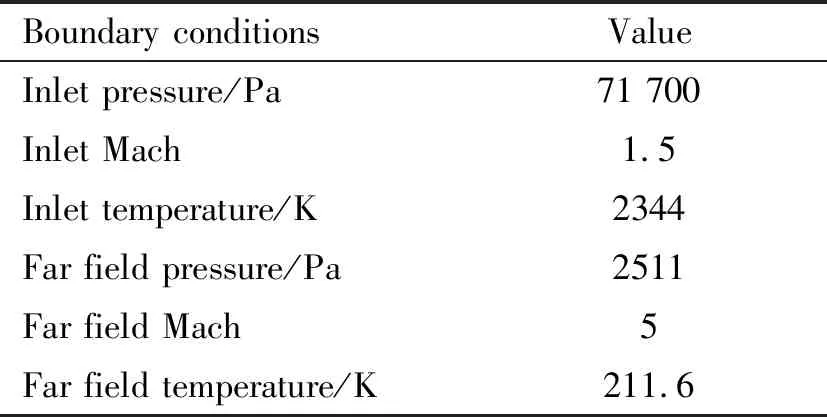
表1 尾喷管设计工况参数
设计构型几何参数进口为直径12 cm的圆,偏置距离圆心2.5 cm,经过优化,喷管长度为0.736 m,设计推力为352.44 N,设计升力为69.47 N。尾喷管三维外形如图5所示。

图5 尾喷管三维构型
2 数值验证
采用商业软件Pointwise和Fluent分别对造型好的尾喷管进行网格生成和数值求解。为简化计算规模,根据尾喷管的几何面对称特性,只采用一半的计算域,如图6所示。

图6 计算网格分布
尾喷管壁面网格用前沿推进法设置,控制壁面y+<1,经计算,壁面第一层网格高度选为1×10-6m,尾流部分采用加密处理。定义压力远场、压力出口、壁面和对称面等边界条件。采用隐式定常的时间积分格式和基于密度的求解算法,选取二阶AUSM格式和SSTk-ω两方程湍流模型及理想气体模型进行数值模拟。设计三套网格,网格数分别为1 500 000,2 000 000和2 500 000。图7为网格无关性验证结果,图中显示的曲线为喷管上下壁面压力系数分布,可以看到网格在中等网格密度时,即2 000 000网格时达到收敛,为提高计算效率,同时保证计算精度,选取中等密度网格进行数值模拟。

图7 网格无关性验证
设计工况参数如表1所示,根据该组数据模拟得到的流场三维马赫数等值线如图8所示。通过马赫数等值线图可以观察管内膨胀波系,如图中虚线所示。流场结构与设计基准流场结构相符。计算出喷管的推力为346.30 N,升力结果为71.82 N,与优化设计的结果能够较好符合。

图8 设计工况下尾喷管对称面流场马赫数等值线图
3 结果与讨论
3.1 进口参数对喷管性能的影响
3.1.1 尾喷管进口压力改变情况
尾喷管进口压力受到进气道与燃烧室影响,若是进气道和燃烧室工作不稳定,会导致尾喷管进口压力的变化。选取尾喷管进口压力分别为60 000、 65 000、70 000、75 000、80 000 Pa,其他进出口边界条件和表1中所示保持相同。尾喷管推力,升力以及俯仰力矩大小随进口压力变化曲线如图9、图10所示,随着进口压力增大,尾喷管的压差推力和黏性阻力均在增大,但是黏性阻力增长的幅度并没有压差推力增长的幅度大,因而总推力的大小随着进口压强的增长而不断增大,且呈近似线性。
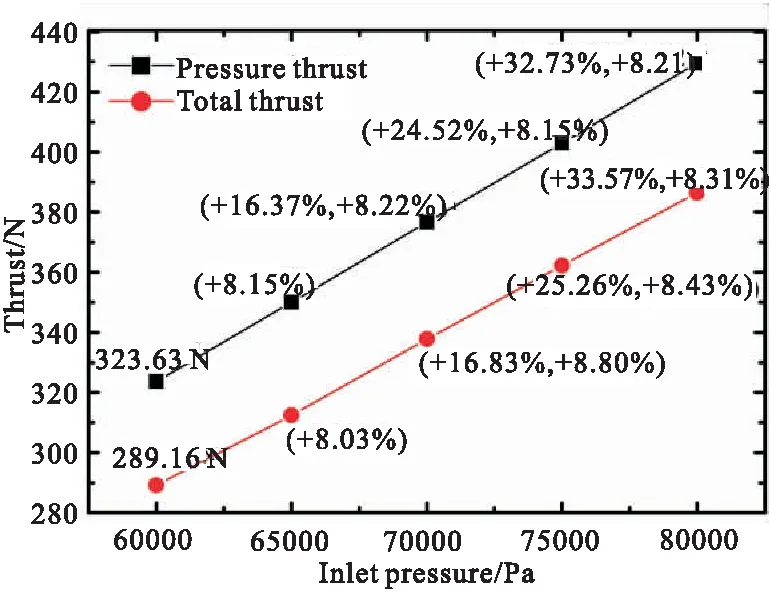
*The first percentage in the bracket is the ratio of the paramater at current pressure with the parameter at 60 000 Pa;the second percentage in the bracket is the ratio of the parameter with the pervious parameter.

*The first percentage in the bracket is the ratio of the paramater at current pressure with the parameter at 60 000 Pa;the second percentage in the bracket is the ratio of the parameter with the pervious parameter.
从图9中数据看到,进口压力每增大5000 Pa,压差推力和总推力增大8%左右。俯仰力矩的计算矩点取尾喷管圆形进口的圆心位置,尾喷管的升力和俯仰力矩随着进口压力的增大呈近似线性增长,进口压力每增大5000 Pa,尾喷管升力和俯仰力矩增大8%左右。推力升力和俯仰力矩的变化与进口压力的变化呈近似等比例关系。
气流进入尾喷管后发生膨胀,马赫数增大,压力减小。图11为变入口压力情况下喷管内气体压力分布。喷管所受到的力来源于气体在喷管内膨胀后对壁面施加的压力所产生的合力,由图11中喷管内部压力分布可知,随进口压强增大,喷管内气体膨胀后作用于喷管壁面的压力增大,因而气体通过压力作用于喷管壁面的合力增大,于是喷管推力增大。

图11 变进口压力喷管对称面内压强等值线分布图
随着进口压力的变化,尾喷管进口气体质量流量发生变化,表2给出了尾喷管比推力、膨胀比和总压恢复系数随进口压力变化数据。可以看到,随着进口压力的变化,尾喷管的比推力几乎不变。随着进口压力增大,尾喷管膨胀比增大,总压恢复增大。虽然黏性阻力增大,但是黏性阻力造成的总压损失增大程度小于总的总压恢复增大程度,因而总压恢复系数也是增大的。
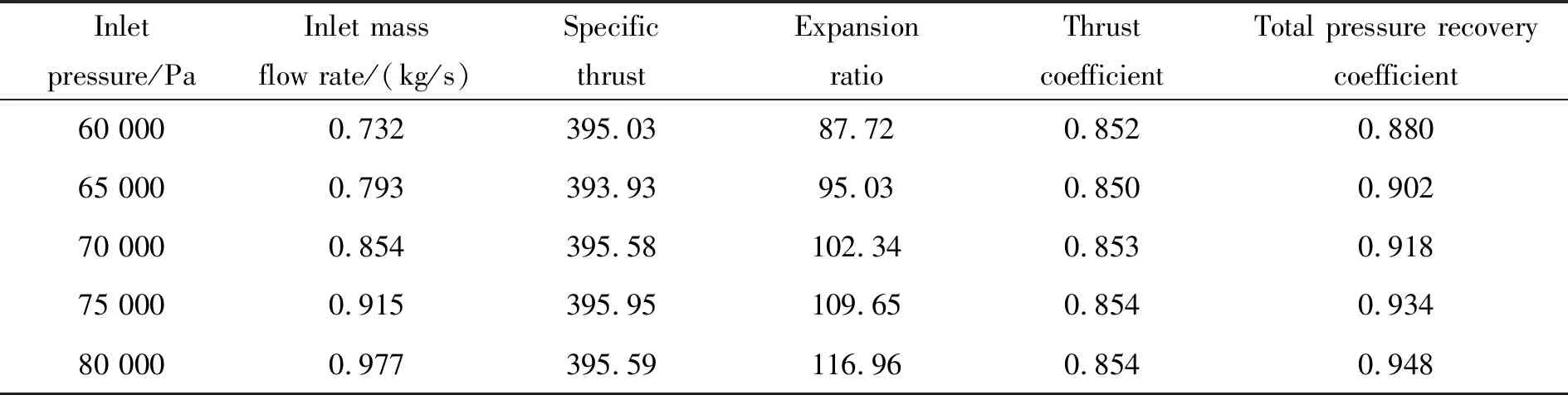
表2 变进口压力时尾喷管的比推力、膨胀比和总压恢复系数
3.1.2 尾喷管进口马赫数对喷管性能的影响
模拟分析尾喷管进口马赫数的改变对尾喷管性能的影响。保持尾喷管进口温度、压力以及外流温度、压力和马赫数和表1一致,改变进口马赫数分别为1.0、1.2、1.4、1.6、1.8和2,尾喷管推力、升力和俯仰力矩变化曲线如图12和图13中所示。

图12 尾喷管推力随进口马赫数变化曲线

图13 升力和俯仰随进口马赫数变化曲线
随着进口气体马赫数增长,黏性阻力增大。但是黏性阻力增长的幅度并没有压差推力增长的幅度大,因而总推力的大小随着进口马赫数的增长而不断增大。
从图12和图13可以看到,随着进口马赫数增大,尾喷管推力和俯仰力矩的增长有减缓趋势。从图13可以看到,尾喷管的升力随进口马赫数的增大而先增大后减小。
6种情况下,尾喷管内对称面的压力从入口71 700 Pa降低到7000 Pa时的压力分布等值线图如图14所示。从图14可以看到,随着进口马赫数增大,喷管内整体的高压范围(>7000 Pa)增大,喷管内受到气体压力作用的合力更大,喷管推力增大。 空气对喷管下壁面压力作用增长的速度比上壁面更快,导致喷管升力先增大后减小。随着进口马赫数的增长,尾喷管升力合力的作用点向后移,且幅度较大,导致尾喷管的俯仰力矩始终增大。
表3为尾喷管比推力、膨胀比和总压恢复系数随进口马赫数的变化数据。可以看到,尾喷管的比推力和推力系数随着进口马赫数增大而增大。喷管进口总压随着尾喷管进口马赫数增大而不断增大,因而膨胀比也增大。总压恢复系数随着尾喷管进口马赫数增大而增大。
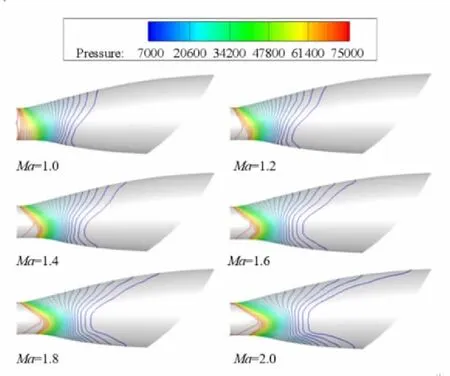
图14 变进口马赫数喷管对称面内压强分布图

表3 变进口马赫数时尾喷管的比推力、膨胀比和总压恢复系数
3.2 外流参数对尾喷管性能影响
3.2.1 外流马赫数改变情况
变外流马赫数在4~7.5范围内变化,其他边界条件如表1中选取,共有8种情况:外流马赫数分别为4,4.5,5,5.5,6,6.5,7,7.5。图15为选取了外流马赫数为4、5、6、7的情况下流场对称截面马赫数等值线分布图。可以看到,在尾喷管的出口尾流处,喷管内的流动与外流存在较大的速度差,因而形成了强烈的剪切层。外流马赫数越大,内外流层的速度差越大,剪切层越强烈。
表4给出了变外流马赫数情况下尾喷管的推力和升力变化数据。喷管受到的力和力矩来源于气体在喷管内膨胀的产生的压力,从图15中看到超声速上游影响下游,外流马赫数的改变并没有使尾喷管内部流场波系发生显著变化,因而从表4中可以看到,改变外流马赫数对尾喷管推力、升力和俯仰力矩的性能并没有显著性影响。相较于各参数平均值,压差推力变化最大幅度为0.17%,黏性阻力变化最大幅度为2.6%,总推力变化最大幅度为0.40%,升力变化最大幅度为0.94%,俯仰力矩变化最大幅度为0.40%。考虑计算误差,尾喷管的推力、升力以及俯仰力矩随着外流马赫数的变化而几乎不产生变化。外流的马赫数大小并不是影响尾喷管性能的主要因素。但是从飞行器整体设计的角度来说,外流马赫数会影响飞行器尾部的流场结构,从而影响飞行器的整体性能。
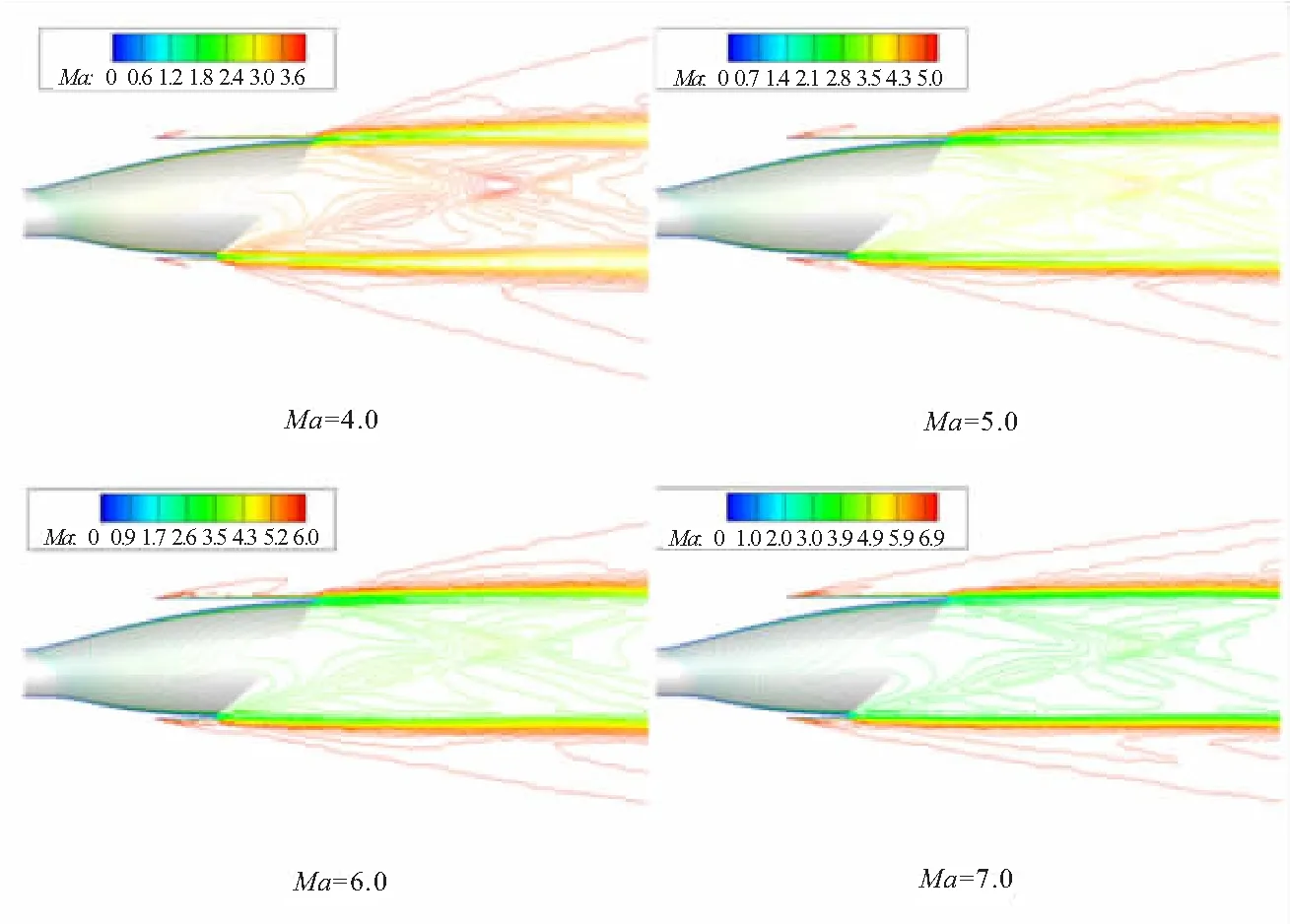
图15 变外流马赫数情况下尾喷管对称面流场马赫数等值线图
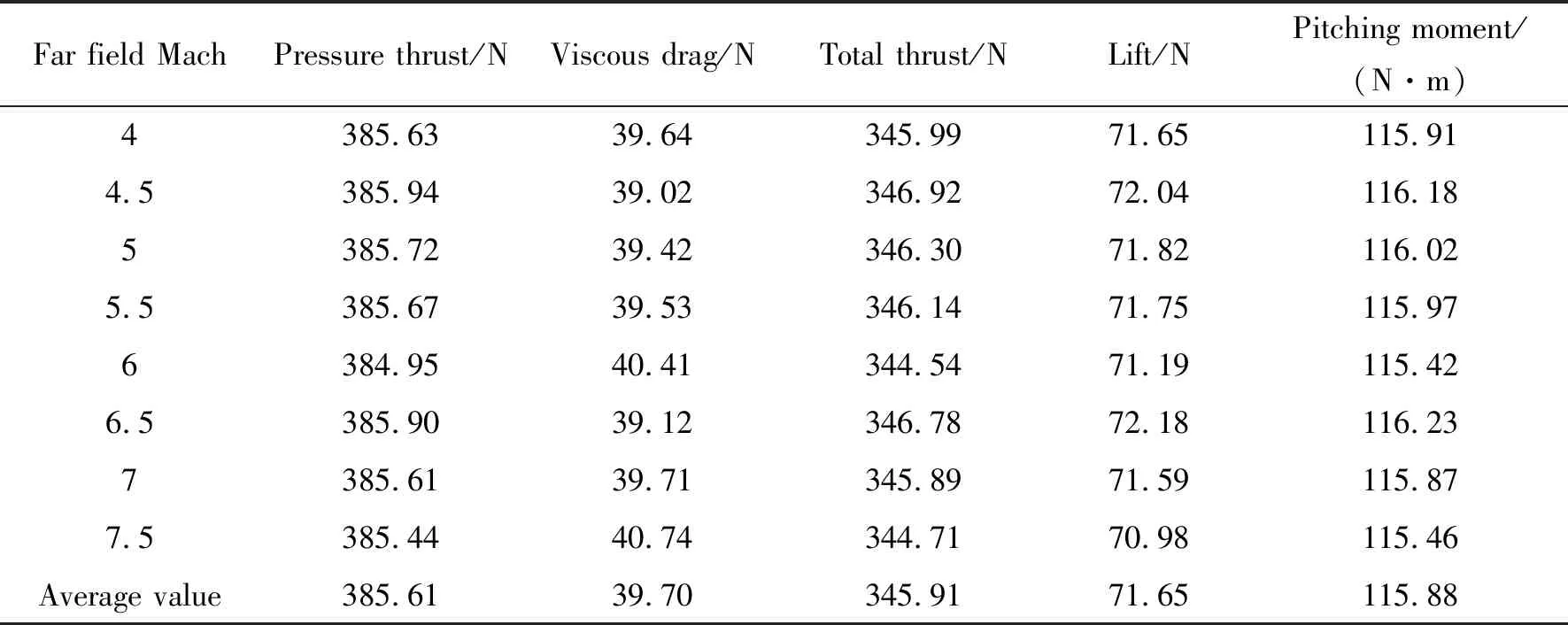
表4 变外流马赫数时尾喷管的推力和升力
3.2.2 飞行高度改变情况
对照1976标准大气参数表,控制飞行器飞行高度在10 000~25 000 m之间,如表5所示,共选择了6个算例。可以看到,根据高度不同,尾喷管出口的外流压力和温度也不同,改变喷管外流温度和压力如表5中所示,其他边界条件和表1一致,讨论不同飞行高度情况下,尾喷管的性能。

表5 不同高度大气参数
由表5可以看到,随着高度变化,温度的变化并不大,但是外流压力变化较大,随着高度增加,外流压力不断变小。尾喷管尾部的流场结构受外流压力影响发生变化,给出6种情况下,尾喷管对称面流场马赫数等值线图,如图16所示。
不同高度情况下,膨胀比如表6中所示。在低高度情况下,由于外流压力较大,设计工况膨胀比大于实际膨胀比,入口总压不变的情况下,气体在喷管内膨胀后到尾喷管唇口处的压力小于外流压力,出现过膨胀现象,此时会出现激波,激波导致外流气体向内膨胀。在此处剪切层有向内收缩的趋势,在膨胀区域内外流气体马赫数变大,气流经过尾流区域的激波后发生转折。随着高度的升高,外流压力逐渐变小,在尾喷管唇口处剪切层由内缩逐渐转变为水平,表明流场从过膨胀状态逐渐变为完全膨胀和欠膨胀状态。
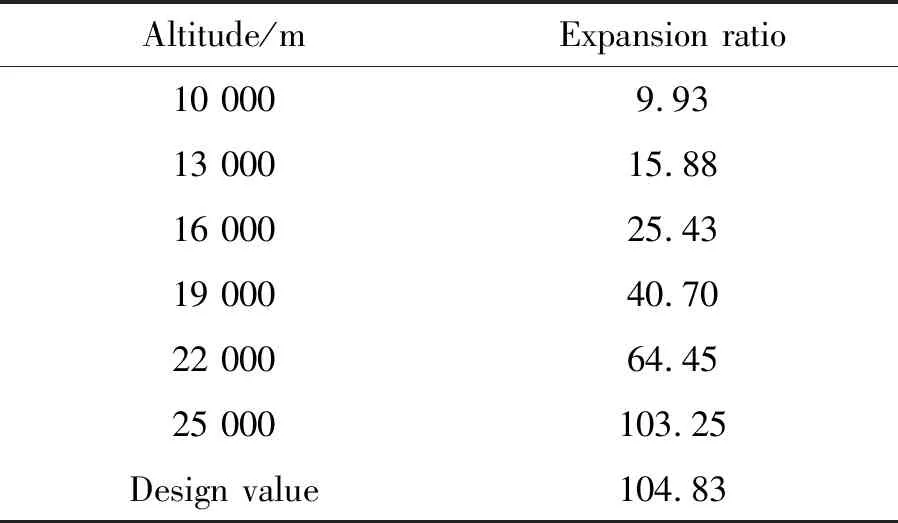
表6 尾喷管不同高度情况下膨胀比

图16 变飞行高度情况下尾喷管对称面流场马赫数等值线图
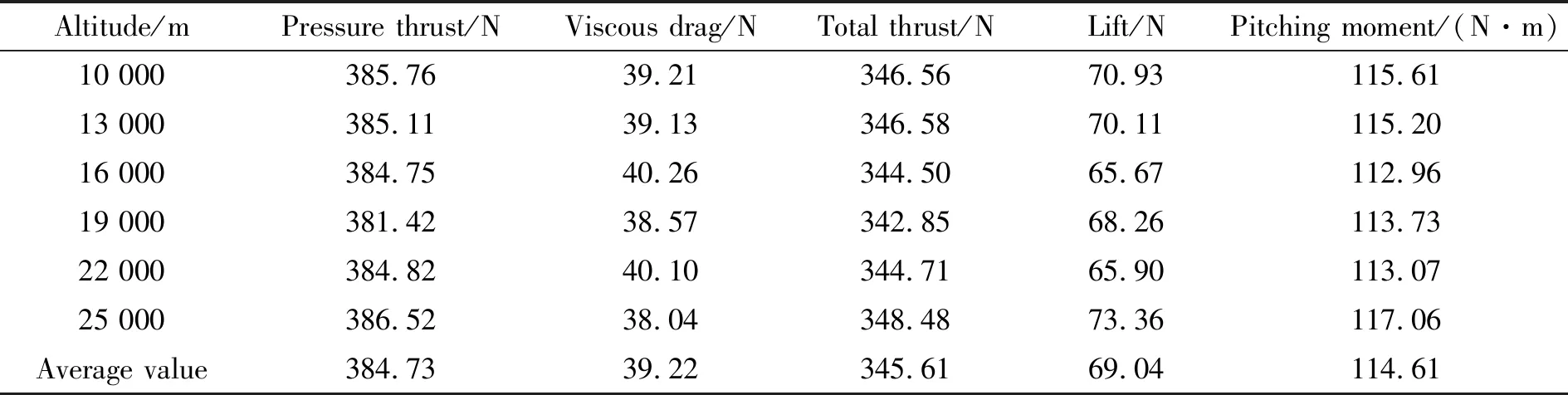
表7 变飞行高度时尾喷管的推力、升力和俯仰力矩
表7为变飞行高度时尾喷管的推力和升力变化数据。从表中可以看到,相较于各参数平均值,压差推力变化最大幅度为0.86%,黏性阻力变化最大幅度为3.0%,总推力变化最大幅度为0.83%,升力变化最大幅度为6.2%,俯仰力矩变化最大幅度为2.1%。从流场马赫数等值线图16可以看到,外流压力的变化对喷管尾部流场结构影响很大,但是喷管内部超声速上游影响下游,外流压力和温度的改变对内部流场并不产生影响,因而尾喷管性能参数变化不大。
4 结论
本文采用最短长度喷管设计方法(MLN),非线性截短方法以及基于代理模型的优化方法设计了三维截短偏置高超声速尾喷管,并针对该尾喷管变入口马赫数、变入口压力、变飞行高度和变外流马赫数等情况,采用数值模拟展开了非工况情况下的分析。结论如下:
(1)外流参数变化对尾喷管出口流场结构产生较大影响,对尾喷管内部流场不产生影响,对喷管的性能产生微小影响。外流马赫数越大,内外流之间的剪切越强烈;改变飞行高度,会明显改变外流压强,在外流低压情况下,唇口处出现欠膨胀现象;而在外流高压情况下出现过膨胀现象,此时唇口处出现激波,外流气体会在尾喷管唇口处向内膨胀。
(2)内流参数改变对尾喷管的性能变化较大。超声速尾喷管的推力和升力与尾喷管内的膨胀范围大小有关。随着尾喷管进口马赫数增大,尾喷管的推力不断增大,尾喷管的升力和比推力先增大后减小,尾喷管的推力系数增大。随着尾喷管进口压力增大,尾喷管的推力和升力以及俯仰力矩增大,每增大5000 Pa入口压强,尾喷管的推力、升力和俯仰力矩增大8%左右,与进口压力的增长呈近似等比例关系。尾喷管的比推力和推力系数并没有出现明显变化。尾喷管的黏性阻力会随着尾喷管入口压强和马赫数的增大而增大,总压损失减小。
本文研究并揭示了经过优化设计的三维截短偏置高超声速尾喷管在非工况情况下工作的性能规律,对装载该类喷管的发动机非设计工况性能预判及飞行器总体设计有指导意义。后续将展开针对不同构型的尾喷管进行非设计工况情况下的对比研究。
致谢:感谢中国航空发动机研究院仿真技术研究中心为本文中运行的算例提供的计算设备的支持。

