基于改进McEvily裂纹扩展模型的新型钛合金疲劳可靠性分析

王 珂，赵春阳，白 旭，屠本阳

(江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003)

0 引 言

钛合金材料广泛地应用于耐压壳结构中，壳体结构在服役期间会承受海水周期性的往复载荷，由此造成的疲劳损伤可能会产生裂纹，成为影响结构安全的重要因素。因此对金属疲劳断裂的分析一直是工程的研究热点。大多情况下，结构疲劳分析采用确定性的方法进行，然而不论是材料特性、载荷本身等都具有不确定性的特征，而这些特征正是影响疲劳寿命的不确定性因素。针对这些疲劳裂纹扩展过程中存在的不确定性，有必要采用可靠性理论[1]对裂纹扩展进行分析。

传统疲劳可靠性方法的缺陷主要是没有考虑到已经存在的裂纹对结构产生的影响，而断裂力学恰好弥补了这一缺点。一些学者提出了可靠性理论与裂纹扩展理论相结合的办法并开展了疲劳裂纹扩展理论工程上的可靠性研究[2-5]，但以往的 Paris疲劳裂纹扩展模型具有很多局限性，它不能包括裂纹扩展的小裂纹阶段。对此，为了解决传统的裂纹扩展模型可靠性分析中存在的局限性，李向阳等[6-8]对新近提出的裂纹扩展模型进行对比，发现McEvily模型能够解释比较多的异常疲劳现象，并提出了针对不同材料的变斜率改进形式，改进后的McEvily模型对疲劳短裂纹和长裂纹均具有良好的疲劳预测能力。随后，王一飞等[9]也将裂纹扩展率分子项的幂指数由固定值改为变量，验证了该模型具备对不同材料的裂纹扩展进行预报的能力。S.Ishihara[10]在钛合金疲劳寿命周期内，进行了一系列高低周循环试验得到了裂纹长度与加载循环次数的函数关系，确定了McEvily模型的本构关系且试验结果与预测结果高度吻合。R.Kumble等基于裂纹张开位移考虑的裂纹扩展模型在应力比R=0载荷情况下，提出了一种修正裂纹扩展表达式以反映裂纹闭合影响下的McEvily关系。李旭东[11]通过对不同温度下6 151-T6合金的研究，获得了一种基于可靠性理论的裂纹扩展速率表达式。罗广恩等[12]基于改进McEvily模型预测深海结构表面裂纹的疲劳寿命，得到了结构的疲劳寿命和表面裂纹扩展的形貌变化。许斐然[13]采用改进McEvily裂纹扩展模型，预测压缩循环载荷下深海结构物的疲劳寿命，并将预测结果与试验结果进行对比，结果表明此模型可为相关循环的压缩载荷下的结构疲劳寿命评估提供参考。康健[14]通过对McEvily公式的深入研究，综合考虑弹塑性行为的影响、裂纹闭合效应，得出McEvily改进公式对疲劳裂纹扩展寿命具有更强的评估能力。这些针对McEvily模型的疲劳裂纹扩展研究也为本文中模型的选取提供了思路。

本文在疲劳分析中引入可靠性理论，将裂纹扩展模型中的不确定参数作为统计变量，结合改进McEvily裂纹扩展模型和疲劳寿命可靠性模型，建立疲劳裂纹扩展可靠性的极限状态方程，利用一次二阶矩法对可靠度指标及参数敏感性进行计算分析，并与传统的Paris裂纹扩展模型可靠度进行对比。

1 基于疲劳裂纹扩展模型的可靠性

1.1 改进McEvily裂纹扩展模型的疲劳可靠性

1.1.1 极限状态方程的建立

疲劳累积损伤模型由于描述的参量不同，因此结构的功能函数有很多种，这就导致在极限状态建立的过程中有了较多的选择。但根据本文的实际情况考虑，应当选择以应力循环数为变量的疲劳寿命模型为结构功能函数，即可表示为：

其中：N为结构在疲劳破坏的临界状态时的循环总数；Nd为设计的应力循环总数。

根据李向阳的改进McEvily模型基础上可以定义裂纹尺寸从a1到扩展到a2时的疲劳损伤累积方程为φ(a1,a2)，它表示的是裂纹扩展疲劳损伤过程。对da/dN=A(M)m进行积分可得：

即可知：

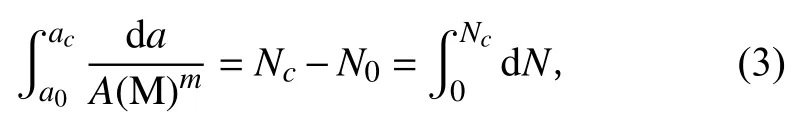
因此可得：

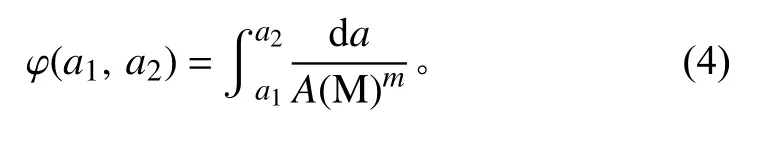
其中，A和m为裂纹扩展过程中的不确定性参数。

φ(a1,a2)是随着裂纹长度递增的函数，因此极限破坏状态可表示为：

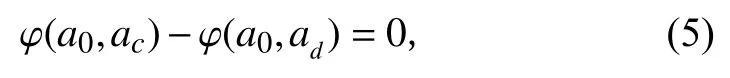
即由此可得结构功能函数：

当疲劳破坏发生时g(x)＜0，g(x)=0为极限状态，即

式中：

其中：R为应力比；a为裂纹长度；k为裂纹闭合水平；re为材料固有缺陷尺寸； σY为材料的屈服强度；Y为应力强度因子修正系数；Kop为裂纹张开水平下的应力强度因子；Keffth为有效应力强度因子范围；Kopmax为裂纹开口状态的最大应力强度因子。

1.1.2 疲劳可靠性分析

由上述内容中提出的基于改进McEvily裂纹扩展模型得到的极限状态方程式（8），当疲劳循环数达到Nd时，表示为：

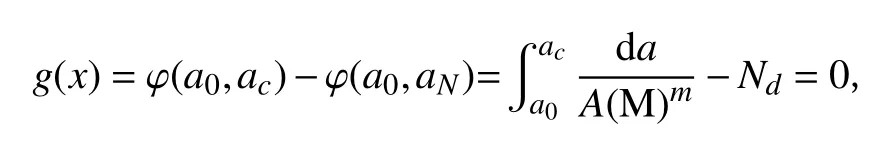
此时的疲劳可靠度可表示为：

根据上面的模型分析可知，所涉及到的主要参量为：不确定材料参数A，m；初始裂纹尺寸a0和临界裂纹尺寸ac；裂纹闭合水平k；材料固有缺陷尺寸re；材料的屈服强度 σY和最大应力 σmax；裂纹的形状参数Y；裂纹开口状态的最大应力强度因子Kopmax；有效应力强度因子范围。其中等参数大多是通过试验拟合或数据分析得到的，并不存在真实的物理意义。因此，这些参数在进行可靠性分析时暂不考虑其统计特性对可靠度指标的影响，通过参考相关文献取值作为常数处理，将值分别设置为0.65，3，3。模型参数的统计特征如表1所示。

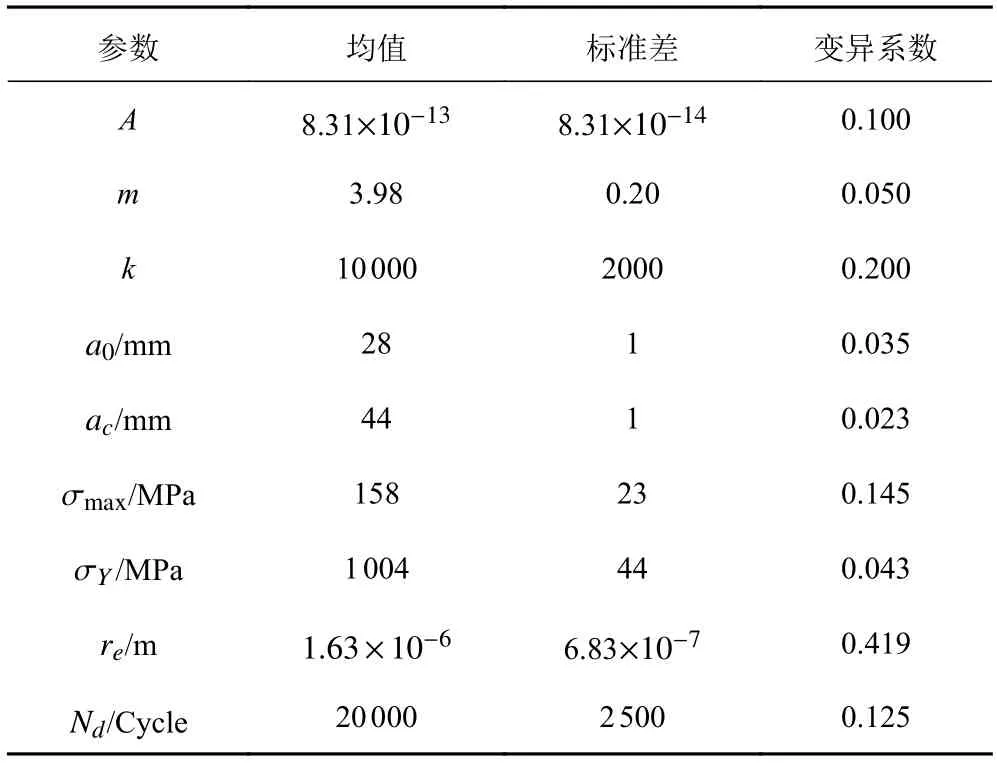
表1 模型参数统计特征Tab.1 Statistical characteristics of random variables

在极限状态模型计算中，默认不确定参数为正态分布。根据一次二阶矩中的中心点法，通过Matlab进行编程计算，可得到裂纹扩展过程中的可靠度指标以及失效概率。本文中基于改进McEvily裂纹扩展模型得到了载人潜水器钛合金材料的可靠度指标 β =4.17，失效概率Pf=1.49×10-5。

1.2 Paris裂纹扩展模型的疲劳可靠性

基于Paris疲劳裂纹扩展模型的极限状态方程及其参数不确定变量的表达式，则当材料循环寿命次数达到Nd时，疲劳可靠度表达式为：

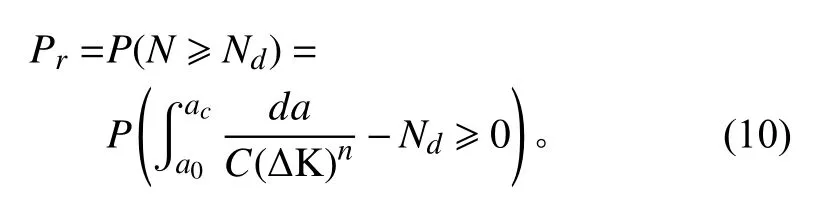
根据上面的极限状态方程所涉及的不确定参数变量主要包括：不确定材料参数C，n；初始裂纹尺寸a0，临界裂纹尺寸ac；疲劳循环次数Nd。通过拟合新型钛合金裂纹扩展速率试验和参考相关文献确定了各不确定参数的均值和变异系数，统计特征值如表2所示。

表2 Paris模型参数统计特征Tab.2 Statistical characteristics of Paris model parameters

基于Paris极限状态计算模型下，不确定参数变量默认为正态分布。采用一次二阶矩的验算点法来进行计算，得到其可靠度为4.08及失效概率为 2.24×10-5。

2 改进 McEvily 裂纹扩展模型的参数灵敏度分析

将模型中各随机变量变异系数取不同数值时对应的可靠度指标和失效概率分别列于图1～图9中。

由以上结果可知，材料参数A、最大应力 σmax、屈服强度 σy、失效寿命Nd、材料固有缺陷re等变量随着变异系数增加其失效概率逐渐增加，呈现出较强的线性关系。其中材料参数m在变异系数达到0.12时，其失效概率曲线速率变化较大。初始裂纹尺寸a0、临界裂纹尺寸ac随着变异系数增加到0.16时，其失效概率呈现大幅增长趋势。

小裂纹扩展过程中的主要影响参数即裂纹闭合水平k，其变异系数从0.16过渡到0.2时，失效速率有进一步增长趋势。其原因可能是，变异系数的改变导致了裂纹扩展速率的增加，进而影响了可靠度的变化。又考虑到，在低周疲劳中的结构70%以上寿命用于小裂纹扩展阶段，因此提出一个包含小裂纹扩展的疲劳可靠性分析模型十分必要。

图1 随机变量A的变异系数对可靠性的影响曲线Fig.1 The influence curve of variation coefficient of random variable A on reliability

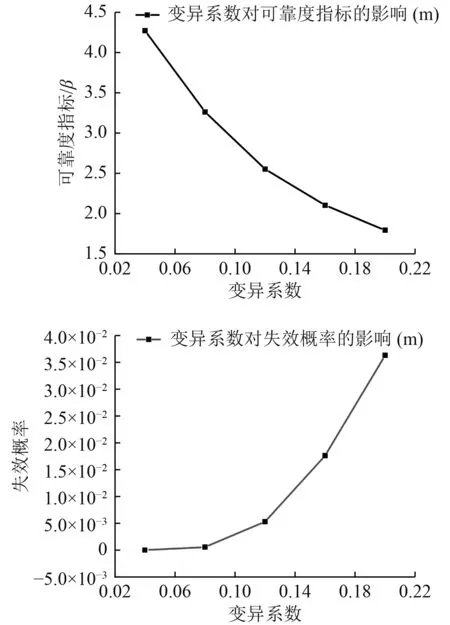
图2 随机变量m的变异系数对可靠性的影响曲线Fig.2 The influence curve of variation coefficient of random variable m on reliability

图3 随机变量k的变异系数对可靠性的影响曲线Fig.3 The influence curve of variation coefficient of random variable k on reliability

图4 随机变量a0的变异系数对可靠性的影响曲线Fig.4 The influence curve of variation coefficient of random variable a0 on reliability

3 结 语

本文基于断裂力学疲劳裂纹扩展理论以及可靠性理论，分别建立了改进McEvily疲劳裂纹扩展公式和Paris疲劳裂纹扩展公式的可靠性计算模型。对提出的计算模型采用了一次二阶矩的验算点法作为可靠性的计算方法。对载人潜水器钛合金材料疲劳裂纹扩展的可靠度指标及参数敏感性进行了计算及分析，得到以下结论：

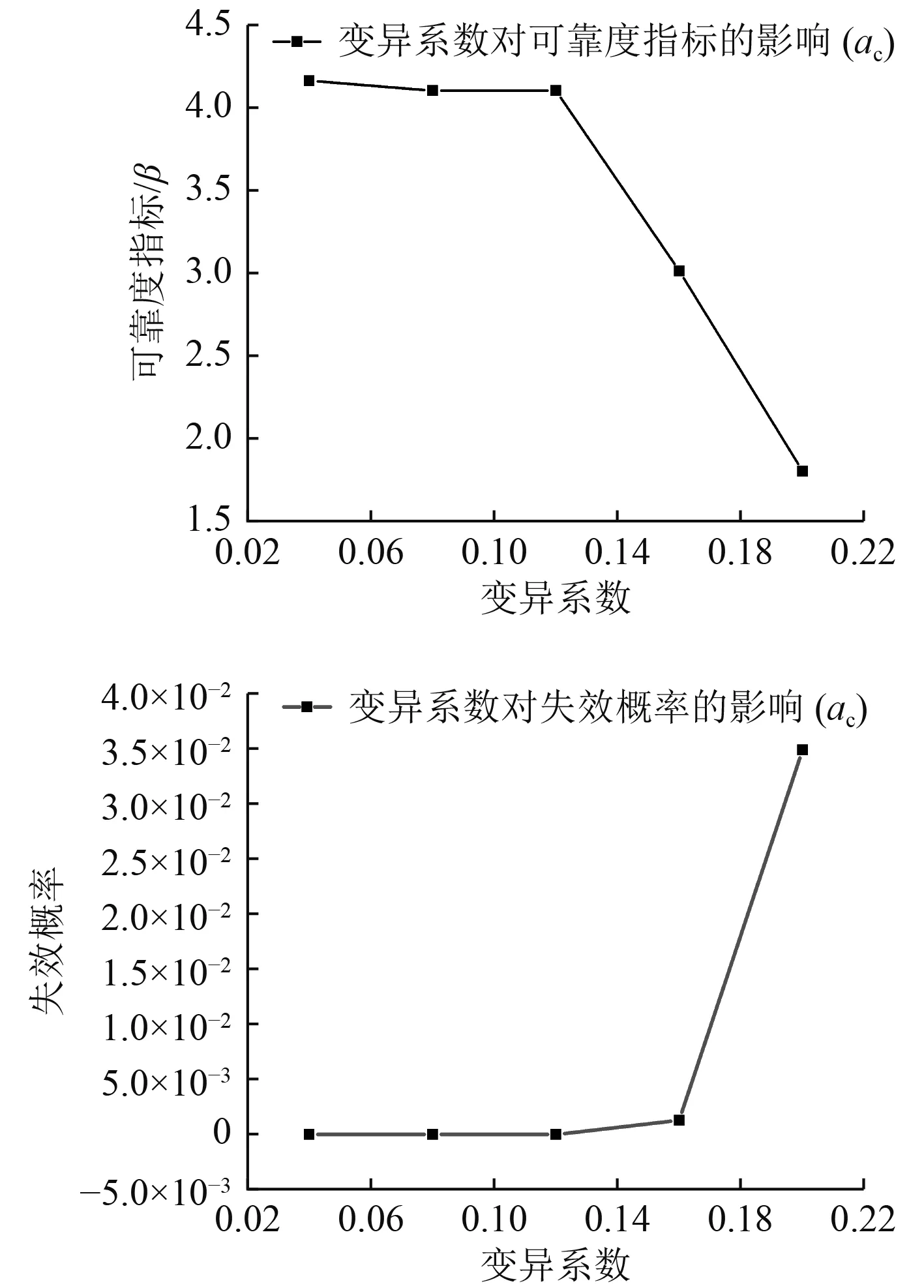
图5 随机变量 a c的变异系数对可靠性的影响曲线Fig.5 The influence curve of variation coefficient of random variable ac on reliability

图6 随机变量 σ max的变异系数对可靠性的影响曲线Fig.6 The influence curve of variation coefficient of random variable σ m ax on reliability

1）基于改进McEvily裂纹扩展可靠性计算模型，经计算得到可靠度指标 β =4.17，失效概率Pf=1.49×10-5。基于Paris裂纹扩展可靠性计算模型，可靠度指标 β =4.08，失效概率Pf=2.24×10-5。Paris模型只考虑了裂纹稳定扩展过程中的可靠性，虽简化模型降低了工作量，但其可靠性计算结果较为保守。

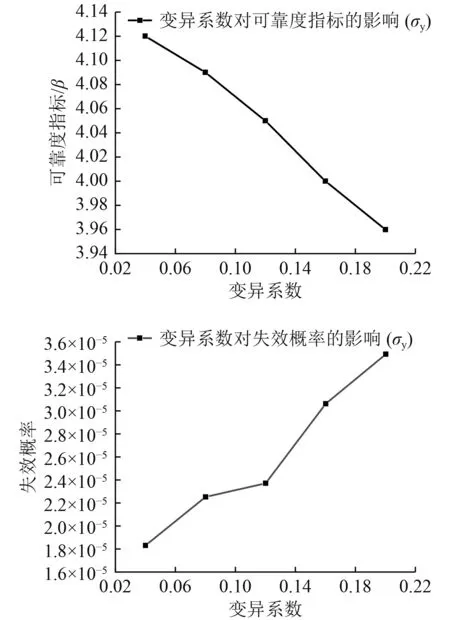
图7 随机变量 σ y的变异系数对可靠性的影响曲线Fig.7 The influence curve of variation coefficient of random variable σ y on reliability

图8 随机变量 r e的变异系数对可靠性的影响曲线Fig.8 The influence curve of variation coefficient of random variable re on reliability

2）基于改进McEvily裂纹扩展模型下的极限状态方程，对模型中随机变量的参数进行了灵敏度分析。不确定材料参数m、初始裂纹尺寸a0和临界裂纹尺寸ac的变异系数分别达到0.12和0.16时，材料的可靠度指标出现了较大程度的下降，失效概率呈现出指数级的上升趋势，存在较大概率的失效风险。其小裂纹扩展阶段中的主要影响参数，裂纹闭合水平k的变异系数对失效概率的总体影响较小但有进一步增长趋势，又考虑到小裂纹扩展阶段占据裂纹扩展过程的主要疲劳寿命，应在设计阶段或可靠性模型建立时给予重视。

图9 随机变量 N d的变异系数对可靠性的影响曲线Fig.9 The influence curve of variation coefficient of random variable N d on reliability