统计思想方法助力社会性议题的项目课程学习

何棋，北京市第一〇一中学数学高级教师，海淀区数学学科带头人，海淀区兼职教研员，主要从事高中数学和国际课程数学教育教学工作。曾受邀到重庆、深圳等多个地区分享信息技术与数学整合教育经验，或上示范课;受邀参加在美国华盛顿召开的全球第17届T3（教师用技术教学）教育会议。多次参与人教社教材研究所国家“十五”“十一五”“十二五”重点课题研究，并被评为课题实验先进个人。个人研究成果多次获海淀区教育创新奖。公开发表论文20余篇，其中2篇被人大复印资料中心转载。出版专著一本，并获第六届北京市教科研优秀成果奖。

[摘   要]在社会性议题的项目课程学习中，学生应用统计学中的分层抽样、方差分析、回归分析、假设检验等思想方法来分析探究“六大洲新型冠状病毒肺炎患者的年龄与死亡率关系”的课题，为解决实际问题提供了更有说服力的证据。同时为学生开展生命教育，增强其抗疫信心，树立民族大义和爱国情怀。

[关键词]社会性议题;统计学;项目课程

一、社会性科学议题

“社会性科学议题”（Socio-scientific Issues，SSI）指由当代科学技术研究开发所引起的一系列与社会伦理道德观念和经济发展紧密相关的社会性问题，目的在于让学生了解科学、科技、社会和环境之间的关联与影响，深入探讨科技研究开发所衍生出的与生活有关的争议性课题，以培养他们解决问题和判断思考的能力，并了解科学的价值、社会人文层面的意义和科学的有限性。

开展和从事 SSI 课程教学实践的学者对课程的意义可以概括为：能够培养学生的非形式推理能力以及正确应用科学知识解决日常生活问题的能力;能够促进学生对相关科学知识的学习和对科学本质的理解;能够指导学生如何对信息进行评估，尤其是当信息较多或信息之间存在冲突时，个体如何对信息进行选择;可以创设各种与学生生活相似的情境，让学生解决其中的伦理道德难题，从而促进学生道德观念和行为的发展。

二、利用统计思想开展社会性议题

统计学是应用数学的一个分支，是收集、处理、分析、解释数据并从数据中得出结论的科学。主要利用概率论建立数学模型，收集所观察系统的数据，进行量化分析、合理描述、直观展示;并且利用具有代表性的样本数据来推断总体特征，做出预测，为相关决策的制定提供依据和参考。

大学先修课程统计学（AP Statistics）是美国大学理事会（The College Board）为高中生准备的大学先修课程中的统计学科目。由于统计学应用广泛，AP统计学的选修人数大幅提升，超过了其它很多的AP科目。课程大纲分为四大部分：第一部分为数据呈现和分析，包括单变量、双变量数据和分类数据;第二部分包括抽样方法和实验设计，学生必须学会通过抽样或实验来进行数据收集，并从中得出结论;第三部分为概率论以及随机变量分布的基础知识;第四部分为统计推断，包括置信区间、假设检验和两类错误等。课程设计是无微积分基础的统计课程，其重点不在于具体数学计算，而是对概念的理解和对统计结果的正确解释，对普通大众正确地、科学地使用统计方法解决问题具有重要帮助。因此，统计思想方法是有助于开展社会性议题的课程学习。

AP统计学全球考试定在每年5月份，结束后距离放暑假大约有1个月的时间，这段时间是学生进行社会性科学议题学习的最佳时机。每年，笔者要求学生在这期间完成一个项目课程学习，大家自愿组队，根据社会热点问题或者自己身边的事情确定问题，应用所学的统计和其他知识来分析和解决问题，最终完成论文，并进行汇报交流。大约4周时间，安排8次课，每周2次，每次2课时，具体计划如下。

第1次课：教师宣布课题项目学习要求，学生自愿组队，讨论选题，确定研究计划和人员分工。

第2次课：分小组展示各组的课题及计划，教师和同学提出建议。

第3次课：根据课题计划开展研究，查阅资料或者网络数据收集，整理数据，初步分析和计算。

第4次课：根据收集的数据，展示应用的统计分析方法和初步计算结果，教师和同学提出修改意见。

第5次课：教师讲解科技论文写作的基本要求、格式和规范，学生根据自己的课题开展情况，完成数据分析，得出结论。

第6次课：学生按照科技论文的格式，书写整理论文。教师单独给小组指导。

第7次课：各小组进行汇报展示，教师和同学进行点评，并且给出评价，提出意见。

第8次课：根据最后的讨论和意见，完成论文。

由于2020年新冠肺炎疫情暴发，学生确定的课题大多与新冠有关，如“英国新型冠状病毒感染比例与地域人口密度相关性分析”“六大洲新型冠状病毒肺炎患者的年龄与死亡率关系的探讨”“新冠病毒感染确诊分布与中国沿海地区1月气温与降水的关系”等。现以“六大洲新型冠状病毒肺炎患者的年龄与死亡率关系”课题为例进行说明（该课题主要由小组成员刘嘉悦、罗泽楠、朱向达完成）。

三、利用统计思想开展社会性议题的具体步骤

2020年5月份，中国的抗疫取得了阶段性的胜利，但西方的抗疫效果并不明显，因此学生想到从死亡率的角度來比较两种抗疫方式的效果，并提出“六大洲的新型冠状病毒肺炎死亡率之间是否存在显著性差异”的问题。

1.研究思路

假设新型冠状病毒对各大洲人群造成的影响相同，那么各大洲的COVID-19死亡率应当是一致的。因此通过方差分析的统计模型对各大洲的COVID-19平均死亡率进行分析，可判断各大洲的COVID-19死亡率是否相同，若p值小于0.05，则差异具有统计学意义。

2.研究过程

采用分层抽样的办法，最终在六大洲中分别随机抽取10、9、12、8、3、5个国家作为样本。其中亚洲国家有伊朗、印度、日本、越南、也门、菲律宾、中国、科成特、乌兹别克斯坦、蒙古;欧洲国家有意大利、英国、比利时、芬兰、法国、匈牙利、德国、瑞典、西班牙;非洲国家有几内亚、贝宁、赞比亚、利比里亚、卢旺达、埃及、利比亚、安哥拉、加蓬、尼日利亚、坦桑尼亚、马拉维;北美洲国家有加拿大、巴拿马、圣卢西亚岛、古巴、美国、巴哈马、阿鲁巴、墨西哥;南美洲国家有巴西、秘鲁、巴拉圭;大洋洲国家有汤加、关岛、巴布亚新几内亚、澳大利亚、新西兰。研究所用数据截止时间为2020年8月6日。

3.研究结果

查找世界卫生组织官方网站公布的疫情数据，计算得出六大洲中欧洲的COVID-19死亡率为9.65%（标准差为0.0446），明显高于其他五大洲。其次是亚洲，COVID-19死亡率为4.84%，但是标准差为0.0863，说明有极端值存在，从数据看也门的死亡率最高达到22.80%，远远超过其他亚洲国家，是造成标准差较大的原因。第三是北美洲，COVID-19死亡率为3.93%（标准差为0.0354）。其中加拿大的死亡率最高，达到7.60%，远远超过其他北美洲国家，也是造成标准差较大的主要原因。南美洲的COVID-19死亡率是2.99%（标准差为0.0182），略高于非洲的COVID-19死亡率2.79%（标准差为0.0192）。大洋洲的COVID-19死亡率最低，仅1.14%（标准差为0.0067）。

对上述死亡率进行方差分析，结果如表1所示。F值为3.87，p值为0.006小于α值（0.05），检验结果具有统计学意义，即六大洲新型冠状病毒肺炎的死亡率存在显著性差异。

进一步追踪数据发现，欧洲新冠肺炎死亡病例中老年人的占比较高，于是提出新的问题，即年龄对死亡率的差異可能存在潜在影响。经过小组讨论和教师指导，大家决定对六大洲人口的平均年龄进行比较，也通过方差分析检验差异是否明显，如果差异明显再对平均年龄和死亡率做出相关分析，最后对欧洲老人死亡率是否超过80%进行统计检验，来说明问题。

从worldometers网站（2020年）收集到六大洲样本中各国家人口的平均年龄数据，经过统计分析得出：六大洲中欧洲人口的平均年龄为43.30岁（标准差为2.08），明显高于其他五大洲。其次是北美洲，人口的平均年龄为36.00岁（标准差为5.30）。第三是亚洲，人口的平均年龄为31.80岁，但是标准差为7.87，说明有极端值存在。从数据看，日本人口的平均年龄最高，达48.40岁，远远超过其他亚洲国家，是造成标准差大的原因。大洋洲人口的平均年龄是30.40岁（标准差为7.80）。其中汤加和巴布亚新几内亚人口的平均年龄最低，为22.40岁，远远低于其他三个大洋洲国家，也是造成标准差较大的主要原因。南美洲人口的平均年龄30.30岁（标准差为3.66），略低于大洋洲人口的平均年龄。非洲人口的平均年龄最低，仅20.10岁（标准差为3.55）。

对平均年龄进行方差分析，结果如表2所示。F值为20.55，p值为0.00小于α值（0.05），检验结果具有统计学意义，即六大洲人口的平均年龄存在显著性差异。

将平均年龄视为解释变量x，死亡率视为结果变量y，进行线性回归分析，模型假定如下yi=？茁0 + ？茁1xi + εi，εi～N（0，σ2）且相互独立。

提出假设：

H0：六大洲COVID-19死亡率与人口平均年龄的线性回归线斜率为0，即β1 =0。

Hα：六大洲COVID-19死亡率与人口平均年龄的线性回归线斜率大于0，即β1>0。

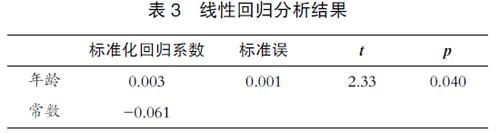
采用T-inspire图形计算器做出散点图、残差图、残差正态概率图进行条件检验，结果满足进行回归分析的条件。回归分析结果如表3所示，t值为2.33，p值为0.04，小于α值（0.05），检验结果具有统计学意义，拒绝原假设，即六大洲COVID-19死亡率与人口平均年龄的线性回归线斜率大于0，说明两者之间存在正向线性关系。

得到回归方程是= 0.003303x-0.0611，斜率是0.003，表明每当人口平均年龄增加一岁，死亡率平均增加0.3%。y轴截距是-0.061，表明当人口平均年龄为0时，死亡率为负6.1%，不具有现实意义。判别系数r2为0.5761，表明人口平均年龄引起的死亡率变化大约占57.61%即线性模型可以解释57.61%的死亡率的变化。

由于未找到其他国家的死亡人数的年龄分布，这只分析欧洲（COVID-19死亡率最高的大洲）新型冠状病毒肺炎死亡人员中70岁以上老年人的比例，检验该比例是否超过80%。在论文《COVID-19-related mortality by age groups in Europe： A meta-analysis》中查找了欧洲样本国家的新型冠状病毒肺炎死亡人员的年龄分布。

提出假设：

H0：欧洲新型冠状病毒肺炎死亡人员中70岁以上老年人的占比等于0.8，即P0=0.8。

Hα：欧洲新型冠状病毒肺炎死亡人员中70岁以上老年人的占比大于0.8，即P0>0.8。

欧洲样本国家因COVID-19的总死亡老年人人数（70岁以上）为24680，总死亡人数为29030，70岁以上老年人的占比■=24680/29030=0.85，检验统计量Z为21.36，p显著小于0.05，结果具有统计学意义，即欧洲新型冠状病毒肺炎死亡人员中70岁以上老年人的占比大于0.8。由此说明，保护老年人可有效降低新冠肺炎的死亡率。

四、其他问题分析

在问题解决的过程中，学生还通过查询资料对其他问题进行了分析。如早期测试人数是影响新型冠状病毒肺炎死亡率的潜在因素。与美国和西班牙没有及时采取措施和检测的国家相比，较早开始检测的德国的死亡率更低。快速且有效地应对疫情能够直接影响死亡率。比如，新加坡、中国和加拿大都面对过2003年的非典传染病。相关经验让这些国家可以对类似疫情采取快速、有效的措施，从而减少病毒的传播，降低死亡率。

此外，医疗系统的容量大小在很大程度上决定了疫情死亡率的高低。以意大利为例，平日里的患者数量不大，因此医疗设施在正常情况下是能够满足需求的。但是在疫情暴发后，病患人数大量增多，医院超负荷运转。设施短缺，医生人手不够，也就导致了许多患者得不到及时的治疗而死亡。这是意大利等欧洲国家疫情死亡率高的原因之一。而中国采取了强有力的措施，迅速地扩充医疗系统容量，比如在雷神山和火神山的医院项目，这帮助中国有效地控制了死亡率和疫情。

主动还是被动控制疫情也是影响死亡率的因素。主动控制疫情的国家会在疫情尚未形成大范围传播的态势前就采取强有力的措施去管控。而被动控制疫情的国家则会等到疫情发展到一定严重程度的时候才会采取相应的措施。中国是典型主动防控的国家。在2020年6月11日、12日，北京第二次疫情暴发时，北京西城、丰台共新增3例新冠肺炎确诊病例。但政府在发现新增病例后的短时间内，便完成了溯源、隔离、消杀等工作，有效抑制了疫情大范围的传播。而英国等国家则采取被动控制疫情。英国采取了对疫情的五级风险评级，根据疫情的严重程度再采取措施，属于被动防疫。

综上，统计的思维和方法可以帮助学生在解决实际问题时提供更有说服力的证据，同时也让学生进一步体验了统计思想方法的实际应用。此外，通过课程项目的学习，学生们也深深感受到了大家齐心协力共同抗疫的重要性，并且能够深刻理解国家的防疫政策，自觉用行动来支持，做好个人相关防疫事务。

参考文献（编者略）

（责任编辑   姚力宁）