反常涡旋光束在各向异性大气湍流中的漂移

杨盛凯，王晓艳，赵 亮，徐勇根

(西华大学 理学院，成都 610039)

引 言

近年来，激光技术的不断发展，使得其在众多领域，如信息通讯、生物、材料、化学、国防等方面有着广泛的应用。研究中，一种具有轨道角动量(orbital angular momentum，OAM)的涡旋光束引起了学者们的注意[1-3]。不同于普通的高斯光束，部分相干反常涡旋光束(partially coherent anomalous vortex beam，PCAVB)的OAM可以提供相当数量的复用信道用于信息传输[4]。携带OAM的光子有着更高的安全性、保密性和隐蔽性[5]，故而涡旋光束在光通讯领域中具有较高的研究意义。而光束在大气传输中，由于受到大气湍流的影响，光束会出现一系列的湍流效应，例如光束扩展、漂移以及光强闪烁等现象[6-8]。因此，为提高涡旋光束的传输性能，研究其在大气湍流中的传输特性具有重要的现实意义，尤其在大气激光雷达探测与成像等方面有重大研究价值。

YANG等人[9]研究发现的一种新型的反常涡旋光束(anomalous vortex beams,AVB)引起研究人员的广泛关注。该光束(光强)在源平面(z=0)处的分布呈圆环形状，在自由空间远场又会演变成复宗量拉盖尔-高斯光束。YUAN等人[10]研究了反常涡旋光束在大气湍流中的斜程传输特性。XU等人[11]研究了反常涡旋光束在特定光学系统中的传输特性。而以上工作局限于部分相干光束在各向同性大气湍流中的传输。大气湍流存在各向异性得到了实验验证[12]，非Kolmogorov湍流功率谱模型不再适用描述各向异性大气湍流,因此，激光在各向异性湍流的传输特性具有较高的研究价值。PCAVB在各向异性大气湍流中的漂移特性还鲜有研究。本文中采用交叉谱密度矩和扩展的惠更斯-菲涅耳原理相结合的方法得出光束漂移的解析式，并对其进行数值模拟，主要研究光束的相干长度、拓扑荷与湍流各向异性因子对光束漂移的影响。

1 理论模型

基于涡旋光束的模型，PCAVB在源平面上的电场分布可以表示为[13]：

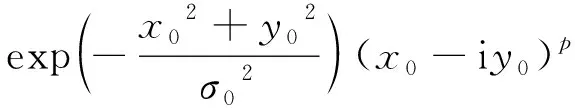
(1)

式中,ε0为常数，σ0为高斯光束的束宽，l表示光束阶数，x0和y0表示入射面上任意位置坐标,p表示光场拓扑荷数。当p在一个周期内，光束相位从0变化到2πp，拓扑荷数在传输过程中不会发生改变，且一般取整数值，理论上该值的取值没有上限[14-15]。涡旋光束在源平面(z=0)上的2阶统计特性可以用一个2×2交叉谱密度函数矩(cross spectral density matrix，CSDM)表示[16-17]：

W(r01,r02;0)=

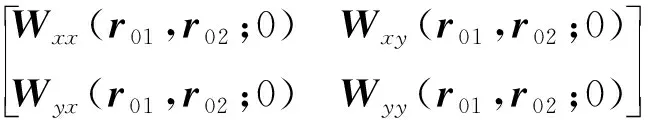
(2)

式中,r01和r02是源平面(z=0)上的任意两个位置矢量，Wab(r01,r02;0)=〈εa*(r01;0)εb(r02;0)〉m，(a,b=x,y),εx和εy表示在x和y方向上的电场分量，*为复共轭，〈·〉m表示系综平均。为了简化运算，可以假设PCAVB的场强εx和εy不相关，即Wxy(r01,r02;0)=Wyx(r01,r02;0)=0。

这里对角元素Wxx(r01,r02;0),Wyy(r01,r02;0)可以表示为[13]：

(a=x,y)

(3)

式中，φ01和φ02表示方位坐标;δxx和δyy分别表示x和y方向上的相干长度，相干长度越大，光束相干性越好;波数k=2π/λ，λ为波长。研究表明，部分相干光在湍流中的传输性能优于完全相干光[18]，部分相干光的相干长度在一定范围内减小时，能够有效减小光束相位波前发生变化，进而使光束漂移下降。相干长度太大，激光的相干性越优异，使得激光在大气湍流中的传输不易发散，但容易出现光斑，使得传输质量降低；相干长度太小，光束相干性差，会使激光在大气湍流传输中极易发散，有效传输距离大大降低。

利用扩展的惠更斯-菲涅耳原理的近轴形式，PCAVB经过大气湍流后在接收平面上的CSDM可以表示为[19-22]：

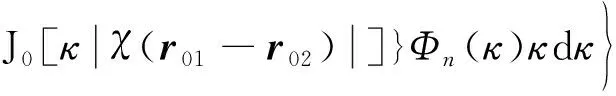
(4)

式中，J0(·)是零阶贝塞尔函数，r1和r2是接收面上的两个位置矢量，Φn(κ)为湍流的空间功率谱函数，z为传输总长度，κ是空间波数的大小，χ=h′/zcosγ，h′为传输高度变量，γ为天顶角。令r1=r2=r，将(3)式代入(4)式可得PCAVB在湍流中传输时接收面交叉谱密度函数的解析式[13]：

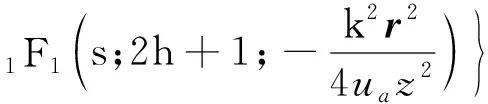
(5)

式中,Γ(·)是伽马函数，1F1(·)是库默尔函数。h=0时，δh,0=1；h≠0时，δh,0=0。

s=l+p+q+2h+1

(6)

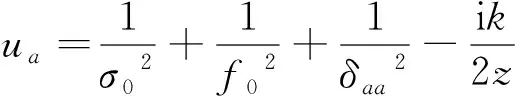
(7)

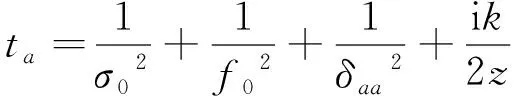
(8)

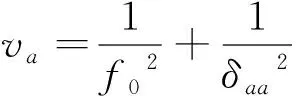
(9)

式中，a=x,y。球面波在接收面上的空间相干长度表示为[23]：

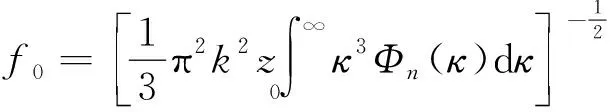
(10)

PCAVB的平均光强可以表示为[13]:

I(r,z)=Wxx(r;z)+Wyy(r;z)

(11)

将(5)式代入(11)式，可以得到[16-17,24]：

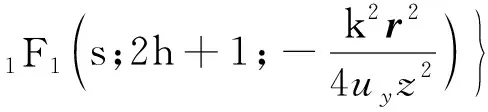
(12)

初始平面上PCAVB的偏振度可表示为[13]：

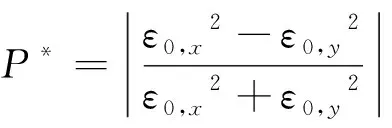
(13)

在各向异性湍流中，PCAVB的均方根空间宽度可定义为[25]：

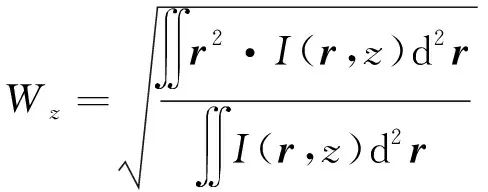
(14)

将(12)式代入(14)式可得[13]：

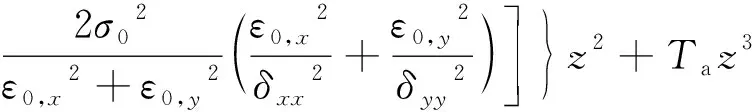
(15)

式中，Ta为各向异性大气湍流量[20]：

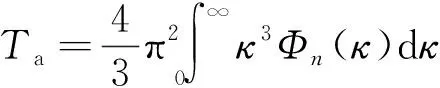
(16)

引入各向异性功率谱模拟大气湍流，在各向异性湍流中，功率谱的形式由下式给出[12,26]：

(0≤κ<∞，3<α<4)

(17)

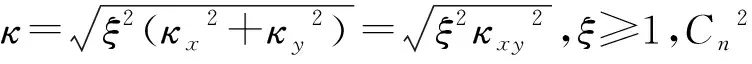
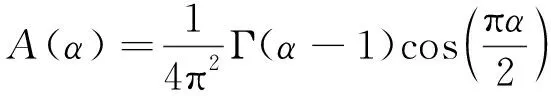
(18)

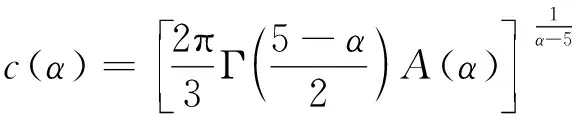
(19)

将(16)式～(19)式整理合并，得到：

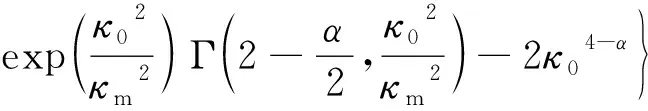
(20)

将(15)式、(20)式整合：

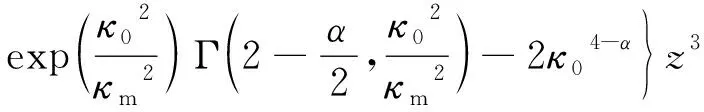
(21)

用几何光学近似与Rytov近似解，可以得到湍流条件下光束漂移的二阶矩模型[27]：

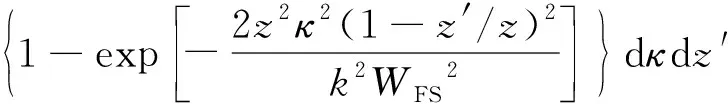
(22)

式中，z′代表在传输总长度z的范围内，源平面到截取点之间的距离，WFS为光束在自由空间中的束宽扩展，利用光束在湍流中传输的漂移模型公式可得[27]：

[2κ02(κm2Wz2)+1+(α-2)κm2]×

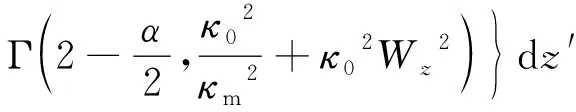
(23)

式中，Γ(·,·)是不完全伽马函数，光束的均方根漂移与相对漂移的表达式为[28]：

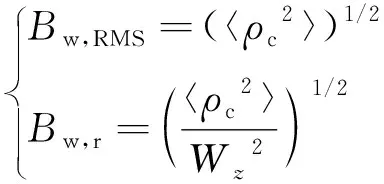
(24)

光束的均方根漂移表达出光束偏离中心的真实距离，相对漂移能够直观反映出光束漂移与光束扩展之间的关系。最新的实验研究表明[29]，用本文中的方法推导出的光束漂移理论模型适用于任意部分相干光束在大气湍流中传输的漂移，且理论结果与实验数据吻合。本文中采用的部分相干光束为反常涡旋光束也适用此模型。

2 数值模拟与分析

图1描述折射率结构常数Cn2、各向异性因子ξ、光场拓扑电荷数p,以及相干长度δxx和δyy对均方根漂移Bw,RMS和相对漂移Bw,r的影响。通过图1a、图1b可以看出，随折射率结构常数Cn2的增加，湍流强度变大，对反常涡旋光束在湍流中的漂移影响越大，导致光束均方根漂移Bw,RMS和相对漂移Bw,r增大。这是因为湍流强度的增加，直接导致光束传输时的相位波前发生较大变化，进而使得折射率发生较大改变，使光束漂移更加剧烈。传输距离15km时，Cn2=10-13m3-α的大气湍流对光束漂移影响最大，Bw,RMS接近0.25m，Bw,r接近0.05。图1c、图1d中描述各向异性因子ξ的影响情况。可以看出，当ξ=1时，对光束漂移的影响最大，说明光束受到各向异性湍流的影响比各向同性湍流要小，这是因为ξ影响着湍流强度的分布，各向异性因子ξ越大，强度分布越不均匀，导致湍流对光束漂移的影响降低，光束均方根漂移Bw,RMS和相对漂移Bw,r减小。图1e、图1f表明，光场拓扑电荷数p增大，会使光束抵抗湍流对其漂移特性的影响的能力越强，Bw,RMS和Bw,r下降。传输距离为15km、光场拓扑电荷数p从0增加到10时，Bw,RMS在0.09m～0.1m范围内逐渐减小，Bw,r在0.008～0.01范围内逐渐减小。由图1g、图1h可以看出,传输距离15km时，相比其它两组相干长度，δxx=20mm，δyy=30mm的光束受到各向异性湍流影响最大，Bw,RMS略超过0.08m，Bw,r略超过0.06。而图1b、图1d、图1f、图1h还说明，PCAVB在各向异性湍流传输时，前5km相对漂移Bw,r上升速率最快，传输至5km后，相对漂移Bw,r逐渐趋于稳定状态，相较5km内的漂移程度，没有太大的幅度变化。说明光束经过长程传输后，PCAVB在各向异性湍流传输时的相对漂移逐渐趋于稳定。

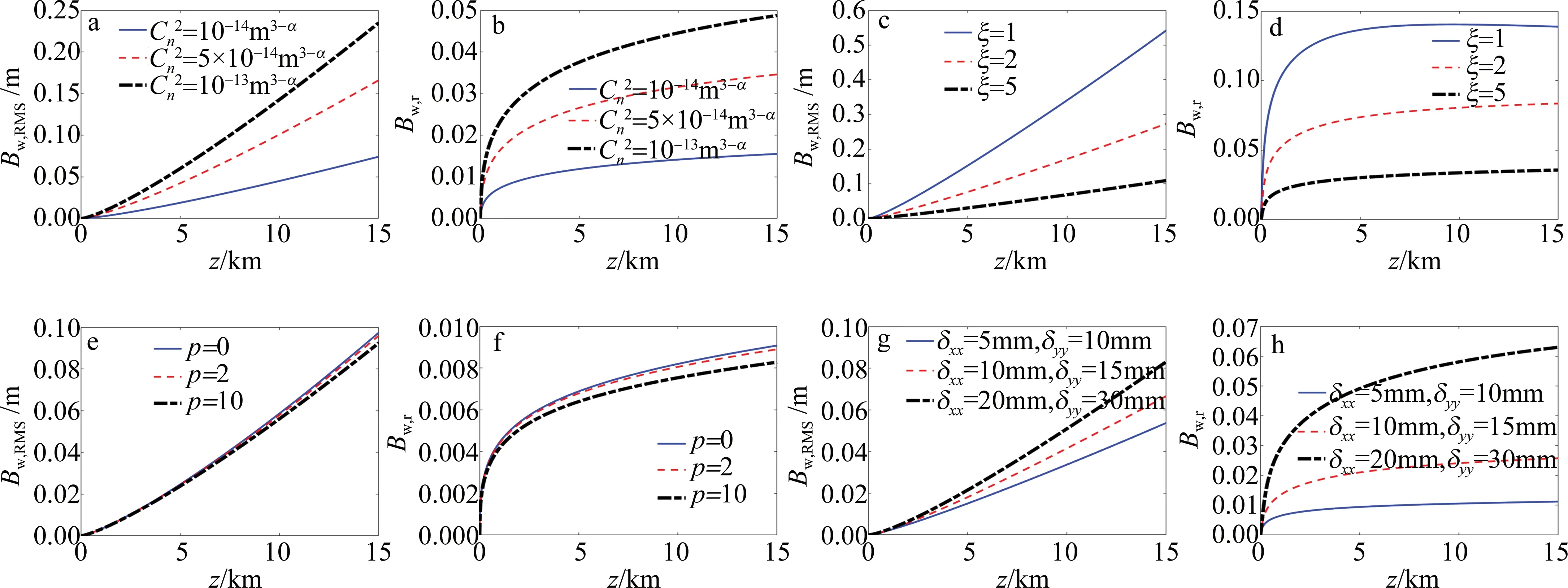
Fig.1 In the anisotropic turbulence, the root mean square wander Bw,RMS and relative wander Bw,r of PCAVB vary with each parameter

图2反映出广义指数参量α与光束漂移之间的关系。通过图2a、图2b看出，当α在3～3.1与3.6～4之间变化时，拓扑电荷数p的增加，对光束均方根漂移Bw,RMS和相对漂移Bw,r的影响不大，而当α在3.1～3.6之间取值时，随拓扑电荷数p的增加，光束均方根漂移Bw,RMS和相对漂移Bw,r减弱。图2c、图2d中，各向异性因子ξ=5时，相比ξ=1与ξ=3，随着α的增加,Bw,RMS与Bw,r更快达到饱和状态，且光束漂移最小，Bw,RMS不超过0.1m，Bw,r稍稍高于0.02。由图2e、图2f可以看出，相干长度越大，α也要取越大的值，才能使光束漂移达到饱和，其中相干长度δxx=5mm，δyy=10mm时，光束漂移最小，Bw,RMS接近0.17m，Bw,r稍高于0.02。由图2a～图2f可以看出,广义指数参量α在3.0～3.3之间变化时，Bw,RMS和Bw,r迅速增大，变化最为明显。当α在3.3～4.0之间变化时，Bw,RMS与Bw,r随α的增大逐渐上升，但变化速率没有α在3.0～3.3变化时迅速，并很快趋于饱和。说明随着α的增大，对光束漂移的影响趋近饱和，不显著影响PCAVB在各向异性反常涡旋大气湍流中的漂移现象。

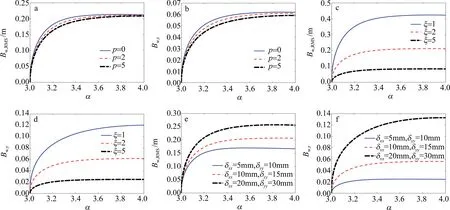
Fig.2 In the anisotropic turbulence, the root mean square wander Bw,RMS and relative wander Bw,r of PCAVB vary with the generalized exponential parameters α

Fig.3 In the anisotropic turbulence, the root mean square wander Bw,RMS and relative wander Bw,r of PCAVB vary with the transmission distance z, anisotropic factor ξ, coherence length δxx,δyy

图3a、图3b直观反映出随传输距离的增加，Bw,RMS持续增加，而Bw,r的增加量逐渐减少并趋于饱和。这是因为随传输距离的增加，光束束宽扩展也随之增加，并与Bw,RMS的比值逐渐趋于某一值的缘故。同时可以看出，各向异性因子ξ越大，对光束漂移的抑制作用越明显，光束在ξ=6的大气湍流中传输至15km时，光束Bw,RMS与Bw,r同ξ=1的大气湍流中相比，光束漂移量减少了数倍，大大减少了光束漂移。图3c、图3d中描绘出了相干长度与光束漂移之间的关系，相干长度δxx与δyy越大，光束的相干性越好，Bw,RMS和Bw,r越大。在光束的选取上，应选部分相干光束以降低湍流对光束漂移的影响。

3 结 论

通过采用交叉谱密度函数与扩展惠更斯-菲涅耳原理相结合的方法，几何光学近似与Rytov近似解得到了PCAVB在各向异性非Kolmogorov湍流中传输的光束漂移解析式，数值模拟分析了湍流与光束参量对Bw,RMS和Bw,r的影响。模拟结果表明：各向异性因子ξ的增长，会使Bw,RMS和Bw,r明显降低，与ξ=1时的Bw,RMS和Bw,r作对比，ξ=2时减弱了2/5左右，传输15km时,Bw,RMS仅不到0.3m，Bw,r≈0.08。可以看出,各向异性因子在光束于大气湍流传输中，对Bw,RMS与Bw,r有着不可忽视的影响。当传输至15km时，广义指数参量α在3～3.3增长，对Bw,RMS和Bw,r的影响最为明显，两者迅速增加；α在3.3～4之间变化时，随着α的增加，Bw,RMS和Bw,r变化不大，且均呈现出增长饱和的趋势，可以看出，α对部分相干反常涡旋光束的漂移影响，集中于α取值3～3.3之间。拓扑荷数p对部分相干反常涡旋光束在各向异性大气湍流中的漂移有一定抑制作用，拓扑荷数越大，Bw,RMS和Bw,r越小。部分相干反常涡旋光束的相干长度δxx和δyy极为明显地影响着光束漂移，随着δxx和δyy增加数值越大，Bw,RMS与Bw,r的变化越大。部分相干反常涡旋光束的相干性越好，反而会增大其在各向异性湍流中的漂移，当δxx，δyy均取值5mm时，光束漂移最小。

综上所述，在各向异性因子ξ越大、广义指数参量α越小的各向异性非Kolmogorov的大气湍流中，拓扑荷数p越大、相干长度δxx与δyy越小的PCAVB漂移现象被抑制得越好。为了减小大气湍流引起的光束漂移，应选取拓扑荷较大、相干长度越小的PCAVB作为传输光束。该结论可以应用在实际雷达探测中，为其选取光束提供一定的理论指导与参考价值。