键合Nd∶YAG/Cr4+∶YAG被动调Q微片激光器的优化设计

刘瑞科，王超臣，牛昌东，金 舵，白振旭,2，王雨雷,2，吕志伟,2*

(1.河北工业大学 先进激光技术研究中心，天津 300401；2.河北工业大学 电子信息工程学院 天津市电子材料与器件重点实验室，天津 300401)

引 言

半导体可饱和吸收镜(semiconductor saturable absorption mirror,SESAM)和可饱和吸收晶体(如Cr4+∶YAG,MoS2等)是目前实现被动调Q的主要调Q器件[7-9]。BHANDARI和TAIRA使用复合Nd∶YAG/Cr4+∶YAG微片激光器实现了峰值功率大于6MW、脉冲能量为1.7mJ、脉冲宽度为265ps的激光输出[10]。YIN等人采用SESAM实现了脉冲宽度为219ps的调Q激光输出[11]。Cr4+∶YAG具有成本低、损伤阈值高、使用寿命长等优点，目前已广泛应用于Nd∶YAG晶体、Yb∶YAG晶体等作为工作物质的被动调Q激光器中[12-14]。Nd∶YAG具有较大的受激发射截面、阈值反转粒子数低等优点。复合的Nd∶YAG/Cr4+∶YAG微片激光器通过使用晶体的长度作为谐振腔的腔长，缩短激光器的谐振腔长度，当腔长小到使腔纵模间隔大于或等于Nd∶YAG的荧光线宽时，有助于实现单纵模输出；此外，复合的Nd∶YAG/Cr4+∶YAG还有助于降低热效应。除了采用复合晶体外，人们通过Cr与Nd或Yb互掺的晶体也实现了自调Q的激光输出，但是自调Q激光器获得的峰值功率和脉冲能量一般小于复合晶体激光器，且热效应较为严重[15-18]。因此，复合Nd∶YAG/Cr4+∶YAG微片激光器作为一种具有较强可行性的技术方案，近几年得到了国内外学者的广泛报道[19-21]。

根据被动调Q理论公式推导出被动调Q微片激光器输出特性的相关表达式。为了使理论结果更接近于实际情况，在对被动调Q微片激光器的重要输出参量进行数值仿真时，将自发辐射和抽运速率等因素对激光器性能的影响考虑在内。分析了微片激光器结构中若干因素对其输出特性的影响，为理论指导实验奠定了基础。

1 被动调Q微片激光器理论分析

将粒子的自发辐射与抽运速率考虑在内的被动调Q速率理论公式如下[22]：

2σeNels-ln(1/R)-L]

(1)

dN/dt=-γcφN-N/τ+wp

(2)

dNg/dt=-σgcφNg+(Ns-Ng)/τs

(3)

Ng+Ne=Ns

表2还列示了主要变量的描述性统计。首先，企业获得创新科技财政补助项目数量(Subsidy_item)从供给侧改革前的平均8.691个提升到了供给侧改革后的12.58，说明创新科技补助的来源正在变得更加多元化。但是，来源于地方创新补助项目的比重(Subsidy_local)从改革前的39.7%下降到了25.2%，初步表明供给侧创新科技补助改革后，地方政府对于创新补助开始收紧，清理相关政策。

(4)

式中，φ是光子数密度;t为时间;σ为吸收截面；N是Nd∶YAG反转粒子数密度；l是Nd∶YAG的长度；ls是Cr4+∶YAG的长度；tr是光子在激光器谐振腔中的往返时间，tr=2lc/c，lc是激光器谐振腔的长度，c是真空中的光速；Ng和Ne分别Cr4+∶YAG的基态以及激发态的粒子数密度；Ns是Cr4+∶YAG总的粒子数密度；σg和σe分别是Cr4+∶YAG的基态吸收截面、激发态吸收截面；R是反射率;L是激光器谐振腔的耗散性损耗；wp是抽运速率,它与连续波抽运功率成正比关系，wp=Pin[1-exp(-αl)]/(hνpApl)，Pin是输入抽运功率，hνp是抽运光子能量，Ap是抽运光束截面面积，α是Nd∶YAG的吸收系数；τ是Nd∶YAG的激光上能级的荧光寿命；τs是Cr4+∶YAG的恢复时间；γ是反转因子。

由于脉冲建立的时间非常短，所以在脉冲期间可以忽略抽运速率，增益介质上能级寿命的影响，因此(2)式可写为：

dN/dt=-γcφN

(5)

当激光器谐振腔内光子数密度接近于零时，谐振腔中的光强非常弱，不足以将可饱和吸收体基态的粒子数抽运到激发态，此时它的粒子数将全部处于基态，即Ns=Ng。因此由(1)式可得到激光器初始反转粒子密度为：

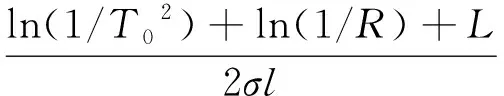
(6)

式中,T0=exp(-σgnsls)为可饱和吸收体的初始透过率。

当激光器谐振腔中的光子数密度达到最大值时，反转粒子数密度处于阈值，此时处于可饱和吸收体基态的大部分粒子将被抽运到激发态，剩余在基态的粒子数几乎可以忽略，所以，Ne≈Ns，并且(1)式的右边dφ/dt=0。所以可以由(1)式得到激光器阈值反转粒子数密度为:

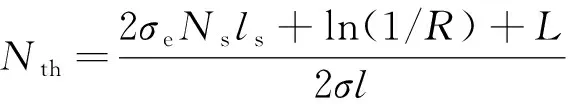
(7)

根据(7)式，可以将(1)式改写为：

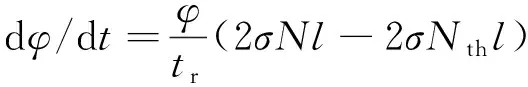
(8)

从(8)式可得到：

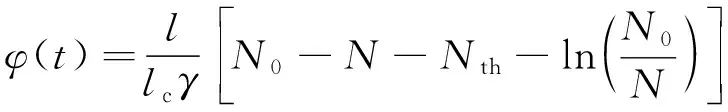
(9)

当初始反转粒子数密度N0降低到阈值时，光子数密度将上升到最大值，所以可得到峰值光子数密度为：

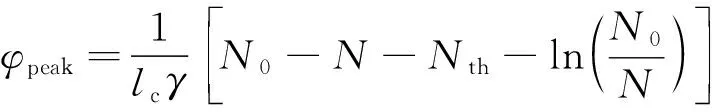
(10)

当脉冲结束时，激光谐振腔内的光子数密度将降低到最低值(近似为零)，而工作物质中的反转粒子数密度不会降低至零，仍然有部分粒子处于反转状态，设剩余反转粒子数密度为Nf，所以由(9)式可得到：

N0-Nf-Nth-ln(N0/Nf)=0

(11)

在被动调Q方式下，激光器的输出参量(单脉冲能量E，峰值功率P，脉冲宽度tp)表达式可写为[23]：

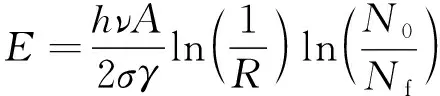
(12)

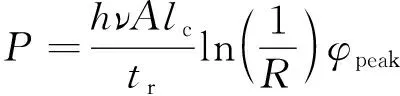
(13)

tp=E/P

(14)

式中，hν是光子能量，A是截面面积。通过(6)式、(7)式、(11)式可求出N0，Nth，Nf的数值，将其代入(11)式～(14)式即可求出单脉冲能量E、峰值功率P、脉冲宽度tp的值；平均输出功率为Pav=Ef，其中,f为激光脉冲重复频率。

2 数值仿真

数值仿真所基于的键合Nd∶YAG/Cr4+∶YAG微片激光器结构如图1所示。将Nd∶YAG晶体与Cr4+∶YAG晶体键合在一起，Nd∶YAG的一侧镀波长为808nm的高透膜(antireflection,AR)、1064nm的高反膜(high neflection,HR)，Cr4+∶YAG的一侧镀波长为1064nm部分反射膜作为输出耦合镜(output coupler,OC)，因此晶体总长度即为谐振腔的长度。对考虑了抽运速率和自发辐射影响的速率方程使用龙格-库塔法对速率方程组求数值解。用于仿真的Nd∶YAG与Cr4+∶YAG参量如表1所示。

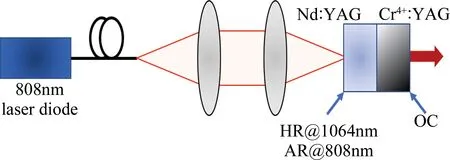
Fig.1 Schematic diagram of Nd∶YAG/Cr4+∶YAG microchip laser

Table 1 Parameters for the simulation

输出耦合镜的反射率和可饱和吸收体的初始透过率对激光器的输出性能有一定的影响。当抽运光斑半径为100μm，Nd∶YAG中激光基模的半径为100μm，抽运功率为4.5W时，图2中给出了激光器的峰值功率、脉冲能量、脉冲宽度、重复频率、平均输出功率在不同的Cr4+∶YAG的初始透过率下随着输出耦合镜的反射率变化曲线。

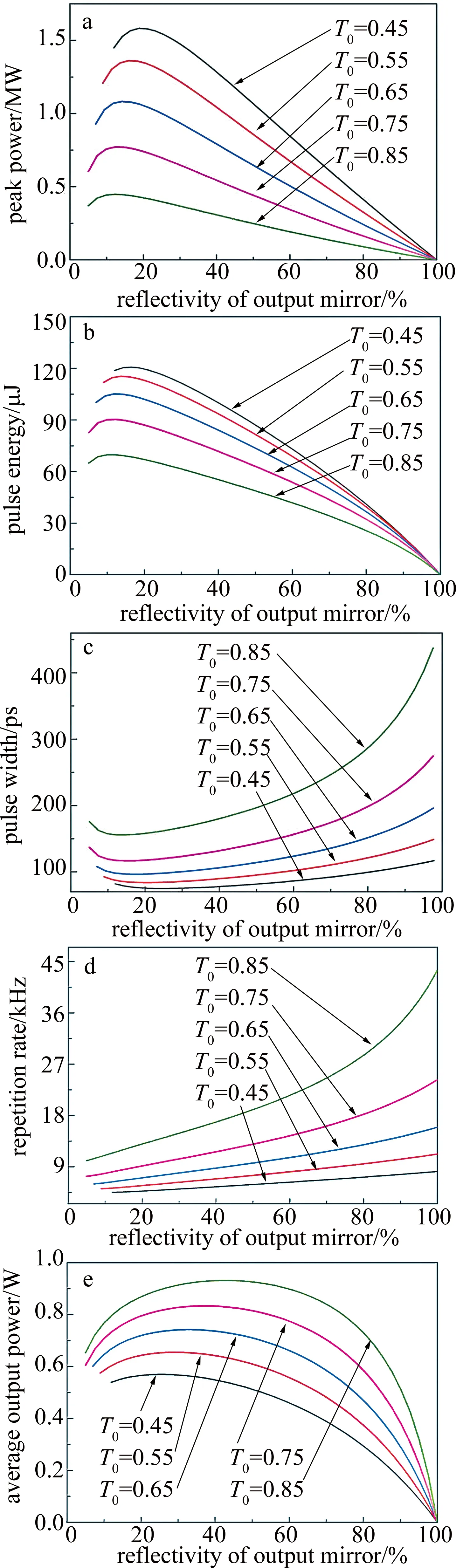
Fig.2 Relationship between the reflectivity of output mirror and other parameters at different initial transmitttance of Cr4+∶YAG

由图2可见， Cr4+∶YAG的初始透过率T0一定，当增大输出镜反射率时，由图2a、图2b可见,输出激光的峰值功率和脉冲能量将随之先增大后减小，所以存在最佳输出镜反射率使峰值功率和脉冲能量存在最大值，并且在不同Cr4+∶YAG的初始透过率T0下对应不同的最佳输出镜反射率；由图2c、图2d可见,脉冲宽度和重复频率将随之增大，这是由于增加输出镜反射率使激光器的损耗降低，谐振腔中的光强变强，从而导致Cr4+∶YAG连续两次被“漂白”的时间间隔缩短，激光脉冲输出的时间间隔变小；此外，由于输出镜反射率增加，使光子在谐振腔中的往返次数增加，从而导致激光器脉冲宽度增加；由图2e可见,平均输出功率则呈先增加后减小，所以存在最佳输出镜反射率使平均输出功率具有最大值；由图2e可见，Cr4+∶YAG的初始透过率T0为0.45，0.55，0.65，0.75，0.85时，所对应的输出镜的最佳反射率为23%，30%，35%，40%，55%。而当输出镜反射率一定时，增大Cr4+∶YAG的初始透过率，输出激光的峰值功率和脉冲能量将随之减小，这是由于Cr4+∶YAG初始透过率T0的增加导致激光器的储能降低；而同时这将导致其它3个输出参量(脉冲宽度、重复频率、平均输出功率)增大。因此为了增大峰值功率以及脉冲能量、缩小脉宽，应当适当的减小输出镜反射率，但同时考虑到其对脉冲重复频率、平均输出功率有着不同的影响，应根据所设计激光器性能的要求选择相应的输出耦合镜反射率。

在其它参量不变的条件下，取Cr4+∶YAG初始透过率T0=0.75，输出镜反射率R=70%，抽运光斑半径为100μm，Nd∶YAG中激光基模的半径为100μm。图3中给出了微片激光器的输出参量随抽运功率的变化曲线。由图3a、图3b可见，增大抽运功率给峰值功率与脉冲能量带来的具体影响，在抽运功率小于2W时，增大抽运功率的情况下，它们将随之呈急剧增大，当抽运功率超过2W后，它们将随之缓慢增大并逐渐趋于稳定；由图3c可见，激光脉冲重复频率受抽运功率的影响，在增大抽运功率时，它将随之线性增大，这是由于增大抽运功率，使增益介质中的反转粒子数与谐振腔中的光子数增加，光强变强，从而缩短了激光脉冲输出的间隔时间；而当抽运功率小于2W时，增大抽运功率，激光脉冲宽度将随之急剧减小，当抽运功率超过2W后，脉宽缓慢减小并逐渐趋于稳定，这主要是由于增大抽运功率时，使增益介质中的反转粒子数密度随之增加，提高了激光器的增益，从而导致激光器脉冲宽度减小。但是当抽运功率增大到一定值后，增益介质中的反转粒子数达到饱和，此时继续增加抽运功率并不会使增益介质中的反转粒子数进一步增加，所以脉冲宽度基本保持不变。因此这也意味着不能只依靠增加抽运功率来提高激光器的峰值功率和脉冲能量，但是在抽运功率处于一定范围时，提高抽运功率可提高脉冲能量与峰值功率，降低脉冲宽度。

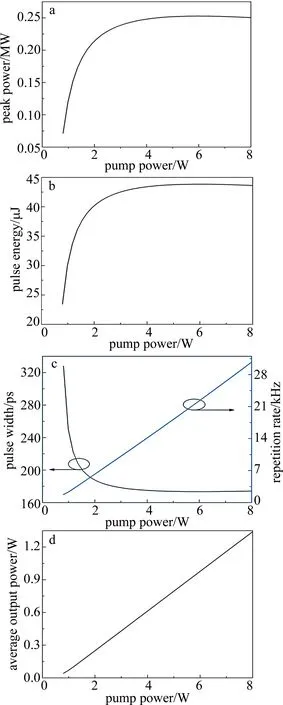
Fig.3 Relationship between pump power and other parameters

取抽运功率为4.5W，抽运光斑半径为100μm，Nd∶YAG中基模半径为100μm，保持其它参量不变仅改变Nd∶YAG长度的情况下，由图4b可见，随着Nd∶YAG长度的增加，单脉冲能量先增加后保持不变。由图4c可见，脉冲宽度随着Nd∶YAG厚度先减小后增加，Nd∶YAG为0.47mm时存在最小值为155ps，而重复频率则随着Nd∶YAG厚度的增加呈线性增加。由图4a可见，峰值功率随着Nd∶YAG厚度的增加先增加后减小，在Nd∶YAG为0.66mm时存在最大值为0.27MW。由图4d可见，激光器平均输出功率随Nd∶YAG厚度的增加而接近线性增加。为了增大激光器的峰值功率，减小脉冲宽度，应适当减小Nd∶YAG的厚度；为了提高激光器重复频率、平均输出功率则应适当增加Nd∶YAG的厚度。

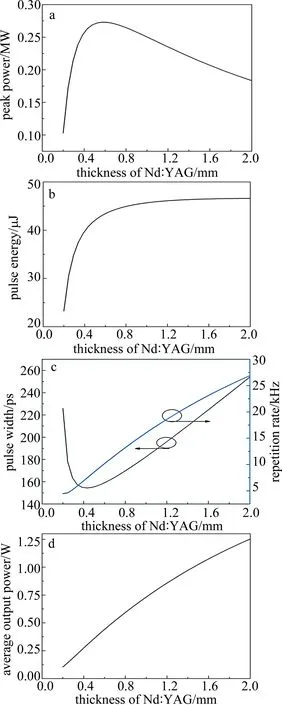
Fig.4 Relationship between the thickness of Nd∶YAG and other parameter

图5中给出了抽运功率为4.5W、抽运光斑半径为100μm、Cr4+∶YAG初始透过率T0=0.75、输出镜反射率R=70%、保持其它参量不变的情况下,激光器输出参量随Nd∶YAG晶体中激光基模半径的变化关系。由图5a、图5b、图5c可见，随着Nd∶YAG中激光基模半径的增加，峰值功率、脉冲能量、平均输出呈二次方增加，这是由于随着激光基模半径的增加，谐振腔中光子数会随之增加，因此，提高了激光器的峰值功率；脉冲宽度近似为脉冲能与峰值功率的比值，平均输出功率为脉冲能量与重复频率的乘积，由于脉冲宽度和重复频率与激光基模半径无关，所以两者在激光基模半径变化时保持不变，所以脉冲能量与平均输出功率也呈二次方增加。

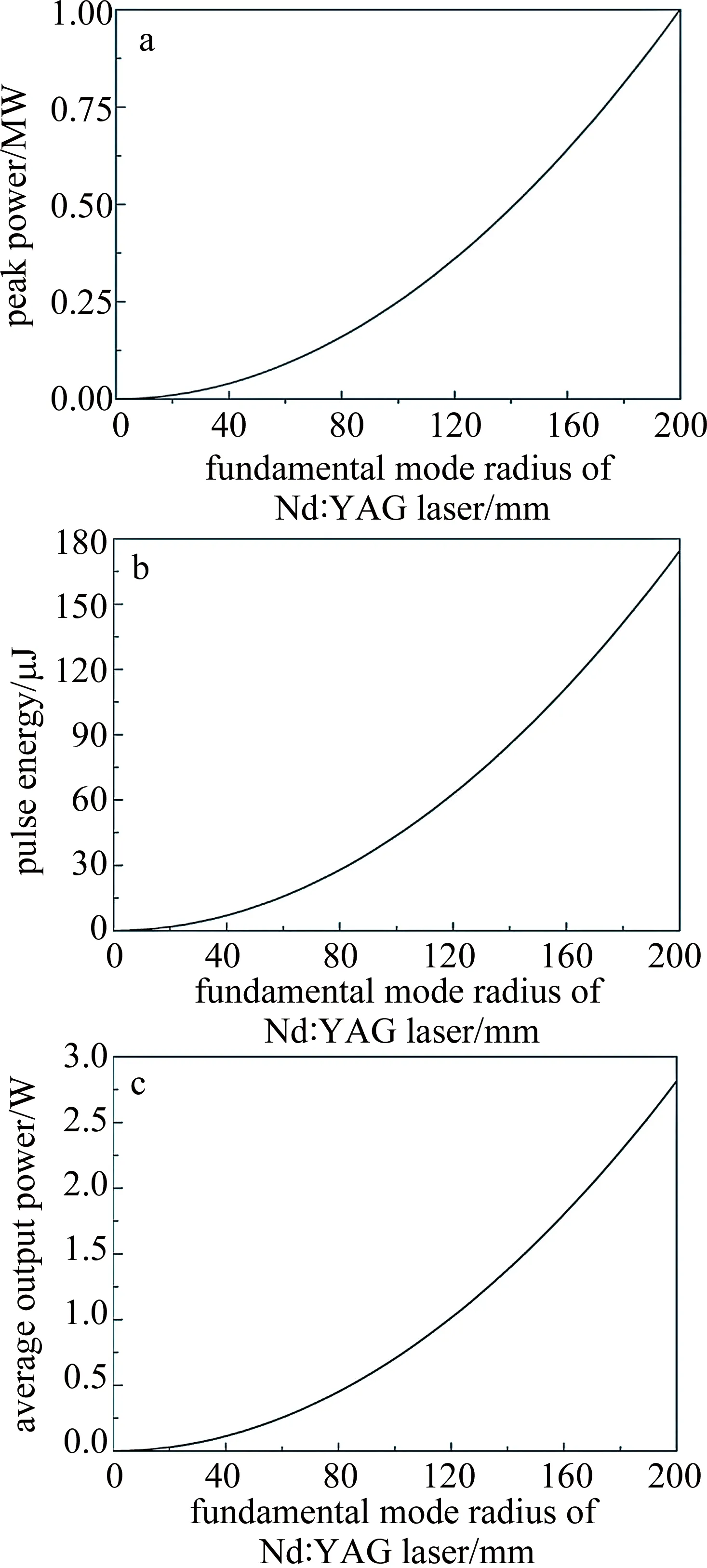
Fig.5 Relationship between laser fundamental mode radius of Nd∶YAG and other parameter

通过上述分析，选取所设计激光器的相关参量。取Nd∶YAG的长度为1mm，Cr4+∶YAG的长度为1.5mm，抽运光斑半径为100μm，Cr4+∶YAG的初始透过率为0.75，Nd∶YAG中激光基模半径为100μm，输出镜的反射率R=70%。最终利用上述设计参量，在抽运功率为4.5W下获得了微片激光器平均输出功率为0.7W，脉冲宽度为174ps，脉冲能量为43.6μJ，峰值功率为0.25MW，重复频率为16.1kHz的理论输出参量。

3 结 论

通过对加入抽运项以及可饱和吸收体激发态吸收的被动调Q速率方程组进行数值求解，分析了不同因素对激光器输出参量的影响。分析结果表明，对于Nd∶YAG/Cr4+∶YAG微片激光器，通过适当增加抽运速率、增益介质中激光基模半径、Nd∶YAG的厚度，以及减小输出耦合镜反射率和可饱和吸收体的初始透过率可提高激光器的峰值功率和脉冲能量；并且存在最佳输出镜反射率使平均输出功率有最大值。通过改变Nd∶YAG/Cr4+∶YAG微片激光器结构参量对其输出特性进行数值仿真，以便直观地看到输出特性随各结构参量的改变，这对于此类激光器在输出性能方面的提升具有重要意义。