顾及病态的融合解算坐标转换模型研究

孟庭伟

(南京市测绘勘察研究院股份有限公司，江苏 南京 210019)

1 引 言

坐标转换广泛应用于测量行业中，其实质是利用公共点的两套坐标及非公共点的第一套坐标值推估第二套坐标值。三维基准转换通常采用7参数(3个平移参数，3个旋转参数，1个尺度因子)进行坐标转换，先用公共点坐标解算转换参数，再利用转换参数转换非公共点坐标。

空间直角坐标转换的模型与方法众多，常用的三维基准转换模型有Bursa模型、Molodensky模型、武测模型等，其中，Bursa模型适用于大范围(>1002km)、小角度(3°以内)的坐标转换，对于小范围区域，公共点间隔较小，平移参数与旋转参数具有复共线性，导致法方程矩阵病态，从而导致解算的平移参数值与旋转参数值有较大的误差[1，2]。坐标重心化减小了参与计算的坐标数值，有效地弱化平移参数与旋转参数的强相关性，降低了法方程矩阵的严重病态性，增强了数值计算的可靠性[3]。Tikhonow提出的正则化方法是解算病态方程的有效方法，小范围公共点主要引起平移参数的解不稳定，对平移参数进行正则化处理，提高外围点坐标的转换精度[4]。对于大旋转角的坐标转换已有大量研究，游为等直接从三维直接坐标转换的非线性模型出发，采用基于同伦连续思想的Li-Yorke算法最优解7个转换参数，该方法虽然适用于大旋转角转换，但计算过程比较复杂[5]。本文提出顾及病态的融合解算坐标转换模型，有效地解决了Bursa坐标转换模型病态性问题，通过算例分析验证该算法适用于任意旋转角度的空间直角坐标转换。

2 三维空间直角坐标转换模型

空间直角坐标转换模型：

(1)

(2)

式中，∈x、∈y、∈z为空间直角坐标变化的三个旋转角，由于三个坐标系的旋转角度小，故取cos∈x=cos∈y=cos∈z=1，sin∈x=∈x，sin∈y=∈y，sin∈z=∈z同时忽略二阶以上的微小量。

根据最小二乘原理，利用多个公共点信息进行平差解算转换参数。

(3)

其线性方程为：

AX=L

(4)

由于坐标转换中各观测值相互独立，故可设权阵P=I，根据最小二乘原理得：

X=(ATPA)-1ATPL

(5)

V=AX-L

(6)

其单位权中误差为：

(7)

式中，n为公共点的个数。

3 融合解算模型

3.1 坐标重心化

由于已知公共点坐标含有粗差，观测向量误差对解向量误差的影响与法方程系数阵的条件数成正比，当法方程系数阵的条件数Cond(ATPA)=‖ATPA‖‖(ATPA)-1‖(≥1000)很大时，很小的观测误差引起解得的未知参数向量有很大的误差，转换参数精度低，导致转换模型病态，经坐标转换的目标坐标误差较大。因此，将原始坐标系与目标坐标系中的坐标值分别进行重心化，使得参与计算的数值变小，其坐标系的原点平移到点集的重心，法方程矩阵为对角阵，弱化平移参数与旋转参数之间的复共线性，降低法方程的病态性。

(8)

式中，(Xi重，Yi重，Zi重)为坐标系i(i=1，2)公共点的重心坐标，利用重心坐标求出各个公共点的重心坐标(XZij，YZij，ZZij)。

(9)

通过坐标重心化得到两组新的公共点坐标，使得参与计算的数值变小，将两组新的坐标值带入到式(6)，组成新的误差方程。

3.2 正则化

坐标重心化弱化了平移参数与旋转参数的复共线性，但并没有完全解决转换模型的病态问题，法方程系数阵ATPA的条件数仍很大，为了得到更加稳定的解，采用Tikhonov正则化处理思想，引入正则化参数，以式(10)取得极小值为准则：

(10)

式中，Φα为Tikhonov光滑函数，α为正则化参数，‖·‖为向量的二范数，将式(5)中系数矩阵叠加正则化参数α，满足条件α>0，式(10)存在唯一的极小值，其相应的解为：

Xα=(ATPA+αIn)-1ATPL

式中，In为n阶单位阵，若已知正则化参数α，则可解算未知参数的正则化估值Xα。由于正则化解是有偏的，用均方误差评定精度，其偏差△Xα与均方误差MSE(Xα)为：

(11)

均方误差由观测误差引起的估值误差和正则化引起的估值误差两部分组成，合理的正则化参数平衡这两类误差，使两类误差值之和最小。因此，正则化参数不仅与系数矩阵A有关，而且与观测值的精度有关。

(12)

只对平移参数进行正则化处理，引入正则化矩阵R，其相应的计算公式为：

Xα=(ATPA+αR)-1ATPL

(13)

(14)

求解正则化参数的准则是均方误差最小，即均方误差的迹取极小值：

Trance(MSE(Xα))=min

(15)

采用L-曲线法确定α值。

3.3 罗德里格矩阵

罗德里格矩阵由反对称矩阵构建，引入一个具有3个独立元素的反对称矩阵S。

(16)

则R=(I+S)(I-S)-1为正交矩阵，其中I为3阶单位矩阵。

(17)

利用罗德里格矩阵解算旋转参数，尺度参数可通过两个公共点在不同坐标系下的欧式距离之比得到，当含有的公共点个数较多时，可分别求取各点距离之比，取其均值作为尺度因子。

(18)

选取两个公共点带入式(1)作差，消去平移参数。

(19)

由于R为反对称矩阵，根据R与罗德里格矩阵S的关系，可得：

(20)

将两套坐标系下的公共点3带入到式(1)，与公共点1代入式(1)的结果作差，将结果与式(20)联立。

(21)

式中，X2ji=X2j-X2i，Y2ji=Y2j-Y2i，Z2ji=Z2j-Z2i，X1ji=X1j-X1i，Y1ji=Y1j-Y1i，Z1ji=Z1j-Z1i，X2ki=X2k-X2i，Y2ki=Y2k-Y2i，Z2ki=Z2k-Z2i，运用最小二乘原理得到反对称矩阵参数a、b、c。

将引入正则化参数解算的平移参数，罗德里格矩阵解算的旋转参数与尺度因子带入式(1)，解算非公共点在目标坐标系下的坐标。

4 算例分析

根据旋转角的大小不同，将实验数据分为两组，小旋转角的公共点坐标作为一组数据，大旋转角的公共点坐标作为另一组数据，两组数据如表1和表3所示。分别选取表1与表3中的点1、2、3作为解算旋转参数的公共点，分别用Bursa模型、坐标重心化模型与融合解算模型解算转换参数，点4、5的原始坐标数据利用所得转换参数解算目标数据，验证三种模型的转换精度如表2与表4所示。

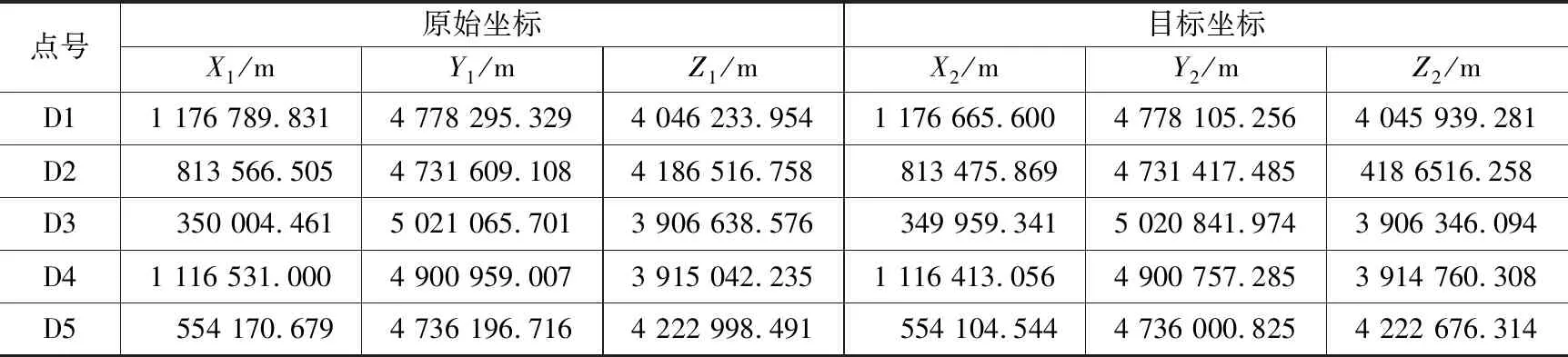
小旋转角的原始坐标与目标坐标 表1

中误差精度对比分析 表2

大旋转角的原始坐标与目标坐标 表3

中误差精度对比分析 表4

5 结 论

本文分别利用小旋转角与大旋转角数据进行算例分析，由于平移参数与旋转参数之间存在复共线性，顾及病态的融合解算坐标转换模型首先进行坐标重心化转换模型减小了参与计算的数值，有效弱化了参数之间的强相关性，分两步解算平移参数、旋转参数及尺度因子，改善了Bursa模型的病态性，罗德里格矩阵无须对旋转参数进行线性化，具有高的转换精度，适用于任意范围与角度的空间直角坐标转换。