浅谈数学建模在探究小学“工程问题”中的应用

■厦门市故宫小学 何雪琴

说起“工程问题”也许大家脑海里还会有蓄水池水管注水和放水的困惑，由于外界的争议，“工程问题”曾退出小学数学的舞台，2011年颁布新课程标准后，重新修订教科书，2013年数学人教版教科书又新加入“工程问题”。这一退一进之间，彰显“工程问题”的数学价值。它是“分数除法”这一单元的最后一个例题，是学生系统学习分数相关知识后对分数认识的又一次升华，是体现分数抽象性的最好素材，也是用“假设法解决问题”最典型的例子，更是渗透模型思想的活动载体。通过课前调查，我发现有很多同学已经会用“1”作总量进行列式计算了（看过书或课外学过）。然而，学生会根据模型列式解答，不代表他们都已真正理解模型。在学生暴露学情后，我们将课堂重心转向引导学生把现实问题“模型化”的过程，开启对工程问题的深度探索。

一、“充分阅读，合理估测”触摸建模起点

第一次教学这个例题，教学探究部分我们设计的第一环节重点是“阅读信息，大胆猜想”，旨在深度阅读为建模做充分的准备。问题情境：一队单独修需要12天修完，二队单独修需要18天，那两队合修，需要多少天呢？面对这个问题，教师可以引导学生思考一队单独修可以12天完成，从而可以判断出，他们合作修的天数一定小于12天。当然，这只是我们的猜想，数学不能光靠猜想，必须还要通过正确的方法来验证。试想把“猜想”升级为“估测”，估测的思维过程是激活原有的知识、经验与实际问题结合起来，不断假设或推翻设想的高级思维活动。“估测”作为算术估计的组成部分之一，是国际基础数学教育改革重要的内容。在第二次教学时我们把“大胆猜测”改为“合理估测”，尝试引导学生在“合理估测”中对“工效”“工作总量”“工作时间”“效率”进行理解，为数学建模做充分的准备。学生从具体情境中抽象出数学问题，发现和提出问题，是数学建模的起点。到第二次教学这个环节时，我的重心改为“充分阅读，合理估测”。学生的合理估测离“数学建模”更进一步。

还是同样的情境，如果给你一条数轴0——6——12根据你的估测两队合作完成的天数大约在数轴的什么位置？说说你的理由。这又进入了引导学生估算环节。

二、“大胆假设、尝试解决”夯实建模基础

在“充分阅读，合理估测”的铺垫下鼓励学生自主探究“合作需要几天完成呢？”自己尝试解决后学生汇报环节非常精彩，据统计学生的假设法就有十几种。假设法大致分为三类：假设这条路的总长是12、18的公倍数的（36米、180米、360米……）占全班人数60%；假设这题路为字母（a米、x米）占全班人数的4%，假设为这条路的总路程为“1”占全班人数的25%。归纳推理是特殊情况下作出一般结论，是一种基于推断的推理。在小学数学中我们使用最多的是简单枚举推理，从个别或者特殊事物出发概括出结论的思维方法，学生假设这条路的总长不同，计算结果相同，那是不是无论这条路的总长设成多少，得到的答案都一样？变换几个不是12和18的公倍数的数试试后学生又引入字母，让字母参与运算，得到的结论更加严谨，更有说服力。

三、“交流讨论，自主抽象”提取数学模型

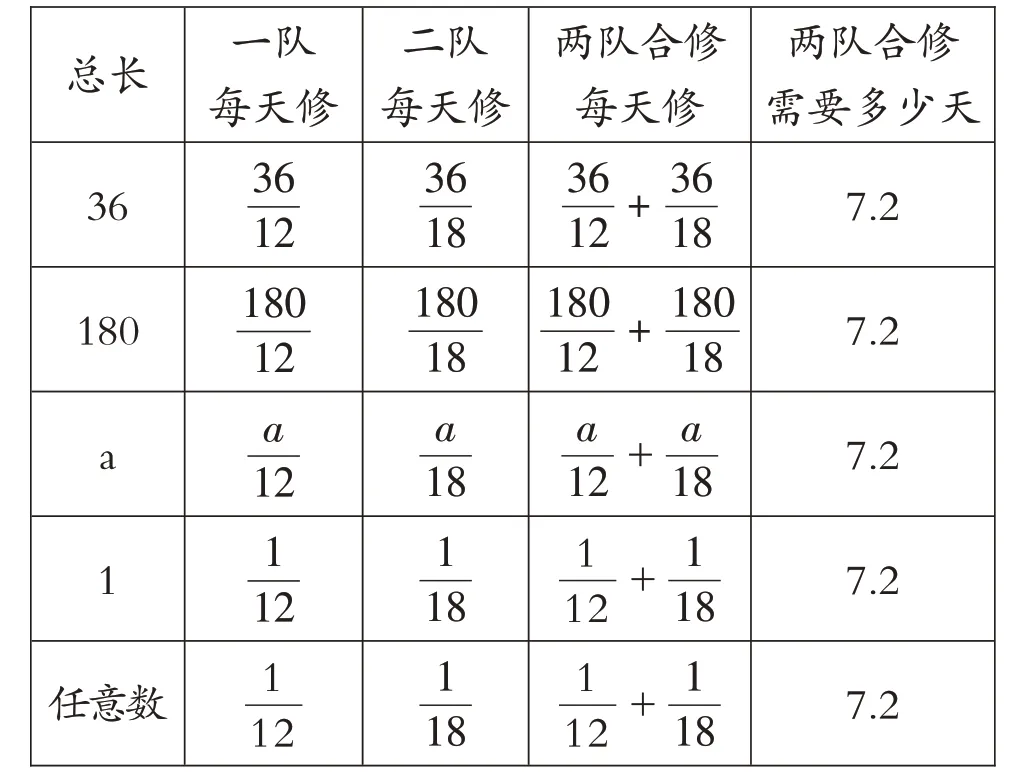
在学生汇报后根据学生反馈把典型数据通过课件整理成表格的形式，通过解决办法的观察，从表格数据学生在“变中找不变”中提取数学模型，在表格整理数据之后设计线段图帮助学生抽象解题题结构。在学生观察数据并分析模型背后的算理的基础上，教师逐渐引导学生总结解题模型。数学模型是一种数学形式表达，我们的任务是求解模型，在求解模型过程中让学生理解数学模型的意义，也就是理解数学知识。建模过程是学生获得知识技能的过程也是思想方法等经验积累的过程，在这个环节中，学生通过观察、分析、抽象、概括等数学活动完成模式抽象，把复杂的实际问题简单化，抽象成合理的数学结构。

四、“举一反三，触类旁通”应用数学模型

在数学教学中，可利用具体实例说明，通过实例来帮助理解抽象的数学内容，通过典型的问题解决带动相关问题的解决，由一个到一类，触类旁通应用所得到的数学模型去解决问题。教师可以在习题中安排运输问题、行程问题、泄洪问题作为抽象数量关系的现实载体，通过解决此类问题、透过各种现实表象，找出隐藏其后的数学模型，将模型解答和现实生活进行对照检验，根据检验结果对解答进行修订，得到满足现实问题的优化解答。数学模型是一种数学表达方式，并不能解决问题，如果一味地用所获的数学结构去解决实际问题，那么生搬硬套的“套路化”的解题会限制了学生的思维。为了化解“模型化”后“套路化”解题的矛盾，我们设计这样的课后练习，通过对练习的辨析进一步理解数学模型的意义，活用数学模型解决同类问题，加深对数学结构的理解。例如同类型题目，一条公路，甲队3天修了，乙队4天修两队合修几天修全长的练习的编排给我们解释理解模型提供很好素材，模型背后的数理是：工作总量÷工作效率=工作时间；工作总量÷工效和=合作时间。通过练习对已经学得的数学模型在不同情境下进一步应用，在应用过程中，促进学生把学习的知识、学习的能力、感悟到的思想方法进行内化，成为学生的数学素养。

“工程问题”重新编排到新人教版教材应避免不断变式深挖，教学的重点转向通过例题的学习积累学习经验，让学生形成发现问题、分析问题、解决问题的能力，会找变中有不变背后的数学模型。模型思想的教学不是教知识点，而是渗透模型思想，需要经历一个复杂漫长的积累领悟的过程。我们旨在建模和实际应用过程中促进学生能力发展。