基于虚拟同步机电力电子变压器直流电压平衡控制策略
宋平岗, 杨声弟, 钟润金, 郑雅芝, 江志强, 周鹏辉
(华东交通大学电气与自动化工程学院, 南昌 330033)
随着电力机车传动技术迅速发展,以工频变压器为主的传统电力牵引传动系统难以满足电力机车面向未来轻量化智能化发展需求,基于现代电力电子技术的发展提出一种新型的电力电子变压器(power electronic transformer,PET)传动系统,相关成果也不断地推出[1-3]。与传统牵引变压器系统相比,该系统不仅体积小、重量轻,而且可控性高,可以更好地实现电能变换、隔离、传递、模块化等功能[4-5]。
受限于功率器件的物理特性,在中高压大容量领域,通常需要采用多个功率单元进行串并联从而提高系统功率等级。由于各级功率单元电路存在参数不同等因素,从而导致PET整流侧直流电压不平衡,降低整个系统效率以及不稳定等一系列不利影响[6]。因此,稳定直流侧电压平衡是整个系统稳定运行的前提。现重点分析电力电子变压器网侧级联H桥直流电容电压平衡控制策略。
文献[7-9]提出了d-q电流解耦的控制策略,通过计算出网侧有功分量值,无功采用闭环调节,通过一定控制环节得到控制信号,再通过d-q反变换可以得到调制信号。采用比例-积分控制器以及复杂的坐标变换和反变换,因此限制采用该调制策略时系统的通用性。文献[10-12]采用瞬态电流控制策略,引入网侧交流相位,实现无相位差整流,实现单位功率运行。文献[13]提出采用后级DC-DC进行功率补偿控制策略,该控制策略本质上是将后级的DC-DC进行前馈均功率控制,保证后级每级DC-DC功率平衡,从而在参数一致的情况下保证级联H桥整流器(cascaded H-bridge rectifier, CHBR)的输出电容电压稳定。
针对上述文献所提电容电压平衡控制策略进行改进。采用载波移相调制算法,在整流侧注入惯性环节和阻尼系数,提高系统的动态性能[14]。进一步通过设计直流电容电压选择控制器,作为各级调制信号补偿,从而维持输出每级直流电压平衡。最后,通过上述虚拟同步机下载波移相调制(carrier phase shifting-sinusoidal pulse width modulated, CPS-SPWM)脉冲补偿式电容电压平衡控制策略进行仿真,验证所提策略的有效性。
1 电力电子变压器拓扑结构
1.1 PET拓扑
采用的电力电子变压器拓扑结构如图1所示,采用典型三级结构;其中,输入级采用级联H桥整流(CHBR)拓扑结构;中间级隔离级采用双有源全桥(dual active bridge,DAB)变换器结构;并且各级变换器相互独立,输入级采用个功率单元独立输出,输出级采用各单元直流母线并入后逆变输出的结构。

图1 电力电子变压器拓扑结构Fig.1 Power electronic traction transformer topology
采用该拓扑结构的电力电子变压器基本是依照层级相互依次进行电能变换,即输入网侧的交流-直流变换、中间层隔离级DAB直流-直流能量传递,输出侧直流-交流变换输出。每级变换环节相互独立,彼此之间互为激励或为负载。因此可以单独对每个电能变换环节的控制策略进行分析[15]。
1.2 基于虚拟同步机的CHBR模型
N级联电力电子变压器网侧整流拓扑结构框图如图2所示,该拓扑由N级全桥结构功率单元串联,只需增加或减少相应的H桥单元,为了便于分析,可以单独对单个H桥两电平结构进行分析。

us表示牵引传动系统的牵引电压;is表示网侧电流;uab为节点电压;udc为直流链路电压;L为网侧等效电感;编号S11~S14分别表示4个功率开关器件;C为直流侧储能电容;R为直流侧等效电阻;id为直流侧电流;ir为直流侧负载电流; R为直流侧等效电阻图2 CHBR拓扑结构框图Fig.2 CHBR topology block diagram
根据基尔霍夫定律,可以得出单级等效H桥整流器数学模型为

(1)
文献[16]引入直流链路电容的动态方程实现同步机原理如式(2)所示,因此可以将CHBR变换器一侧等效为虚拟同步机。

(2)
式(2)中:ω为同步电机的机械角速度;ω0为电网额定角速度;KT为调节系数;KJ为阻尼系数;KD为转动惯量;udc_ref为直流链路参考电压。同时由同步发电机的机械方程和电磁方程可知:

(3)
式(3)中:J同步电机的转动惯量;Te为同步电机的电磁转矩;Tm机械转矩;Dp为同步电机的阻尼系数。
由同步机原理进一步可以得到CHBR虚拟同步机电磁方程为

(4)
式(4)中:eu为同步机内电势;us为同步机端电压;r和L分别表示定子的等效内阻和电感
由式(3)可知,电力电子变压器的网侧级联H桥整流单元,可以引入虚拟同步发电机技术通过一定控制策略,从而实现直流电容电压的平衡控制。
1.3 直流电容电压不平衡分析
由文献[17-18]分析结果可知,在载波移相调制策略上所产生的直流侧电容电压不平衡是必然存在的,并且分析了采用载波移相调制所产生不平衡机理。文献[19]分析直流电容器大小不会影响稳态下的平衡问题。
在理想条件下,如果每个单元参数相同且单元内的器件参数均一致,控制器所发出的PWM不存在延时,那么直流电容电压将会保持平衡。但在实际系统中,是难以保证参数一致,而延时是可以通过一定的补偿改善。式(5)可以说明,直流电容电压不平衡的主要原因是电容器直流能量的差异造成,而电容器能量差异主要可分为两类;能量通过H桥电路在直流电容与牵引网之间的交换。由H桥电路控制能量流向;系统中损耗以及电容器等效参数的不同与负载不同所引起的直流电容电压不平衡。

(5)
式(5)中:Edc为电容能量。
在电力电子变压器中,级联H桥整流器的能量是单向流动即从牵引网通过H桥变换器流向电容器。因此重点分析电容等效参数以及负载不同所引起的不平衡问题。图3所示为直流环节等效电路模型。

ui为输入电压;i为输入电流; Resr为等效串联阻抗;uC为电容电压;uesr为等效串联阻抗电压;iC为电容电流;ir为负载电流;R为等效负载;udc为负载电压图3 直流环节等效电路模型Fig.3 DC link equivalent circuit model
由基尔霍夫定律可以得到

(6)

(7)
整理得

(8)
由式(8)可以得出,电容等效参数阻抗将会影响电容电压波动,直流侧负载的波动也将对直流电容电压产生影响。
2 虚拟同步控制策略
2.1 基于虚拟同步机控制策略
基于虚拟同步机下的电力电子变压器CHBR直流电容电压平衡控制框图如图4所示。
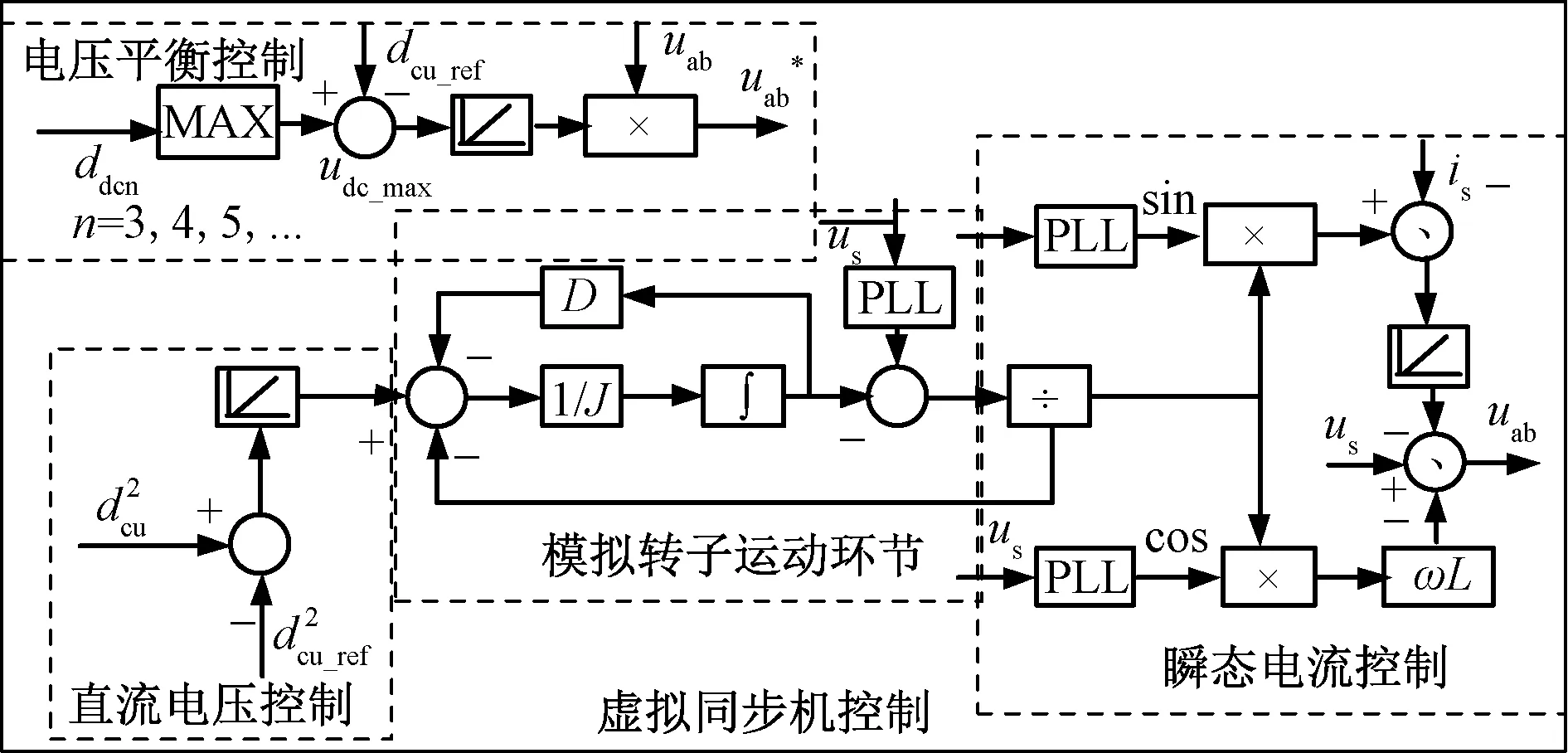
图4 直流电容电压平衡控制系统框图Fig.4 DC capacitor voltage balance control system block diagram

2.2 虚拟同步机参数对系统特性的影响
虚拟同步机功率内环可以等效为一个二阶系统[20]。系统传递函数框图如图5所示,虚拟同步机环节进一步分析系统稳定性。

PM为输入功率;PC输出功率;Z为系统阻抗;s为积分符号图5 系统闭环控制图Fig.5 System closed loop control block diagram
根据图5可以计算出闭虚拟同步机闭环传递函数Gvsg(s)为
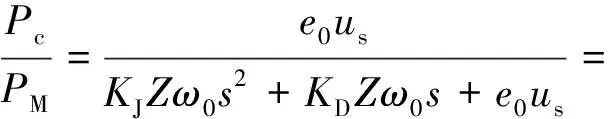

(9)
可以得到阻尼系数ξ和自然剪切频率ωn为
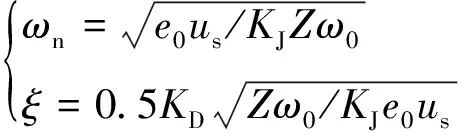
(10)
同步机一般工作在欠阻尼工作状态,因此取0<ξ<1误差范围±2%可以得到系统超调量Mp和调节时间ts,即

(11)
虚拟同步机等效二阶系统动态能由转动惯量KJ和阻尼系数KD决定,由式(11)可知,当KJ恒定时,越小,超调量越小,调节时间ts越短,当KD恒定时,越大,超调量越长,调节时间ts越长。转动惯量和阻尼参数可在一定范围内调整。
由式(9)~式(11)可以得到二阶系统的闭环极点表达式,即特征根方程式:
KJZωns2+KDZωns+e0us=0
(12)
解得方程根s1、s2分别为
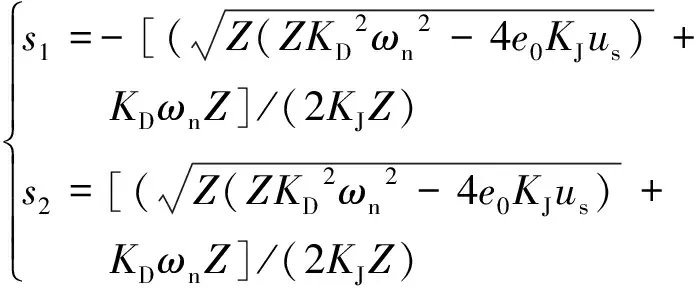
(13)
从式(13)特征根可以得到,随着不同,其特征根和相应的瞬态响应差异也很大。
综上所述,对于一个确定的同步发电机,转动惯量KJ和KD几乎是恒定的,对系统不会造成很大波动,对于虚拟同步机控制而言,虚拟的转动惯量和阻尼系数作为系统控制参数,在满足系统稳定性和动态性时,KJ和KD可以根据实际系统进行调整,综合系统响应以及动态性能做出选择。
2.3 系统稳定性
虚拟同步机环节可以等效为一个二阶系统。根据上述模型可以得到单个H桥功率单元的直流参考电压udc _ref指令值与实际直流侧电容电压值udc的闭环传递函数,如式(14)所示,以单个H桥功率单元建立直流电容电压平衡控制模型如图6所示。

图6 单H桥控制闭环控制框图Fig.6 Single H-bridge control closed-loop control block diagram
系统闭环传递函数Φ(s)为

(14)
通道环节G(s)为

(15)
整理得

(16)
式中:kp为PI控制器比例控制参数;ki为PI控制器积分控制参数。参考最优控制理论以阻尼比ξ=0.707和剪切频率ωn=20 rad/s为虚拟同步机控制器动态性能指标进行分析代入式(9)可求得相应转动惯量和阻尼系数。综合考虑系统性能,因此首先固定取KD=5时,KJ=0.02、0.04、0.08、0.1;同时KJ=0.02时,KD=5、6、7、10;得到系统闭环时域特性bode图,如图7所示;系统的稳定裕度基本维持不变,相角裕度呈微弱变化。因此从bode图中可以看出,在一定范围内取值并未对系统造成严重的破坏。
3 仿真结果与分析
3.1 仿真验证
为不失一般性,采用三级联H桥进行仿真验证。仿真参数如表1所示。
对2.2节所提虚拟同步机参数对系统影响进行仿真验证,首先KD=5取恒定值,分别对KJ=0.02、0.2、0.4、0.6、0.8进行仿真,以及当KJ=0.02取恒定值时,分别取KD=5、8、10、12、15时的阶跃响应波形如图8所示,图中P为系统输出功率。

图7 系统时域特性图Fig.7 system time domain characteristic map

表1 仿真参数

图8 系统阶跃响应Fig.8 System step response
由图8(a)可知,在KD一定时,系统阶跃响应时超调量Mp随着KJ的增大而增大,同时上升时间与调节时间tP也随着KJ的增大而增大。由图8(b)可知,当KJ一定时,系统阶跃响应的超调量Mp随着KD的增大而减小,同时上升时间却随着KD的增大而增大,调节时间tp相应减小,因此验证2.2节所分析系统参数的影响,同时通过2.2节中的分析知,KD、KJ的变化同时也会对系统带宽产生影响,因此对于KJ、KD的选取也需综合考虑整体系统的性能以及从稳定性角度做出合理选择。
对采用SPWM与 CPS-SPWM调制策略进行仿真分析,验证所用调制算法优越性。仿真结果如图9所示,在B区为采用CPS-SPWM调制时的牵引网等效电感电压波形,A区为采用SPWM调制时牵引网等效电感电压波形,牵引网侧的电感电压为2N+1电平数,使得电力电子变压器能够适应低调制下的工作,并且实现低次谐波的相互抵消从而获得良好的谐波特性[21]。

图9 等效电感电压波形Fig.9 Equivalent inductance voltage waveform
而由于级联参数与调制算法的差异,将会带来网侧电流大量谐产生,同样验证采用CPS-SPWM调制策略对电流谐波的抑制如图10所示。采用SPWM调制时取 1 s之后的5个周期电流进行快速傅里叶变换(fast fourier transform,FFT)分析,结果如图10(a)所示,总谐波失真(total harmonic distortion,THD)THD=5.88%,同时对1 s前的5个周期电流进行FFT谐波采样分析,如图10(b)所示,THD=2.21%,有效地抑制谐波含量。传统系统可能会因为入网侧的电流谐波含量较大,在通过一级级变流器而导致谐波大量产生,谐波含量小这对于牵引传动系统尤为关键。
对虚拟同步机下直流电容电压平衡控制策略进行仿真验证,分别取R1=45 Ω、R2=50 Ω、R3=55 Ω,如图11所示,A区为未加入平衡控制算法下的仿真输出,B区为加入平衡控制算法下的仿真输出,从图中的右下局部放大小图中可以看出,CHBR的三端输出逐渐趋向于参考电压。
对不同电容等效参数进行验证,电容值取C=2 mF等效阻抗Resf1=0.01 Ω、Resf2=0.02 Ω、Resf3=0.05 Ω,如图12所示,A区为未加入平衡控制算法下的仿真输出,B区加入平衡控制算法下的仿真输出,从图中的右下局部放大小图中可以看出,CHBR的三端输出逐渐趋向于参考电压。

图10 不同调制算法谐波分析Fig.10 Harmonic analysis of different modulation algorithms

图11 不同负载直流电容电压波形图Fig.11 Different load DC capacitor voltage waveforms

图12 不同直流电容等效阻抗输出电压波形图Fig.12 Waveform diagram of equivalent impedance output voltage of different DC capacitors
最后进行负载的突变仿真验证,如图13所示,在仿真进行1 s时切入不同负载,由原先取30 Ω突变为60 Ω。从图13中可以看出,虚拟同步机下的控制CHBR三级基本都保持在参考电压附近,并且电容电压输出呈现良好的过渡,如图中左小图所示,同样在负载突变时,可以看出,过度较为平滑,并未呈现出较大冲击,平缓过渡到参数值附近最后CHBR的三端输出逐渐趋向于参考电压。进一步验证了所提控制策略的有效性。
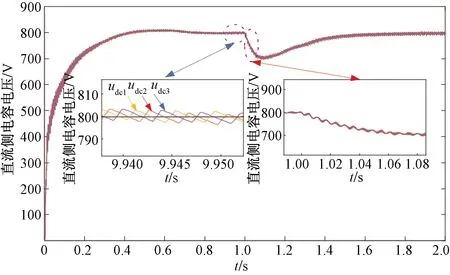
图13 负载突变输出电压波形图Fig.13 Load abrupt output voltage waveform
3.2 仿真结果分析
以3级联CHBR为例,对上述分析进行仿真验证,针对不同的调制算法、电容等效阻抗不同以及直流侧负载不同和负载突变等导致直流电压不平衡因素进行仿真,所提控制策略较好地实现CHBR直流侧电容电压平衡,所提控制策略极大地简化了控制系统设计。
4 结论
基于虚拟同步机理论,提出了电力电子变压器网侧整流端直流电容电压平衡控制策略。并分别从控制与调制两个方面实现直流电容电压平衡进行分析与仿真验证。在瞬态电流控制下克服了由传统CHBR带来的控制策略复杂,并且验证采用SPWM与CPS-SPWM调制时输出电流电压特性。所提控制结构简单,可靠、稳定,为PET传统系统在中高压轨道电力机车牵引传动系统提供了可行性方案分析。

