支持向量机回归分析法在地铁车站基坑沉降监测中的应用

唐治海

(浙江省工程勘察设计院集团有限公司，浙江 杭州 315031)

随着社会经济发展的加快，各大城市都紧锣密鼓地开展地铁建设，鉴于地铁项目的地下特殊性，其基坑安全尤为重要[1-5]。整个开挖与施工过程中，持续的基坑沉降监测可以有效地保证施工安全。基坑沉降预测一直是相关工作者的研究重点，很多文献在回归分析、灰色模型、指数平滑模型等方面对基坑预测做出了研究，获得了很多有益成果[6-8]。但数学模型限制于模型自身局限性，不能进行数据特点学习，拟合效果不尽人意。具有学习机制的支持向量机回归法能够进行有效学习输入数据序列特点，从而对未来数据进行高精度预测，可以适用于基坑沉降预测[9-13]。本文从支持向量机核函数入手，介绍基坑沉降预测过程，开展相关讨论。

1 支持向量机基本思想与核函数

支持向量机的基本思想是，选择适合于数据特点的核函数，通过核函数将输入向量映射到高维特征空间，在此空间中构建最佳分类超平面，从而将空间中的数据点分离。最佳分类超平面必须使分类间隔最大，数据点距离超平面距离尽可能远，才能保证训练错误最小。如图1所示，在低维空间中做相关表示，H代表最佳分类超平面(在低维空间中是线)，推广到高维空间即为最优分类面。支持向量机结构如图2所示。

图1 低维空间的最佳分类超平面

图2 支持向量机结构

主要核函数有以下三种：

(1)多项式核函数表达式见式(1)：

K(x,x′)=[(x·x′)+c]p,c≥0,p=1,2,…

(1)

式中，p为多项式阶次，所得是p阶多项式分类器；K(x,x′)为核函数；(x·x′)为内积运算。

(2)高斯径向基核函数表达式见式(2)：

(2)

式中，σ为可控参数，选择不同的σ参数值，相应的分类面会有很大差别。

(3)Sigmoid核函数

K(x,x′)=tanh[u(x,x′)-r]

(3)

式中,u、r为常数；tanh为双曲正切函数。

Sigmoid核函数有两个参数，而高斯径向基核函数只有一个可控参数σ，本文选择核函数时通常选择RBF作为核函数。

2 沉降预测模型与精度评定

2.1 沉降预测模型

变形预测目标函数见式(4)：

y=f(x)=ω·Φ(x)+b

(4)

式中，Φ(x)为非线性映射。待求目标函数表示见式(5)：

(5)

(6)

预测模型训练过程如图3所示。

图3 模型训练步骤

2.2 模型评定指标

(1)平均绝对百分比误差：

(7)

(2)均方根误差：

(8)

(3)平均绝对误差：

(9)

3 工程概况与数据预处理

3.1 工程概况

某地铁车站，拟建基坑深度约11.2 m，地下二层、地上四层，基础形式为筏板基础，主体车库基坑面积为15 126.5 m2，基坑长约135.8 m，宽约110.7 m，深度约为11.2 m，坡道基坑面积约为914.3 m2，深度为1.25～5.1 m，基坑总体平面图如图4所示。本次采用数据为基坑北8号点沉降数据，已有该点2009年11月21日～2011年10月29日观测的64期沉降数据，其中后8期数据用于预测评估，其余数据用于建模。

图4 基坑整体平面图

3.2 数据预处理

将每一期累计时间取一次自然对数，累计沉降值进行归一化处理，将其值化归到[-1,1]区间内，公式见式(10)。

(10)

xi=xi′(xmax-xmin)+xmin

(11)

本实例中，取xmin=2 mm，xmax=52 mm，对原始累计沉降量进行归一化处理。支持向量机回归设定三个参数：惩罚因子C、RBF核参数σ、不敏感损失函数ε。经过反复验证，得到三个参数的最终经验值为：C=20，σ=10，ε=0.001。

4 预测结果

8号点累计沉降预测值与实测值对比图如图5所示，后8期预测放大对比图如图6所示。

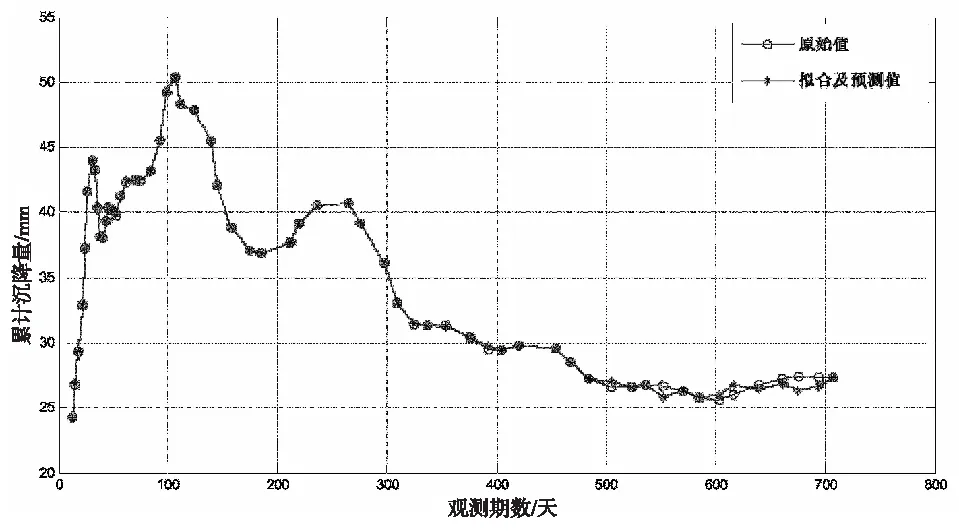
图5 预测拟合值与实测值对比图

图6 后8期预测值与实测值对比图

由图5可知，支持向量机拟合效果精度比较高，后8期的预测值虽有一定偏差，但都在误差允许范围内。最大拟合误差为0.806 mm，最小拟合误差为0.000 mm，最大预测误差为1.056 mm，最小预测误差为0.018 mm。

残差对比图如图7所示，后8期预测数据残差放大对比图如图8所示，后8期预测成果表如表1所示。

表1 后8期预测成果表/mm

图7 预测残差图

图8 后8期预测残差图

根据预测成果进行精度评定如下：

平均绝对百分比误差：

均方根误差:

平均绝对误差：

5 结 论

通过对64期已知数据计算发现，支持向量机回归模型可以精度较高地预测基坑沉降，在已知数据拟合中精度较高，最大拟合误差仅为0.806 mm；在后续4个月的8期预测中，最大残差为1.056 mm，总体均方根误差为0.569 7 mm，满足基坑形变预测的要求。未来若能在基坑数据收集中，搜集更多有关环境数据，例如：温度、湿度等环境因素影响的变化数据，可以更好地参与到支持向量机的预测中，为地铁基坑形变监测提供帮助。