遥感影像K-最近邻图目标分类改进算法的研究

王振力，滕 藤，王 群，黄忠演

（1. 江苏警官学院，江苏 南京 210031；2. 国防科技大学国际关系学院，江苏 南京 210039）

传统的目标检测识别方法[1]如极大似然法、最小距离法和K-均值聚类法等，已经实现利用光谱统计特征完成目标识别与分类，但是当遥感影像中出现大量细节、地物光谱特征较为复杂时，这些传统方法的准确度会降低[2]。针对此类问题，文献[3]提出将机器学习算法应用于高分辨率影像的分类，比如神经网络（NN）、支持向量机（SVM），并且在分类过程中加入影像的纹理、结构等特征。文献[3]方法在提高分类准确率的同时，仍需要进一步提高对目标的具体判别。

文献[4]中提出一种基于K-最近邻图的改进策略，在小样本的情况下可取得较好的结果，但是对于样本数据分布不均匀、待测样本数量较多时效果不佳。针对这一问题，本文提出基于K-最近邻图KNN 改进算法的深度学习模型，以提高对典型目标的分类和判别能力，实现高精度的目标检测[5]。

1 K-最近邻图分类方法的改进

深度学习领域中，可以用于分类的方法有决策树、遗传算法、神经网络、朴素贝叶斯、支持向量机、基于投票的方法、Rocchio 分类、KNN 分类、最大熵等[5]，其中KNN 作为一种较为成熟的算法，是向量空间模型（VSM）下最好的分类算法之一，如图1 所示。

KNN 分类方法是一种传统的无参量、有效、较流行的惰性学习方法，其基本的计算方法如下：记指示器函数为I(x)，有

式中，D 为训练集；x 为待分类的数据对象，本文中表示维度为N 的矩阵；U 为未标记数据集，有x∈U；NK(x,D)为训练集D 中距离x 最近的K 个点，K 称为最近邻阈值；y 为训练集的分类数；

对于待分类的数据对象x，在训练集D 下采用K N N 分类法进行分类，其分类数为c 可能性p(y=c|x,D,K)为

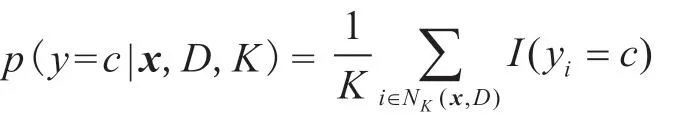
选取最大的p(y=c|x,D,K)值，并将x 标记为分类数为c 的分类，重复此操作直至所有未标记训练集U 中的对象分类完成。

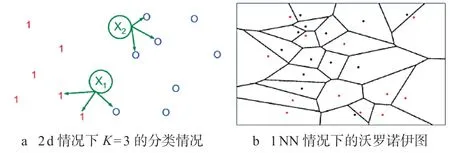
图1 KNN 分类原理示意图

2 基于K-最近邻图的改进策略

2.1 算法的基本思路

文献[4]通过对于K-最近邻图的划分，将必属于某一分类的未标记数据集中的部分数据对象进行分类标号，并加入原训练集，减少噪声数据对于分类的影响。接下来，再对剩余未分类的未标记数据进行KNN 分类。

构造合并数据集D，其中D 包含了训练集U 和样本集R。指定样本集中U 的每一个数据对象xi（i=1、2、…、n）为顶点i，A[i,j]表示从顶点i 到顶点j 的弧。选取每一个数据对象xi最近的k 个数据对象，连接k 条弧。由此，构成了有n 个顶点的稀疏有向图。

根据弧划分该稀疏有向图可知两顶点间的弧数小于（等于）2。

顶点可分为以下三类：

1）顶点i 作为弧头的弧数较多，可以判断该顶点为这一类数据的中心数据对象；

2）顶点i 作为弧头的弧数较少，可以判断该顶点为这一类数据的边缘数据对象；

3）顶点i 不作为弧头，可以判断该顶点为这一类数据的孤立点。

由此不难发现，当两顶点间弧数为2 时，这两个顶点为边缘数据对象。据此，若顶点i 和顶点j 之间的弧数不为2，删去两顶点之间的弧。由此，该稀疏有向图被划分为互不相连的有向子图，n 个数据被划分为多个簇。

根据子图的特点，先给部分未标记数据集中的数据标记并加入样本集。

标记方法如下：

1）在一个簇中，若只存在已标记对象，则不进行处理；

2）只存在未标记对象，则做上标记并等待下一步处理；

3）同时存在已标记和未标记的对象，将所有未标记的对象标记为该簇中出现数量最多的分类，并将该簇中非此分类的已标记对象认作噪声数据，并加以标记。

使用KNN 分类法对未标记的数据对象进行分类。

2.2 算法的改进

将部分未标记数据集中的数据标记时，待测样本的密度直接影响了判断的精度。如果待测样本位于高密度区域，边缘的少数已标记数据会直接决定样本的分类。因此，本文提出在分类时设定一个权值λ=λ0。

显然有0≤λ≤1。

当λ≥λ0时，分类并加入样本集；

当λ＜λ0时，不再将该样本分类并加入样本集，而是留作下一步处理。

该算法中，将未分类样本集的部分样本补充到训练样本中，提高了分类准确率。然而，容易受到已分类和未分类样本偏斜的影响，使得结果向密度更高的类别倾斜，导致误分率增加。为解决这一问题，本文提出针对在第二次分类前进行均匀化裁剪的方法。

记ni为Xi在样本集中ε 邻域中的点的个数，若ni＞MinPts，则称Xi为高密度点。

遍历新样本集的每一个Xi，若Xi为高密度点，在该元素的ε 邻域中的所有点中，删去高密度可达的点，直至该元素没有高密度可达的点或者成为平均密度的点。

ε 邻域的大小为

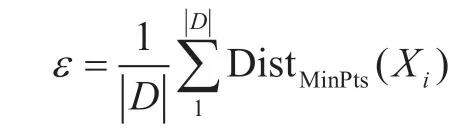
式中，D 为新样本集；Distk 为Xi到距离最近的第k 个样本的距离；MinPts 为最小样本数。根据文献[3]所述，MinPts 选取类别的平均样本数的5%～8%效果较好。

2.3 算法描述

A=[n×n];//n 为数据集的数据对象数

Foreach(Xi in D)

{ S=find_nearest(Xi,k)//找到Xi 的k 个最//近邻

Foreach(Xj in S)

{ A(i,j)=dist(Xi,Xj);//计算Xi 到其k 个最近邻的距离并赋值给邻接矩阵

}

//划分有向图，留下两个顶点间有两条弧的//边缘点

For(i=1;i ≤n;i++)

For(j=1;j ≤n;j++)

If(A(i,j)==0) A(j,i)=0;

//下面利用邻接矩阵A 进行分类，并将分类的//结果加入训练样本

For(i=1;i ≤n;i++)

If(Xi.label==0)S=find_group(Xi);//如果Xi 属于未分类//样本集，则查找Xi 所在簇中的顶点

Foreach(Xj in S)

If(Xi.label==0) num_zero++;

If(Xi.label!=0) num_var++;

//分别计算未分类和已分类的数目

If(num_var/num_var+num_zero＜λ0)

Xi.label=-1;

// 如果λ取值过小，即该簇中的未分类样本比// 重过大，则label=-1

Else Xi.label=mode(S);

//下面对新构成的样本集进行均匀化操作

If(Xi.label!=-1)

X_new=Xi;//X_new 为新样本集

Foreach(Xi in X_new)

While num_neigh(Xi)＞MinPts

//当Xi 为高密度点时

{

Y=pts_neigh(Xi);//找到Xi 的ε邻域的点

l=argmax(|num_neigh(Y(l))|);

Xi=[];//删去ε邻域中密度最高的点

}

//以下使用传统KNN 分类方法来分类未标记对//象

Foreach(Xi in D and Xi.label==-1)

{

S=find_nearest(Xi,k);

Xi.label=mode(S);//用新的样本集对剩//余未分类样本进行分类

}

3 实验结果与分析

仿真实验采用以常见高分辨率卫星影像中飞机目标长宽为基础的模拟数据，选取目标为F-16、F-15、Mig-29 和Su-27 四类飞机。在样本数量上，贴近实际目标出现的频率，模拟了有偏斜的样本[7]和无偏斜的样本，实验中分别运行原方法（文献[4]方法）和改进后的方法。第一组验证样本偏斜对原方法产生的影响，第二组验证改进后的方法对偏斜样本的适应能力。

从图2 可以看出，样本偏斜时，原方法的误分率会显著提高，而整体误分率随着K值的增加呈下降趋势。这是因为在原方法中，样本偏斜较大时，分类的结果倾向于密度较大的类别。

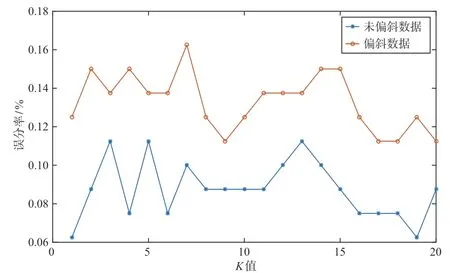
图2 样本偏斜对原方法的影响

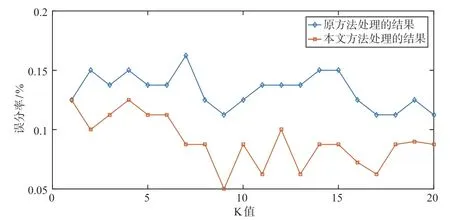
图3 改进方法和原方法在处理偏斜数据时的对比

图3 结果表明对于偏斜数据的处理，改进的方法误分率低于原方法。在K值较低时，样本集的裁剪和权值λ发挥作用不明显，因此误分率的降低不够明显。当K值在10 ～17 时，两种方法的误分率都有一定的降低，但是改进后的方法降低更加明显。当K值超过17 时，误分率又有一定的上升，这是由于样本的数目随着均匀化的裁剪有所降低，使得误分率略有上升。

4 结 语

针对文献[4]方法在偏斜数据上的不足，本文研究了基于K-最近邻图的改进策略，误分率低于该方法。对于权值λ的取值，在本文实验中取0.7 ～0.9 效果最佳，但是如何找到一个通用的方法求出权值λ也是今后研究的方向。