大型商用飞机撞击钢板混凝土结构安全壳的有限元分析

朱秀云，林 皋，路 雨，潘 蓉

(1.大连理工大学 建设工程学部，辽宁 大连 116024；2.生态环境部 核与辐射安全中心，北京 100082)

9.11事件以后，核电厂在大型商用飞机撞击下的安全问题成为关注的焦点。美国于2009年颁布了联邦法规的新条款10CFR50.150[1]，对于新设计的核动力堆均要求就抵御大型商用飞机恶意撞击进行专门评价。为支持10CFR50.150的实施，美国核管会制定了相关的导则RG1.217[2]。目前，我国的核安全法规HAF102[3]针对核电厂抗商用飞机的恶意撞击提出了相关要求，指出如果核动力厂所处的地形条件使其可能遭受商用飞机的恶意撞击，则设计上应考虑这种撞击的影响。技术文件NEI07-13[4]提供了美国电力研究院发展的一套评价大型商用飞机撞击的方法，此套方法是满足联邦法规10CFR50.150并被美国核管会认可的评价方法。对于构筑物整体破坏的评估，NEI07-13推荐了两种分析方法：荷载时程分析法和飞射物-靶体相互作用分析法。目前国内三代核电厂抵御大型商用飞机撞击评估，两种方法均有采用。其中，荷载时程分析法直接用冲击荷载时程函数进行构筑物的响应分析，不需建立飞机的三维有限元模型。

关于核电厂抗大型商用飞机的撞击，近几年来国内外学者进行了较多研究。其中，Lee等[5]建立了大型商用飞机波音747的三维有限元模型，基于飞射物-靶体相互作用分析法进行了此飞机模型撞击预应力混凝土结构安全壳的非线性动力分析；Frano等[6]基于荷载时程分析法对钢筋混凝土结构反应堆厂房进行了一系列波音707、波音747及F4军用飞机的撞击响应初步评估；Sadique等[7]基于荷载时程分析法进行了波音707-320、波音747-400、波音767-400、空客320及F4军用飞机撞击钢筋混凝土结构安全壳的冲击响应对比分析；Iqbal等[8]基于荷载时程分析法进行了波音707-320、空客320及F4军用飞机撞击钢筋混凝土结构安全壳不同位置的冲击破坏对比分析。Thai等[9]针对韩国典型的核电厂屏蔽厂房进行了飞机撞击分析，从整体结构的安全性、局部结构的安全性及撞击诱导振动安全性分析研究了3种不同撞击位置对核电结构的影响。Hua等[10]从多方面阐述了飞机撞击核电厂安全壳的研究进展，并对以往学者的数值模拟和实验研究做出了详细的总结。梅润雨等[11]和李建波等[12]开展了具有隔震构造的核电厂安全壳与飞机撞击的耦合动力响应模拟分析，并对安全壳的振动响应规律进行了评价。梁振斌等[13]和冯尧等[14]分别针对高温气冷堆舱室和乏燃料厂房进行了大型商用飞机撞击过程的非线性有限元模拟，并探讨了结构撞击损伤的影响。上述学者在关于飞机撞击核电厂结构的研究中，对核电厂结构边界条件的处理是将结构底部均视为固定端，而忽视了场地的作用，即假设地基材料为无限刚硬。而在实际工程的动力学分析中，对于非硬基岩场地，往往需要考虑半无限地基的辐射阻尼及场地介质的弹性恢复性能。不同场地的软硬程度对飞机撞击核电厂结构的冲击响应的影响分析很少有文献涉及。

为研究不同场地条件对商用飞机撞击核电厂结构的冲击响应影响，本文采用《核电厂抗震设计规范》(GB50267-97)[15]和美国ASCE4-98[16]推荐的单一弹簧-阻尼器并联系统表征的常系数集总参数模型考虑不同场地的辐射阻尼和弹性恢复性能。以某三维钢板混凝土结构安全壳为研究对象，运用非线性有限元动力分析软件ANSYS/LS-DYNA[17]建立场地弹簧-阻尼器单元耦合安全壳的整体有限元模型，基于荷载时程分析法进行某大型商用飞机撞击安全壳结构的冲击响应对比分析。

1 撞击荷载时程函数

对于荷载时程分析法，首先需确定飞机撞击荷载时程函数。本文撞击荷载选用某大型商用飞机的荷载时程曲线[18]，如图1所示。根据商用飞机的特征，其撞击作用可分为机身和机翼两部分，作用面积均为50 m2，其对应的荷载时程曲线如图2所示，由此撞击作用荷载除以撞击面积，可得到分别作用于安全壳的机身和机翼部分的均布荷载时程曲线，如图3所示。

图1 撞击荷载时程曲线Fig.1 Impact force time-history function curve

图2 机身和机翼的撞击荷载时程曲线Fig.2 Impact force time-history curve of fuselage and wing

图3 机身和机翼的均布荷载时程曲线Fig.3 Impact pressure time-history function curve of fuselage and wing

2 半无限域地基动力数值模型

2.1 规范推荐的集总参数场地动力模型

GB50267-97[15]和ASCE4-98[16]均推荐了集总参数场地动力模型，以6个独立的单一弹簧-阻尼器的并联体系来模拟场地在平动、摆动及扭转方向上的力与变形关系。由于安全壳的圆形筏板基础离散为实体单元，每个节点只有3个平动自由度，只需计算3个平动自由度的地基动刚度。

水平方向的等效弹簧刚度和等效阻尼系数为：

竖直方向的等效弹簧刚度和等效阻尼系数为：

式中：Kx与Kz分别为水平x向、竖直z向的集总弹簧刚度；Cx与Cz分别为水平x向、竖直z向的集总阻尼系数；R为基础半径；ρ为地基材料的密度；ν为动泊松比；G为动剪切模量。由于对称性，Ky=Kx，Cy=Cx。

2.2 地基动刚度的等效离散模型

由于筏板基础厚度较大，假定筏板基础是刚性的。由于平动的土弹簧-阻尼系数并不引起弯矩效应，3个平动方向的弹簧刚度可按照筏板底部单元节点的控制面积进行比例离散。假设集总的平动弹簧刚度为Kx、Ky、Kz，筏板底部节点总数为n，第i个节点所代表的筏板面积为Ai，筏板总面积A=∑Ai(i=1,…,n)，则第i个节点所分配的平动方向的弹簧刚度分别为：

集总的阻尼系数也可近似按照同样的方法进行等效离散，即：

2.3 半无限域地基材料参数

假设了4类均质场地，场地Ⅰ、Ⅱ、Ⅲ、Ⅳ的材料动参数列于表1。场地集总的水平向与竖直向平动的地基弹簧-阻尼系数列于表2。

表1 不同均质场地的材料动参数Table 1 Dynamic material parameter of different homogenous sites

表2 不同均质场地的集总地基弹簧与阻尼参数Table 2 Lumped soil spring and damping parameters of different homogeneous sites

3 数值分析模型

研究对象是某钢板混凝土结构安全壳，该安全壳由外径为51.2 m的圆柱筒体和顶部球冠形穹顶组成，总高度为67.2 m，圆柱筒体和穹顶的墙厚度为1.0 m；安全壳的内、外层钢板厚度均为20 mm。

由于安全壳结构、边界条件和撞击荷载的对称性，分析中采用足尺1/2对称数值模型。混凝土单元类型为Solid164，钢板单元类型为Shell163；钢板与混凝土之间通过共用节点的方式约束，忽略两者间的滑移。其中，混凝土共划分102 018个实体单元、钢板共划分48 720个壳单元；沿墙体以及穹顶厚度方向，混凝土共划分4层单元，即单元的厚度为0.25 m，24 m以下墙体单元的平面网格尺寸为0.6 m×0.67 m，24 m以上墙体单元的平面网格尺寸为0.3 m×0.67 m。

关于安全壳筏板基础的边界条件，针对场地Ⅰ～Ⅳ，均采用无质量弹簧-阻尼单元COMBI165模拟半无限场地。COMBI165单元的一端节点与筏板基础底部节点共用，另一端节点固定端约束，共生成1 769个COMBI165离散单元。由2.2节计算的筏板基础底部每个节点处的离散单元的弹簧刚度与阻尼系数，通过对COMBI165离散单元赋予材料属性来实现，其对应的关键字分别为*MAT_SPRING_ELASTIC与*MAT_DAMPER_VISCOUS[17]。COMBI165离散单元耦合钢板混凝土结构安全壳的有限元模型如图4所示。由于采用1/2对称数值模型，故机身、机翼部位撞击区域的作用面积均为25 m2。作用于安全壳筒身部位撞击区域的单元分布如图5所示，单元的网格尺寸为0.3 m×0.67 m，如图3所示的机身和机翼部位的均布荷载直接施加于此区域钢板单元的正表面。

图4 钢板混凝土结构安全壳有限元模型Fig.4 Finite element model of steel-plate concrete containment

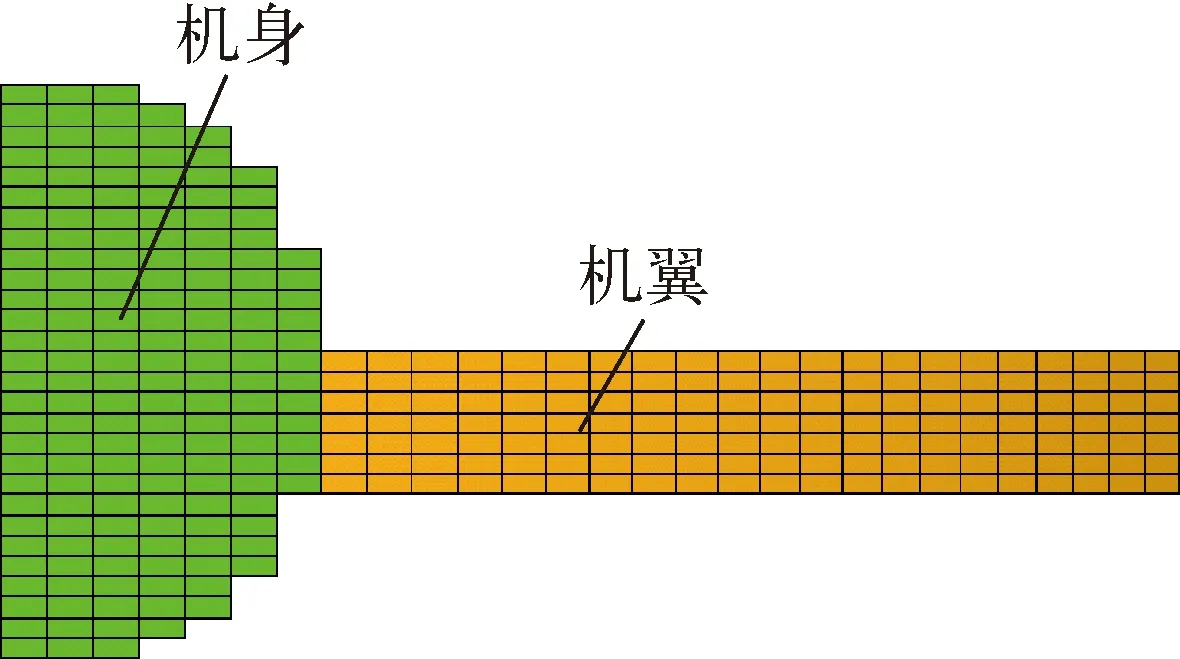
图5 机身和机翼撞击区域的钢板单元Fig.5 Element of steel-plate for fuselage and wing crash zone

钢板选用分段线性动力硬化本构模型(*MAT_PLASTIC_KINEMATIC[17])，混凝土选用模型参数较少且应用方便的WINFRITH本构模型(*MAT_WINFRITH_CONCRETE[17])。在高速碰撞过程中，钢板和混凝土强度会随着材料的高应变率有所提高，本研究采用NEI07-13[4]中推荐的动力强化系数以考虑此特性。考虑动力强化系数后钢板混凝土结构安全壳的基本材料参数列于表3。

基于荷载时程分析法进行飞机撞击的瞬时响应分析，关键是正确描述混凝土、钢板材料的非线性本构关系和失效准则。关于混凝土与钢板材料的本构模型、失效准则及荷载时程分析方法的合理性验证工作主要基于1/7.5缩尺飞机模型垂直撞击不同厚度钢板混凝土墙的实验研究[19]开展的。文献[20]将数值分析方法的验证过程及结论已进行了说明，此文不再进行赘述。

表3 钢板混凝土结构安全壳的材料参数Table 3 Material parameter of steel-plate concrete containment

4 撞击安全壳的数值结果对比分析

在不同均质场地条件下，安全壳筒身最不利撞击部位(距离地面高度32 m中心位置处)[20]受到如图3所示的冲击荷载作用，进行钢板混凝土结构安全壳冲击响应的对比分析。

4.1 不同场地条件的冲击响应对比分析

通过计算，在4种均质场地及安全壳筏板基础底部节点为固定端条件下，撞击区域处节点沿冲击方向的最大位移时程曲线对比如图6所示。图6中场地Ⅰ、Ⅱ、Ⅲ、Ⅳ及固定端的最大位移幅值分别为12.91、12.03、11.69、11.44和10.99 cm。可见，随场地剪切波速增大，其位移响应减小，当考虑为固定端时，其响应最小。撞击过程的安全壳总内能、弹簧-阻尼能及系统总能量的时程曲线对比分别示于图7。可见，不论系统总内能、弹簧-阻尼能还是系统总能量，场地Ⅰ均是最大的，随剪切波速的增大而减小，当为固定端时，其值最小；与场地Ⅰ的安全壳破坏程度最大，固定端时安全壳的破坏程度最小相对应。由此可得：当场地的剪切波速较大，即场地较硬时(如场地Ⅳ)，其冲击响应与固定端相近，假设为固定端的边界条件是合理的；当场地的剪切波速较小，即场地较软时，不论是位移响应还是系统能量曲线均与固定端的结果差异较大。

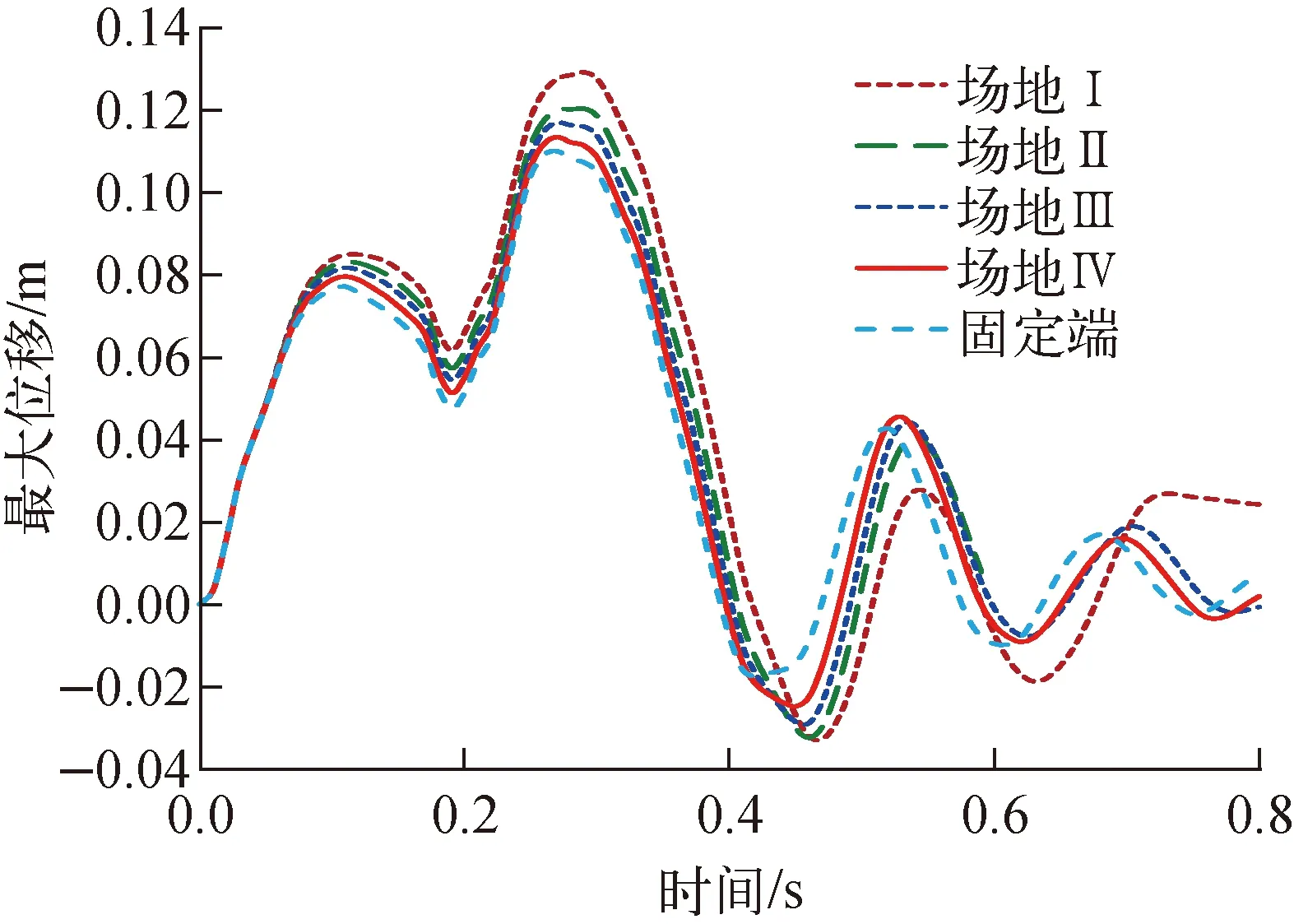
图6 不同场地条件下安全壳最大位移的时程曲线Fig.6 Max displacement curve of containment for different sites

图7 不同场地条件下安全壳总内能、弹簧-阻尼能和系统总能量的时程曲线Fig.7 Total internal energy curve of containment, spring-damper energy curve and total energy curve of system for different sites

4.2 钢板混凝土结构安全壳的冲击响应分析

对于场地Ⅲ，在筒身最不利撞击部位受到如图3所示的冲击荷载作用下，计算得到的安全壳冲击响应最大位移云图及混凝土的最大塑性应变云图，如图8所示。由图8可见：在撞击区域中心位置，其位移响应是最大的，其值为11.69 cm；撞击区域的部分混凝土进入了塑性区，最大塑性应变为9.357×10-4，其他区域混凝土的最大塑性应变为0。

图8 安全壳结构的最大位移(a)和最大塑性应变(b)云图Fig.8 Contour plot of max displacement (a) and max plastic strain (b) of containment

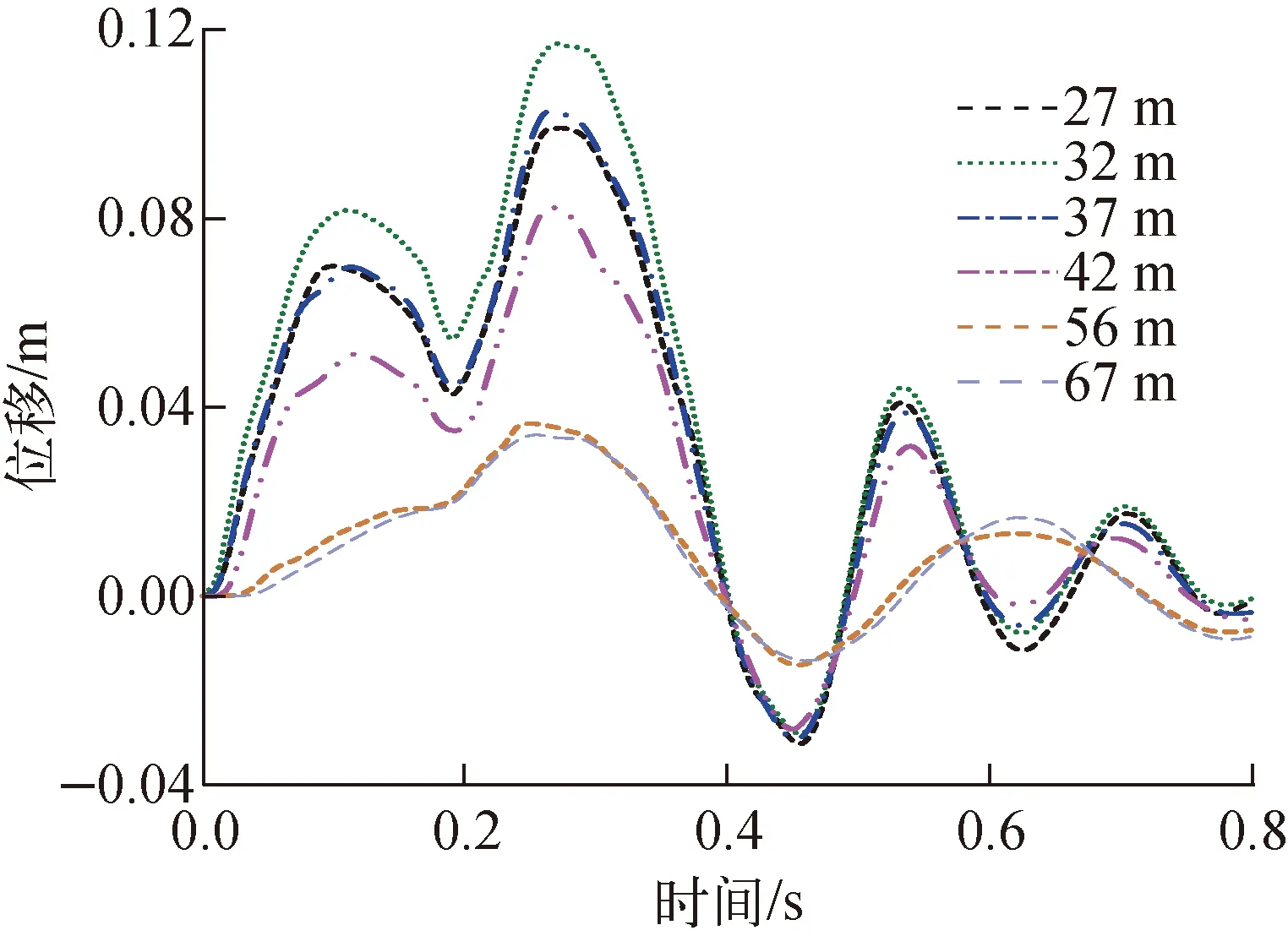
图9 竖直方向不同位置处的结构响应位移时程曲线Fig.9 Displacement curve of different vertical positions

距筏板基础底部不同高度(27、32、37、42、56和67 m)筒体中心处节点沿冲击方向的位移响应时程曲线如图9所示。其中，56 m和67 m处节点分别代表环梁部位及穹顶的顶点。由图9可见，撞击部位节点的位移响应最大，往上不同标高处的位移响应逐渐减小，穹顶顶点处最小。沿机翼撞击区域的水平方向，选取7个不同节点的位置如图10所示，其沿冲击方向(y向)的位移响应时程曲线如图11所示。由图11可见，H1节点的位移响应最大，远离H1节点的位置，直至H7节点的位移响应逐渐减小。综上可知，在大型商用飞机撞击下，钢板混凝土结构安全壳的响应较小，不会引起整体破坏，其整体稳定性是可接受的。

图10 机身和机翼撞击区域水平方向选点位置Fig.10 Horizontal node position of fuselage and wing

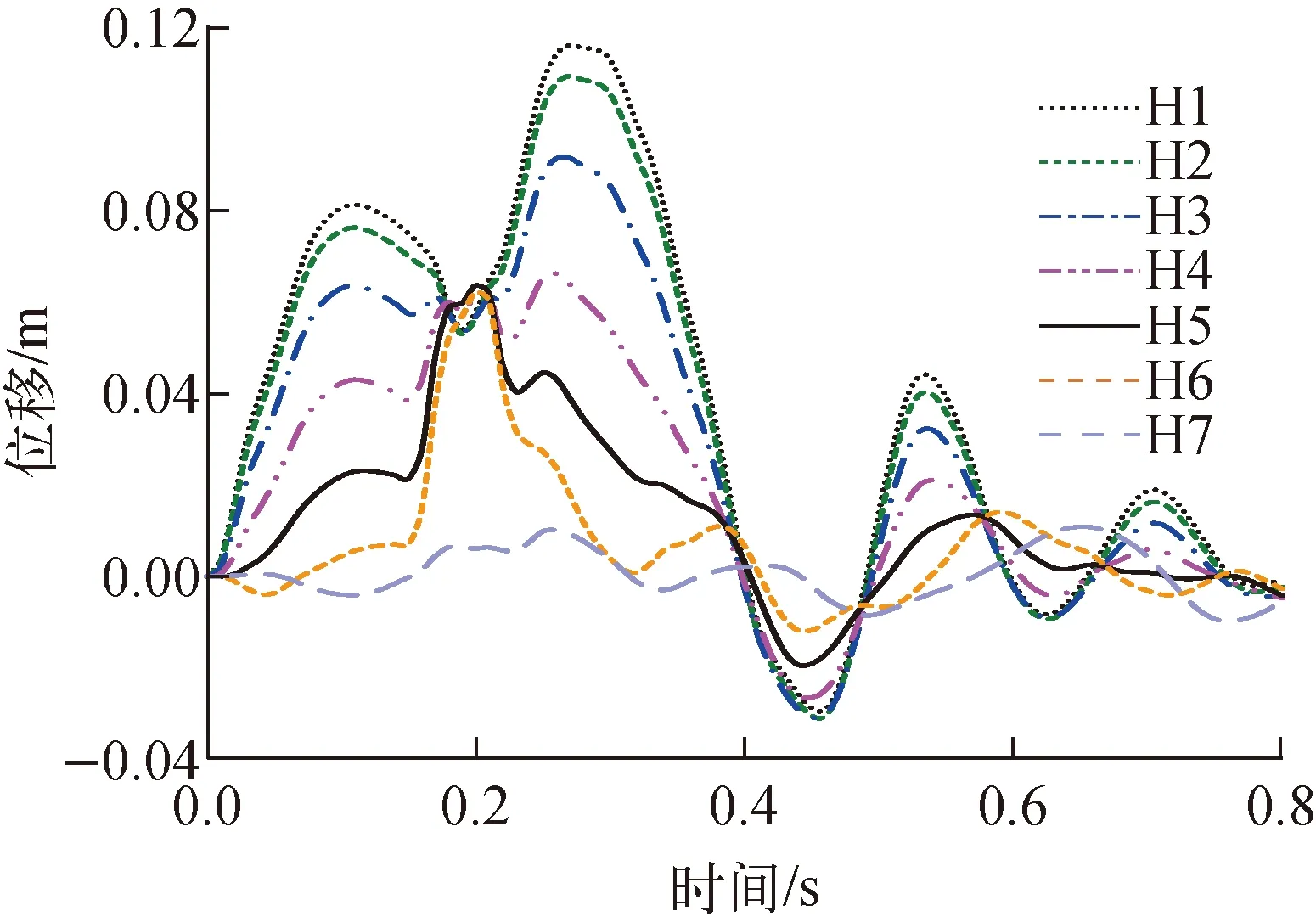
图11 水平方向不同位置处的结构响应位移时程曲线Fig.11 Displacement curve of different horizontal positions

4.3 场地阻尼对于冲击响应的影响分析

在场地Ⅲ条件下讨论场地阻尼对安全壳冲击响应的影响。在撞击区域处节点沿冲击方向的最大位移时程及混凝土的最大塑性应变时程曲线对比示于图12、13。图12、13中：Spring表示忽略场地阻尼，只考虑场地的弹簧效应；Springdamper表示考虑场地的弹簧和阻尼效应；Fixed表示指不考虑场地效应，筏基底部固定端约束。由图12、13可见：由Spring与Springdamper计算的安全壳最大位移时程曲线几乎重合；由Spring与Springdamper计算的最大塑性应变时程曲线很接近，其最大塑性应变分别为9.507×10-4、9.357×10-4，场地阻尼效应对安全壳的最大位移响应及混凝土的最大塑性应变的影响很小。撞击过程的安全壳总内能、弹簧-阻尼能的时程曲线对比示于图14，系统总能量时程曲线对比示于图15。从

图12 安全壳最大位移时程曲线Fig.12 Max displacement curve of containment

图13 混凝土最大塑性应变时程曲线Fig.13 Max plastic strain curve of concrete

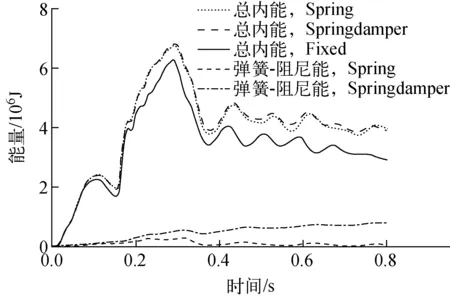
图14 安全壳的总内能及弹簧-阻尼能时程曲线 Fig.14 Total internal energy of containment curve and spring-damper energy curve

图14可见：由Spring与Springdamper计算的安全壳总内能是相当的，均大于不考虑场地效应，即固定端约束的计算值；只考虑场地的弹簧效应时，其自身能量比同时考虑弹簧-阻尼效应的能量偏小。从图15可见：Spring与Springdamper计算的系统总能量曲线基本重合，两者相当，均大于不考虑场地效应，即固定端约束的计算值。由上可见，场地阻尼效应对于冲击响应的影响很小，可忽略不计。

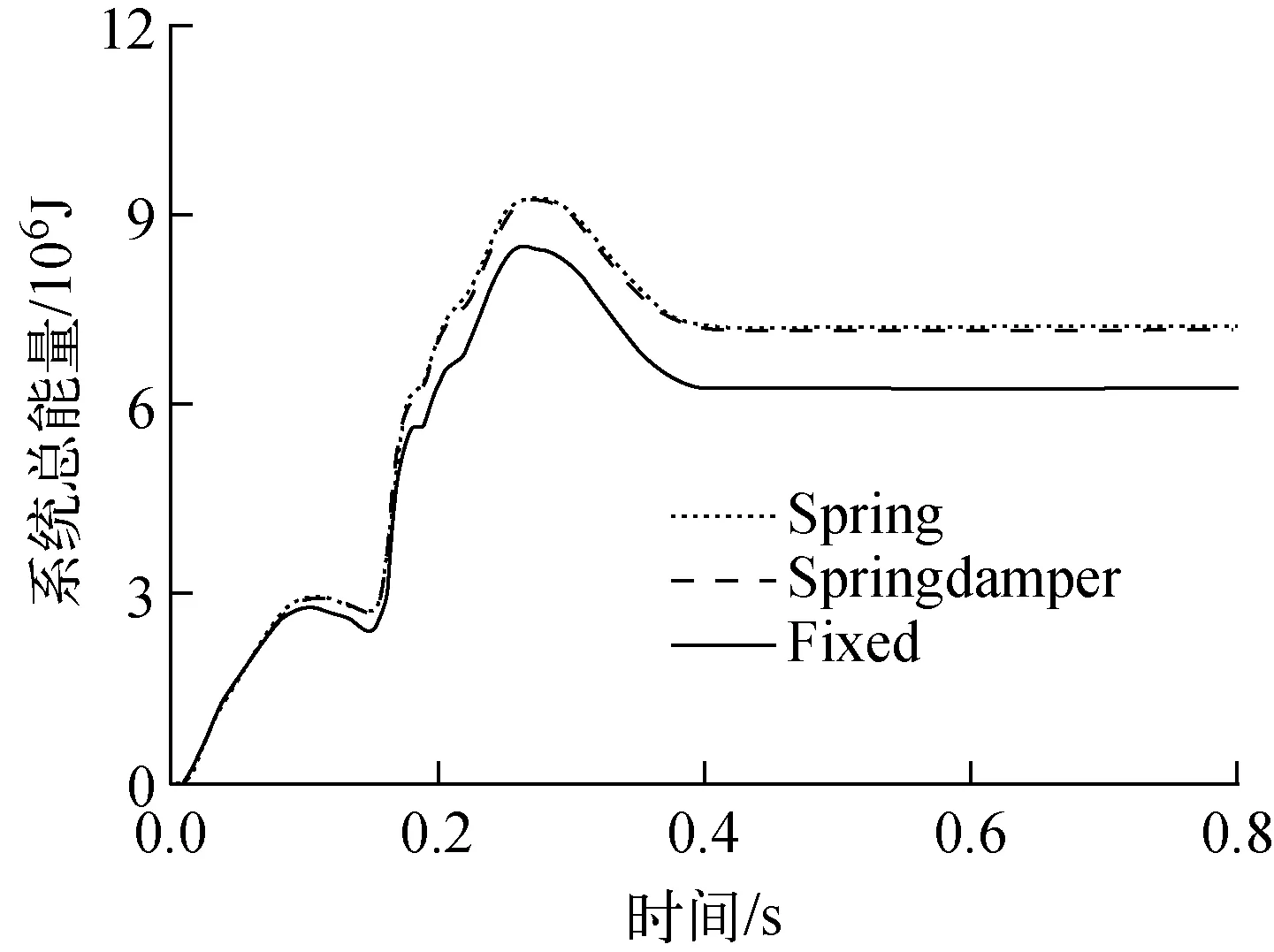
图15 系统总能量时程曲线Fig.15 Total energy curve of system

5 结论

在不同均质场地条件下，基于规范推荐的集总参数场地动力模型考虑场地土的弹性支承和阻尼效应，进行了某大型商用飞机撞击钢板混凝土结构安全壳的冲击响应对比分析，得出结论如下。

1) 随场地剪切波速增大，安全壳的响应减小，当考虑为固定端时，其响应最小。当场地的剪切波速较大(如场地Ⅳ)，即场地较硬时，其冲击响应与固定端相近，假设为固定端的边界条件是合理的；当场地较软时，应考虑场地的弹性作用。

2) 场地的阻尼效应对于冲击响应的影响很小，可忽略不计。

3) 通过对场地Ⅲ条件下安全壳的大型商用飞机撞击分析，可得安全壳结构的响应较小，最大位移为11.69 cm，且只有撞击区域的部分混凝土进入了塑性区，因此不会引起结构的整体破坏，是可接受的。