安全壳外挂水箱结构强度分析
汪孝凡,曹学武
(上海交通大学 机械与动力工程学院,上海 200240)
我国自主设计的第3代核电站大量应用非能动系统,提高了核电站的安全性。其中,非能动安全壳热量导出系统(PCS)依靠自然循环,带走安全壳内热量进而确保安全壳完整性,对核电厂安全运行至关重要[1]。外挂水箱作为PCS的重要组成部分,其完整性尤为关键。但由于外挂水箱的体积和质量相对较大,特别是在地震和温度载荷作用下,外挂水箱内水体的自由液面产生振荡,水体温度升高,可能会对水箱结构的完整性造成破坏,导致PCS丧失功能[2]。
近年来,国内外学者对美国第3代先进压水堆(AP1000)核电站PCS水箱结构和水体的晃动特性进行了大量分析,现有研究普遍采用有限元软件建立安全壳(或水箱)和水体模型,开展时程或反应谱分析。Li等[3]通过将实验与模拟计算进行比对,认为流固耦合计算方法可用于模拟流固耦合作用下核岛建筑物的地震响应。Song等[4]开展了PCS水箱抗震分析,结果表明不能简单认为水箱中的流固耦合作用具有减震耗能的功效,需在水箱结构设计中对该作用加以分析。Zhao等[5]分析了水箱和屏蔽厂房的最大压力分布、最大主应力分布和振荡频率,认为自由液面的晃动对水箱结构的地震响应有较大影响。因此,针对安全壳外挂水箱这一新型结构,有必要对其开展极限安全地震动与温度异常工况组合作用下的结构强度分析。
本文拟建立外层安全壳及外挂水箱有限元模型,采用流固耦合计算方法对外挂水箱进行强度分析,研究外挂水箱在不同载荷下的结构响应及水体振荡特性,为核电厂安全壳外挂水箱安全设计提供参考。
1 分析方法
在外挂水箱强度分析中,水体与结构的相互作用将影响水箱结构以及水体的振荡特性[6],针对该现象,研究者采用多种方法模拟水箱内的流固耦合作用。
Housner[7]提出将刚性储液容器简化为质量弹性系统,如图1所示,将系统压力分为脉冲压力和对流压力两部分。脉冲压力与容器壁的冲击运动产生的惯性力相关,与容器壁的加速度呈正比;而对流压力由流体振荡产生,是脉冲压力作用的结果[8]。然而采用附加质量法计算储液容器的地震动响应时,简化了流固耦合计算问题,忽略了水体振荡对水箱结构的影响[9]。Zhao等[5]及孟剑等[10]开展了流固耦合计算方法分析,认为通过附加质量法计算得到的水箱壁内力偏于保守,未考虑水体振荡,不适用于水箱结构强度分析。
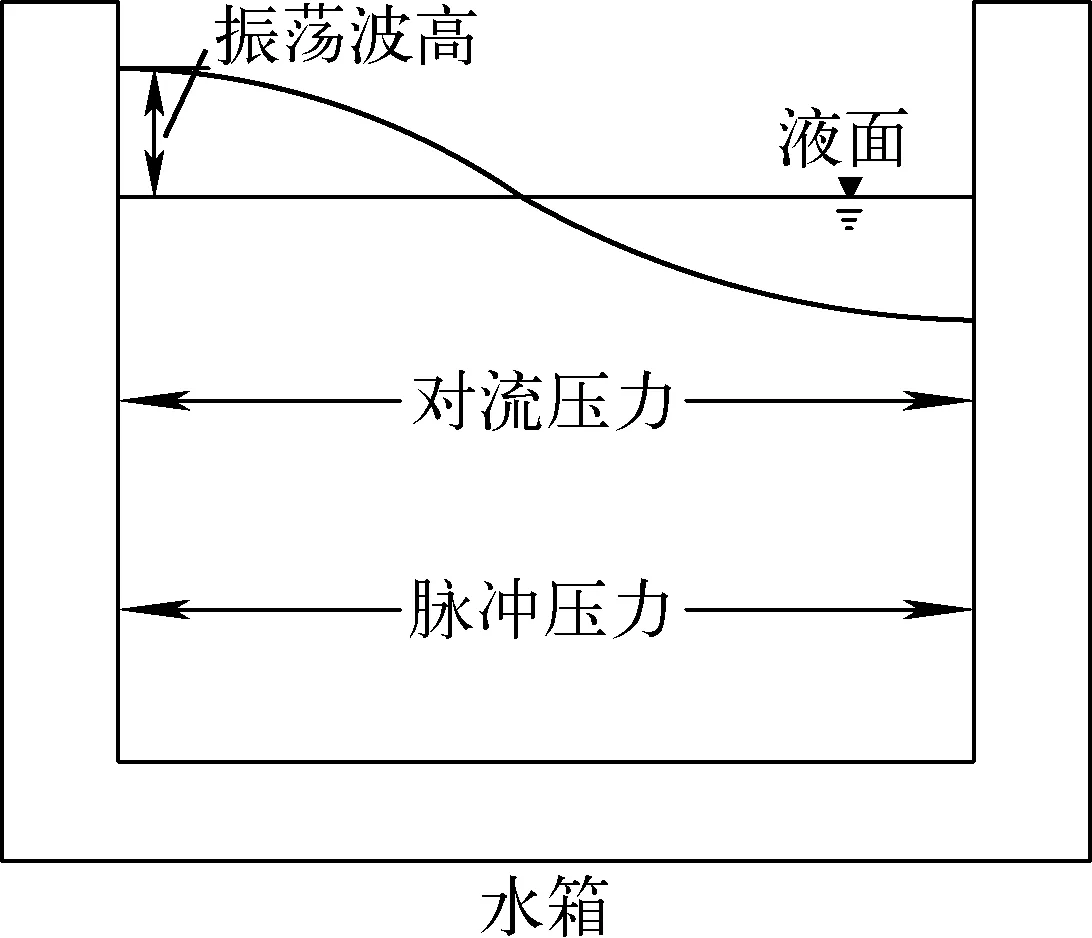
图1 Housner附加质量模型[7]Fig.1 Housner additional mass model[7]
针对此问题,本文采用ANSYS耦合计算方法开展分析计算。ANSYS可通过System Coupling模块实现FLUENT与Mechanical的双向耦合计算。采用Mechanical模拟外挂水箱结构,FLUENT模拟水箱中水体及其自由液面的振荡,并将两者耦合计算,此方法能很好地模拟流固耦合作用[11]。
采用VOF(volume of fluid)模型模拟水箱内气液两相,控制方程包括质量方程和动量方程,如式(1)~(4)所示。
(1)
(2)
ρ=awρw+(1-aw)ρa
(3)
μ=awμw+(1-aw)μa
(4)
式中:v为速度;p为压强;i为分量下标,i=1,2,3,即xi={x,y,z},vi={u,v,w},j为求和下标;ρ和μ分别为混合流体的密度及动力黏度;aw为液相的体积分数;ρw和ρa分别为液相和气相的密度;μw和μa分别为液相和气相的动力黏度。
耦合计算方法中的求解方式属于分离解法,求解过程中引入了流固耦合交界面上的系数,求解方程如式(5)所示。求解计算中在流固耦合交界面进行数据传递,计算模型如图2所示。
(5)
式中:下标F代表流体域,S代表固体域,1代表流固耦合交界面;A为系数矩阵;ΔU为流场中的速度改变量;Δp为流场中的压力改变量;Δδ为水箱位移改变量;R为残差。
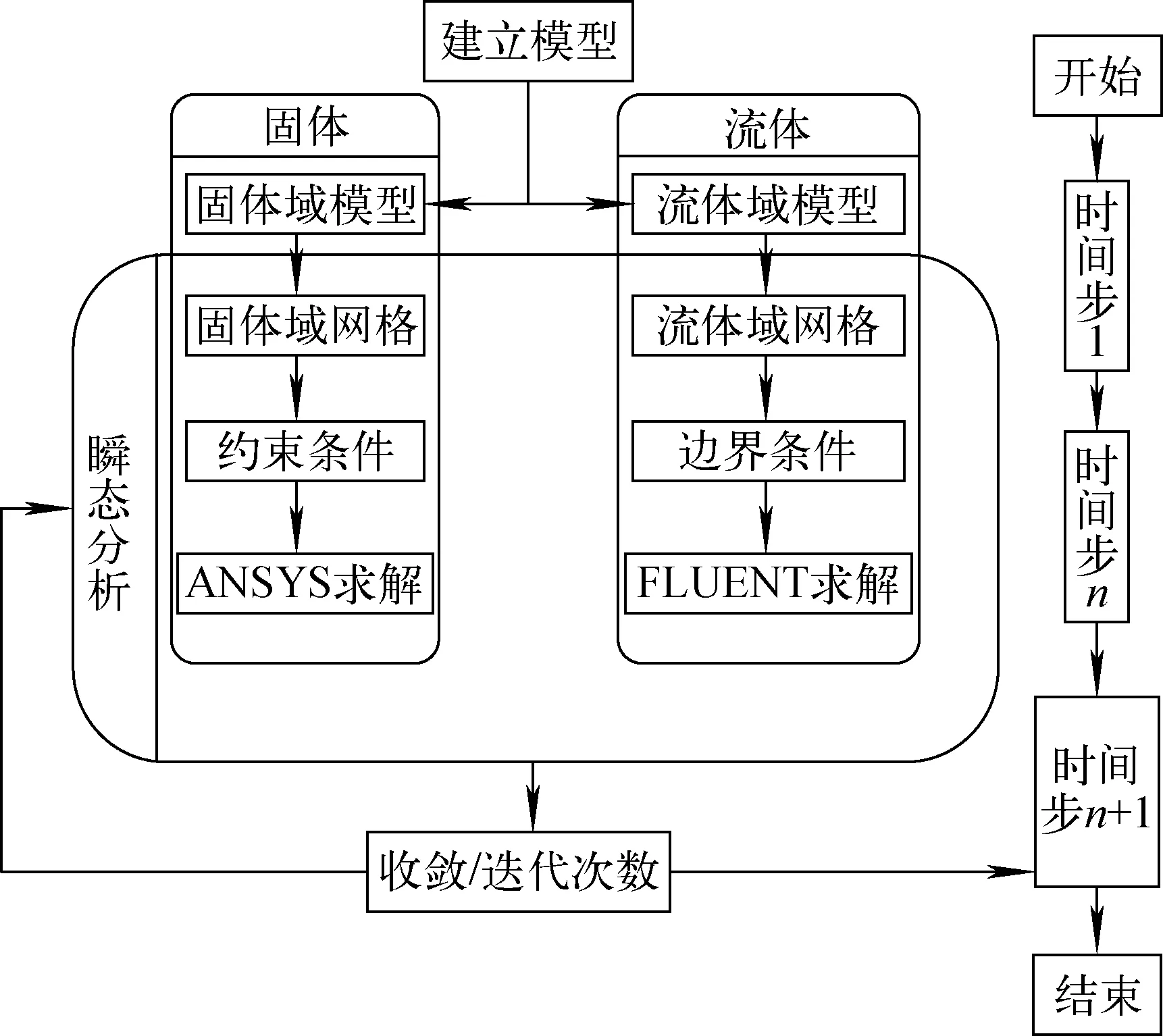
图2 流固耦合计算模型Fig.2 Fluid-structure interaction calculation model
2 模型建立及分析
2.1 计算模型与材料参数
本文建立了整体外层安全壳弥散式钢筋混凝土模型,如图3所示,包括外层安全壳筒体、穹顶、外挂水箱、水箱内流体、燃料厂房和电气厂房。在外挂水箱内建立主要设备简化模型以及贯穿管道模型,包括大型储水罐和换热器,在外层安全壳筒体上建立设备闸门、人员闸门及应急闸门开口,在辅助厂房建立抗大飞机撞击防护门模型。图4为外挂水箱有限元模型,分别为水箱结构部分和流体部分,混凝土结构材料参数列于表1,水的物性参数列于表2。
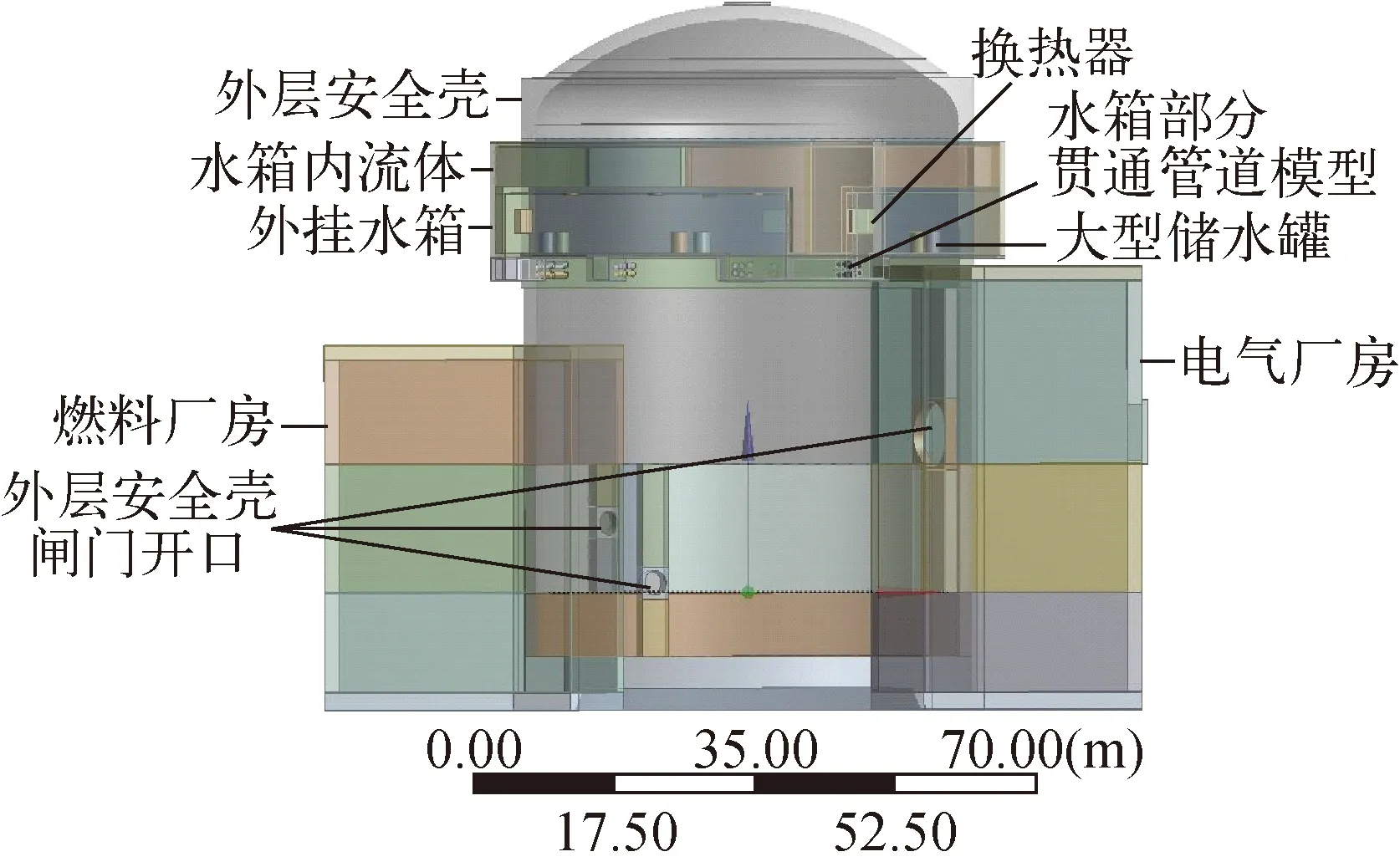
图3 外层安全壳模型Fig.3 Model of outer containment

图4 外挂水箱有限元模型Fig.4 Finite element model of external water tank

表1 混凝土材料参数Table 1 Material parameter of concrete

表2 水的物性参数Table 2 Physical property of water
2.2 网格敏感性分析
对外层安全壳整体模型分步划分网格,包括外层安全壳筒体及穹顶、外挂水箱、水箱内水体和辅助厂房4个部分,开展流体域和固体域网格敏感性分析,网格方案列于表3。考虑到本文侧重于结构强度分析,故通过对比不同网格密度下的结构应力值,确定网格划分方案。根据网格敏感性分析结果,粗糙网格与中等网格应力计算值相差较大,中等网格与精细网格应力计算值非常接近。综合考虑计算精度与计算效率,采用中等网格作为外挂水箱强度分析的网格方案。
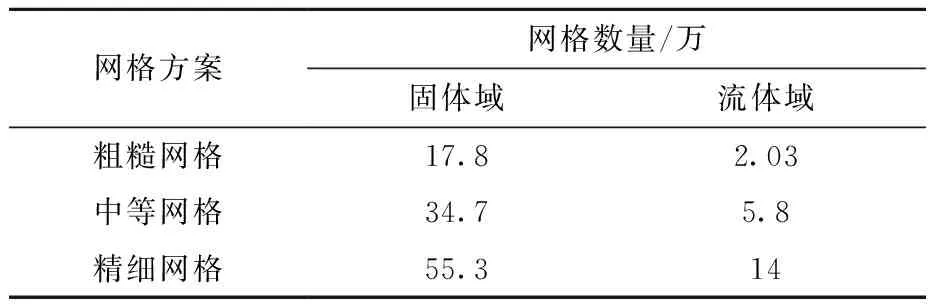
表3 网格敏感性分析方案Table 3 Scheme of grid sensitivity analysis
2.3 模态分析
对外层安全壳有限元模型开展模态分析,研究结构固有频率、模态振型等振动特性。采用完全的直接积分法,对外挂水箱结构开展瞬态动力学分析,系统的阻尼效应采用Rayleigh阻尼[12],即:
C=αM+βK
(6)
(7)
式中:C为系统的阻尼矩阵;M为质量矩阵;K为刚度矩阵;α、β分别为Rayleigh质量阻尼系数和刚度阻尼系数;ξi为结构阻尼比;ωi为结构角频率。
计算结果表明,结构前60阶振型在3个方向上的参与质量比之和均超过了90%,能充分反映结构振动特性[12]。表4列出了结构前10阶频率。选取结构的1阶和2阶自振频率计算,对于钢筋混凝土结构,阻尼比取7%,计算得到α=0.287、β=0.017。

表4 外层安全壳结构前10阶频率Table 4 First ten order frequencies of outer containment building
3 结构强度与水体振荡特性分析
3.1 边界条件与失效判断准则
本文所选取的极限条件为极限安全地震动与温度异常工况组合效应。根据《核电厂抗震设计规范》[13],采用时程分析法对外挂水箱进行抗震分析,选取的3向地震动分别为EL Centro地震动、人工合成地震动以及长周期地震动,以0.3g的地震加速度峰值标定,地震动持续时间为20 s,3向地震动时程的水平分量(x,y方向)和竖直分量(z方向)如图5~7所示。异常工况下安全壳内温度上升,热量传递到外挂水箱内的水体,水温升高并作用于壁面,根据相关研究[14],事故下水箱内壁面温度载荷为110 ℃。

图5 EL Centro地震动Fig.5 EL Centro earthquake
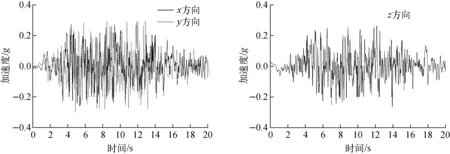
图6 人工合成地震动Fig.6 Synthetic earthquake

图7 长周期地震动Fig.7 Long period earthquake
开展极限载荷下外挂水箱结构强度分析,研究外挂水箱结构的完整性,在强度分析中采用结构应变失效判断准则。根据相关法规要求[13],C60混凝土许用最大拉应变为1.18×10-4,许用最大压应变绝对值为0.001 77。
3.2 EL Centro地震动载荷结构强度分析
对外层安全壳结构同时施加温度载荷和EL Centro地震载荷作用,水箱结构拉应变和压应变曲线如图8所示。外挂水箱结构拉应变在2.6 s时达到最大值9.047 3×10-5,小于许用最大拉应变1.18×10-4;压应变绝对值在2.6 s时达到最大值1.899×10-4,小于许用最大压应变绝对值0.001 77。平均拉应变为6.95×10-5,平均压应变绝对值为1.42×10-4。根据应变曲线得到,外挂水箱结构在地震动加载前期拉应变和压应变较大,这是因为EL Centro地震动前期振动剧烈而后期趋于平缓,最大拉应变和压应变时间点与地震时程峰值时间点吻合。图9为2.6 s时水箱结构最大拉应变和压应变分布,图中应变绝对值最大值表示最大应变位于水箱结构壁面位置,而其他位置应变较小。

图8 EL Centro地震动下外挂水箱结构最大拉应变和压应变曲线Fig.8 Maximum tensile and compression strain curves of external water tank structure under load of EL Centro earthquake
3.3 人工合成地震动载荷结构强度分析
人工合成地震动时程根据设计反应谱生成,是具有代表性的人工合成波[16]。对外层安全壳结构同时施加温度载荷和人工合成地震动时程载荷作用,水箱结构拉应变和压应变曲线如图10所示,外挂水箱结构拉应变在4.8 s时达到最大值1.17×10-4,压应变绝对值在17.2 s时达到最大值2.31×10-4,平均拉应变值为7.82×10-5,平均压应变绝对值为1.93×10-4,均小于许用极限值。外挂水箱持续发生剧烈振动,且结构与地震动的剧烈振动时间一致。外挂水箱结构在4.8 s时的应变分布如图11所示,由于地震动载荷作用和水箱内大型储水罐设备,最大拉应变位于水箱下部结构壁面位置。
相比于EL Centro地震动,人工合成地震动剧烈振动的持续时间更长、幅值更大,水箱结构最大应变与平均应变较大,对外挂水箱结构影响更为严重。根据计算结果及混凝土结构特性,需着重关注结构是否因拉应变过大而导致开裂失效。
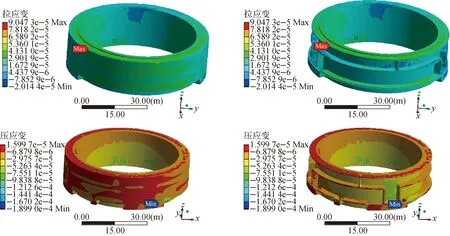
图9 EL Centro地震动下2.6 s时外挂水箱结构拉应变和压应变分布Fig.9 Tensile and compression strain distribution of external water tank structure under load of EL Centro earthquake at 2.6 s

图10 人工合成地震动下外挂水箱结构最大拉应变和压应变曲线Fig.10 Maximum tensile and compression strain curves of external water tank structureunder load of synthetic earthquake

图11 人工合成地震动下4.8 s时外挂水箱结构拉应变分布Fig.11 Tensile strain distribution of external water tank structure under load of synthetic earthquake at 4.8 s
3.4 长周期地震动载荷结构强度分析
长周期地震动会对自振周期较长的结构造成严重危害,而外挂水箱固有频率较低,有必要开展外挂水箱在长周期地震动载荷下的结构强度分析[17]。根据RG1.60谱[18]及Housnar水箱晃动频率公式(式(8)),并以0.3g的地震加速度峰值标定,得到地震动的频率和幅值,以此构成长周期地震动时程。
(8)
式中:h为水箱液面高度;L为水箱半径;g为重力加速度,9.8 m/s2。
外挂水箱结构最大拉应变和压应变曲线如图12所示,外挂水箱结构拉应变在0.8 s时达到最大值9.55×10-4,压应变绝对值在0.2 s达到最大值1.47×10-4,平均拉应变值为9.27×10-5,平均压应变绝对值为1.41×10-4,均小于许用极限值。由于长周期地震动初期振幅较大,结构应变在地震发生初始时刻达到最大值;地震动振动周期长且振动瞬时变化小,外挂水箱结构应变曲线较为平滑,结构平均应变与最大应变相差较小。外挂水箱结构固有频率较低,长周期地震动下结构平均应变较大,表明长周期地震动对外挂水箱结构具有较大影响。外挂水箱结构在0.8 s时的应变分布如图13所示,长周期地震动载荷下流固耦合作用明显,外挂水箱结构在水体域分布位置处的拉应变较大。由于水箱内大型换热器设备和水体振荡对结构的作用,最大拉应变位于水箱下部结构壁面处。
3.5 水体振荡特性分析
为研究水体与固体结构间的相互作用,开展了载荷下外挂水箱内水体的振荡特性分析。根据水箱结构分析结果及应变峰值时间点,分析EL Centro地震动载荷2.6 s、人工合成地震动载荷4.8 s、长周期地震动载荷0.8 s时水箱内的流场,如图14所示。可看出,不同地震载荷下水体振荡特性类似,水体在水箱凹沉处水面振荡幅度较大。

图12 长周期地震动下外挂水箱结构最大拉和压应变曲线Fig.12 Maximum tensile and compression strain curve of external water tank structure under load of long period earthquake

图13 长周期地震动下0.8 s时外挂水箱结构拉应变分布Fig.13 Tensile strain distribution of external water tank structure under load of long period earthquake at 0.8 s

图14 外挂水箱内流场体积分数分布Fig.14 Volumetric distribution of flow field in external water tank
图15为El Centro地震载荷2.6 s时外挂水箱内流场的静压分布,水箱凹沉处水体静压较大、流速较低,而在其上方水面,静压较低、流速相对较大,体现载荷作用下水体的运动,表明水体在水箱凹沉处水面与水箱结构间作用较为强烈。

图15 EL Centro地震载荷下2.6 s时外挂水箱内流场的静压分布Fig.15 Static pressure distribution of flow field in external water tank under load of EL Centro earthquake at 2.6 s
4 总结
本文采用流固耦合计算方法,基于建立的外层安全壳及外挂水箱有限元模型,开展极限安全地震动与温度异常工况组合作用下外挂水箱的强度分析。分别对外挂水箱在EL Centro地震动、人工合成地震动和长周期地震动工况下的结构响应进行分析,研究不同载荷作用下外挂水箱结构应变特性及水箱内流场振荡特性。
在所分析的工况中,安全壳外挂水箱结构最大压应变和最大拉应变绝对值均小于外挂水箱结构许用应变值。EL Centro地震动前期振动剧烈而后期趋于平缓,外挂水箱结构在地震动加载初期拉应变和压应变绝对值达到最大,且最大拉应变和压应变时间点与地震时程峰值时间点吻合。相比于EL Centro地震动,人工合成地震动剧烈振动的持续时间更长、幅值更大,外挂水箱结构应变更大,对结构影响更为严重,结构与地震动的剧烈振动时间一致。在长周期地震动作用下,外挂水箱结构响应变化较小,且应变在地震动加载初始时刻达到峰值;外挂水箱结构固有频率较低,长周期地震动下结构平均应变较大。水箱内水体的振荡特性分析结果表明,水体在水箱凹沉处水面振荡幅度较大,与水箱结构间作用较为强烈。

