辐射流体力学数值模拟中的隐式蒙特卡罗方法

闫 凯

(1.北京大学 数学科学学院，北京 100084；2.西北核技术研究院，陕西 西安 710024)

辐射流体力学广泛应用于天体物理、惯性约束聚变和武器物理等领域中，这些领域均涉及到高能量密度物理，辐射是主要的能量和动量传输方式之一，由于实验环境一般较极端，数值模拟是重要的研究手段之一。辐射流体力学的数值方法大致可分为确定论方法和随机模拟方法。在确定论方法中，由于辐射强度是时间、空间、角度和频率的函数，在数值计算中一般要对辐射输运方程做一定程度的近似，进而得到不同辐射输运近似模型。按照对频率离散方式的不同，辐射输运近似模型可分为灰体近似、多群近似和多带近似等；按照对角度离散方式的不同，辐射输运近似模型包括矩近似、Sn近似和Pn近似等[1]。矩近似是对辐射输运方程进行角度积分，然后求解相应的矩方程组。目前应用较多的是0阶矩近似(经典扩散近似和限流扩散近似)和1阶矩近似。但矩近似方程组并不封闭，因此需给出封闭条件，而这种封闭条件往往是非物理的[2]。Sn近似将粒子运动方向近似为某些特定的方向，然后在每条方向上分别进行求解，但在高维问题中Sn近似方法受到射线效应的困扰[3]。Pn近似是将辐射强度按照角分布展开为一个基本函数全集，但Pn近似在数值模拟中受到波效应的影响，应用相对狭窄[1]。总体来说，确定论方法计算效率相对较高，但由于对辐射输运方程做了某种程度的近似，因此在复杂辐射环境下其计算结果往往需验证。

随机模拟方法又称为蒙特卡罗方法，是一种基于概率统计的数值模拟方法。在20世纪40年代，蒙特卡罗方法就被应用到数值计算中，但受限于计算机的计算能力，直到1971年Fleck等[4]提出隐式蒙特卡罗(IMC)方法后，蒙特卡罗方法才逐渐大规模地应用到热辐射输运问题中[5-7]。近十几年，辐射流体力学的蒙特卡罗方法发展较迅速，Nayakshin等[8]采用蒙特卡罗方法模拟辐射输运过程，通过统计得到辐射压力，用于光滑粒子流体动力学(SPH)的计算。Harries等[9-11]讨论其开发的辐射输运蒙特卡罗程序TORUS，在后续的工作中，该程序用来模拟辐射流体力学问题[12-14]。Noebauer等[15]给出了一种辐射与物质完全耦合的蒙特卡罗方法，其在辐射输运过程中提出对光子的能量沉积和动量沉积进行统计，该方法能保证守恒性。Roth等[16]首次给出了辐射流体力学的IMC方法，但对IMC方法的实施细节讨论较少。另外，其在蒙特卡罗模拟中统计的物理量为辐射能密度和辐射能流，然后通过一个关于时间的向前欧拉格式来更新流体动量和能量，但这种做法不能保证守恒性。本工作结合Noebauer和Roth数值方法中的优点，采用IMC方法模拟辐射输运问题，在模拟过程中通过统计能量和动量沉积来更新流体能量和动量。

1 辐射流体力学方程组

不考虑黏性和体积力，实验室坐标系下的流体力学方程可写为：

(1)

(2)

(3)

省略相关物理量的空间和时间变量，实验室坐标系下辐射输运方程为：

(4)

其中：Iν为单频辐射强度；n为光子运动方向的单位向量；ni为n在i方向的分量；ην为单频发射率；χν为单频总不透明度。为方便介绍，引入单频辐射能密度Eν、单频辐射能流Fν和单频辐射压力pν，其表达式分别为：

Fν=∮nIνdn

(5)

由于辐射与物质相互作用的复杂性，为方便计算，做如下假设：1) 物质满足局部热力学平衡条件；2) 在流体静止系中散射是弹性碰撞；3) 散射碰撞后的方向在流体静止系下是各向同性的。为区分两种坐标系，用下标0表示流体静止系，若无下标0则表示实验室坐标系下的物理量。流体静止系下不透明度和发射率可表示为：

(6)

(7)

(8)

给出3种常用的平均不透明度系数，分别为平均辐射能密度不透明度χ0E、平均普朗克不透明度χ0P和平均辐射能流不透明度χ0F，其表达式分别为：

(9)

四元组表达式可简化为：

(10)

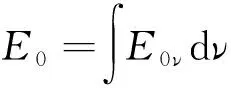
(11)

其中，γ=(1-uiui/c2)-1/2为洛伦兹因子。

2 数值方法

采用算子分裂思想将计算分为3步：第1步计算不含辐射与物质相互作用项的流体力学方程组；第2步计算辐射输运方程，采用IMC方法进行计算；第3步通过统计沉积能量和动量来更新流体能量和动量。流体力学的数值方法已相对成熟，这里主要介绍考虑相对论效应的IMC方法。

2.1 热辐射输运问题的IMC方法

IMC方法最初应用于热辐射输运问题，即只考虑辐射与物质能量的耦合，而不考虑流体的运动过程。以一维灰体为例，不考虑散射情况下，即χ=χt，热辐射输运方程组可表示为：

(12)

(13)

其中：I为辐射强度；μ为光子方向与x轴正方向夹角的余弦；S为独立外源项。

引入平衡辐射能密度ur为：

ur=aT4

(14)

定义β为：

(15)

在每个时间层[tn,tn+1]中用tn时刻的值来近似β、χ和S，即：

β(t)≈βn

χ(t)≈χn

S(t)≈Snt∈[tn,tn + 1]

(16)

则热辐射输运方程为：

(17)

(18)

(19)

其中，α为给定的常数，α∈[0.5,1]。对式(18)关于时间[tn,tn+1]积分，可得到：

(20)

化简后得到：

(21)

定义Fleck因子f为：

(22)

则式(21)可写为：

(23)

t∈[tn,tn+1]

(24)

将式(24)代入到式(17)、(18)可得到：

(25)

(26)

利用内能和平衡辐射能的转化关系，并对能量平衡方程关于时间积分，最终得到内能的时间离散形式为：

(27)

(28)

2.2 辐射流体力学问题中的IMC方法

在辐射流体力学问题中，当流体速度较大时，经典IMC方法不再适用，本文推导了考虑相对论效应的IMC方法。其中时间和空间的离散均在实验室坐标系下进行，粒子的运动也是在实验室坐标系下的时空中，但辐射与物质的相互作用即蒙特卡罗粒子的碰撞事件发生在局部的(每个单元)流体静止系下。通常所说的不透明度均是指其在流体静止系下的值，散射是各向同性的假设也是基于流体静止系的。两种坐标系下光子频率和角度满足的关系为：

(29)

(30)

在流体静止系下，假设满足局部热力学平衡，根据霍尔基夫定律，每个单元(体积为ΔV0)在单位时间(Δt0)内发射的能量ε0为：

ε0=χ0Pcu0rΔV0Δt0≈χ0PcurΔVΔt

(31)

在IMC方法中，吸收系数被有效吸收系数代替，则：

ε0≈fχ0PcurΔVΔt

(32)

假设流体静止系下蒙特卡罗粒子的能量权为w0，其中w0是任意给定的，则该单元上蒙特卡罗粒子的个数Nemit为：

(33)

每个蒙特卡罗粒子代表一束具有相同位置、发射时间和频率的光子，因此粒子的能量权在两种坐标系下的转化关系为：

(34)

两种坐标系下蒙特卡罗粒子的数目是一致的，通过式(29)、(30)可得到蒙特卡罗粒子在实验室坐标系下的角度、频率及能量权。蒙特卡罗粒子的空间位置和发射时间的抽样与经典IMC方法一致。抽样给出热发射源的粒子状态后，需统计实验室坐标系下因热发射而产生的每个单元上的物质能量损失ΔE′m和动量损失Δp′，则：

(35)

(36)

其中，下标i表示单元上的第i个粒子。

在蒙特卡罗粒子的追踪过程中，需抽样给出碰撞距离。对于经典IMC方法，若介质的不透明度为χ0，则粒子飞行的轨迹长度ds为：

(37)

其中，ξ3为0～1之间的随机数。即粒子飞行ds的距离后发生1次碰撞，在实验室坐标系下，介质的不透明度与粒子运动方向相关，两种坐标系下的转化关系为：

χ0ν0=χν

(38)

联合式(29)、(38)可给出实验室坐标系下的不透明度，碰撞距离抽样仍可仿照式(37)，将流体静止系下的不透明度替换为实验室坐标系下的不透明度即可。在追踪粒子的运动过程中，需统计粒子的能量和动量沉积。碰撞一般分为吸收和散射。对于吸收事件，粒子飞行距离ds后，其能量沉积密度ΔEm和动量沉积密度Δp分别为：

(39)

(40)

其中，上标p、f分别表示碰撞前、后的物理量。

(41)

在此过程中，能量沉积密度和动量沉积密度分别为：

(42)

(43)

结合式(35)～(36)和式(39)～(43)，可给出1个时间步总的能量沉积密度ΔEm,tot和动量沉积密度Δptot。更新流体物理量，在此过程中流体的密度保持不变，则：

ρ(un+1-un)=Δptot

(44)

(45)

最后通过状态方程更新流体的温度和压力。

3 数值结果

3.1 辐射平衡问题

测试气体在辐射作用下的加热和冷却过程，在此过程中可验证辐射输运部分蒙特卡罗程序的正确性。本文选择Turner&Stone算例[17]，计算区域气体始终处于静止状态，即不考虑相对论效应的影响，其热容为9×10-7J·cm-3·K。区域内存在一均匀的、各向同性的辐射场，辐射能密度为105J/cm3，对应的辐射温度为3.4×106K。忽略辐射对物质动量的影响，这种情况下流体的能量方程为：

(46)

本文考虑两种情况：1) 气体被辐射加热，取初始时刻的气体温度为11 K；2) 气体冷却过程，取初始时刻气体的温度为1.1×109K。两种情况下辐射能密度均远大于气体能量密度，这意味着能量交换的过程中辐射能密度是近似不变的，因此气体温度最终接近于辐射温度。图1为IMC方法计算结果与解析解结果的比较，其中时间步长为10-15s，蒙特卡罗粒子数取为10 000，可看出，两者结果吻合良好。

图1 IMC方法计算结果与解析解的比较Fig.1 Comparison of IMC calculation and analytic solution results

3.2 稳态辐射波

Lowrie等[18]给出了经典扩散近似下一维辐射流体力学方程组关于稳态波结构的半解析解结果，在其分析中，方程组的稳态解可由4个物理量参数决定：上游气体的马赫数M，光速和上游气体的声速的比率C，上游辐射压力(乘以3)与上游气体压力的比率P0，光学厚度τ。

根据文献[18-19]，取P0=10-4、C=1.732×103、τ=577。初始时刻上游气体处于辐射平衡状态，温度和密度均为1，根据状态方程可知此时的声速为1，上游气体速度取为马赫数，下游气体的状态根据间断跳跃条件计算得到，IMC方法基于式(1)～(4)进行模拟。图2为M=2时物质密度、速度、温度及辐射温度的稳态解，可看出，计算结果与半解析解结果基本一致，初步验证了程序的正确性。

3.3 非稳态辐射波

算例来自文献[20]，文献[15-16，21-22]先后对此算例进行了测试，并对模型进行了简化，本文采用文献[22]中的简化模型。一维计算区域长度为8.7×108m，左边界为反射边界，右边界为自由边界，计算区域内气体为氢原子，其初始温度为50 K，密度为7.78×10-5kg/m3，绝热系数Γ=1.4，不透明度为3.1×10-8m-1，初始时刻气体以-6×103m/s或-2×104m/s的速度向左面运动，两种速度下计算得到的辐射波分别为亚临界辐射波和超临界辐射波。图3分别为亚临界辐射波和超临界辐射波中物质温度和辐射温度的分布[16]，可看出，两者结果基本一致，但在辐射前驱波区域，本文计算结果偏大，这可能是由于辐射输运模型的差异导致的。图4为未考虑和考虑相对论效应IMC方法的计算结果比较，可看出，在早期两者的结果基本一致，但当计算到1.3×104s时，两者结果出现了较为明显的差异，考虑相对论效应的IMC方法物质温度升得更快，尽管物质速度(-2×104m/s)仅约为光速的万分之一，但对计算结果已有明显的影响。

图2 物质密度、速度、温度及辐射温度的稳态解Fig.2 Steady state solution of material density, velocity, temperature and radiation temperature

图3 亚临界(a)和超临界(b)辐射波中物质温度和辐射温度分布Fig.3 Material and radiation temperature distributions under subcritical shock (a) and supercritical shock (b)

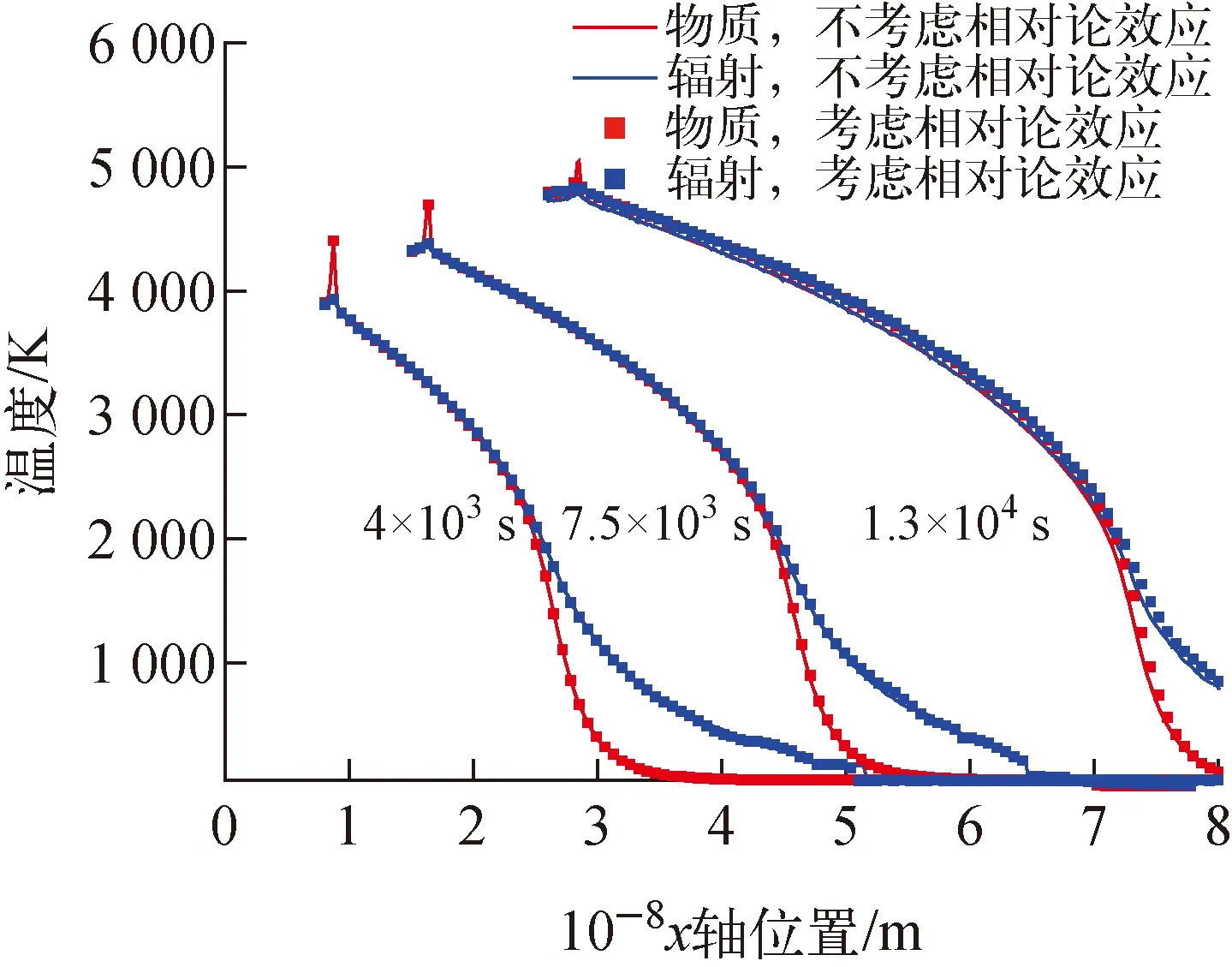
图4 两种IMC方法计算结果的比较Fig.4 Comparison of result by two IMC methods

4 结论

本文研究了辐射流体力学数值模拟中的IMC方法。介绍了在不考虑流体运动过程的IMC方法，给出了该方法在辐射流体力学问题中详细执行过程。与热辐射输运问题相比，IMC方法需考虑辐射流体力学的相对论效应。在模拟过程中给出了粒子的能量和动量沉积的统计方法，这种处理能保证守恒性。最后给出了几个典型问题的数值模拟结果，并与相关的参考解进行对比，对比结果验证了算法和程序的正确性。