基于AgW触点材料的大功率继电器触点间的电动斥力

张 杰

（贵州航天电器股份有限公司，贵州贵阳 550009）

引言

当有电流流过继电器触点时，电流线在接触面附近发生收缩，由于自身磁场与电流的作用，平行于接触面的电流线分量具有电磁力，因而在触点间会出现相互排斥的电动斥力[1]。这是一种电流自身磁场作用下的电动力。它的存在会减小触点的有效接触力，延长触点闭合过程的回跳时间，使触点易于产生熔焊，特别是大功率继电器更是如此。

首先简单介绍了继电器触点材料的一些情况，然后建立继电器触点间电动斥力的研究模型，通过该模型对AgW触点间的电动斥力进行分析研究，得出电动斥力与W含量的关系曲线。

1 触点材料简介

一般地，用作继电器触点的材料[2]有3类，即纯金属材料、合金材料和复合材料。

1.1 纯金属材料

纯金属触点材料常见的有Al、Cu等。Al是较好的导电材料，但由于它不耐弧、在空气中易氧化生成不导电的绝缘薄膜，不是很好的触点材料。Cu的导电与导热性比Al好，硬度、熔点、沸点比Al高，是应用最广泛的导电材料。但它在空气中也易氧化生成不导电的绝缘薄膜，故限制了其作为触点材料的进一步发展。

1.2 合金材料

Ag合金：AgAu合金耐腐蚀，但易硫化；PdAg合金与AgAu合金类似，但其电阻率大、电阻温度系数小。该类合金价格较贵。

Au合金：AuNi合金随Ni含量的增加电阻率增大，有较好的抗熔焊和桥接转移能力，但在电弧作用下易氧化、使接触电阻增大。AuPt合金在温度升高时不易氧化。AuAg Pd合金硬度高，不易氧化，但易于形成桥接转移。该类合金价格很贵。

1.3 复合材料

AgCdO：AgCdO是广泛应用于低压电器的触点材料，它具有以下特性：在电弧的作用下CdO分解，从固态升华到气态，产生剧烈的蒸发，体积会增大好几个数量级，起着吹弧作用，且清洁触点表面。但Cd及CdO蒸气有毒，对人体健康有影响，因而AgCdO触点材料必将会被逐渐淘汰。

AgW：该材料的性能与AgCdO类似。随着W含量的增加，抗电弧磨损和抗熔焊能力增强，但导电性能有所下降。当W含量在50%～80%时材料性能最佳，常用作大电流继电器触点的电接触材料，主要用于重负载且开闭不频繁的场合。

2 触点间电动斥力的理论计算

2.1 模型的建立

为了计算继电器触点间的电动斥力，采用图1所示的接触导体模型。为了便于问题的处理，作以下假设[3]：

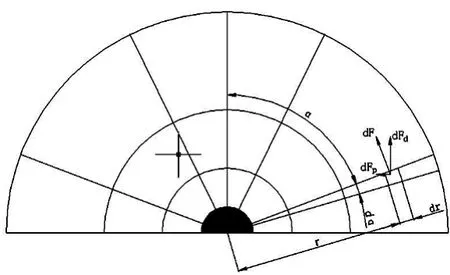
图1 电流-电位场

(a)导体为非磁性材料；

(b)导体周围为空气；

(c)接触面内全部导电斑点集中在中心形成一个大的导电斑点；

(d)该导电斑点是一个超导小球，为一个等位体。

在假定条件下，触点间收缩区中的等位面变成一系列与超导小球同心的圆球面，电流线则为一系列通过超导小球中心的辐射状直线。

2.2 电动斥力的推导

在图1中，dr处导体元dα的磁场强度为：

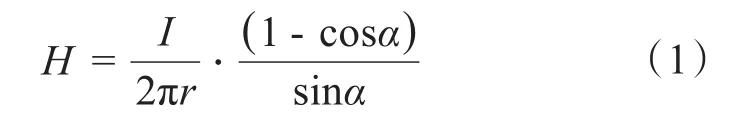
设流过导体元dα的电流为dI，则dr环所受的电动力为：

式中，μ0为空气的磁导率。

将dF分解成平行于视在接触面的分量dFp和垂直于视在接触面的分量dFd。由于电流线为对称分布，平行分量互相抵消，剩下垂直分量，为：

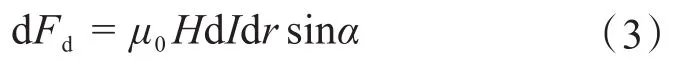
而dI=Isinαdα，故

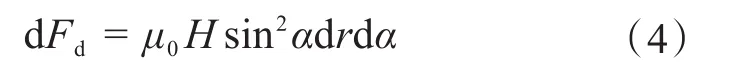
所以，触点间的电动斥力为：

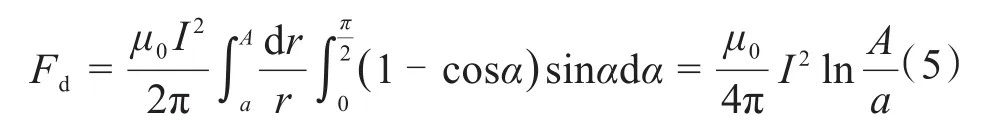
式中，A为导体截面半径，a为接触斑点半径。

式（5）表明，触点间的电动斥力只与触点的最大导电截面和最小导电截面有关，与电流在收缩区内的过渡情况无关。

接触斑点半径由赫兹公式导出：

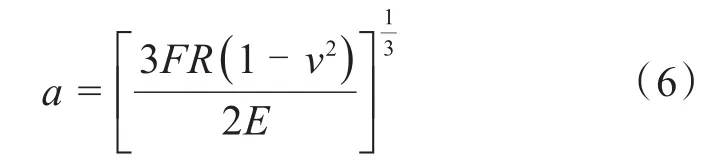
式中，F为触点的接触压力，R为触点的球面半径，E为弹性模量，ν为泊松比。

2.3 AgW触点材料接触斑点半径的处理

本研究讨论的是AgW触点间的电动斥力，故只处理AgW触点材料的接触斑点。在AgW触点材料中，W含量不同，其弹性模量和泊松比也发生变化。在不知道W材料具体含量的情况下，假定它符合混合物规律[5]，即

弹性模量为：

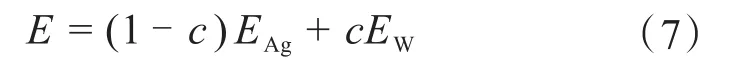
泊松比为：

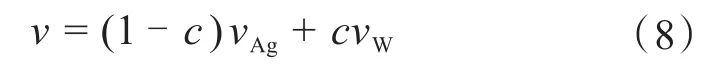
式中，c为W的含量。

2.4 AgW触点间接触力的计算

计算时，采用图2所示典型的大功率继电器触点模型。在该模型中，触点的接触方式采用点接触形式，取触点压力为2.5 N，触点球面半径20 mm，导体截面半径3.5 mm，流过触点的电流为100 A，Ag的弹性模量7.58×1010Pa、泊松比0.39，W的弹性模量34.45×1010Pa、泊松比0.284。将以上值代入式（5），得触点间的电动斥力与W的含量的关系曲线，如图3所示。

图2 典型的触点模型

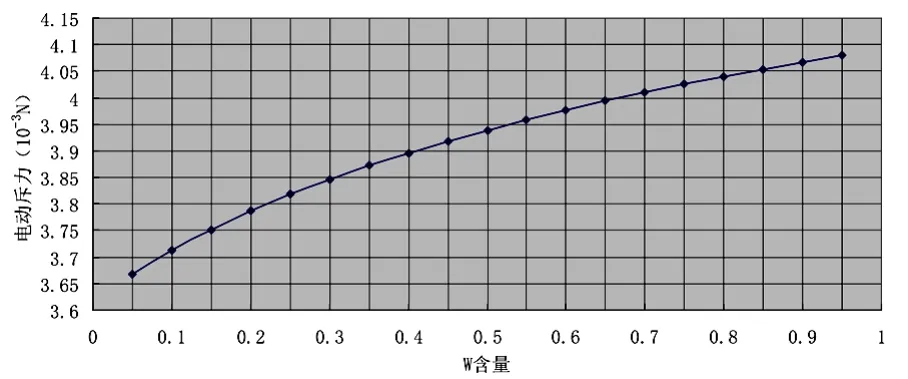
图3 AgW触点间的电动斥力与W含量的关系

由图3看出，随着W含量的增加，AgW触点间的电动斥力变大，但该力只分布在（3.7×10-3～4.1×10-3）N，与大功率继电器触点间的接触压力（2.5 N）相比要小得多，几乎可以忽略不计。

实际上，继电器触点不管是点接触，还是线接触、面接触，其导电斑点往往有多个，故式（5）的使用受到限制。但是，式（5）作为估算触点间电动斥力的上限值，特别是点接触形式下的上限值，仍然是有用的。

在大功率继电器中，有时为了减小触点间的电动斥力，可以采用多触点并联结构，电动斥力由每个触点平均分摊。也可以将触点固定连接在由高弹性材料制成的连接零件上，且使电动斥力的方向与弹性零件由于形变产生弹力的方向相反，从而起到克服电动斥力的作用。

3 结论

（1）对两相或多相机械混合的金属复合材料，在不清楚其具体的物理参数（如弹性模量、泊松比等）的情况下，可以按混合物规律进行求解；

（2）分析计算表明，AgW触点材料随着W含量的增加，AgW触点间的电动斥力变大；

（3）AgW触点间的电动力总的来说不大，与接触压力相比可以忽略不计；

（4）触点间的接触斑点往往不是一个，故计算结果对估算触点间的电动斥力上限值有指导意义；

（5）当需要克服触点间的电动斥力时，可以采用多触点并联结构，或将触点固定连接在由高弹性材料制成的连接零件上。