辐射伏特效应核电池换能器件中的β粒子能量沉积行为

张明旭 秦李鑫 赵 嫚 赵江涛

（兰州大学核科学与技术学院兰州730000）

近年来，在航空航天、深海探索等领域，人们迫切需要比传统化学电池性能更好的替代品，其中放射性同位素电池由于寿命长等优点越来越受到重视。放射性同位素电池［1-3］（核电池）是一种将放射性同位素衰变能转换成电能的新型电池。目前，常见的核电池主要包括温差核电池、辐射伏特效应核电池、光伏核电池这三大类［1］。其中，β辐射伏特效应核电池［4-5］因其具有可微型化、能量密度高、寿命长等特点而成为微机电系统［6］电源的最佳选择。β辐射伏特效应核电池应选择衰变粒子能量适中、半衰期长、并且衰变过程中未伴随X和γ射线发射的纯β放射源。常见的β放射源包括3H、35S、63Ni、147Pm、90Sr。其中90Sr衰变释放的粒子能量过高而易损坏换能单元，35S半衰期仅有87.44 d，不能满足微机电系统对微能源长寿命的需求。因此，3H、63Ni和147Pm是β辐射伏特效应核电池放射源的主要选择［7］。考虑到微型电源的能量密度需求，63Ni是β辐射伏特效应核电池放射源的首选。换能器件一般选择工艺制作成熟且极限转换效率较高的半导体材料［8-14］。综上分析，本论文选择63Ni作为β辐射伏特效应核电池的放射源，同时选择硅（Si）、砷化镓（GaAs）、碳化硅（SiC）、氮化镓（GaN）这4种常用半导体材料作为辐射伏特效应核电池的换能材料。

在对β辐射伏特效应核电池的转化效率进行仿真计算时，β粒子在换能材料中的能量沉积规律是关键，它直接关系到β粒子在换能材料中激发的电子-空穴对的数密度分布。然而，放射源衰变产生的β粒子能谱是连续的，并且会与其自身原子以及换能材料原子的核外电子发生非弹性碰撞，使其电离或激发，从而损失能量。此外，β粒子还会与原子核碰撞发生轫致辐射能量损失。对于63Ni放出的β粒子来说，其平均能量为17.4 keV，主要发生电离能量损失。此外，在这一能量范围，电子的多次散射现象也比较显著［15-16］。因此，连续能谱β粒子在换能材料中能量沉积的计算很复杂，理论上还缺少这方面的研究。所以，只有通过完整的蒙特卡罗模拟计算，才能准确反映连续能量的β粒子在放射源中的自吸收及其在界面的反散射过程，进而精确计算出其在换能材料中的能量沉积分布。近年来，Tang等［17］利用MCNP程序计算了63Ni衰变放出的β粒子在Si、GaN中的自吸收和沉积能量规律。刘玉敏等［18］利用MNCPX计算了63Ni表面出射活度密度和表面出射能谱的平均能量。Belghachi等［19］则通过自主编写的蒙特卡罗程序计算了63Ni在不同换能材料中的反散射和出射功率。刘秋月等［20］利用蒙特卡罗软件Casino软件计算了单能β粒子的反散射情况。然而，Casino软件只能处理单能电子，难以模拟放射源的自吸收过程。作为一款商业软件，MCNP（X）在使用时不仅面临版权限制，而且其计算模型是封装在一起的，使用者难以了解其中的计算细节，因此可扩展性也较差。

综上分析，基于通用的开源蒙特卡罗程序框架开发通用程序，来对放射源产生的连续能量β粒子在换能器中的能量沉积行为进行研究就显得十分重要。Geant4［21-23］是由欧洲核子中心（CERN）开发的一套基于C++的开源蒙特卡罗程序框架，它提供了多种粒子类型及粒子与物质相互作用截面库，可用于精确计算各种粒子在物质中的输运过程，包括电子、光子和电子-光子的耦合输运过程。本文基于Geant4程序框架，建立了模拟β粒子在换能器件中能量沉积过程的通用模型，并通过与Casino的结果进行对比，验证了Geant4在模拟β粒子在换能器件能量沉积规律上的准确性。进而，利用建立的仿真模型计算了63Ni放射源的自吸收、表面出射粒子能谱，β粒子在材料表面的反散射行为以及在几种常见换能材料中的能量沉积规律，为准确模拟β辐射伏特效应核电池的能量转化效率提供了进一步的数据支持。

1 仿真模型设计与验证

1.1 模型设计

在Geant4框架内，建立了仿真计算模型，如图1所示。其中图1（a）为PN结型换能器的计算模型，包括63Ni放射源和换能材料。图1（b）为肖特基型换能器的仿真计算模型，即在放射源和换能材料中间添加了一层肖特基金属层（0.1μm厚的镍膜）。放射源为63Ni体源，厚度可变，β粒子出射方向为4π立体角内各向同性，63Ni的β衰变能谱参考了美国布鲁克海文国家实验室（Brookhaven National Laboratory，BNL）的数据。换能材料分别为硅（Si）、砷化镓（GaAs）、碳化硅（SiC）、氮化镓（GaN），厚度为50μm，横截面均为1 cm×1 cm。

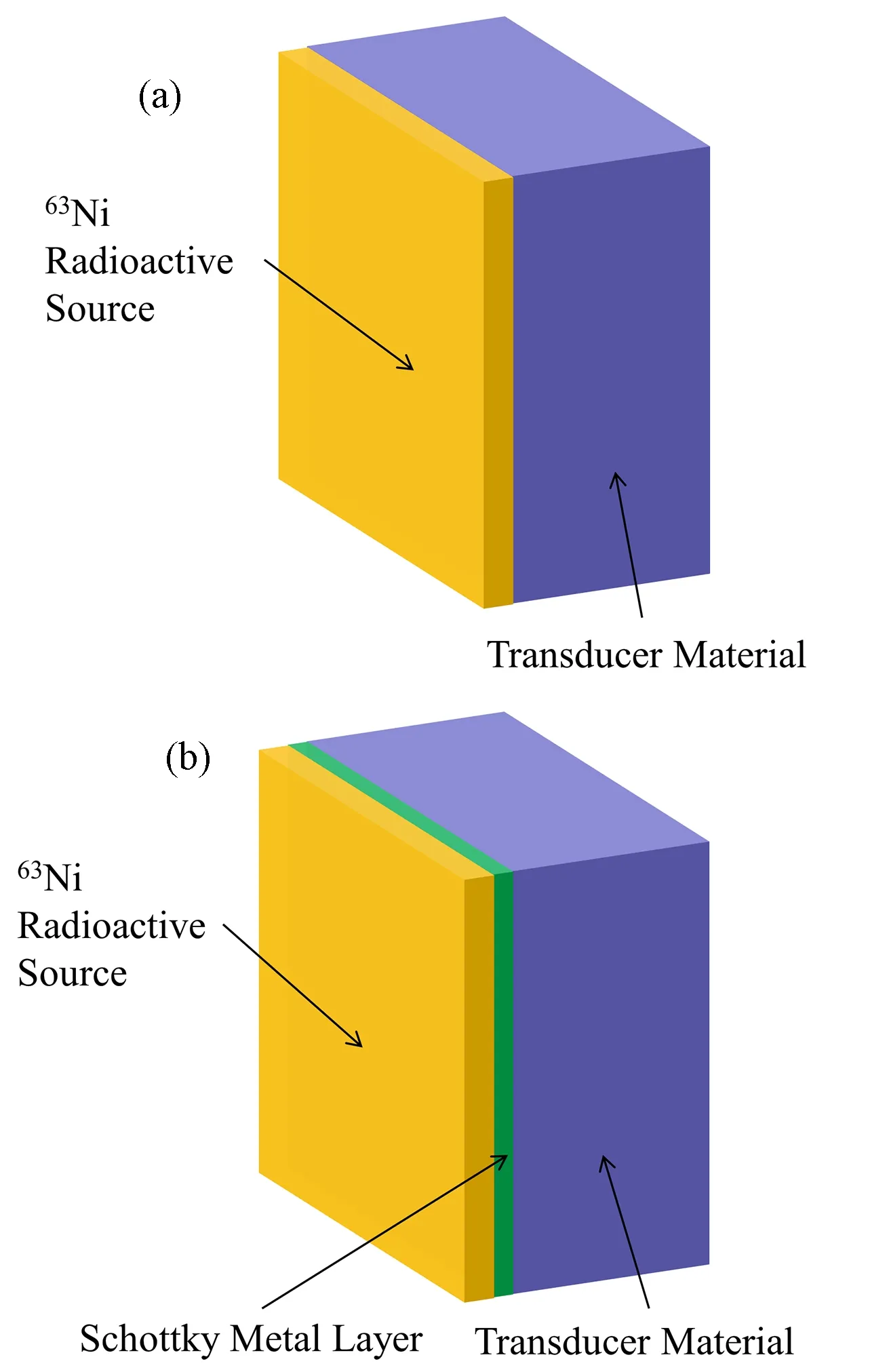
图1 PN结型(a)和肖特基型(b)β辐射伏特效应核电池模型Fig.1 Model of nuclear battery withβradiation effect:(a)PN junction type,(b)Schottky type

在描述63Ni放射源释放的β粒子与物质的作用机制时，Geant4提供了多种电磁物理模型供用户选择，比如：emstandard_opt4、emlowenergy、emstandardWVI等［24］。这三种模型都是基于标准电磁物理过程而开发的，其中emstandard_opt4模型对低能反应过程进行了优化，emlowenergy采用了实验低能反应模型，而emstandardWVI则采用Wentzel VI模型来对全能量段的e-和e+的多次大角度库伦散射以及单次弹性散射进行计算。初步计算发现：emstandard_opt4和emlowenergy模型在计算单能电子（17.4 keV）在硅靶中的透射率时存在缺陷，即随着硅厚度从1μm增加到4μm，前者给出的电子透射率始终约为2%，后者则恒为0，这显然不符合电子在硅中的射程规律。在使用emstandardWVI模拟时，电子透射率随着厚度的增加而减小，在4μm处透射率为0.2%。因此，本文选择emstandardWVI作为描述低能电子-靶物质相互作用的电磁物理模型。

1.2 可行性验证

为了验证Geant4在模拟低能电子-换能材料原子相互作用中的准确性，计算了17.4 keV的单能电子在硅中的能量沉积分布和反散射情况，并与Casino的计算结果进行了对比。其中，硅靶为5μm×5μm×5μm的立方体，粒子源为半径10 nm的圆面源，入射方向与硅靶表面法线方向夹角分别为0°、25°、50°和75°，模拟粒子数目为105。计算结果如图2所示。

图2 结果表明：Geant4模拟17.4 keV单能电子在硅中的能量沉积分布规律和Casino的计算结果基本吻合，在计算反散射率时，Geant4计算结果略高于Casino的计算结果。总体上，可以认为利用Geant4对63Ni的β粒子发射能谱和出射、吸收功率等物理量进行计算是可行的。

图2 单能电子在硅靶中的能量沉积(a)及反散射率(b)Fig.2 Energy deposition(a)and backscattering rate(b)ofsingle-energy electrons in silicon target

2 结果与分析

2.1 63Ni的发射能谱和出射、吸收功率

通常，放射源的自吸收会随着放射源厚度的增加而增加，从而影响表面出射能谱以及出射功率。图3为63Ni放射源表面出射能谱随放射源厚度的变化规律。由图3分析可知，随着放射源厚度的增加，其内部的一些低能β粒子被其自身吸收，高能β粒子由于能量较大，穿出了放射源，导致总的出射粒子数目减少。随着高能β粒子占比越来越大，总的表面出射粒子能谱峰位从低能区向高能区移动。当放射源的厚度饱和时，放射源内部的一些高能β粒子也无法出射，使得其出射能谱基本不再变化。

基于Geant4模拟，图4给出了17.4 keV单能电子在硅靶和镍靶中的反散射率，入射方向与靶表面法线方向夹角分别为0°、15°、30°、45°、60°、75°，其余参数与§1.2所述一致。由图4可知，随着入射角度的增加，电子在硅和镍中的反散射率不断增加，且在镍表面的反散射率明显大于在硅表面的反散射率。在小角度入射情况下，电子在镍表面的反散射率甚至比硅大了50%，这会对能量沉积产生直接的影响。

图3 63Ni放射源在不同厚度下的出射β粒子能谱Fig.3 Energy spectra of emittedβparticles from 63Ni radioactive source with different thicknesses

图4 单能电子在硅靶和镍靶中的反散射率Fig.4 Backscattering rate of single energy electrons in silicon target and nickel target

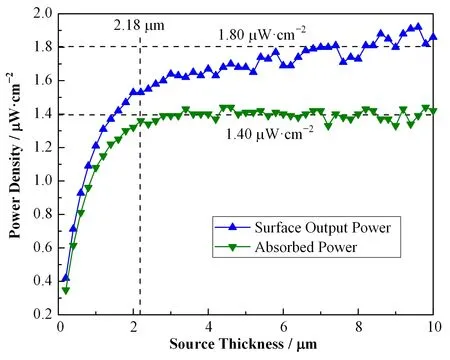
图5 63Ni放射源在不同厚度下的表面出射功率密度和硅（PN结型）中的吸收功率密度Fig.5 Output power density of 63Ni radiation source at different thicknesses and the absorbed power density of silicon(PN type)

图5 给出了63Ni放射源的表面出射功率及在PN结型换能器中的能量沉积功率，图6则给出了其在肖特基型换能器中的模拟结果。由图5可知，随着放射源厚度的增加，表面出射功率也在增加。然而，当放射源的厚度增加到2μm左右时，内部的一些高能β粒子无法出射，使得表面出射功率增加减缓，直至表面出射功率在1.8μW·cm-2上下波动。刘玉敏等［18］利用MNCPX计算得出当63Ni裸源厚度增加到2μm时，其上下表面总出射功率密度接近饱和值，约为3.2μW·cm-2，与本文的结果一致。此外，图5计算结果也表明：换能材料的吸收功率低于放射源的表面出射功率。由图4可知，入射电子在硅中的反散射率随入射角的增大而增大，那么从63Ni源表面的边缘处或者近边缘处发射的大角度入射电子很可能直接穿出换能材料或者在界面处经过库伦散射穿出换能材料，从而使得吸收功率比表面出射功率降低了约0.4μW·cm-2。

从图4还可以看到，电子在镍中的反散射率明显大于在硅中的反散射率，所以由于0.1μm厚的镍金属层的存在，使得β粒子穿过镍层时发生了较强的反散射，进而损失一部分能量，导致硅基底肖特基型换能器件中沉积功率比PN结型换能器件小了约0.3μW·cm-2，如图6所示。

图6 63Ni放射源在不同厚度下的表面出射功率密度和硅（肖特基型）中的吸收功率密度Fig.6 Output power density of 63Ni radiation source at different thicknesses and the absorbed power density of silicon(Schottky type)

综上分析，在使用63Ni作为放射源时，最佳的放射源厚度应保持在2～3μm，在此基础上增加放射源的厚度并不能显著增加输出功率。同时，由于实际吸收功率低于放射源表面出射功率，因此在计算核电池转化效率时应以实际吸收功率为准。

2.2 不同换能材料中的能量沉积规律及其饱和厚度

核电池中电子-空穴对的数目及其分布与核电池的输出性能密切相关。因此，研究放射源在不同换能材料中的能量沉积规律就显得十分重要。定义换能材料的饱和厚度为沉积能量占换能材料总沉积能量90%时的厚度。设置63Ni体源的厚度为2μm，换能材料的厚度为50μm，材料类型包括硅（Si）、砷化镓（GaAs）、碳化硅（SiC）、氮化镓（GaN），其余几何参数保持不变。图7给出了2μm63Ni源在4种换能材料中的能量沉积分布曲线。

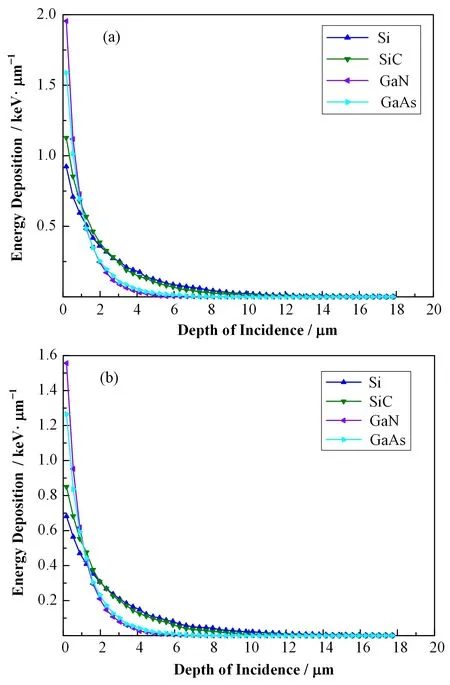
图7 2μm 63Ni源在PN结型(a)、肖特基型(b)换能材料中的能量沉积分布Fig.7 Energy deposition distribution of 2μm 63Ni source in PN junction type(a),Schottky type(b)transducer material

由图7可知，β粒子在GaN和GaAs的能量沉积曲线比较陡峭，而在Si和SiC中的则相对平缓，此外在GaN和GaAs中的能量沉积较Si和SiC的大，在大约1.5μm内β粒子在GaN和GaAs中的能量沉积要比在Si和SiC的能量沉积大30%左右，而β粒子在GaN和GaAs的单位深度能量沉积除了在近表面有些差别之外，其余部分基本保持一致，在2μm左右沉积大部分能量。此外，还可以看到，0.1μm的肖特基金属层使得β粒子在换能材料中的能损值有一定程度的降低。为了得到β粒子在换能材料中的有效能量沉积区域，这里统计了沉积能量占换能材料总沉积能量90%时的厚度，如表1所示。

由表1可知，2μm厚的63Ni放射源在GaN和GaAs中的能量沉积主要集中在3μm以内，而在Si和SiC中的能量沉积主要集中在7μm以内，工程上应用时，换能材料厚度可参考这些数据选取。

表1 不同换能材料的饱和厚度Table 1 Saturated thickness of different transducer materials

3 结语

本文基于Geant4程序框架建立了通用模型，对β粒子在辐射伏特效应核电池换能材料中的能量沉积规律进行了详细研究。通过对比Casino软件在单能电子能量沉积和散射规律上的计算结果，验证了Geant4在模拟放射源产生的β粒子在核电池换能器件能量沉积上的可行性。进而，分析了放射源厚度的增加造成的表面出射功率和发射能谱的变化，并确定了最佳放射源厚度。结果表明：在使用63Ni放射源时，其表面出射粒子能谱的峰位随源厚度的增加而向高能区移动。此外，63Ni放射源的最佳厚度应保持在2.2μm左右，再增加放射源的厚度并不能显著增加输出功率。在最佳厚度的情况下，63Ni放射源在不同换能材料中的能量沉积分布规律并不相同，2μm厚的63Ni放射源发射的β粒子在上述4种换能材料中的能量沉积主要集中在7μm之内，这为核电池的优化设计提供了依据。本工作建立的通用模型也可扩展至任意β放射源和换能材料组合，计算准确且应用不受限制。