辽宁省春季透雨集合预报误差分析

(沈阳中心气象台，辽宁 沈阳 110166)

引言

辽宁省地处于东亚大陆，具有温带大陆季风气候的属性，春季一般干旱少雨，但同时又容易出现大风天气。辽宁省是中国的农业大省，春季干旱是影响粮食产量的重要因素[1-2]。而辽宁春季的降水预报尤其是关于透雨预报是春播的重要服务工作，做好春季透雨预报不仅关系到辽宁的粮食安全，而且是关乎国计民生的大事。由于降水是在一系列复杂物理过程的影响下所形成，受多种天气系统共同影响，所以降水预报相对于气压、风速、气温等天气要素的预报准确率低，成为天气预报和气候预测中最有预报难度的天气要素之一[3]。因此提高降水预报的准确性一直是气象业务与科研工作的重点之一[4]。近年来，集合预报产品对降水预报的准确度有所提高[5]，但由于降水这一天气要素本身和数值模式的不确定性，集合降水预报仍然存在不小的误差。随着现代计算机技术的迅猛发展，集合预报仍是数值天气预报未来发展的方向[6-8]，因此需要对降水集合预报进行检验评估，从而在较多数值预报产品中提取更多有用的预报信息[9]。武英娇等[10]研究了ECMWF 集合降水预报在安徽省大别山区降水分级预报中的应用效果。许敏等[11]对廊坊地区降水预报数值产品的释用能力进行检验发现，各模式对各类别降水准确率各不相同。赛瀚等[12]、张宁娜等[13]对多种数值预报产品在东北地区的降水预报进行检验表明，不同模式对不同要素的预报效果各不相同。由于春季是过渡季节，大尺度环流形势从冬季的大槽大脊型向平直型转换，因此环流形势多槽脊活动，形势演变比较快。通过影响系统来看，移动性的低涡活动逐渐增多，这样容易使数值模式对春季降水预报能力降低。因此，如今的各数值模式对透雨的预报在辽宁特别是辽西干旱的背景下准确率不同，急需对各模式集合预报关于辽宁春季降水模式预报产品的预报效果进行评估，以便得到各模式对其更准确且更有用的信息。

2005年世界气象组织在全世界范围启动了一项为期10 a的THORPEX计划，TIGGE是其中的子项目，它为全球概率天气预报的发展提供了所需要的数据[14]。随着集合预报数量的增加，其包含的预报信息逐渐丰富，通过集合预报数据进行研究并获得成果的同时，还需充分了解集合预报的误差特点[15]。本文从确定性效果检验和概率性效果检验两个方面对2016—2018年辽宁地区春季4—6月CMA、ECMWF和NCEP 3套全球集合预报结果应用多种误差计算方法，分析3套全球集合预报产品在辽宁地区春季降水预报误差特点，以期为辽宁省春季透雨预报提供参考。

1 资料与方法

1.1 资料来源

在日常的气象业务工作中，透雨预报是春季播种期最为重要的农业服务产品之一，研究辽宁省透雨预报误差特点很有意义。春季透雨一般定义为4—6月的春播期第一次出现全省10个站及以上，24 h降水量超过10.0 mm的降水。本文为扩大样本数量，将其在2016—2018年4—6月内全省10个站及以上24 h降水量超过10.0 mm的降水均进行误差检验，样本总数为46个，其中2016年有21个，2017年有10个，2018年有15个。

本文的预报资料来自世界气象组织(World Meteorological Organization，WMO)交互式全球大集合(THORPEX Interactive Grand Global Ensemble，TIGGE)项目。目前，世界气象组织设立了3个TIGGE资料中心，分别为中国气象局(CMA)、欧洲中期天气预报中心(ECMWF)以及美国国家大气研究中心(NCEP)，它们分别作为资料全球交换中心，接受来自全球10个主要预报中心的集合预报产品。使用双线性插值的方法将各中心不同预报时段的集合降水格点预报资料插值到站点上，获得研究区域内站点集合预报资料，观测资料为同时段62个国家级气象站(图1)日降水资料。

1.2 确定性预报检验方法

集合预报的确定性检验，主要检验各集合预报中心以及各集合成员的降水预报与降水实况的偏差。确定性预报检验方法很多，本文主要选取两分类检验评分(如TS评分)作为确定性预报的检验方法。下面是检验方法所用检验量的具体介绍。

TS评分基于两分类常用的评分方法，其作为对降水确定性预报的评分指标已经纳入确定性预报的评分体系中[16]。由于降水事件不是有就是无，所以TS评分是评估降水事件是否发生的较好的度量指标。降水检验分类如表1所示。

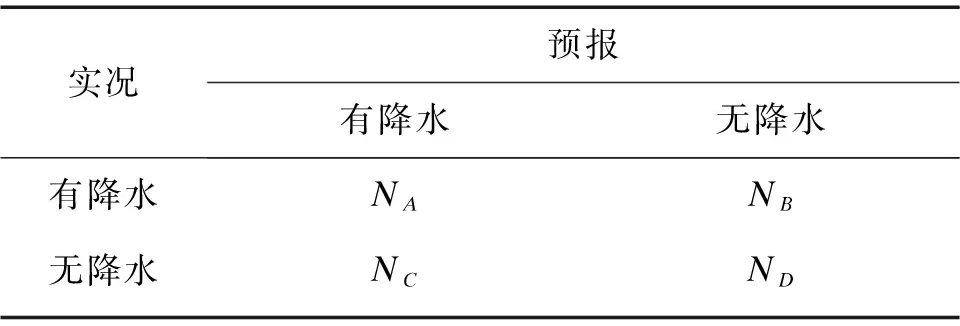
表1 降水检验分类表Table 1 Schematic contingency table for precipitation forecast test

TS的评分公式为：

(1)

预报偏差B的计算公式为：

(2)

式(1)—式(2)中，NA表示降水预报正确的次数；NB表示空报的次数，NC表示漏报的次数。TS评分越大表示预报的结果越好。预报偏差B为降水预报发生的次数和实况观测到降水发生的次数之比。当B=1时表示预报是无偏的，B>1时表示预报时存在空报的情况，而B<1时表示预报存在漏报的情况。本文TS评分值和B值为样本中各集合预报中心每个成员TS评分和B评分的平均值。

1.3 概率性预报检验方法

基于集合预报做出的概率预报，使得集合系统预报检验比较复杂，没有一个单独的评分方法或者检验技术可以全面地描述集合预报系统的性能，必须通过一系列的评分指标，才能从不同侧面完成集合预报的检验。一般地，集合预报可以从以下几个方面来检验[17]：(1)一致性(离散性)，从统计学意义上考虑观测值是否被包含于集合成员的特征分布之中。(2)预报的可靠性：从统计学意义上考虑事件的预报概率和观测出现频率是否一致。(3)准确性(分辨性鉴别能力)：预报结果是否与观测值一致。本文分别采用Talagrand分布和BS评分及其分解来描述集合预报的概率性误差特征。

为了得到概率预报，将不同预报中心内的各成员视为等权重的。在样本中每一个站点上，针对10.0 mm降水阈值计算概率预报，1则认为某一个降水阈值预报有降水发生，0则认为无降水发生。而预报有降水的成员个数与总集合预报成员个数的商被认为是这个站点上某一个阈值降水事件发生时的预报概率。实况降水的概率则是采用当某一阈值的降水事件发生时则观测概率记为1，降水事件不发生时观测概率记为0。

1.3.1 集合预报离散度检验—Talagrand分布

一个集合预报系统的重要检验指标是离散度检验。从统计学来看，在大多数情况下如果成员个数足够时，大气的真实状态应该包含在内。Talagrand等[18]提出一个好的集合预报系统中每一个预报成员发生的概率应该均等(即理想概率)，他们之间的离散度既不能太大，也不能太小，实况值应该是集合预报成员中的任意一个，所以Talagrand方法被认为是一种常用于检验集合预报系统离散度的简便方法。当一个集合预报系统有N个成员，将N个成员的预报从小到大进行排列，形成N+1个区间。当检验的样本足够多时，根据统计原理观测值会等概率的出现在(N+1)个区间中的每一个区间里。累计每个区间里观测站点的个数，并在每个站点上重复上述过程，则可在每一个区间中得到均匀一致的直方图，他们所对应的值即是理想概率，其值为1/N。

Talagrand分布的结果一般有以下3种形状。“L”型表明集合预报系统有偏差。若实况主要出现在集合降水预报的小值区域，说明系统有正的偏差。若实况主要出现在集合降水预报的大值区域，说明系统有负的偏差。“A”型表明实况主要出现在集合降水预报的中间区域，即系统的离散度太大。“U”型表明实况大多数出现在集合降水预报的两端，即系统的离散度太小。

1.3.2 Brier评分

Brier评分(Brier Score，BS)主要是对连续变量进行概率预报检验的一种指标。它在均方概率误差的基础上，还考虑到了概率预报的可靠性、分辨性和不确定性的特点[19-20]。BS评分的计算公式为：

(3)

式(3)中，fi是第i个样本事件发生的预报概率，其值在0—1之间。oi是第i个样本事件发生的观测频率，当观测到事件发生时，oi=1；当观测到的事件不发生时，oi=0。BS评分是负定向评分，且BS评分的数值在0—1之间，当BS值等于0表示集合预报系统概率预报最佳，值越小，集合预报系统的准确率越高。BS还可以分解为以下3项：

(4)

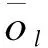
2 结果分析

2.1 辽宁省春季透雨的空间分布

图2为2016—2018年4—6月辽宁省10个站及以上24 h降水量超过10.0 mm的平均降水分布，即2016—2018年辽宁春季透雨降水分布特征。从图2可以看出，2016年平均降水量最大且分布最为均匀，大值区主要集中在大连、鞍山和营口地区；2017年辽宁省北部平均降水量较小，平均降水量大值区主要集中在辽宁省东部地区和大连地区；2018年平均降水量大值区主要集中在辽宁省的大连和朝阳地区。

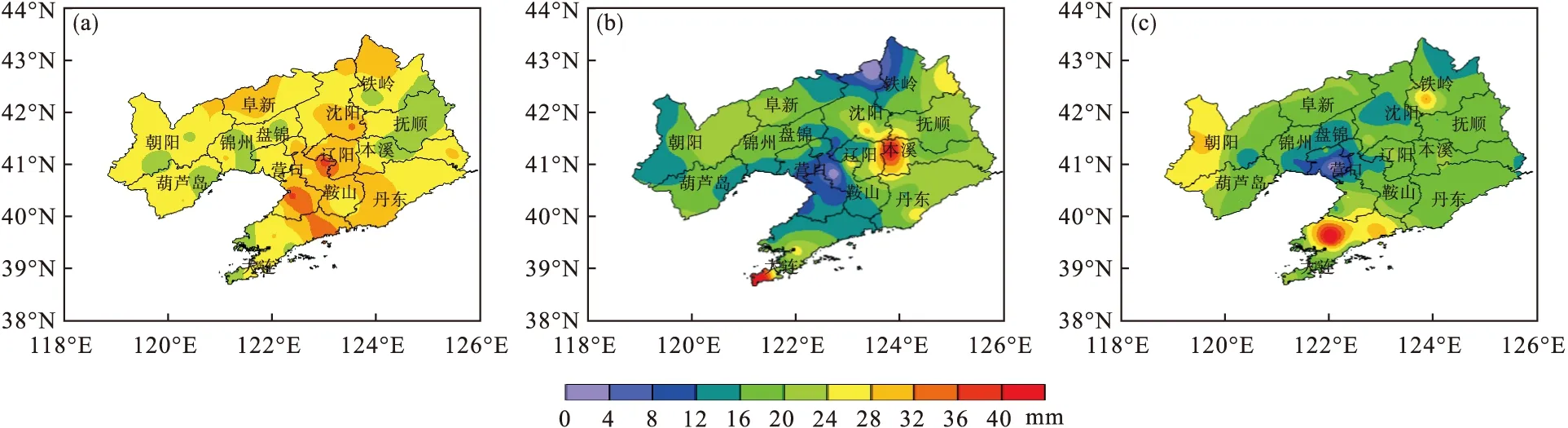
图2 2016年(a)、2017年(b)和2018年(c)4—6月辽宁省10个站及以上24 h降水量超过10.0 mm的平均降水分布Fig.2 Distributions of average precipitation of the 24 h precipitation exceeding 10.0 mm in more than 10 stations in Liaoning province during April to June in 2016(a),2017(b)and 2018(c)

2.2 降水确定性预报误差特征分析

根据三套集合预报系统2016—2018年4—6月辽宁省的降水预报值以及相应的实况值，考虑辽宁省春季透雨为降水阈值大于10.0 mm的情况计算3个集合预报中心的TS评分和预报偏差B值，其中2016—2018年3 a TS评分值和B值评分值的平均值。通过3个集合预报中心的TS评分和预报偏差B值可以看出(图3)，当降水阈值为10.0 mm时，3 a中ECMWF的TS评分值最大，分别为0.47、0.39以及0.37，而CMA在2017年和2018年TS评分值最小。通过3 a平均的TS评分值可知，ECMWF的TS评分值最大，其次是NCEP，最后是CMA。综上所述，ECMWF对于降水阈值为10.0 mm的TS评分值较高，预报效果最好。

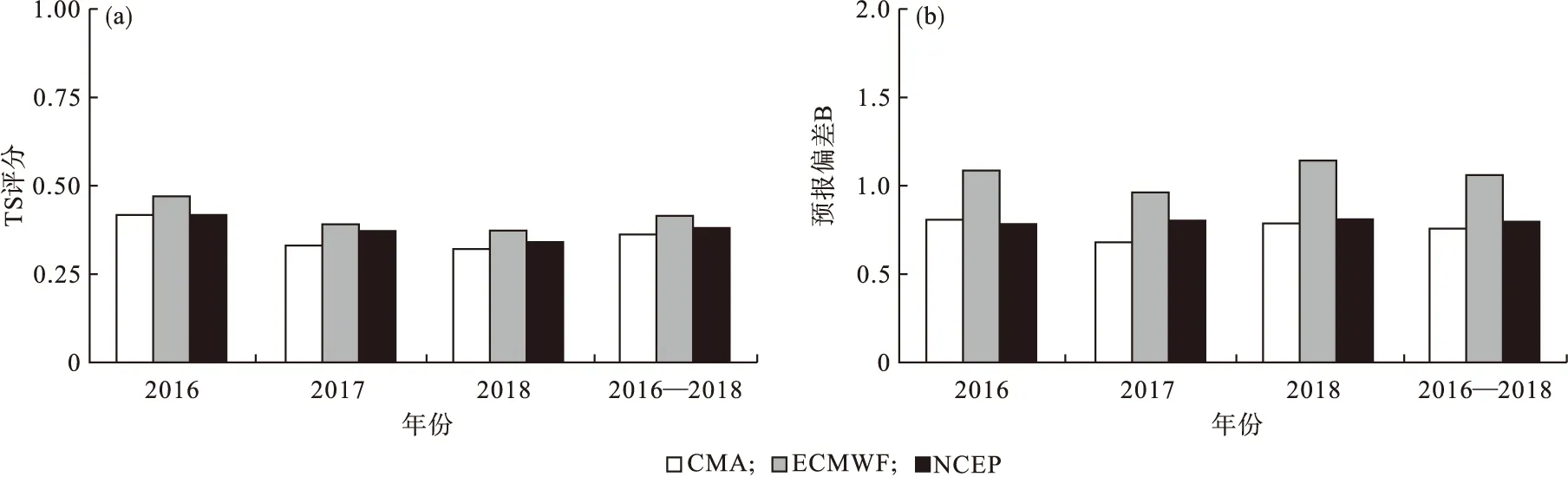
图3 2016—2018年4—6月以及此时段平均辽宁省三个集合预报中心在降水阈值为10.0 mm的降水预报TS评分(a)和预报偏差B(b)Fig.3 Threaten scores (a) and bias (b) of the forecasts for precipitation at thresholds of 10.0 mm and period average values from the three ensemble forecast centers during April to June from 2016 to 2018 in Liaoning province

通过分析3 a以及其平均的预报偏差B值可知，3 a中ECMWF在降水阈值为10.0 mm的预报偏差B值分别为1.10、0.97以及1.10。所以ECMWF的预报偏差B值相比CMA和NCEP两个中心，更接近于1，预报效果比较好。而CMA和NCEP两个中心预报偏差B值小于1，也就是说这两个中心对辽宁省春季透雨预报存在漏报。

2.3 降水概率性预报误差特征分析

2.3.1 Talagrand分布

图4为2016—2018年4—6月辽宁省3个中心24 h降水阈值为10.0 mm时的Talagrand分布，图4 24 h表示模式24 h间隔降水预报的概率值，灰色直线表示理想情况下的分布曲线。整体来看，模式预报的Talagrand分布与理想情况下的概率期望还存在一定的差距，3个中心的降水集合预报都呈“U型”分布，说明离散度不够，观测结果总是落在集合预报成员的最大值和最小值之外。也就是说各集合预报系统对量级较小的降水预报值偏大，空报率高；对量级较大的降水预报概率也高于理想概率，说明对极端降水的预报能力不足，极值偏小。将3个中心的降水预报的中间等级进行对比可以发现，ECMWF第4、5、6和第49、50区间的概率是在理想概率值附近。而CMA和NCEP只有第2区间。即观测值落在集合预报成员中最大值之外的概率，ECMWF的概率小于CMA和 NCEP。由此可以看出，ECMWF的离散性最好，CMA和NCEP次之。

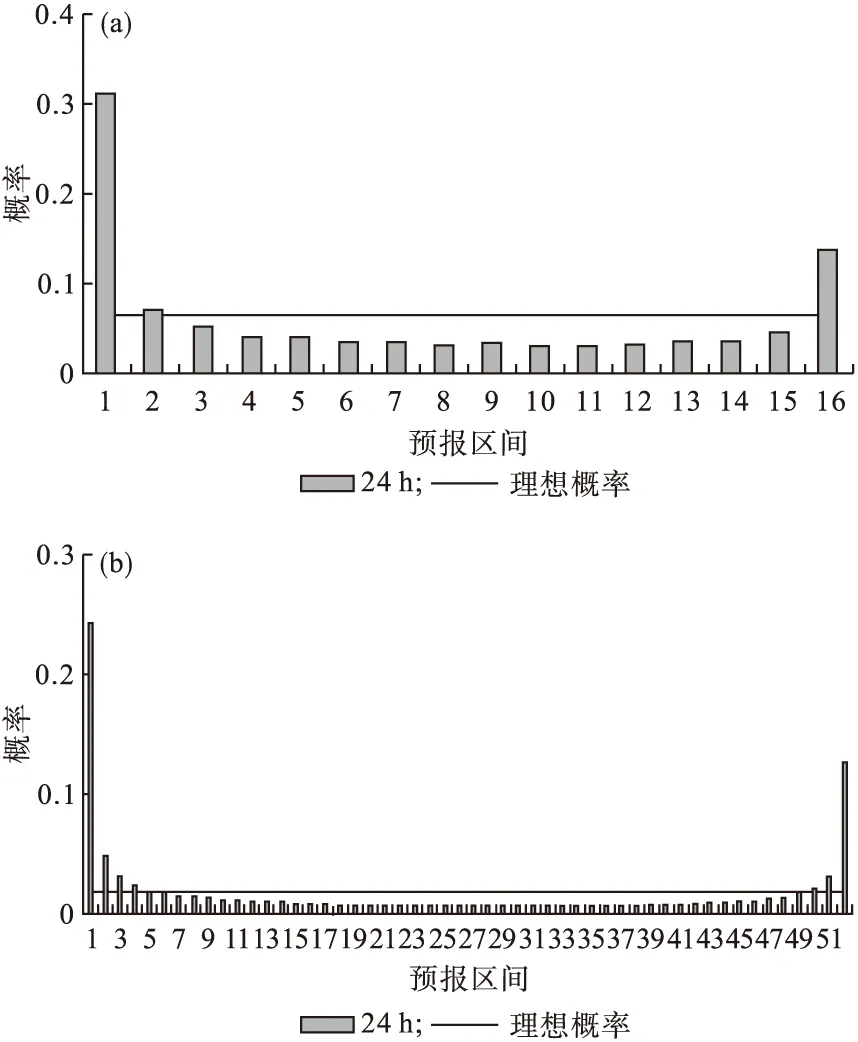
图4 2016—2018年4—6月辽宁省CMA(a)、ECMWF(b)、NCEP(c)在降水阈值为10.0 mm的Talagrand分布Fig.4 Talagrand distribution diagrams for forecasted precipitation at threshold of 10.0 mm from CMA (a),ECMWF (b),and NCEP (c) during April to June from 2016 to 2018 in Liaoning province

综上，CMA、ECMWF和NCEP这3个中心的集合预报系统离散度均具有偏小的特征，这在一定程度上导致实况值落在两端区间的概率比较大，实况值有较大的概率不落在集合预报系统中，因而容易产生降水预报偏差，影响预报效果。由于离散性表示集合预报成员之间的差异[21]，一个好的集合预报系统应是离散性检验结果较好的。因此，ECMWF相比CMA和NCEP预报质量更高。

2.3.2 Brier评分

Brier评分是检验集合预报准确性的一种概率预报评分方法。它综合考虑了不确定性、可靠性和分辨性，其值是负定向的，值越小，表示预报的质量越高。图5为2016—2018年4—6月以及此时段平均辽宁省降水阈值大于10.0 mm的情况下3个集合预报中心对于降水预报的BS评分。从图5可以看出，3 a中ECMWF的BS评分值均为最小,分别为0.03、0.02以及0.024，其预报质量最好，在2016年CMA的BS评分值小于NCEP，而在2017年和2018年NCEP的BS评分值小于CMA。而对于3 a平均的BS评分值，ECMWF最小，其次是NCEP，最后是CMA，也就是说ECMWF相比其他两个集合预报中心对于降水预报的效果更好。综上所述，ECMWF的概率预报误差小于CMA和NCEP， ECMWF集合预报的效果最好。

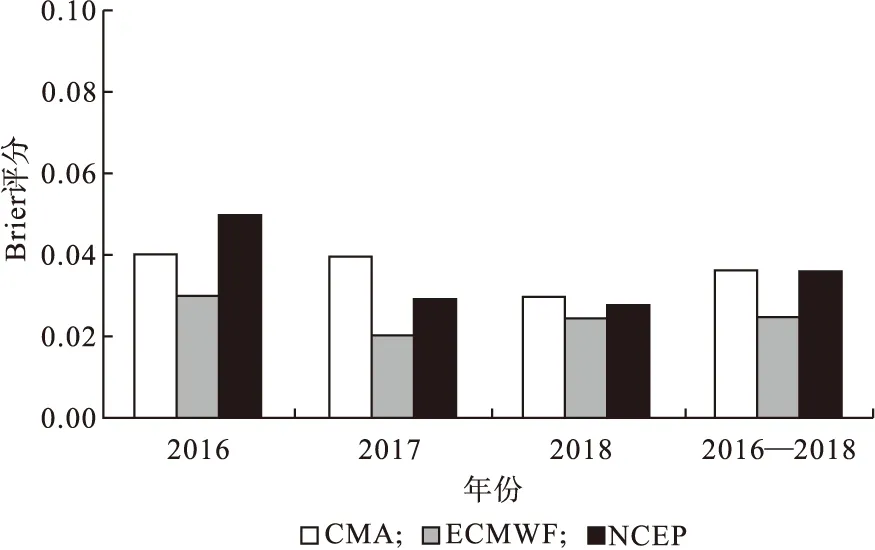
图5 2016—2018年4—6月以及此时段平均辽宁省三个集合预报中心在降水阈值为10.0 mm的降水预报BS评分值Fig.5 Brier scores (BS) of the forecasts for precipitation at threshold of 10.0 mm and period average values from the three forecast centers during April to June from 2016 to 2018 in Liaoning province

2.3.3 Brier分解评分

可靠性代表的是预报概率与观测频率的一致程度，其值越小表示可靠性越好。图6为2016—2018年4—6月以及此时段平均辽宁省降水阈值大于10.0 mm的情况下3个集合预报中心对于降水预报的BS可靠性评分。从图6可以看出，BS可靠性评分的大体趋势与BS评分值一致。将不同年份不同中心的BS可靠性评分值进行对比可知，3 a中ECMWF的BS可靠性评分值均为最小，预报质量最好。2016年CMA的BS可靠性评分值小于NCEP，而2017年和2018年NCEP的BS可靠性评分值小于CMA。而对于3 a平均的BS可靠性评分值，ECMWF最小，其次是NCEP，最后是CMA，即ECMWF相比其他两个集合预报中心对于降水预报的效果更好。

分辨性是度量预报频率与气候概率区别的程度，分辨性的值越大表示分辨性越好。图7为2016—2018年4—6月以及此时段平均辽宁省降水阈值大于10.0 mm的情况下3个集合预报中心对于降水预报的BS分辨性评分。由图7可以看出，对比研究时段内的3个集合预报中心，ECMWF的分辨性值要高于其他两个中心，而2016年分辨性值明显高于其他年份，有可能是因为2016年透雨样本数量较多造成的。综上所述，ECMWF分辨性最优，其次是NCEP，最后是CMA。

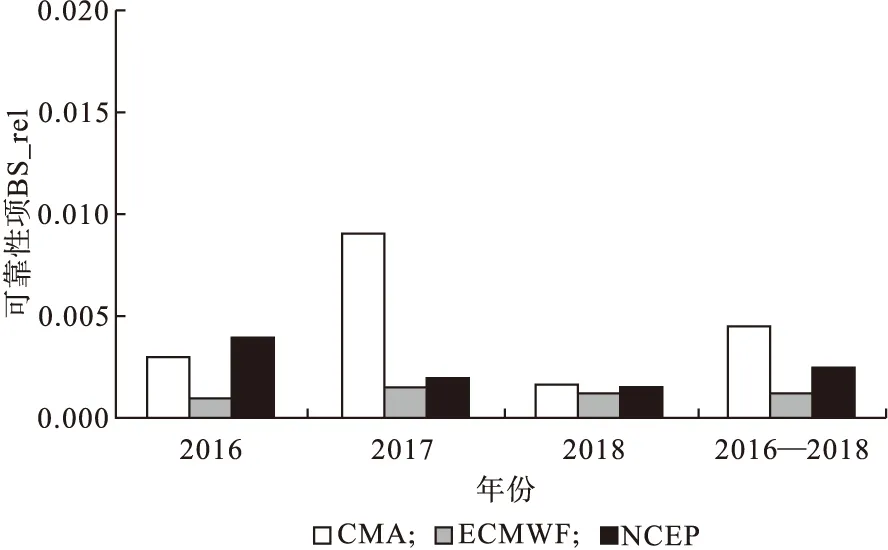
图6 2016—2018年4—6月以及此时段平均辽宁省三个集合预报中心在降水阈值为10.0 mm的降水预报BS可靠性评分值Fig.6 Reliability of brier scores (BS_rel) of the forecasts for precipitation at threshold of 10.0 mm and period average values from the three forecast centers during April to June from 2016 to 2018 in Liaoning province

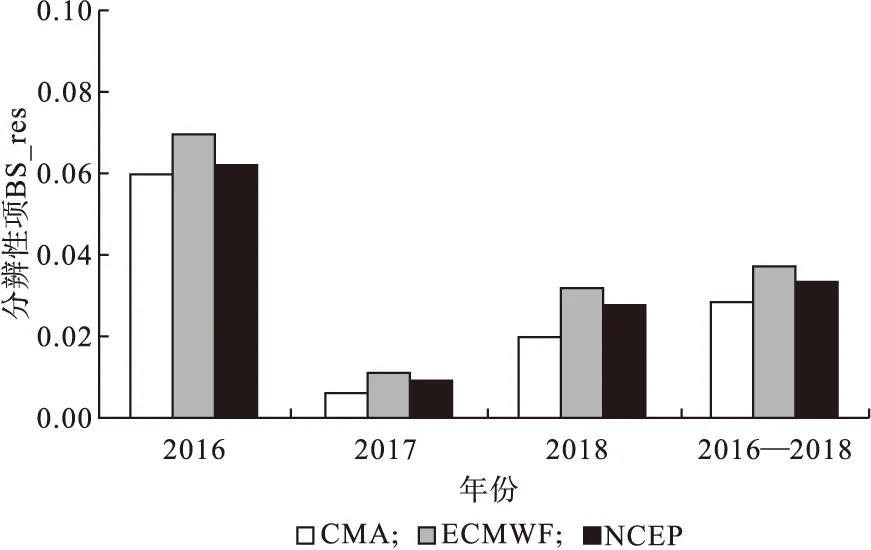
图7 2016—2018年4—6月以及此时段平均辽宁省三个集合预报中心在降水阈值为10.0 mm的降水预报BS分辨性评分值Fig.7 Resolution of brier scores (BS_res) of the forecasts for precipitation at threshold of 10.0 mm and period averagevalues from the three forecast centers during April to June from 2016 to 2018 in Liaoning province

3 结论与讨论

(1)由2016—2018年4—6月辽宁省的国家级地面气象站降水资料，以及同期的CMA、ECMWF和NCEP三套全球集合预报系统多成员的降水集合预报结果可知，ECMWF对于降水阈值为10.0 mm的TS评分值相比CMA和NCEP两个中心更高，预报偏差B值3个中心都偏小，但ECMWF比另外两个中心更接近于1，所以ECMWF相比其他两个预报中心的预报效果较好。

(2)总体上，集合模式对于辽宁省春季透雨预报的Talagrand分布与理想情况下的概率期望还存在一定的差距，3个集合预报中心的降水预报都呈U型分布，即三者的离散度均具有偏小的特征，实况值有较大的概率不落在集合预报系统中，因而容易产生降水预报偏差。

(3)根据BS评分及其分解评分可知，ECMWF对于降水阈值为10.0 mm的BS评分值最小，其次是NCEP，最后是CMA，说明ECMWF预报效果最好。BS可靠性评分值和BS分辨性评分值同样表现出ECMWF高于CMA和NCEP。

(4)本文现阶段利用3个集合预报中心3 a的24 h降水集合预报资料对辽宁省春季透雨预报的结果进行误差特征分析，但在日后的研究工作中应采用更长预报时效的集合降水预报进行更为详尽的分析研究。