含峭壁V形峡谷对地震SH波散射的解析解

张宁， 潘家琐， 代登辉， 高玉峰*

1 河海大学岩土力学与堤坝工程教育部重点实验室， 南京 210098 2 河海大学土木与交通学院， 南京 210098

0 引言

当地震波遇到峡谷、高山等局部地形时会发生散射，散射波、入射波和反射波的相互作用会引起地震动的放大或衰减，称为地形效应(周红等，2010；田林等，2012).自从美国圣费尔南多地震记录的异常放大现象(Trifunac and Hudson, 1971)得到关注之后，国内外大量的地震实测记录和现场震害观测进一步证实了地形效应的存在(王海云和谢礼立,2010；Hough et al., 2010；李平等, 2016).

为了揭示地形效应机理，地震学和土木工程领域学者开展了地表地形对地震地面运动影响规律的理论研究，包括数值模拟和解析分析两类方法.数值研究众多，例如有限差分法(Boore, 1972)、有限元法(廖振鹏和刘晶波,1992；章小龙等, 2017)、谱元法(李孝波等，2014；于彦彦等,2017；贺春晖等,2017)、边界方法(林皋和关飞,1990；曹军等,2004；巴振宁等,2017；Liu et al., 2018)及混合方法(Zhang and Zhao,1988；金峰等,1993；Zhou and Chen, 2006).数值方法可以模拟任意复杂地形情况，但其计算精度往往需要解析解的校准.解析方法主要是波函数展开法，Trifunac(1973)提出的半圆形峡谷对地震SH波散射的波函数级数解成为早期经典的解析解，随后涌现出更多针对不同地形的解析解，如半椭圆形峡谷(Wong and Trifunac, 1974)、圆弧形峡谷(Yuan and Liao, 1994)、圆弧形饱和土峡谷(李伟华和赵成刚,2003)、圆弧形层状峡谷(梁建文等,2003)、圆弧形层状沉积谷(张郁山,2008，2010)、去底半圆形峡谷(Tsaur and Chang, 2009)、U形峡谷(Gao et al., 2012)、径向非均质半圆形峡谷(Zhang et al., 2017, 2019)等.这些解析解为数值方法提供了验证基准，并且引领了新型数值方法(Dai et al., 2019)的发展.

图1 含峭壁V形峡谷示例：亚利桑那州北部Glen峡谷Fig.1 An example of V-shaped canyon with cliffs: Glen canyon in northern Arizona

由于V形峡谷分布广泛，这类地形对地震波的散射问题得到了大量的数值(Sánchez-Sesma and Rosenblueth, 1979；赵崇斌等,1988)和解析(Tsaur and Chang, 2008；Tsaur et al., 2010；Zhang et al., 2012a，b；Gao and Zhang, 2013)研究.在长期的地质演变中，由于峡谷侧壁的地应力集中，这种峡谷最终倾向于演变成含峭壁V形峡谷，典型的例子如亚利桑那州北部科罗拉多河的Glen峡谷(如图1).然而，含峭壁V形峡谷地形效应研究尚未见报道.实际上，诸多峡谷具有峭壁，有必要开展含峭壁峡谷地形对地震波的散射特性研究.因此，本文采用波函数展开法提出了含峭壁V形峡谷对平面SH波散射的解析解，重点考察了上部峭壁对其地形效应的影响.

1 模型和理论推导

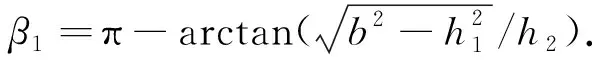
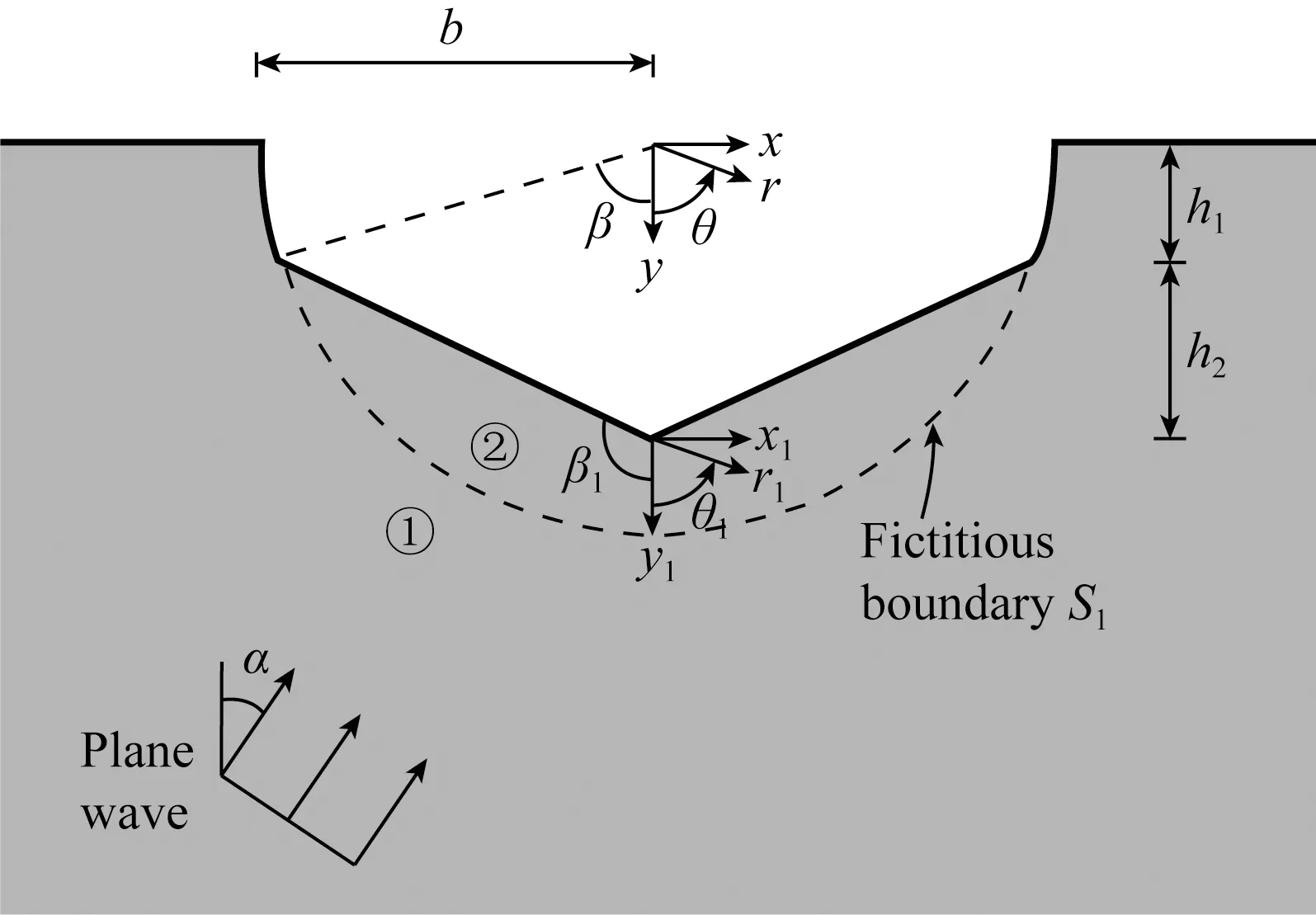
图2 平面SH波作用下含峭壁V形峡谷的二维模型Fig.2 2D model of a V-shaped canyon with cliffs subjected to a plane SH waves

对于稳态反平面问题，可省略时间因子e-iω t，则模型两个区域的稳态波场uj满足亥姆霍兹方程(Pao and Mow, 1973)：

(1)

其中j=1,2,分别表示区域①和②，k=ω/cs表示波数.

除了亥姆霍兹方程，两个区域的波场uj还需要满足水平地表、峡谷表面和峭壁表面的应力自由条件：

(2)

(3)

(4)

另外，根据连续介质假设，由虚拟边界S1分割而成的两区域的位移和应力均须满足连续性条件：

u1(r,θ)=u2(r,θ),r=b, 0≤|θ|≤β，

(5)

(6)

公式(5)和(6)可保证两区域之间的位移和应力匹配.

区域①的波场包含两部分(自由场和散射场)：

u1=uf+us,

(7)

自由场可以表示为

uf(r,θ)=exp[-ikrcos(θ+α)]

+exp[ikrcos(θ-α)]，

(8)

利用Jacobi-Anger展开公式：

(9)

其中εn是纽曼因子(ε0=1，εn=2,n≥1)，Jn(·)是n阶第一类贝塞函数，公式(8)中的自由场uf可以展开成：

(10)

模型物理意义明确，散射波由河谷处产生、向无穷远处传播，为了得到散射波场的唯一解，其应该满足无穷远处Sommerfeld辐射条件：

(11)

通过分离变量法求解公式(1)并排除不满足辐射条件(11)的波场后可以得到：

(12)

在区域②中，满足峡谷底部应力自由条件(公式(3))的驻波场u2可以表示为

(13)

其中Cn和Dn为待求系数，ν=π/(2β1).

为了便于问题的解决，需要用Graf加法公式将局部坐标系(r1,θ1)中的驻波场u2转化到整体坐标系(r,θ)中.推导得到相应的变换公式为

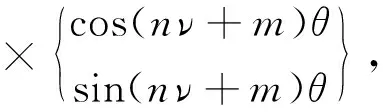
(14)

其中h=h1+h2.

将公式(14)代入公式(13)，驻波场u2可以表示为

+1)ν+m]θ.

(15)

至此，利用前述区域分解策略完成了两区域波场的构建，且两区域波场分别自动满足水平地表应力自由条件(公式(2))和峡谷表面应力自由条件(公式(3)).然而，波场的四组未知系数An、Bn、Cn和Dn仍然待定，需要利用余下的峭壁应力自由条件(公式(4))和虚拟边界连续条件(公式(5)和(6))完成求解，即区域匹配技术：

首先，补充区域②在峭壁上的零应力条件，获得区域②在与区域①的半圆形交界面上的分段应力函数：

(16)

据此可将峭壁应力自由条件(公式(4))和虚拟边界应力连续条件(公式(6))合并为

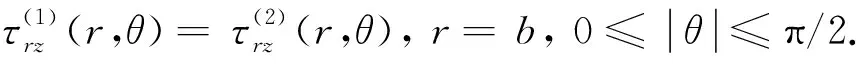
(17)

对式(17)两边同时关于θ在区间[-π/2,π/2]积分，并利用三角函数在此区间的正交性，整理可得关系式：

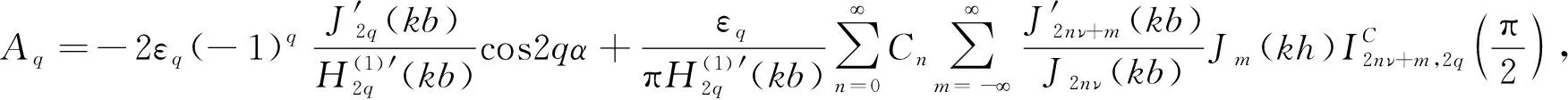
(18)

(19)

(20)

(21)

然后，利用虚拟边界S1上的位移连续条件(公式(5))，将两区域位移场在区间[-β,β]上积分得：

(22)

(23)

最后，将公式(18)和(19)分别代入公式(22)和(23)，得到下面仅和Cn、Dn有关的两个方程组：

(24)

(25)

将各无穷级数进行截断、保留有限项之后即可进行未知系数计算(n、m和p分别截取N、M和P项).求解公式(24)和(25)可得到系数Cn和Dn，随后通过公式(18)和(19)求得An和Bn.得到这些未知系数后，半空间中的波场即已知.

关于N、M和P的取值，其中N代表级数解的级数项数量，需要通过级数解收敛测试确定.本文选取了峡谷表面5个代表性位置进行了收敛测试.图3给出了参数对应α=30°、h1/b=h2/b=1/3和η=4的收敛测试结果.从图3中可以看出，随着N的逐渐增大，地表位移逐渐收敛至一个固定值.通过多频率下的收敛测试，本文采用N=25即可获得精确的结果.M和P要保证驻波场u2和自由场uf的坐标变换精度，分别利用公式(14)和(9)的满足情况确定其数值为M=150，P=150.

2 验证

为了方便起见，首先定义本文位移幅值|u|和无量纲频率η：

(26)

(27)

其中Re(·)和Im(·)分别表示复位移的实部和虚部，λ表示入射SH波波长.

当h1/b=0时，含峭壁的V形峡谷可以退化为V形峡谷；当h2/b=0时，可退化为去底半圆形峡谷.Tsaur和Chang(2008，2009)分别给出了V形峡谷和去底半圆形峡谷的解析解，因此可以用来验证本文结果的准确性.

图4将本文的结果与Tsaur和Chang(2008)进行了对比，对应参数为h1/b=0，h2/b=1/2，η=1.图5将本文的结果与Tsaur和Chang(2009)进行了对比，参数为h1/b=1/2，h2/b=0，η=1.通过4个不同入射角度α=0°、30°、60°和90°下结果的良好吻合情况，验证了本文方法的准确性.

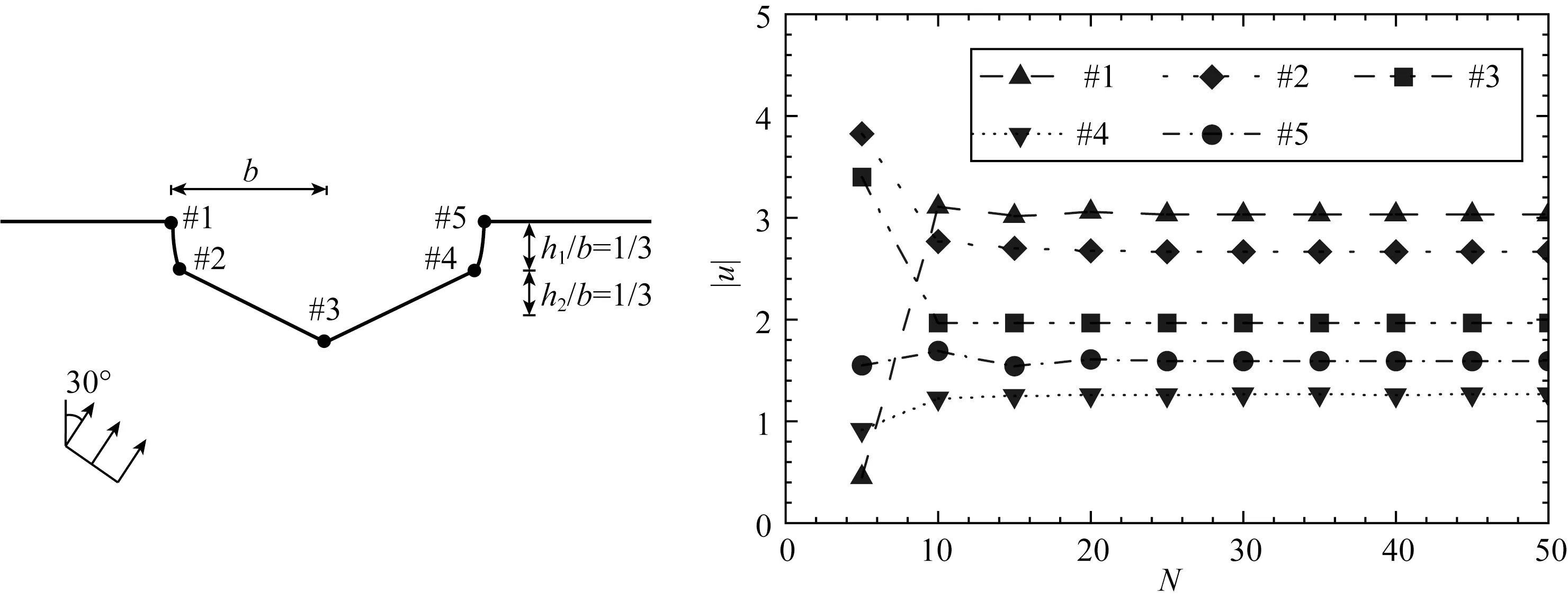
图3 峡谷表面五个代表性位置的地表位移收敛测试图(α=30°, h1/b=h2/b=1/3, η=4)Fig.3 Convergence tests at five representative positions on the canyon surface (α=30°, h1/b=h2/b=1/3, η=4)

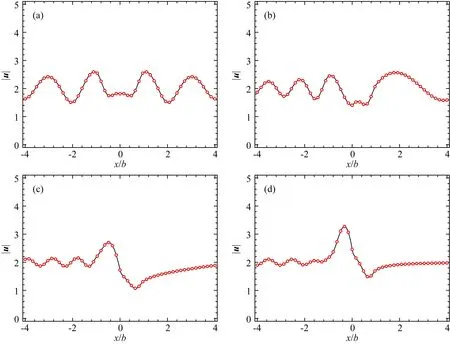
图4 本文结果(实线，对应参数：h2/b=0，h2/b=1/2，η=1)与Tsaur和Chang(2008)中无峭壁V形峡谷相应结果(点线)的比较(a) α=0°; (b) α=30°; (c) α=60°; (d) α=90°.Fig.4 Comparison between the solution of this study (solid lines) when h1/b=0, h2/b=1/2, η=1 and the corresponding results (dotted lines) of the V-shaped canyon without steep cliffs given by Tsaur and Chang (2008)

为了进一步检验本方法的正确性和实用性，继续采用退化V形峡谷模型模拟中国台湾翡翠峡谷台阵的地震动并与实测结果进行对照.根据Huang和Chiu(1995)对1992年花莲地震时翡翠河谷台阵实测地震动的分析，编号为SC1的台站地震记录相比SC4加速度峰值放大了2.69倍.

翡翠台阵所在的河谷剖面如图6a所示，利用本文方法为之建立V形峡谷模型(b=563 m，d=300 m，h1=0 m).由于1992年花莲地震入射波数据缺失，本文采用PGA=0.2g的集集地震波作为入射波，利用本文模型求得台站SC1和SC4处的地震动频域传递函数，然后据此得到台站SC1和SC4的地震动加速度时程，如图6b所示(频域转时域方法参见Dai et al.，2019).其中台站SC1和SC4处的模拟地震动PGA分别为0.3324 g和0.1256 g，即SC1相对于SC4放大2.65倍，与前述实测2.69倍基本一致.可见，本方法可以较好地刻画峡谷对地震动的差异放大规律.

图5 本文结果(实线，对应参数h2/b=1/2，h2/b=0，η=1)与Tsaur和Chang(2009)中去底半圆形峡谷的相应结果(虚线)的比较(a) α=0°; (b) α=30°; (c) α=60°; (d) α=90°.Fig.5 Comparison between the solution of this study (solid lines) when h1/b=1/2, h2/b=0, η=1 and the corresponding results (dotted lines) of truncated semicircular canyon given by Tsaur and Chang (2009)

图6 本文方法对中国台湾翡翠河谷地震动的模拟(a) 翡翠河谷模型简图(据Huang and Chiu, 1995)； (b) 集集地震入射下SC1台站和SC4台站SH波地震动加速度时程模拟结果.Fig.6 Simulation of the ground motions for the Feitsui Canyon, Taiwan, China(a) Schematic diagram of Feitsui Canyon model (modified from Huang and Chiu, 1995)； (b) The calculated SH ground accelerations at positions SC1 and SC4 under the incidence of the Chi-Chi earthquake.

3 数值结果与讨论

本文聚焦上部峭壁对峡谷地形效应的影响，故将参数h2/b设为固定值1/3，从而使得h1/b有较大的变化范围.图7—图9分别为对应3个入射波无量纲频率η=0.5、1和4的峡谷地表位移幅值结果，每个无量纲频率结果都包含4个不同入射角度(α=0°,30°,60°,90°)，实线结果对应h1/b=0，虚线对应h1/b=1/3，虚实线对应h1/b=2/3.为了方便比较，x/b的计算范围选取为-4到4.

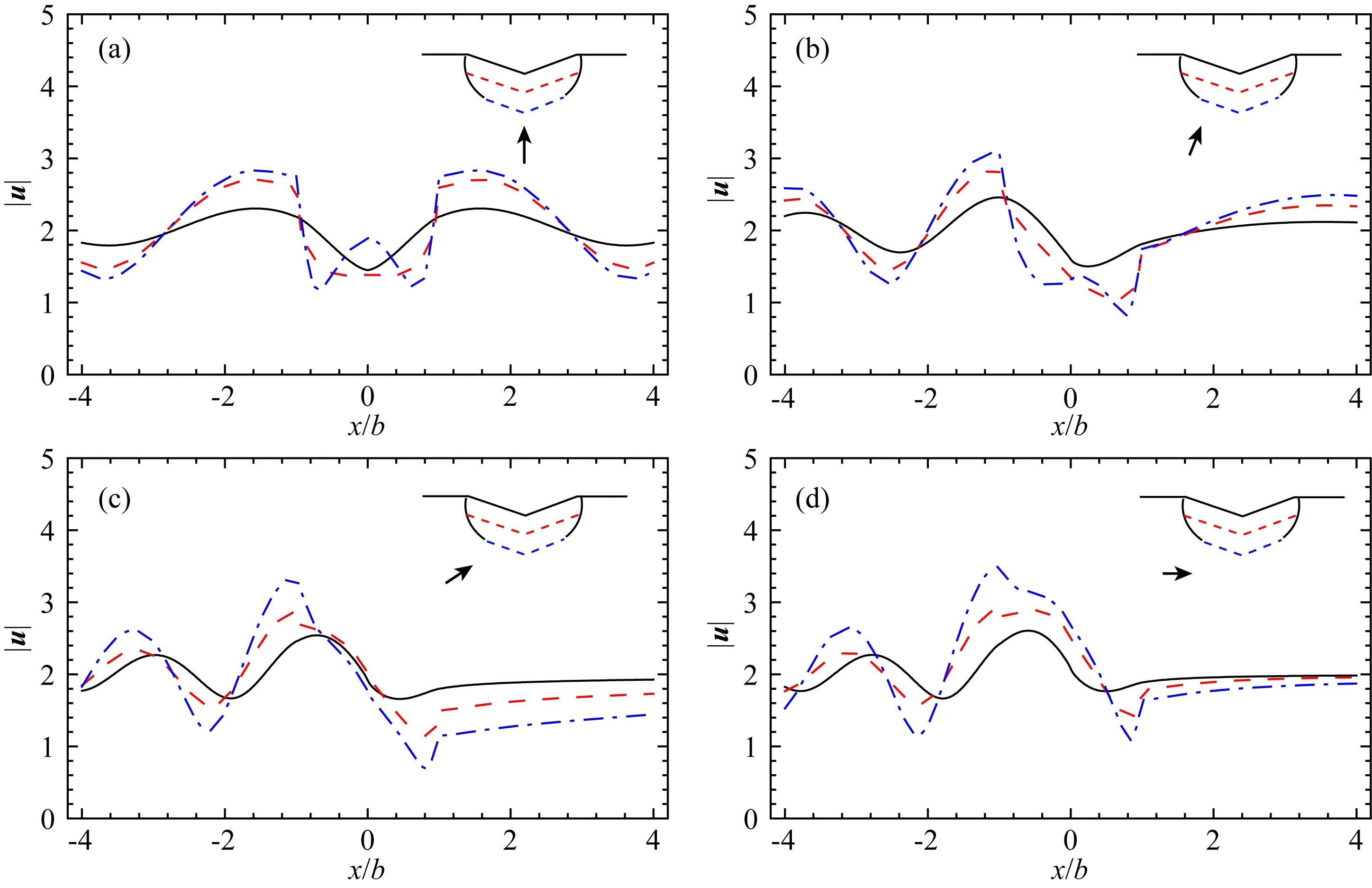
图7 对应η=0.5和不同入射角度的地表位移幅值结果(a) α=0°; (b) α=30°; (c) α=60°; (d) α=90°.黑色实线对应h1/b=0，h2/b=1/3；红色虚线对应h1/b=1/3，h2/b=1/3；蓝色点划线对应h1/b=2/3，h2/b=1/3.Fig.7 Surface displacement amplitudes at four different incident angles and η=0.5(a) α=0°; (b) α=30°; (c) α=60°; (d) α=90°. h1/b=0, h2/b=1/3 (black solid lines), h1/b=1/3, h2/b=1/3 (red dashed lines), h1/b=2/3, and h2/b=1/3 (blue dotted lines).

图8 对应η=1和不同入射角度的地表位移幅值结果(a) α=0°; (b) α=30°; (c) α=60°; (d) α=90°.黑色实线对应h1/b=0，h2/b=1/3；红色虚线对应h1/b=1/3，h2/b=1/3；蓝色点划线对应h1/b=2/3，h2/b=1/3.Fig.8 Surface displacement amplitudes at four different incident angles and η=1(a) α=0°; (b) α=30°; (c) α=60°; (d) α=90°. h1/b=0, h2/b=1/3 (black solid lines), h1/b=1/3, h2/b=1/3 (red dashed lines), h1/b=2/3, and h2/b=1/3 (blue dotted lines).

图9 对应η=4和不同入射角度的地表位移幅值结果(a) α=0°; (b) α=30°; (c) α=60°; (d) α=90°.黑色实线对应h1/b=0，h2/b=1/3；红色虚线对应h1/b=1/3，h2/b=1/3；蓝色点划线对应h1/b=2/3，h2/b=1/3.Fig.9 Surface displacement amplitudes at four different incident angles and η=4(a) α=0°; (b) α=30°; (c) α=60°; (d) α=90°. h1/b=0, h2/b=1/3 (black solid lines), h1/b=1/3, h2/b=1/3 (red dashed lines), h1/b=2/3, and h2/b=1/3 (blue dotted lines).

从图7—图9的结果可以看出，含峭壁V形峡谷的地表位移幅值在自由场位移幅值2上下波动(|u|>2表示放大，|u|<2表示减小)，峡谷峭壁对地表位移幅值具有重要影响.一方面，峭壁使得地震放大效应更为显著，通过比较h1/b=2/3和h1/b=0两种情况，可以发现含峭壁峡谷的地表位移幅值可达不含峭壁峡谷的2倍.另一方面，随着峭壁深度h1/b从1/3增大至2/3，位移振幅的最大值增大，而位移振幅的最小值减小.总之，峭壁对V形峡谷地形效应具有显著的增强作用，这意味着在地震作用下峭壁峡谷周边的建筑物将会遭受更为剧烈的振动，可能会造成更大的震害.

对于地震波竖向入射的情况(如图7a、图8a和图9a所示)，由于波的聚焦，地表位移幅值的最大值往往发生在峡谷两肩.不同于具有对称性的竖向入射结果，地震波斜入射的情况(图7(b—d)、图8(b—d)和图9(b—d))展示出左右不对称的地表位移幅值.迎波侧比背波侧的位移幅值波动得更加频繁，随着入射角度的增加，这种不对称表现得更加明显.在小角度斜入射(α=30°)的情况下，迎波侧的位移振幅仅略大于背波侧，而对于大角度斜入射(α=60°, 90°)的情况，两侧差别更加明显.随着无量纲频率η的增大，位移振幅的放大和减小越来越明显，说明峡谷成为一个有效的障碍物，短波穿越峡谷到达对岸的能力越来越弱.在图7(b—d)、图8(c—d)和图9d中，阴影区的位移幅值曲线趋于平稳，即体现了峭壁峡谷的滤波屏蔽效应.

图10展示了在三种入射角度下V形峡谷地表位移幅值随着无量纲位置x/b和无量纲频率η的变化情况，其中图10(a—c)是不含峭壁的情况(h1/b=0)、图10(d—f)是含峭壁的情况(h1/b=1/3).图中可见，随着无量纲频率的增大，含峭壁峡谷的地形放大形态趋于复杂.在同一入射角下，峭壁的存在使得峡谷两侧表现出更为明显的放大效应，也就是说峭壁的出现对峡谷地形效应有加剧作用.

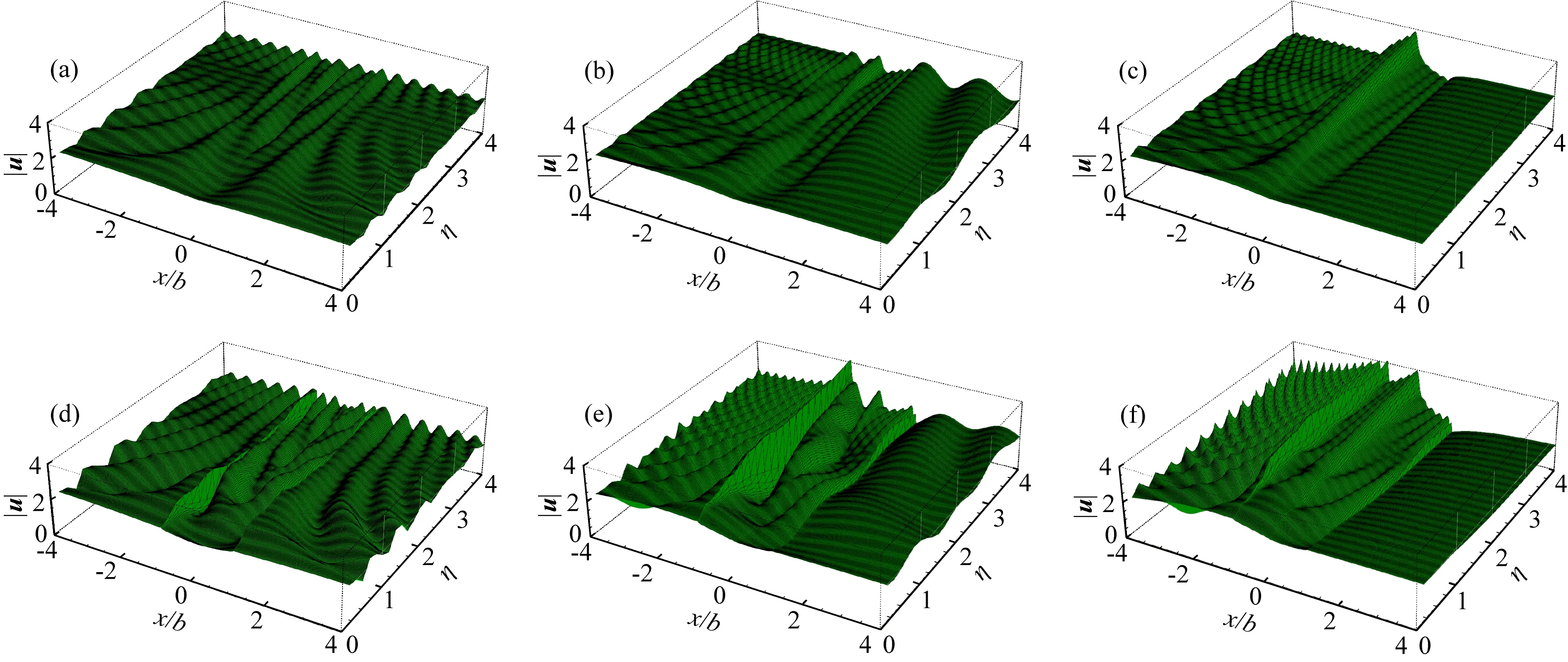
图10 不同角度下含峭壁和不含峭壁峡谷地表位移幅值随位置x/b和无量纲频率η的变化图(a) α=0°，h1=0，h2=1/3; (b) α=45°，h1=0，h2=1/3; (c) α=90°， h1=0，h2=1/3; (d) α=0°，h1=1/3，h2=1/3; (e) α=45°，h1=1/3，h2=1/3; (f) α=90°，h1=1/3，h2=1/3.Fig.10 Ground surface displacement amplitudes as a function of position x/b and dimensionless frequency η for canyons with and without steep cliffs at four different incident angles

4 结论

本文提出了含峭壁V形峡谷对地震SH波散射的波函数级数解，揭示了含峭壁V形峡谷对地震动的地形放大效应.本文解析模型可退化为不含峭壁的V形峡谷和去底半圆形峡谷两个已有解析模型，通过退化计算验证了本文方法.计算结果表明上部峭壁对峡谷地震动具有重要影响，峭壁峡谷(h1/b=2/3)较无峭壁峡谷(h1/b=0)对地表位移幅值的放大差异可达200%，且较陡的峭壁明显加剧峡谷的地震放大效应，也就增加了周围建筑物的震害风险，值得工程师的关注.本文结论基于二维峡谷场地SH波散射模型，关于峡谷场地的三维效应以及P波和SV波等其他类型地震波的散射特征，尚需进一步探索.