一种改进SURF 特征匹配的装配工件快速识别方法

张明路，王 帅，张小俊，高 涵

（河北工业大学 机械工程学院，天津300130）

1 引言

为了提高机械臂抓取装配工件过程中的识别效率和准确度，依托机器视觉的物体识别抓取系统逐渐得到应用和发展。在获取工件图像过程中由于存在尺度、光照、旋转等因素干扰，难以实现对物体的准确识别。基于局部特征的图像描述子具有抗干扰能力强，鲁棒性好的优点，成为图像匹配、识别的主要提取信息。

其中文献[1]提出一种加速版的特征提取算法—SURF（Speeded-Up Robust Features），该方法采用基于Hessian 矩阵的特征检测算子，对特征提取速度有一定的提高，但是距离图像处理实时性要求还有一定差距，匹配准确度还不够高。文献[2]中提出基于双向K 最近邻搜索方法，来进行特征点的预匹配，之后再进行RANSAC 算法的精匹配，但是该方法在使用双向检索的过程中并没有减少特征点之间距离的计算量，在匹配阶段同样对于特征点的筛选没有经过模型的优化，导致匹配时间缩短有限。文献[3]提出一种基于加速Hessian 矩阵特征检测器算法（H_SURF），实现了在SURF 特征检测阶段速度的提高，但是该方法需要对不同的应用场景设置不用的Hessian 阈值，需要手动调节的参数较多，并且在光照变换较大的情况下准确率明显降低。文献[4]将SURF 算法应用于高光谱影像端元的提取中，提出了在多维尺度空间中寻找端元的新算法，该算法在精度和鲁棒性方面有较好的效果。文献[5]利用图像分块和SURF 特征相结合，将图像分割成不同的块，在人脸特征识别中取得了较好的效果。文献[6]提出了一种线性化SURF 特征检测分类器在保证特征点尺度不变性的前提下提高特征点之间的差异性，在速度上相比原算法提高了，但减小了图像的匹配区域。文献[7]中利用SURF 特征描述子的稳定性，采用交叉匹配策略来消除错误的匹配点对，并运用RANSAC 算法进行模型估计，最终提高了图像匹配融合的效率。文献[8]提出一种结合FAST 特征检测、SURF 特征向量提取以及最近邻查询的方法来进行特征点的快速查询和匹配，特征提取较快，但是目前可应用在交通车辆领域，算法移植性差。文献[9]采用Canny 边缘检测以及形态学处理来对对SURF 算法进行改进，提高了匹配的稳定性，但是算法光照、视角变换下的准确度还有待提高。

从工件的匹配过程出发，为解决大量SURF 特征点匹配时计算欧氏距离[10]而导致效率低的问题，提出构建基于词袋模型[11-12]的物体描述向量模型来改进的SURF 特征的匹配过程，从而来提高工件识别速度。

2 算法简介

2.1 SURF 特征检测与描述模型

2.1.1 积分图像的计算

在SURF 特征的检测[13]过程中，为了加快算法的计算速度，采用了积分图像的概念。通过图像不同区域像素值的差值来进行图像的卷积计算。积分图像的概念，如图1 所示。阴影处的面积为ΣABCD。积分图像计算公式，如式（1）所示。

式中：A、B、C、D—从图像左上角到相应点的区域像素值之和。

图1 积分图像示意图Fig.1 Schematic Diagram of Integral Image

2.1.2 基于Hessian 矩阵的极值点检测

首先利用Hessian 矩阵对图像进行特征点的检测，每个像素点Hessian 矩阵行列式的响应值大小决定了该像素点是否为极值点。同时为了保证检测出来的特征点具有尺度不变性，SURF算法将高斯拉普拉斯算子（LOG）与Hessian 矩阵行列式计算相结合，保证了利用Hessian 矩阵行列式检测出来的特征点具有尺度不变性。其Hessian 矩阵表达式为：

式中：Lxx（x，σ）—高斯二阶微分函数在图像（x，y）点处与图像的卷积，其余三项含义类似。

将图像与高斯函数卷积计算模板化，这样既可以保证高斯滤波函数的有效性同时又可以提高算法的运行效率，这里采用差分高斯滤波模板（DOG）来代替LOG 滤波模板，初始模板大小为9×9，滤波系数为σ=1.2，用加权之后的DOG 模板来代替LOG 滤波模板，如图2 所示。得到x、y、xy 三个方向的二阶微分响应的分别是Dxx、Dyy、Dxy，来代替Lxx、Lyy、Lxy，之后用积分图像的概念来计算响应的值。

图2 DOG模板代替LOG 模板Fig.2 DOG Template Instead of LOG Template

最后得到Hessian 矩阵其行列式的计算公式为：

式中：ω—权值，平衡近似代替的误差。满足一定阈值条件的det（H）值，判断为极值点。

2.1.3 尺度图像金字塔的构建

为了获得尺度不变的特征点，需要进行尺度空间的构建，SURF 算法中通过改变盒子滤波器的大小来实现获得3 组12 层的尺度图像。同时在改变模板尺寸的同时也改变高斯滤波系数σ的值来实现构造尺度图像金字塔的效果，在不同的尺度图像上进行特征点的检测。

2.1.4 SURF 特征点的定位与描述

在上一步中检测出来的特征点通过阈值筛选，然后进行非极大值抑制，检测模型，如图3 所示。在3×3×3 的邻域内进行特征点的计算，得到满足条件的特征点并且得到特征点的位置。

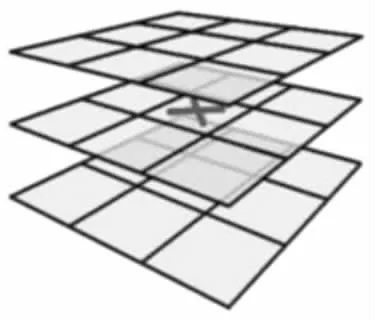
图3 极值点检测邻域Fig.3 Detection of Neighborhood by Extremal Points

然后利用特征点周围6s（s 为特征点所在的尺度）邻域内像素的Haar 小波响应来计算特征点的x 与y 方向的响应，然后使用张角为60°的扇形区域进行旋转滑动，寻找响应值最大的方向作为特征点的主方向。

3 基于改进SURF 特征匹配的物体识别模型

在图像物体识别过程中，传统SURF 算法通过计算大量特征点之间的欧氏距离并通过判断相邻两个特征点之间的距离比值来确定粗匹配的特征点，并通过优化算法计算出最优的单应性变换矩阵。在图像特征点数量较多的情况下，该过程会大大增加特征点匹配所用的时间。因此，改进算法在特征点匹配阶段在检测到的特征点基础上通过构建目标物体描述向量来进行匹配，省去较多的距离计算以及筛选步骤，从而实现提高物体识别速度的目的。

3.1 基于词袋模型的物体描述向量的构建

3.1.1 基于K-means 聚类的目标物体描述模型构建

模板图像通过SURF 算法提取特征点之后，通过K-means聚类算法[14]将模板图像检测到的特征点进行分类，为了使得分类能准确的描述目标物体，同时减少冗余类别的计算，初始值K 取为特征点维度的四分之一即16。

选择初始特征点时根据特征点的Hessian 特征值响应大小，将响应值的最大值到最小值均分为4 个区间，每个区间随机抽取4 个特征点作为种子点，根据特征点之间的欧氏距离进行分类。

式中：di—两特征点之间的距离；xj、yj—特征点向量的元素坐标；P—给定阈值，M=64。

图4 目标物体的描述向量构造流程图Fig.4 The Flow Chart of Description Vector of Target Object

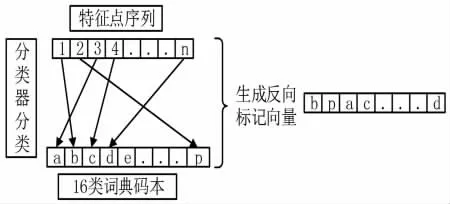
图5 反向标记流程图Fig.5 Reverse Marking Flow Chart

3.1.2 待检测物体图像模型的构建

待检测图像生成的描述向量维度较大，为了实现快速的匹配将向量p 分成4 等分，即p1、p2、p3、p4，四个通道。

3.2 基于物体描述向量的目标物体匹配与识别模型

（1）将向量p1，p2，p3，p4分别从第一个元素开始以向量O 的长度为区间长度，以ε 为采样步长，将向量pi（1≤i≤4）分为t 个不同的区间。分别统计各自区间上不同码本的种类和各自的数量，得到一组统计向量ti。

（2）将统计向量ti与向量O 分别计算包含的码本种类h 和各类码本的数量g，生成词典码本直方图。

（3）比较向量O 生成的码本直方图与向量ti生成的直方图，计算余弦相似度，给定阈值Q，满足阈值条件的作为匹配向量。

（4）选取匹配向量中的4 对特征点计算单应性转换矩阵，求解矩形框的中心坐标和边界宽度，用来实现目标物体的有效框选。

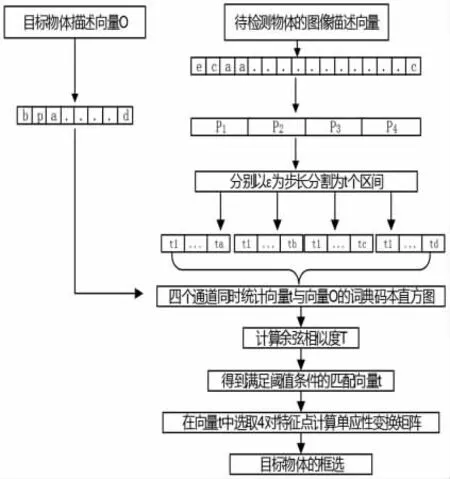
图6 匹配识别流程图Fig.6 Matching Recognition Flow Chart

4 实验结果与分析

4.1 实验条件

所有实验的测试平台为：VS2013 +OpenCV2.4.13 和MATLAB2014a，CPU 英特尔i5-6220U，2.30GHz；64 位Windows 10 操作系统的计算机。相机采集装置为大恒相机MER-1070/C拍摄的（3840×2748）分辨率的图像，并根据实际实验将图像处理到较低的分辨率。实验用的目标识别物体部分图像，如图7 所示。分选取了电机支架安装板、同步带轮、装配工具作为代表，从左到右依次命名为物体1、物体2、物体3。另外在进行算法参数选定实验时采用图像特征检测领域中常用的数据集Mikolajczyk 进行测试，包含8 组48 幅图像，包括了常见的图像旋转、尺度、视角、光照等变换以及复合变换。

同时在进行实际物体识别实验时将改进算法分别与SIFT算法、SURF 算法、H_SURF 算法进行物体识别效果对比，分别从识别准确率、识别所用时间两个方面进行衡量并说明方法的识别效果。

图7 待识别物体图Fig.7 Object Map to be Identified

4.2 采样步长ε 的确定

采样步长ε 影响待检测物体描述向量pi的划分数量、划分重叠度，进而影响到后续与目标物体向量的匹配速度。较大的采样步长会降低划分重叠度，减少划分子向量的数量，从而提高匹配速度；但是，较大的采样步长会使描述向量之间的差异性变大，减少了与目标物体描述向量具有较大相似度的概率，这样会使目标匹配的准确度下降。

在保证一定准确度的条件下，我们要提高算法匹配的效率就要选择合适的采样步长。实验采用Mikolajczyk 图像测试集中包含尺度、旋转、光照以及三种变换组合情况下的三组图像构造识别模板和测试图像。其中三组图像中选取的测试图像识别模板和测试集，如图8 所示。

图8 实验所用模板图像以及测试集图像Fig.8 Template Image and Test Set Image for Experiment

考虑实际应用中不同相机采集的图像大小尺寸不同，模板制作大小不同，在生成物体描述向量的维度也不相同。选取的采样步长应该以模板图像以及测试图像的大小比例来选取。实验所用采样步长ε 的取值分别为模板图像描述向量的1/16 到1/8。不同初始化采样步长的识别用时和识别的准确率，如图9 所示。图中数据为5 次测量取的平均值。

通过图9 可以看出，随着采样步长的增大，识别的准确率在下降同时所消耗的时间在减少，通过对比图9（a）和图9（b）我们可以发现，采样步长设置为1/10 时，识别所用时间有一个较大的下降，并且在该采样步长下，识别的准确率可以取得一个较高的水平。

图9 不同采样步长下的识别效果对比Fig.9 Comparison of Recognition Effects Under Different Sampling Steps

综合考虑准确率与消耗时间两方面的因素，最终选取采样步长取值为模板物体描述向量的十分之一。

4.3 滤波变换下描述向量识别区域对比

图10 相同滤波条件下检测效果对比Fig.10 Comparison of Detection Results Under the Same Filtering Condition

在相同滤波尺度下，改进的目标工件描述向量在相同光照、尺度等变换下具有更好的区分性，相比原SURF 算法更有利于后期目标物体的识别，两种算法在相同滤波参数下分别对三种目标物体描述效果对比，如图10 所示。

通过图10 中对比可以发现，在相同外界条件下，改进的描述向量相比原SURF 描述子对目标物体图像的描述有更加明显的外部轮廓。在能够准确的识别出物体图像的前提下减少了大量冗余特征和图像噪声[16]，这些特征可以减少算法的计算量，同时可以保证后期算法识别的准确性。

4.4 不同条件下目标物体识别效果对比

4.4.1 不同尺度下物体识别效果对比

根据物体尺度不同，每种物体利用相机采集3 组不同尺度下的图像，每组采集二十张，识别图像分辨率大小为（1280×916）。通过算法构建物体描述向量进行匹配，识别效果，如图11 所示。其中黄色矩形框为改进算法提出的物体描述向量所形成的描述区域范围。

图11 尺度变化下物体识别效果Fig.11 Object Recognition Effect Under Scale Change

在一定的尺度变换条件下，改进算法可以较好的实现目标物体的框选，同时改进算法提出的匹配模型可以准确的表示出目标物体的主要特征，如图11 所示。

此外计算每组物体识别所用平均时间，与SURF 算法识别物体进行比较分析，结果如表1 所示。并对算法的正确识别率进行计算，正确识别率为准确识别到目标物体的图像数量占总数量的比例，计算公式为式（5）。三种算法与改进算法的平均正确匹配率以及平均匹配时间的比较，如表1 所示。

表1 尺度变换下物体识别效果比较Tab.1 Comparison of Object Recognition Effect Under Scale Transformation

通过表1 中数据可以看出，在识别率保持和原算法接近的前提下，识别用时比原SURF 算法提高了约7.76%，同样可以看出H_SURF 算法在实时性上高于原SURF 算法，但在识别率上还略低于改进算法，识别正确率最高的为SIFT 算法，但是SIFT 算法用时最长，而且改进算法识别率已经能够达到准确识别物体，综合性能高于SIFT 算法。

4.4.2 不同光照下物体识别效果对比

根据物体光照不同，同样每种物体利用相机采集3 组不同光照下的图像，每组选取二十张，识别图像分辨率大小也为（1280×916）。改进算法识别效果，如图12 所示。其中黄色矩形框为提出的物体描述向量所描述的物体区域。

图12 光照变化下物体识别效果Fig.12 Object Recognition Effect Under Illumination Change

通过图12 可以看出在一定光照变换下，改进算法同样可以较准确的实现目标物体的框选，由于物体的形状、颜色等差异，在生成描述子的时候目标物体的表达范围有一定的差异。但是，目标物体的主要特征可以比较准确的提取出来，从而计算出准确的单应性变换矩阵，实现目标物体的框选。相同实验条件下四种算法的平均识别正确率以及算法平均耗时对比，如表2 所示。

表2 光照变换下物体识别效果比较Tab.2 Comparison of Object Recognition Effect Under Illumination Transformation

表2 中数据可以看出算法在物体2 和3 的正确匹配率略低于原SURF 算法，这由于物体在光照变化下物体2 反光现象比较严重检测到的特征点数量会有所减少，而物体3 在光照变换下生成的描述向量区域发生了一定的旋转，造成转换矩阵计算不准确，从而降低了识别率。但改进算法相比原算法在光照变换下识别平均用时提高了约3.74%，同时在光照变换下H_SURF 算法的识别效率降低较明显，这也说明了，光照的变换对其算法的稳定性影响较大。

4.4.3 不同旋转角度下物体识别效果对比

根据物体旋转角度不同，同样每种物体利用相机采集3 组不同光照下的图像，每组选取二十张，待识别图像分辨率大小为（1280×916）。改进算法识别效果，如图13 所示。其中，矩形框同样为提出的物体描述向量所描述的物体区域。

图13 旋转角变化下物体识别效果Fig.13 Object Recognition Effect Under Rotation Angle Change

通过图13 可以看出在一定旋转变换下，改进算法提出的匹配模型可以追随目标物体的旋转角度进行识别变换，可以实现目标物体的准确识别。不同旋转角度的条件下进行四种算法的识别实验结果的平均值对比，如表3 所示。

表3 旋转变换下物体识别效果比较Tab.3 Comparison of Object Recognition Effect Under Rotation Transformation

表3 中数据可以看出算法在旋转条件下具有优于原SURF算法的匹配率，改进的匹配模型利用的反向标记的方法对于旋转不变性具有更好的鲁棒性，同时识别时间比原SURF 算法约提高了3.33%；相比H_SURF 算法在识别准确性以及识别效率上都有一定的提高。说明改进算法在图像旋转变换下同样具有一定的实用性。

5 结论

针对基于SURF 特征的工件快速识别，提出一种改进的装配工件快速识别方法。算法在特征描述和匹配阶段主要有以下几个改进步骤；（1）通过K-means 方法对目标物体特征点种类进行分类，从而可以增强局部特征的可描述性和差异性；（2）利用特征点种类构造词袋模型，可以增强特征的可检索性，同时减少匹配时的搜索时间；（3）基于词袋模型生成目标物体的描述向量，并且利用描述向量进行物体匹配识别，减少了大量特征点之间欧氏距离的计算。实验结果表明，在尺度变换因子取原图的0.6 倍至1.8倍之间、光照变换因子区间取原图的（0.8～1.6）、旋转变换角度范围为（±60）°时，改进算法较原SURF 算法在保证识别准确率的基础上，识别速度整体提高了约4.94%。所用实验图像集在该光照变换区间内，改进算法的识别准确率相比H_SURF 算法提高了接近9%，并且具有更加稳定的识别效果。但是，基于词袋模型的物体描述向量对于图像中工件局部区域性特征的区分性还有一定的不足，这是提高工件识别准确率的关键，也是以后研究的方向。